C++性能優(yōu)化
性能優(yōu)化不管是從方法論還是從實(shí)踐上都有很多東西,從 C++ 語言本身入手,介紹一些性能優(yōu)化的方法,希望能做到簡(jiǎn)潔實(shí)用。
實(shí)例1
在開始本文的內(nèi)容之前,讓我們看段小程序:
// 獲取一個(gè)整數(shù)對(duì)應(yīng)10近制的位數(shù)
uint32_t digits10_v1(uint64_t v) {
uint32_t result = 0;
do {
++result;
v /= 10;
} while (v);
return result;
}
如果要對(duì)這段代碼進(jìn)行優(yōu)化,你認(rèn)為瓶頸會(huì)是什么呢?代碼 -g -O2 后看一眼匯編:
Dump of assembler code for function digits10_v1(uint64_t):
0x00000000004008f0 <digits10_v1(uint64_t)+0>: mov %rdi,%rdx
0x00000000004008f3 <digits10_v1(uint64_t)+3>: xor %esi,%esi
0x00000000004008f5 <digits10_v1(uint64_t)+5>: mov $0xcccccccccccccccd,%rcx
0x00000000004008ff <digits10_v1(uint64_t)+15>: nop
0x0000000000400900 <digits10_v1(uint64_t)+16>: mov %rdx,%rax
0x0000000000400903 <digits10_v1(uint64_t)+19>: add $0x1,%esi
0x0000000000400906 <digits10_v1(uint64_t)+22>: mul %rcx
0x0000000000400909 <digits10_v1(uint64_t)+25>: shr $0x3,%rdx
0x000000000040090d <digits10_v1(uint64_t)+29>: test %rdx,%rdx
0x0000000000400910 <digits10_v1(uint64_t)+32>: jne 0x400900 <digits10_v1(uint64_t)+16>
0x0000000000400912 <digits10_v1(uint64_t)+34>: mov %esi,%eax
0x0000000000400914 <digits10_v1(uint64_t)+36>: retq
/*
注:對(duì)于常數(shù)的除法操作,編譯器一般會(huì)轉(zhuǎn)換成乘法+移位的方式,即
a / b = a * (1/b) = a * (2^n / b) * (1 / 2^n) = a * (2^n / b) >> n.
這里的n=3, b=10, 2^n/b=4/5,0xcccccccccccccccd是編譯器對(duì)4/5的定點(diǎn)算法表示
*/
指令已經(jīng)很少了,有多少優(yōu)化空間呢?先不著急,看看下面這段代碼
uint32_t digits10_v2(uint64_t v) {
uint32_t result = 1;
for (;;) {
if (v < 10) return result;
if (v < 100) return result + 1;
if (v < 1000) return result + 2;
if (v < 10000) return result + 3;
// Skip ahead by 4 orders of magnitude
v /= 10000U;
result += 4;
}
}
uint32_t digits10_v3(uint64_t v) {
if (v < 10) return 1;
if (v < 100) return 2;
if (v < 1000) return 3;
if (v < 1000000000000) { // 10^12
if (v < 100000000) { // 10^7
if (v < 1000000) { // 10^6
if (v < 10000) return 4;
return 5 + (v >= 100000); // 10^5
}
return 7 + (v >= 10000000); // 10^7
}
if (v < 10000000000) { // 10^10
return 9 + (v >= 1000000000); // 10^9
}
return 11 + (v >= 100000000000); // 10^11
}
return 12 + digits10_v3(v / 1000000000000); // 10^12
}
寫了一個(gè)小程序,digits10_v2 比 digits10_v1 快了 45%, digits10_v3 比digits10_v1 快了60%+。不難看出測(cè)試結(jié)論跟數(shù)據(jù)的取值范圍相關(guān),就本例來說數(shù)值越大,提升越明顯。是什么原因呢?附測(cè)試程序:
int main() {
srand(100);
uint64_t digit10_array[ITEM_COUNT];
for( int i = 0; i < ITEM_COUNT; ++i )
{
digit10_array[i] = rand();
}
struct timeval start, end;
// digits10_v1
uint64_t sum1 = 0;
uint64_t time1 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum1 += digits10_v1(digit10_array[i]);
}
gettimeofday(&end,NULL);
time1 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v2
uint64_t sum2 = 0;
uint64_t time2 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum2 += digits10_v2(digit10_array[i]);
}
gettimeofday(&end,NULL);
time2 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v3
uint64_t sum3 = 0;
uint64_t time3 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum3 += digits10_v3(digit10_array[i]);
}
gettimeofday(&end,NULL);
time3 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
cout << "sum1:" << sum1 << "\t sum2:" << sum2 << "\t sum3:" << sum3 << endl;
cout << "cost1:" << time1 << "us\t cost2:" << time2 << "us\t cost3:" << time3 << "us"
<< "\t cost2/cost1:" << (1.0*time2)/time1
<< "\t cost3/cost1:" << (1.0*time3)/time1 << endl;
return 0;
}
/*
執(zhí)行結(jié)果:
g++ -g -O2 cplusplus_optimize.cpp && ./a.out
sum1:9944152 sum2:9944152 sum3:9944152
cost1:27560us cost2:14998us cost3:10525us cost2/cost1:0.544194 cost3/cost1:0.381894
*/
Strength reduction
優(yōu)化原因不是因?yàn)樽隽搜h(huán)展開,而是由于不同指令本身的速度就是不一樣的,比較、整型的加減、位操作速度都是最快的,而除法/取余卻很慢。下面有一個(gè)更詳細(xì)的列表,為了更直觀一些,用了clock cycle 來衡量,不過這里的 clock cycle 是個(gè)平均值,不同的 CPU 還是稍有差異:
* comparisons (1 clock cycle)
* (u)int add, subtract, bitops, shift (1 clock cycle)
* floating point add, sub (3~6 clock cycle)
* indexed array access (cache effects)
* (u)int32 mul (3~4 clock cycle)
* Floating point mul (4~8 clock cycle)
* Float Point division, remainder (14~45 clock cycle)
* (u)int division, remainder (40~80 clock cycle)
雖然大多數(shù)場(chǎng)景下,數(shù)學(xué)運(yùn)算都不會(huì)有太多性能問題,但相對(duì)來說,整型的除法運(yùn)算還是比較昂貴的。編譯器就會(huì)利用這一特點(diǎn)進(jìn)行優(yōu)化,一般稱作 Strength reduction.
對(duì)于前面的例子,核心原因是 digits10_v2 用比較和加法來減少除法 (/=) 操作,digits10_v3 通過搜索的方式進(jìn)一步減少了除法操作。由于 cpu 并行處理技術(shù),我們不能簡(jiǎn)單的用后面的 clock cycle 來衡量性能,但不難看出處理器對(duì)類型的還是非常敏感的,以整型和浮點(diǎn)的處理為例:
整型
類型轉(zhuǎn)換
int--> short/char (0~1 clock cycle) int --> float/double (4~16個(gè)clock cycle), signed int 快于 unsigned int,唯一一個(gè)場(chǎng)景 signed 比 unsigned 快的 short/char 的計(jì)算通常使用 32bit 存儲(chǔ),只是返回的時(shí)候做了截取,故只在要考慮內(nèi)存大小的時(shí)候才使用 short/char,如 array 注:隱式類型轉(zhuǎn)換可能會(huì)溢出,有符號(hào)的溢出變成負(fù)數(shù),無符號(hào)的溢出變成小的整數(shù)
運(yùn)算
除法、取余運(yùn)算unsigned int 快于 signed int 除以常量比除以變量效率高,因?yàn)榭梢栽诰幾g期做優(yōu)化,尤其是常量可以表示成2^n時(shí) ++i和i++本身性能一樣,但不同的語境效果不一樣,如array[i++]比arry[++i]性能好;當(dāng)依賴自增結(jié)果時(shí),++i性能更好,如a=++b,a和b可復(fù)用同一個(gè)寄存器
代碼示例
// div和mod效率
int a, b, c;
a = b / c; // This is slow
a = b / 10; // Division by a constant is faster
a = (unsigned int)b / 10; // Still faster if unsigned
a = b / 16; // Faster if divisor is a power of 2
a = (unsigned int)b / 16; // Still faster if unsigned
浮點(diǎn)
單精度、雙精度的計(jì)算性能是一樣的 常量的默認(rèn)精度是雙精度 不要混淆單精度、雙精度,混合精度計(jì)算會(huì)帶來額外的精度轉(zhuǎn)換開銷,如
// 混用
float a, b;
a = b * 1.2; // bad. 先將b轉(zhuǎn)換成double,返回結(jié)果轉(zhuǎn)回成float
// Example 14.18b
float a, b;
a = b * 1.2f; // ok. everything is float
// Example 14.18c
double a, b;
a = b * 1.2; // ok. everything is double
浮點(diǎn)除法比乘法慢很多,故可以利用乘法來加快速度,如:
double y, a1, a2, b1, b2;
y = a1/b1 + a2/b2; // slow
double y, a1, a2, b1, b2;
y = (a1*b2 + a2*b1) / (b1*b2); // faster
這里介紹的大多是編譯器的擅長(zhǎng)但又不能直接優(yōu)化的場(chǎng)景,也是平常優(yōu)化中比較容易忽視的點(diǎn),其實(shí)往往我們往前多走一步,編譯器就可以工作得更好。
實(shí)例2
先看一個(gè)數(shù)字轉(zhuǎn)字符串的例子,stringstream 和 sprintf 自然不會(huì)是我們考慮的對(duì)象,雖然 protobuf 庫中的 FastInt32ToBuffer 很不錯(cuò),其實(shí)還能優(yōu)化,下面的版本就比例子中 stringstream 快 6 倍,代碼如下:
// integer to string
uint32_t u64ToAscii_v1(uint64_t value, char* dst) {
// Write backwards.
char* start = dst;
do {
*dst++ = '0' + (value % 10);
value /= 10;
} while (value != 0);
const uint32_t result = dst - start;
// Reverse in place.
for (dst--; dst > start; start++, dst--) {
std::iter_swap(dst, start);
}
return result;
}
不用細(xì)讀 stringstream/sprintf 的源碼,反匯編看下就能知道個(gè)大概,對(duì)于轉(zhuǎn)字符串這個(gè)場(chǎng)景,stringstream/sprintf 就太重了,通常來說越少的指令性能也越好,本文討論的重點(diǎn)是內(nèi)存訪問,就上面這段代碼,有什么內(nèi)存使用上的問題?如何進(jìn)一步優(yōu)化?
分析
優(yōu)化前還是得找一下性能熱點(diǎn),下面是 vtune 結(jié)果的截圖(雖然 cpu time 和匯編指令的消耗對(duì)應(yīng)得不是特別好):
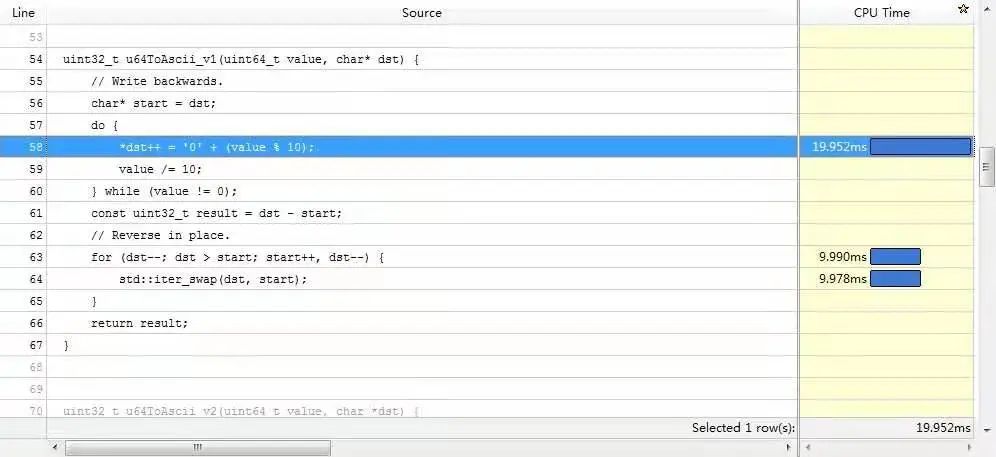
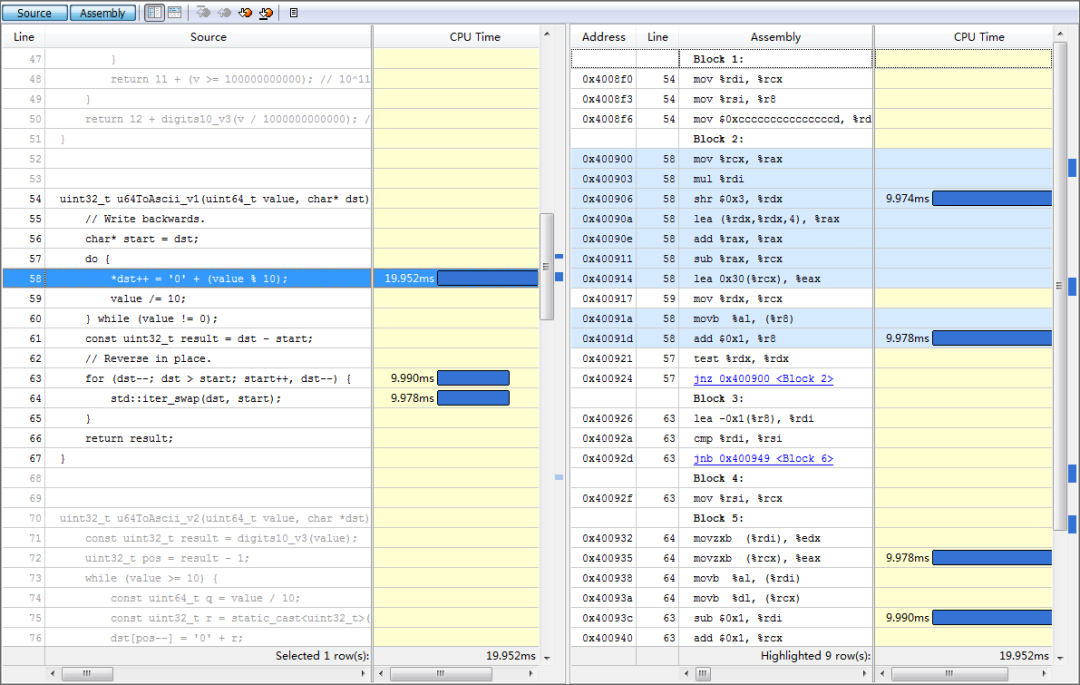
數(shù)組 reverse 的開銷跟上面生成數(shù)組元素相近,reverse有這么耗時(shí)么?
從圖中的匯編可以看出,一次 swap 對(duì)應(yīng)著兩次內(nèi)存讀 (movzxb)、兩次內(nèi)存寫 (movb),因?yàn)橐淮螌懢鸵馕吨粋€(gè)讀和一個(gè)寫,描述的是內(nèi)存-->cache-->內(nèi)存的過程。
優(yōu)化
減少內(nèi)存寫操作一個(gè)很自然的優(yōu)化想法,應(yīng)該盡量避免內(nèi)存寫操作,于是代碼可以進(jìn)一步優(yōu)化,結(jié)合 Strength reduction,代碼如下:
uint32_t u64ToAscii_v2(uint64_t value, char *dst) {
const uint32_t result = digits10_v3(value);
uint32_t pos = result - 1;
while (value >= 10) {
const uint64_t q = value / 10;
const uint32_t r = static_cast<uint32_t>(value % 10);
dst[pos--] = '0' + r;
value = q;
}
*dst = static_cast<uint32_t>(value) + '0';
return result;
}
實(shí)測(cè)發(fā)現(xiàn)新版本比之前版本性能提升了 10%,還有優(yōu)化空間么?答案是,有。方案是:通過查表,一次處理2個(gè)數(shù)字,減少數(shù)據(jù)依賴,如:
uint32_t u64ToAscii_v3(uint64_t value, char* dst) {
static const char digits[] =
"0001020304050607080910111213141516171819"
"2021222324252627282930313233343536373839"
"4041424344454647484950515253545556575859"
"6061626364656667686970717273747576777879"
"8081828384858687888990919293949596979899";
const size_t length = digits10_v3(value);
uint32_t next = length - 1;
while (value >= 100) {
const uint32_t i = (value % 100) * 2;
value /= 100;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
next -= 2;
}
// Handle last 1-2 digits
if (value < 10) {
dst[next] = '0' + uint32_t(value);
} else {
uint32_t i = uint32_t(value) * 2;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
}
return length;
}
結(jié)論:
u64ToAscii_v3性能比基準(zhǔn)版本提升了30%; 如果用到悟時(shí)的那個(gè)測(cè)試場(chǎng)景,性能可以提升6.5倍。
下面是完整的測(cè)試代碼和結(jié)果:
#include <sys/time.h>
#include <iostream>
#define ITEM_COUNT 1024*1024
#define RUN_TIMES 1024*1024
#define BUFFERSIZE 32
using namespace std;
uint32_t digits10_v1(uint64_t v) {
uint32_t result = 0;
do {
++result;
v /= 10;
} while (v);
return result;
}
uint32_t digits10_v2(uint64_t v) {
uint32_t result = 1;
for(;;) {
if (v < 10) return result;
if (v < 100) return result + 1;
if (v < 1000) return result + 2;
if (v < 10000) return result + 3;
v /= 10000U;
result += 4;
}
return result;
}
uint32_t digits10_v3(uint64_t v) {
if (v < 10) return 1;
if (v < 100) return 2;
if (v < 1000) return 3;
if (v < 1000000000000) { // 10^12
if (v < 100000000) { // 10^7
if (v < 1000000) { // 10^6
if (v < 10000) return 4;
return 5 + (v >= 100000); // 10^5
}
return 7 + (v >= 10000000); // 10^7
}
if (v < 10000000000) { // 10^10
return 9 + (v >= 1000000000); // 10^9
}
return 11 + (v >= 100000000000); // 10^11
}
return 12 + digits10_v3(v / 1000000000000); // 10^12
}
uint32_t u64ToAscii_v1(uint64_t value, char* dst) {
// Write backwards.
char* start = dst;
do {
*dst++ = '0' + (value % 10);
value /= 10;
} while (value != 0);
const uint32_t result = dst - start;
// Reverse in place.
for (dst--; dst > start; start++, dst--) {
std::iter_swap(dst, start);
}
return result;
}
uint32_t u64ToAscii_v2(uint64_t value, char *dst) {
const uint32_t result = digits10_v3(value);
uint32_t pos = result - 1;
while (value >= 10) {
const uint64_t q = value / 10;
const uint32_t r = static_cast<uint32_t>(value % 10);
dst[pos--] = '0' + r;
value = q;
}
*dst = static_cast<uint32_t>(value) + '0';
return result;
}
uint32_t u64ToAscii_v3(uint64_t value, char* dst) {
static const char digits[] =
"0001020304050607080910111213141516171819"
"2021222324252627282930313233343536373839"
"4041424344454647484950515253545556575859"
"6061626364656667686970717273747576777879"
"8081828384858687888990919293949596979899";
const size_t length = digits10_v3(value);
uint32_t next = length - 1;
while (value >= 100) {
const uint32_t i = (value % 100) * 2;
value /= 100;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
next -= 2;
}
// Handle last 1-2 digits
if (value < 10) {
dst[next] = '0' + uint32_t(value);
} else {
uint32_t i = uint32_t(value) * 2;
dst[next - 1] = digits[i];
dst[next] = digits[i + 1];
}
return length;
}
int main() {
srand(100);
uint64_t digit10_array[ITEM_COUNT];
for( int i = 0; i < ITEM_COUNT; ++i )
{
digit10_array[i] = rand();
}
char buffer[BUFFERSIZE];
struct timeval start, end;
// digits10_v1
uint64_t sum1 = 0;
uint64_t time1 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum1 += u64ToAscii_v1(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time1 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v2
uint64_t sum2 = 0;
uint64_t time2 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum2 += u64ToAscii_v2(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time2 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
// digits10_v3
uint64_t sum3 = 0;
uint64_t time3 = 0;
gettimeofday(&start,NULL);
for( int i = 0; i < RUN_TIMES; ++i )
{
sum3 += u64ToAscii_v3(digit10_array[i], buffer);
}
gettimeofday(&end,NULL);
time3 = ( end.tv_sec - start.tv_sec ) * 1000 * 1000 + end.tv_usec - start.tv_usec;
cout << "sum1:" << sum1 << "\t sum2:" << sum2 << "\t sum3:" << sum3 << endl;
cout << "cost1:" << time1 << "us\t cost2:" << time2 << "us\t cost3:" << time3 << "us"
<< "\t cost2/cost1:" << (1.0*time2)/time1
<< "\t cost3/cost1:" << (1.0*time3)/time1 << endl;
return 0;
}
/* 測(cè)試結(jié)果
g++ -g -O2 cplusplus_optimize.cpp -o cplusplus_optimize && ./cplusplus_optimize
sum1:9944152 sum2:9944152 sum3:9944152
cost1:47305us cost2:42448us cost3:31657us cost2/cost1:0.897326 cost3/cost1:0.66921
*/
看到優(yōu)化寫內(nèi)存操作的威力了吧,讓我們?cè)倏匆粋€(gè)減少寫操作的例子:
struct Bitfield {
int a:4;
int b:2;
int c:2;
};
Bitfield x;
int A, B, C;
x.a = A;
x.b = B;
x.c = C;
假定 A、B、C 都很小,且不會(huì)溢出,可以寫成
union Bitfield {
struct {
int a:4;
int b:2;
int c:2;
};
char abc;
};
Bitfield x;
int A, B, C;
x.abc = A | (B << 4) | (C << 6);
如果需要考慮溢出,也可以改為
x.abc = (A & 0x0F) | ((B & 3) << 4) | ((C & 3) <<6 );
讀取效率
對(duì)于內(nèi)存的寫,最好的辦法就是減少寫的次數(shù),那么內(nèi)存的讀取呢?教科書的答案是:盡可能順序訪問內(nèi)存。理解這句話還是得從 cache line 開始,因?yàn)閷?shí)際的 cpu 比較復(fù)雜,下面的表述嘗試做些簡(jiǎn)化,如有問題,歡迎指正:
cache line
假設(shè) L1cache 大小為 8K,cache line 64 字節(jié)、4way,那么整個(gè) cache 會(huì)分成32 個(gè)集合,81024/64=128=324,一個(gè)內(nèi)存地址進(jìn)入哪個(gè) cache line 不是任意的,而是確定在某個(gè)集合中,可以通過公式 (set ) = (memory address) / ( line size) % (number of sets )來計(jì)算,如地址是 10000,則(set)=10000/64%32 = 28, 即編號(hào)為28的集合內(nèi)的4個(gè) cache line 之一。用 16 進(jìn)制來描述,10000=0x2710 ,一次內(nèi)存讀取是 64bytes,那么訪問內(nèi)存地址 10000 即意味著地址 0x2700~0x273F 都進(jìn)集合編號(hào)為 28(0x1C) 的 cache line 中了。
cache miss
可以看出,順序的訪問內(nèi)存是能夠比較高效而且不會(huì)因?yàn)?cache 沖突,導(dǎo)致藥頻繁讀取內(nèi)存。那什么的情況會(huì)導(dǎo)致 cache miss 呢?
當(dāng)某個(gè)集合內(nèi)的 cache line 都有數(shù)據(jù)時(shí),且該集合內(nèi)有新的數(shù)據(jù)就會(huì)導(dǎo)致老數(shù)據(jù)的換出,進(jìn)而訪問老數(shù)據(jù)就會(huì)出現(xiàn) cache miss。 以先后讀取 0x2710, 0x2F00, 0x3700, 0x3F00, 0x4700 為例, 這幾個(gè)地址都在 28 這個(gè)編號(hào)的集合內(nèi),當(dāng)去讀 0x4700 時(shí),假定 CPU 都是以先進(jìn)先出策略,那么 0x2710 就會(huì)被換出,這時(shí)候如果再訪問 0x2700~0x273F 的數(shù)據(jù)就 cache miss,需要重新訪問內(nèi)存了。 可以看出變量是否有 cache 競(jìng)爭(zhēng),得看變量地址間的距離, distance = (number of sets ) (line size) = ( total cache size) / ( number of ways), 即距離為3264 = 8K/4= 2K的內(nèi)存訪問都可能產(chǎn)生競(jìng)爭(zhēng)。上面這些不光對(duì)變量、對(duì)象有用,對(duì)代碼 cache 也是如此。
建議
對(duì)于內(nèi)存的訪問,可以考慮以下一些建議:
一起使用的函數(shù)存儲(chǔ)在一起。函數(shù)的存儲(chǔ)通常按照源碼中的順序來的,如果函數(shù)A,B,C是一起調(diào)用的,那盡量讓ABC的聲明也是這個(gè)順序 一起使用的變量存儲(chǔ)在一起。使用結(jié)構(gòu)體、對(duì)象來定義變量,并通過局部變量方式來聲明,都是一些較好的選擇。例子見后文: 合理使用對(duì)齊(attribute((aligned(64)))、預(yù)取(prefecting data),讓一個(gè)cacheline能獲取到更多有效的數(shù)據(jù) 動(dòng)態(tài)內(nèi)存分配、STL容器、string都是一些常容易cache不友好的場(chǎng)景,核心代碼處盡量不用
int Func(int);
const int size = 1024;
int a[size], b[size], i;
...
for (i = 0; i < size; i++) {
b[i] = Func(a[i]);
}
// pack a,b to Sab
int Func(int);
const int size = 1024;
struct Sab {int a; int b;};
Sab ab[size];
int i;
...
for (i = 0; i < size; i++) {
ab[i].b = Func(ab[i].a);
}
靜態(tài)變量
讓我們?cè)倩氐阶钋懊娴膬?yōu)化,u64ToAscii_v3 引入了局部靜態(tài)變量 (digits),是否合適?通常來說,要具體問題具體分析,沒有標(biāo)準(zhǔn)答案。
靜態(tài)變量和棧地址是分開的,可能會(huì)帶來 cache miss 的問題,通過去掉 static 修飾符,直接在棧上聲明變的方式可以避免,但這種做法可行有幾個(gè)前提條件:
變量大小是要限制的,不超出cache的大小(最好是L1 cache) 變量的初始化在棧上完成,故最好不要在循環(huán)內(nèi)部定義,以避免不必要的初始化。
其實(shí)內(nèi)存訪問和 CPU 運(yùn)算是沒有一定的贏家,真正做優(yōu)化時(shí),需要結(jié)合具體的場(chǎng)景,仔細(xì)測(cè)量才能得到答案。
回顧
前面兩個(gè)實(shí)例分別從編譯器和內(nèi)存使用的角度介紹了一些性能優(yōu)化的方法,后面內(nèi)容則會(huì)回到cpu,從指令并行的角度看看我們常見的邏輯控制有哪些可以優(yōu)化的點(diǎn)。
從原理上來說,這個(gè)系列的優(yōu)化不是特別區(qū)分語言,只是這里我們用C++來描述。
流水線
通常一個(gè) CPU 可以并行執(zhí)行多條指令,如:4 條浮點(diǎn)乘法,等待 4 個(gè)內(nèi)存訪問、一個(gè)還為到來的分支比較,不同的運(yùn)算單元也是可以并行計(jì)算,如 for(int i = 0; i < N; ++i) a[i]=0.2; 這里的 i < N 和 ++i 在 a[i]=0.2 可以同時(shí)執(zhí)行。提升指令并行能力,往往就能達(dá)到提升性能的目的。
從流水線的角度看,指令 pipeline 的幾個(gè)階段:fetch、decode、execute、memory-access、write-back,除了存儲(chǔ)器的訪問效率會(huì)影響并行度外,下一條指令的 fetch/decode 也很關(guān)鍵,而跳轉(zhuǎn)和分支則是又一個(gè)攔路虎,這也是本文接下去要主要分析的地方。
函數(shù)
本身開銷
函數(shù)調(diào)用使得處理器跳到另外一個(gè)代碼地址并回來,一般需要4 clock cycles,大多數(shù)情況處理器會(huì)把函數(shù)調(diào)用、返回和其他指令一起執(zhí)行以節(jié)約時(shí)間。 函數(shù)參數(shù)存儲(chǔ)在棧上需要額外的時(shí)間( 包括棧幀的建立、saving and restoring registers、可能還有異常信息)。在64bit linux上,前6個(gè)整型參數(shù)(包括指針、引用)、前8個(gè)浮點(diǎn)參數(shù)會(huì)放到寄存器中;64bit windows上不管整型、浮點(diǎn),會(huì)放置4個(gè)參數(shù)。 在內(nèi)存中過于分散的代碼可能會(huì)導(dǎo)致較差的code cache
常見的優(yōu)化手段
避免不必要的函數(shù),特別在最底層的循環(huán),應(yīng)該盡量讓代碼在一個(gè)函數(shù)內(nèi)。看起來與良好的編碼習(xí)慣沖突(一個(gè)函數(shù)最好不要超過80行),其實(shí)不然,跟這個(gè)系列其他優(yōu)化一樣,我們應(yīng)該知道何時(shí)去使用這些優(yōu)化,而不是一上來就讓代碼不可讀。 嘗試使用inline函數(shù),讓函數(shù)調(diào)用的地方直接用函數(shù)體替換。inline對(duì)編譯器來說是個(gè)建議,而且不是inline了性能就好,一般當(dāng)函數(shù)比較小或者只有一個(gè)地方調(diào)用的時(shí)候,inline效果會(huì)比較好 在函數(shù)內(nèi)部使用循環(huán)(e.g., change for(i=0;i<100;i++) DoSomething(); into DoSomething(){ for(i=0;i<100;i++) { ... } } ) 減少函數(shù)的間接調(diào)用,如偏向靜態(tài)鏈接而不是動(dòng)態(tài)鏈接,盡量少用或者不用多繼承、虛擬繼承 優(yōu)先使用迭代而不是遞歸 使用函數(shù)來替換define,從而避免多次求值。宏的其他缺點(diǎn):不能overload和限制作用域(undef除外)
// Use macro as inline function
#define MAX(a,b) ((a) > (b) ? (a) : (b))
y = MAX(f(x), g(x));
// Replace macro by template
template <typename T>
static inline T max(T const & a, T const & b) {
return a > b ? a : b;
}
分支預(yù)測(cè)
應(yīng)用場(chǎng)景
常見的分支預(yù)測(cè)場(chǎng)景有 if/else,for/while,switch,預(yù)測(cè)正確 0~2 clock cycles,錯(cuò)誤恢復(fù) 12~25 clock cycles。
一般應(yīng)用分支預(yù)測(cè)的正確率在90%以上,但個(gè)位數(shù)的誤判率對(duì)有較多分支的程序來說影響還是非常大的。分支預(yù)測(cè)的技術(shù)(或者說策略)非常多,這里不會(huì)展開介紹,對(duì)寫程序來說,我們知道越簡(jiǎn)單的場(chǎng)景越容易預(yù)測(cè)正確:如分支都在在一個(gè)循環(huán)內(nèi)或者幾乎沒有其他分支。
關(guān)鍵因素
如果對(duì)分支預(yù)測(cè)的概念和作用還不清楚的話,可以看看后面的參考文檔。幾個(gè)影響分支預(yù)測(cè)因素:
branch target buffer (BTB)
分支預(yù)測(cè)的結(jié)果存儲(chǔ)一個(gè)特殊的cache,該cache是個(gè)固定大小的hashtable,通過$pc可以計(jì)算出預(yù)測(cè)結(jié)果地址 在指令fetch階段訪問,使得分支目標(biāo)地址在IF階段就可以讀取.預(yù)測(cè)不正確時(shí)更新預(yù)測(cè)結(jié)果
Return Address Stack (RAS)
固定大小,操作方式跟stack結(jié)構(gòu)一樣,內(nèi)容是函數(shù)返回值地址($pc+4), 使用BTB存儲(chǔ) 間接的跳轉(zhuǎn)不便于預(yù)測(cè),如依賴寄存器、內(nèi)存地址,好在絕大多數(shù)間接的跳轉(zhuǎn)都來自函數(shù)返回 函數(shù)返回地址預(yù)測(cè)使用BTB,如果關(guān)鍵部分的函數(shù)和分支較多,會(huì)引起B(yǎng)TB的競(jìng)爭(zhēng),進(jìn)而影響分支命中率
常見的優(yōu)化手段
1. 消除條件分支
代碼實(shí)例
if (a < b) {
r = c;
} else {
r = d;
}
優(yōu)化版本1
int mask = (a-b) >> 31;
r = (mask & c) | (~mask & d);
優(yōu)化版本2
int mask = (a-b) >> 31;
r = d + mask & (c-d);
優(yōu)化版本3
// cmovg版本
r = (a < b) ?c : d;
bool 類型變換
實(shí)例代碼
bool a, b, c, d;
c = a && b;
d = a || b;
編譯器的行為是
bool a, b, c, d;
if (a != 0) {
if (b != 0) {
c = 1;
}
else {
goto CFALSE;
}
}
else {
CFALSE:
c = 0;
}
if (a == 0) {
if (b == 0) {
d = 0;
}
else {
goto DTRUE;
}
}
else {
DTRUE:
d = 1;
}
優(yōu)化版本
char a = 0, b = 0, c, d;
c = a & b;
d = a | b;
實(shí)例代碼2
bool a, b;
b = !a;
// 優(yōu)化成
char a = 0, b;
b = a ^ 1;
反例
a && b 何時(shí)不能轉(zhuǎn)換成 a & b,當(dāng) a 不可能為 false 的情況下
a | | b 何時(shí)不能轉(zhuǎn)換成 a | b,當(dāng) a 不可能為 true 的情況下
2. 循環(huán)展開
實(shí)例代碼
int i;
for (i = 0; i < 20; i++) {
if (i % 2 == 0) {
FuncA(i);
}
else {
FuncB(i);
}
FuncC(i);
}
優(yōu)化版本
int i;
for (i = 0; i < 20; i += 2) {
FuncA(i);
FuncC(i);
FuncB(i+1);
Func
C(i+1);}
優(yōu)化說明
優(yōu)點(diǎn):減少比較次數(shù)、某些CPU上重復(fù)次數(shù)越少預(yù)測(cè)越準(zhǔn)、去掉了if判斷
缺點(diǎn):需要更多的code cache or micro-op cache、有些處理器(core 2)對(duì)于小循環(huán)性能很好(小于65bytes code)、循環(huán)的次數(shù)和展開的個(gè)數(shù)不匹配
一般編譯器會(huì)自動(dòng)展開循環(huán),程序員不需要主動(dòng)去做,除非有一些明顯優(yōu)點(diǎn),比如減少上面的if判斷
3. 邊界檢查
實(shí)例代碼1
const int size = 16; int i;
float list[size];
...
if (i < 0 || i >= size) {
cout << "Error: Index out of range";
}
else {
list[i] += 1.0f;
}
// 優(yōu)化版本
if ((unsigned int)i >= (unsigned int)size) {
cout << "Error: Index out of range";
}else {
list[i] += 1.0f;
}
實(shí)例代碼2
const int min = 100, max = 110; int i;
...
if (i >= min && i <= max) { ...
//優(yōu)化版本
if ((unsigned int)(i - min) <= (unsigned int)(max - min)) { ...
4. 使用數(shù)組
實(shí)例代碼1
float a; int b;
a = (b == 0) ? 1.0f : 2.5f;
// 使用靜態(tài)數(shù)組
float a; int b;
static const float OneOrTwo5[2] = {1.0f, 2.5f};
a = OneOrTwo5[b & 1];
實(shí)例代碼2
// 數(shù)組的長(zhǎng)度是2的冪
float list[16]; int i;
...
list[i & 15] += 1.0f;
5. 整形的 bit array 語義,適用于 enum、const、define
enum Weekdays {
Sunday, Monday, Tuesday, Wednesday, Thursday, Friday, Saturday
};
Weekdays Day;
if (Day == Tuesday || Day == Wednesday || Day == Friday) {
DoThisThreeTimesAWeek();
}
// 優(yōu)化版本 using &
enum Weekdays {
Sunday = 1, Monday = 2, Tuesday = 4, Wednesday = 8,
Thursday = 0x10, Friday = 0x20, Saturday = 0x40
};
Weekdays Day;
if (Day & (Tuesday | Wednesday | Friday)) {
DoThisThreeTimesAWeek();
}
本塊小結(jié)
盡可能的減少跳轉(zhuǎn)和分支 優(yōu)先使用迭代而不是遞歸 對(duì)于長(zhǎng)的if...else,使用switch case,以減少后面條件的判斷,把最容易出現(xiàn)的條件放在最前面 為小函數(shù)使用inline,減少函數(shù)調(diào)用開銷 在函數(shù)內(nèi)使用循環(huán) 在跳轉(zhuǎn)之間的代碼盡量減少數(shù)據(jù)依賴 嘗試展開循環(huán) 嘗試通過計(jì)算來消除分支
參考文檔
<<深入理解計(jì)算機(jī)系統(tǒng)>> http://en.wikipedia.org/wiki/Instruction_pipelining http://web.cecs.pdx.edu/~alaa/ece587/notes/bpred-6up.pdf http://cseweb.ucsd.edu/~j2lau/cs141/week8.html http://en.wikipedia.org/wiki/Branch_predictor http://en.wikipedia.org/wiki/Branch_target_predictor http://www-ee.eng.hawaii.edu/~tep/EE461/Notes/ILP/buffer.html http://book.51cto.com/art/200804/70903.htm http://en.wikipedia.org/wiki/Strength_reduction https://www.facebook.com/notes/facebook-engineering/three-optimization-tips-for-c/10151361643253920 http://people.cs.clemson.edu/~dhouse/courses/405/papers/optimize.pdf http://www.agner.org/optimize/optimizing_cpp.pdf
來源:https://developer.aliyun.com/article/412574?utm_source=wechat_session&utm_medium=social&utm_oi=887018450961186816
