用簡單的代碼,看懂 CPU 背后的重要機制
今天,stackoverflow 突然給我推送來一個問題。
我一看這個問題,竟然是 2012 年,也就是 8 年前的老問題。而其中的高票答案,都已經(jīng)有 30000 多個贊了。
仔細一看,這個問題還真挺有意思。
這個問題針對如下這樣一個簡單的代碼:

相信大家都能看懂。這段代碼對 data?數(shù)組中所有大于等于 128 的值進行求和。這樣的求和操作運行了 10 萬輪。
下面,我們來看一下這段代碼的性能。我們這樣隨機生成一個數(shù)組:
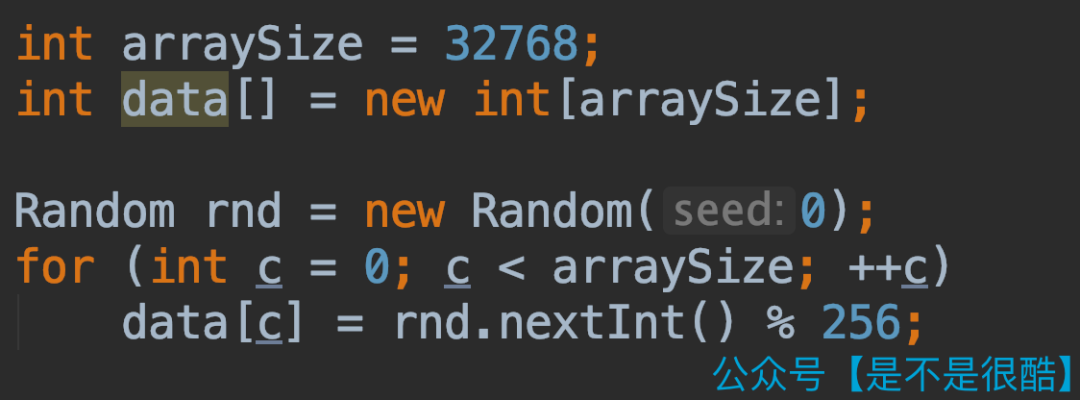
使用這個隨機生成的數(shù)組,測試上面的代碼。在我的計算機上,整體耗時是 8.5 秒左右。
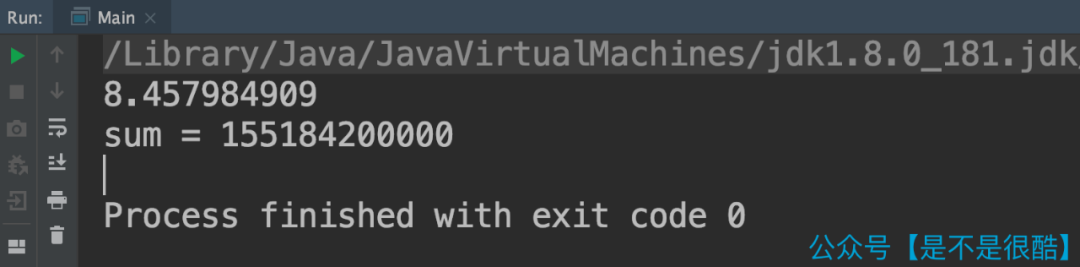
下面問題來了。如果,我對這個隨機的數(shù)組進行一遍排序。對排序后的數(shù)組執(zhí)行上面的代碼,性能會有怎樣的影響?
可能很多同學(xué)都會認為,性能是差不多的。
這是因為,上面的代碼過程,只是從頭到尾掃描數(shù)組,對于數(shù)組中的每一個元素,判斷其是否大于等于 128,如果是,就加入到 sum 中。
整個算法邏輯,和數(shù)組是否有序無關(guān)。有序的數(shù)組不會提前終止任何操作。不管是有序的數(shù)組,還是無序的數(shù)組,執(zhí)行的操作數(shù)量是一樣多的。
甚至,為了保持公平,我為隨機數(shù)生成器添加了種子。所以,兩次測試的數(shù)組中,大于等于 128 的元素個數(shù)都是一樣的。這就意味著 sum += data[c];?這個指令的執(zhí)行次數(shù)是一致的。
區(qū)別只有:第二次執(zhí)行,我先對數(shù)組進行了排序!
可是,實際結(jié)果卻是這樣的:
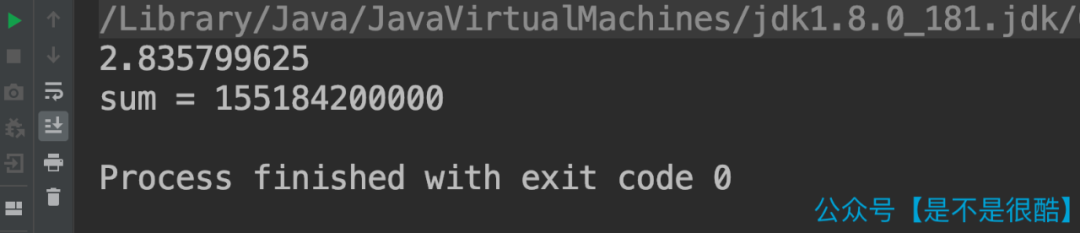
大家可以看到,由于測試數(shù)據(jù)是一樣的,所以最終的 sum?結(jié)果是一樣的。但是第二次,針對有序的數(shù)組做實驗,消耗的時間僅僅是 2.8 秒左右,比無序的情況快了有 3 倍之多!
大家可能會覺得,這是不是 JVM 在搞什么鬼?那么,同樣的代碼邏輯,我們嘗試用 C++ 實驗一遍!

這段代碼,我使用無序的數(shù)組測試,在我的計算機上,運行時間大概是 18.8 秒左右。(Debug 模式)
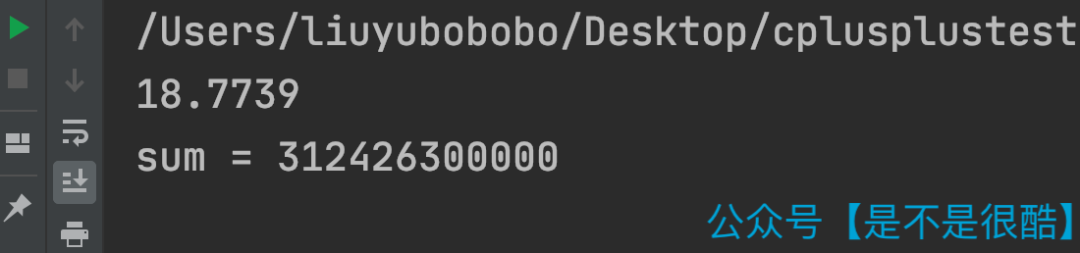
但是,當我將數(shù)組進行排序以后,運行時間則變成了 5.7 秒!(Debug 模式)
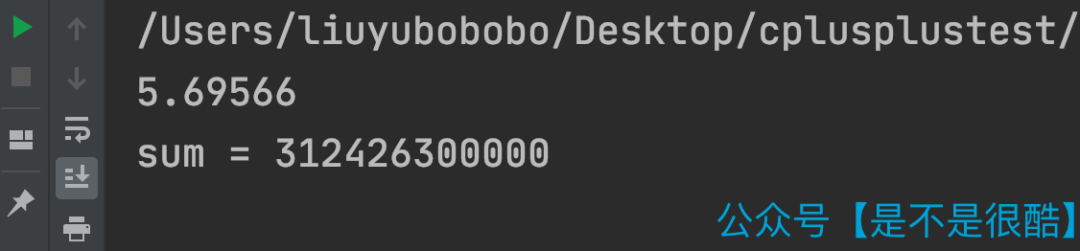
看來,這不是 JVM 的問題,而是有更加底層的優(yōu)化機制在起作用。
這個機制,就是 CPU 的分支預(yù)測(Branch prediction)。
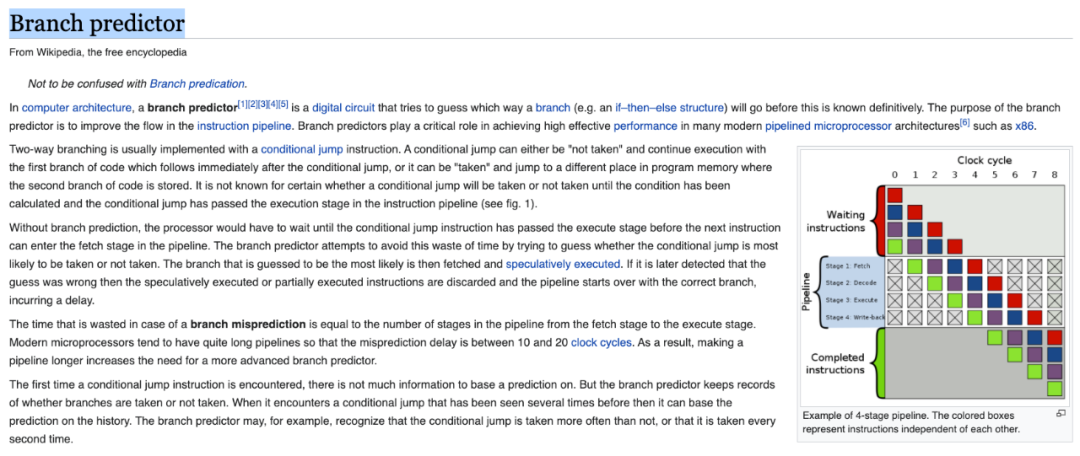
在具體講解什么是 CPU 的分支預(yù)測之前,我們先來看一下什么是 CPU 指令執(zhí)行的流水線(Pipeline)。
簡單來說,一條指令的執(zhí)行,在 CPU 內(nèi)部,需要經(jīng)過若干步驟。
比如,一個常見的模型,是 4 階段流水線。即一條指令在 CPU 內(nèi)部的執(zhí)行,需要有 4 步:
fetch(獲取指令) decode(解碼指令) execute(執(zhí)行指令) write-back(寫回數(shù)據(jù))
經(jīng)過這四個階段,才叫完全執(zhí)行完了一條指令。
我們可以類比這樣的一個例子。

我們?nèi)ズ芏嗦糜尉皡^(qū)吃飯,餐廳會使用半自助的形式由游客來選餐。游客進入選餐隊伍之后,需要完成以下的事情,才能真正的執(zhí)行完“買飯”這件事情,開始享用香噴噴的午餐:
選擇一個主菜 選擇一個配菜 選擇一個飲料 去結(jié)賬!
對于這個流程的執(zhí)行,我們當然可以等 A 同學(xué)選好他的午飯:主菜,配菜和飲料,并且結(jié)完賬,然后 B 同學(xué)再去選擇他的午飯。▼

相信同學(xué)們都明白,這樣做是低效的。
在 A 同學(xué)選擇完主菜,去選擇配菜的時候,B 同學(xué)就已經(jīng)可以上去選擇他的主菜了。▼

當 A 同學(xué)開始選擇飲料的時候,B 同學(xué)已經(jīng)可以選擇配菜了,而 C 同學(xué),此時就可以開始選擇主菜了。▼

這樣做,當 A 同學(xué)結(jié)完賬的時候,E 同學(xué)都已經(jīng)開始選主菜了。▼

很顯然,這樣做效率更高。
這就叫流水線。一個同學(xué)不需要等前一個同學(xué)完成所有選餐的步驟再去選餐,而只要完成一步,下一個同學(xué)就可以跟進。
CPU 的流水線完全同理。因為執(zhí)行每一條指令需要 4 步。所以,在執(zhí)行 A 指令的時候,一旦完成了 A 指令的 fetch 操作,進入 A 指令的 decode 階段,就可以對下一條 B 指令執(zhí)行 fetch 操作了。▼

當 A 指令 decode 完成,進入 execute 階段,就可以開始對 B 指令進行 decode 了,同時,B 指令的下一條 C 指令,就可以開始 fetch 了。▼

那么問題來了,現(xiàn)在,如果一條指令是 if,怎么辦?
為什么?if?指令會出問題?因為對于 if 指令,我們必須等它運行完,才能知道下一條指令是什么!下一條指令是根據(jù) if?表達式中的結(jié)果是真還是假來決定的!

而實際情況,可能不是簡單的一條指令的問題。因為 if?表達式的計算,可能涉及多個操作。
比如上面代碼中,就算是 if(data[c] >= 128)?這個簡單的邏輯,我們也需要先解析出 c?的值,再拿出 data,再從 data?中拿出 c?這個索引對應(yīng)的元素,再去比較這個元素是不是大于等于 128。
可以想象,后面的指令就停在這里了。需要等這一系列 if 判斷相關(guān)的指令都執(zhí)行完,計算出最終結(jié)果,才能決定下面把哪條指令放入流水線。
這顯然會對性能產(chǎn)生影響。于是,現(xiàn)代 CPU 對于這種情況,都設(shè)計了一個機制,叫做分支預(yù)測(Branch Prediction)。
簡單來說,分支預(yù)測就是針對這種 if?指令,不等它執(zhí)行完畢,先預(yù)測一下執(zhí)行的結(jié)果可能是 true?還是 false,然后將對應(yīng)條件的指令放進流水線。

如果等 if?語句執(zhí)行完畢,發(fā)現(xiàn)最初預(yù)測錯了,那么我們把這些錯誤的指令計算結(jié)果扔掉就好了,轉(zhuǎn)而重新把正確的指令放到流水線中執(zhí)行。
這種情況,雖然也會損失一些性能,但可以接受。因為反正如果不做預(yù)測,時間也會空耗,對應(yīng)就是 CPU 的時鐘周期空轉(zhuǎn)。
但一旦預(yù)測對了,那就是一個巨大的性能提升。因為后續(xù)指令已經(jīng)進入流水線,執(zhí)行起來了。我們直接繼續(xù)這個過程就好。
這就是 CPU 的分支預(yù)測,是不是很簡單?
具體 CPU 的分支預(yù)測是如何實現(xiàn)的?不同的體系架構(gòu),包括同一體系架構(gòu) CPU 的不同版本,會有不同的策略。
但是,整體上,一個重要的策略,是參考某條 if 指令執(zhí)行過程中判斷為 true 或者 false 的歷史記錄。
這應(yīng)用了在計算機領(lǐng)域經(jīng)常使用的一個原理:局部性原理。
通常在操作系統(tǒng)課程中,都會介紹這個重要的原理。很多算法或者數(shù)據(jù)結(jié)構(gòu)的設(shè)計,也是基于這個原理的。
比如,計算機體系結(jié)構(gòu)設(shè)計,都是分層的。從外存;到內(nèi)存;到一級緩存,二級緩存;到寄存器。存儲容量逐漸減小;但是,運算速度越來越快。
操作系統(tǒng)在運行的過程中,就需要做一個重要的調(diào)度:決定把什么數(shù)據(jù)放到更高層次的緩存中,以提升程序運行的效率。
局部性原理說的就是:
如果一個信息正在訪問,那么近期很有可能會再次訪問,這叫時間局部性;
如果一個信息正在訪問,那么近期訪問的其他信息,大概率在空間地址上,和這個信息的空間地址鄰近,這叫空間局部性。
這樣的局部性原理同樣被應(yīng)用在了 CPU 對 if?的條件分支預(yù)測上。一個 if?現(xiàn)在被判為 true,下次,會更高概率的判為 true。當然,實際的預(yù)測邏輯會更復(fù)雜,但是,局部性原理是一個重要的參考。
我稱之為:if 局部性原理。
(我瞎編的,聽說多使用這種讓人摸不到頭腦的術(shù)語,會顯得文章更加高大上。)

現(xiàn)在,大家應(yīng)該明白了。對于文章開始討論的代碼,如果數(shù)據(jù)經(jīng)過了排序,那么,所有小于 128 的數(shù)據(jù)就都在數(shù)組的前面;所有大于等于 128 的數(shù)據(jù),就都在數(shù)組的后面。
那么,在下面的執(zhí)行過程中,CPU 根據(jù)歷史記錄對 if 進行分支預(yù)測,就會高概率命中,提升性能。
而對于完全隨機的數(shù)組,數(shù)據(jù)是否大于等于 128 是完全隨機的,這就導(dǎo)致 CPU 的分支預(yù)測總是失效,從而,降低了性能。
好了,原理解釋清楚了。下面,我們看一下,在這個程序中,我們可不可以避免這種分支預(yù)測經(jīng)常失敗導(dǎo)致的性能問題?
答案是,可以!我們需要想辦法去掉 if 判斷。
怎么去除?在這個程序中,我們可以使用這樣的方式:
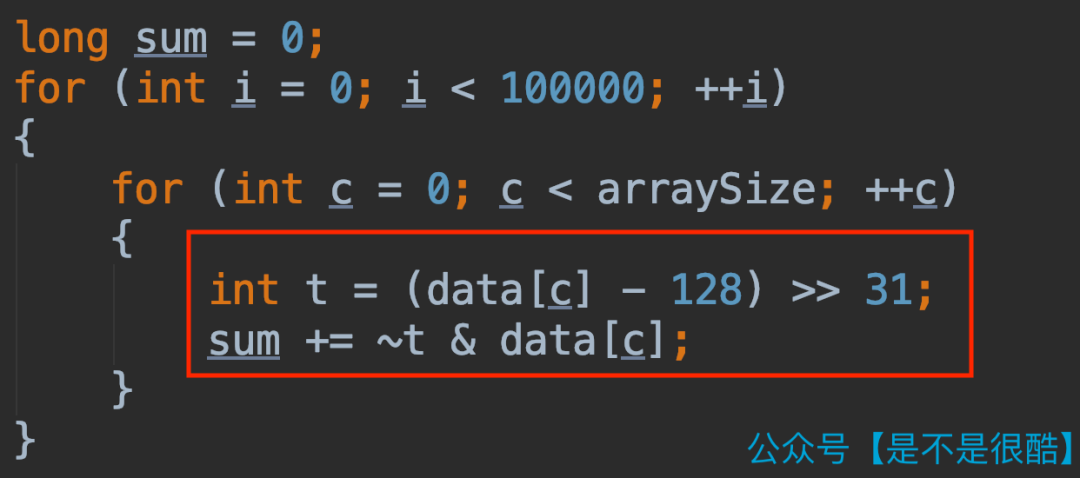
注意上面的代碼中,紅框的部分,代替了原來的 if 邏輯。
為什么這是等價的?我們可以簡單分析一下。
首先看變量 t 的值。他是 data[c] - 128 的結(jié)果右移 31 位。
大家可以想象:
如果 data[c] - 128 是非負數(shù),右移補零,符號位也是 0。右移 31 位的結(jié)果是 0x0000;
如果 data[c] - 128 是負數(shù),右移補一,符號位也是?1。右移 31 位的結(jié)果,是 0xffff。
在下面的 sum 計算中,先對 t 取反。
那么如果 data[c] - 128 是非負數(shù),即 data[c] >= 128,t 就是 0x0000,取反的結(jié)果是 0xffff。0xffff 每一位都是 1,和 data[c] 做與運算,結(jié)果還是 data[c] 自身。此時,相當于把 data[c] 加入了 sum 中。
如果 data[c] - 128 是負數(shù),即 data[c] < 128,t 就是 0xffff。此時對 t 取反,結(jié)果為 0。0 和 data[c] 做與運算,結(jié)果還是 0。此時,相當于 sum 什么都沒有加。
所以,這和判斷一下 data[c] 是否大于等于 128,如果大于等于,再做加法運算,是等價的。但是,我們?nèi)サ袅?if 判斷。
這個代碼的性能是怎樣的?在我的計算機上,不做排序的話,只需要 1.7 秒(對比之前的 8.4 秒)。

更重要的是,這個代碼的性能,不再受原始數(shù)組是否排序而影響。當排序以后,執(zhí)行時間,也是同一個數(shù)量級的。

使用 C++ 測試,結(jié)果是類似的。
怎么樣,是不是很酷?
關(guān)于分支預(yù)測,有興趣的同學(xué),可以參考維基百科的 Branch predictor 詞條,了解更多。
完
帥地搞了個小號,我會在這個公眾號分享讀者問過我的問題,并且給予最真實的回答,同時也會分享自己學(xué)習方法、掙錢經(jīng)歷、工作經(jīng)歷、個人經(jīng)歷、沙雕日常,我相信,我的經(jīng)歷與想法,一定可以給你帶來一些幫助!掃一掃進入帥地的私密沙雕小號
