程序猿聲

代碼黑科技的分享區(qū)

一、前言

小編有個小伙伴，隔三差五就過來跟我說：這個模型CPLEX怎么寫呢？我說我不是給你講過好多次？他說CPLEX太復(fù)雜了，俺沒學(xué)過學(xué)不會呢。其實對于很多剛?cè)胄械男』锇閬碚f，CPLEX算不上友好，就連學(xué)習(xí)資料都不知道去哪里看，不像Excel或者Word，百度一下出來好多資料。

其實吧，這玩意兒并沒有大家想的那么難，尤其是簡單使用CPLEX求解一個模型的話，用來用去都是那幾個函數(shù)而已。下面小編來給大家好好理一下，看完相信你也能用CPLEX跑一下論文上的模型啦。

當(dāng)然啦，為了方便小編還是選擇大家熟悉的Java平臺，用Python也是可以的，處理數(shù)據(jù)可能還更方便。但是我們一般都是用Java寫的算法，因此就統(tǒng)一平臺啦。我們今天以一個最經(jīng)典的VRPTW arc-flow model為例，手把手給大家演示下，CPLEX其實并不是那么的難用。

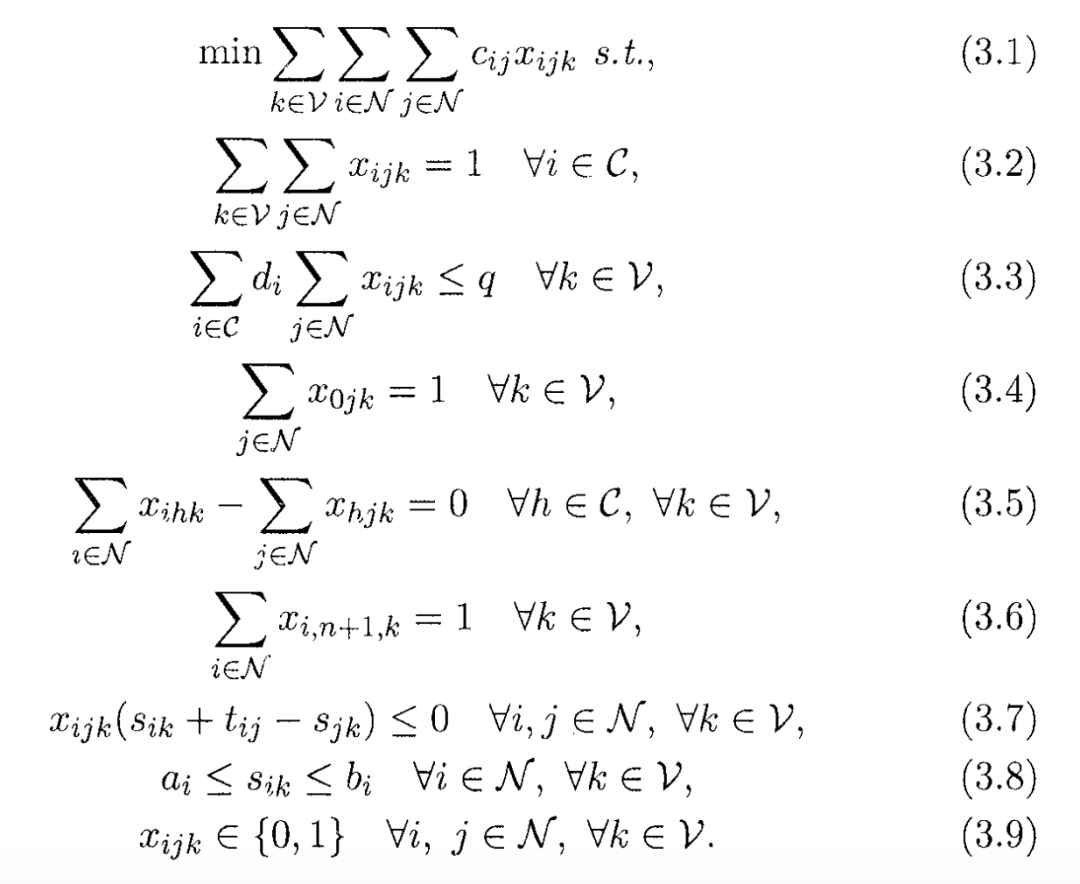
二、模型集合定義

運行一個模型之前，首先要定義模型中用到的一些參數(shù)和集合，如果這些都沒有，是無從談起的。因此沒有的話第一步是要先生成這些數(shù)據(jù)哦。

2.1 讀取數(shù)據(jù)

首先，你需要在程序中定義相關(guān)的變量（通常的做法是寫一個instance的類，把算例的數(shù)據(jù)讀進(jìn)來，放到成員變量上。）比如：

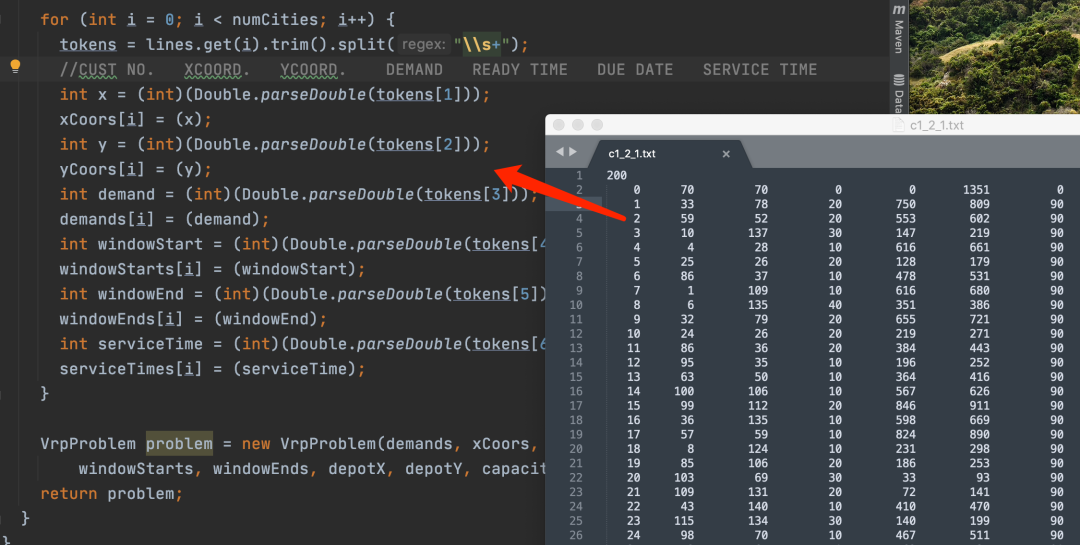
至于你怎么定義怎么寫都無所謂啦，反正你知道這些數(shù)據(jù)對應(yīng)模型的哪些參數(shù)就可以啦。

2.2 定義集合

其實小編發(fā)現(xiàn)，大家之所以覺得寫模型難，還有一個原因就是自己建模的時候純粹瞎搞。很多集合啊，參數(shù)啊，范圍啊都沒有想清楚，到寫代碼的時候就各種凌亂了。。。

好了回到我們的正題，剛剛讀入了算例。接下來我們需要定義模型中需要用到的集合，這些集合是哪些集合呢？就是我指出來的這些：

然后你需要在程序中把這些集合給定義好了，然后把相應(yīng)的數(shù)據(jù)填充進(jìn)去，比如為所有節(jié)點的集合，為所有車輛集合，那么就for一下填充就好啦：

for(i?=?0;?i?2;?++i){
???this.N.add(i);
}

for(i?=?0;?i?????this.K.add(i);
}

當(dāng)然了，在程序中不用定義這些集合也能實現(xiàn)我們的模型，這樣做只是為了讓程序更清晰，不至于到后面雜亂無章，debug起來也無從下手。

三、CPLEX建模

做完數(shù)據(jù)的定義，基本上就成功50%了。就像追女孩紙一樣，當(dāng)你喜歡她的時候就成功了50%，當(dāng)她再喜歡你的時候，就100%成功了。現(xiàn)在我們就來完成剩下的50%。

在CPLEX中，你只需要知道以下三點，就能輕松駕馭一個數(shù)學(xué)模型啦：

決策變量定義
添加優(yōu)化目標(biāo)
添加約束

想想也是哦，一個數(shù)學(xué)模型無非就是由決策變量、優(yōu)化目標(biāo)和約束組成嘛。下面我們來一個一個講解。

不過，在此之前，我們先new一個CPLEX的對象出來，并設(shè)置一些參數(shù)：

this.cplex?=?new?IloCplex();
this.cplex.setParam(IloCplex.Param.Simplex.Tolerances.Optimality,?1e-9);
this.cplex.setParam(IloCplex.Param.MIP.Tolerances.MIPGap,?1e-9);
this.cplex.setParam(IloCplex.DoubleParam.TimeLimit,?3600);
this.cplex.setOut(null);

第一第二句是求解精度相關(guān)的設(shè)置。倒數(shù)第二句表示設(shè)置求解時間為3600s，比較常用。最后一句是告訴CPLEX不要輸出那些亂七八糟的東西，太煩啦！

3.1 決策變量的定義

首先是模型中有哪些變量，通通得定義出來。在CPLEX的Java API中，一個決策變量是一個對象來的，首先我們需要定義決策變量的數(shù)組，并分配數(shù)組的空間，比如的：

this.x?=?new?IloNumVar[n+1][n+1][v];?

IloNumVar這個表示它是一個num也就是數(shù)值類型的變量，就是可以為浮點數(shù)也可以為整數(shù)。這里我們只分配了數(shù)組空間，接下來還需要為里面的每個引用分配一個對象（分配了房子，再給它發(fā)媳婦！）：

//分配內(nèi)存
//x?0-1變量?[n+1][n+1][v];
for(int?i?=?0;?i?1;?++i){
????for(int?j?=?0;?j?1;?++j){
????????for(int?k?=?0;?k?????????????x[i][j][k]?=?cplex.numVar(0,?1,?IloNumVarType.Int,?"x["+i+"]["+j+"]["+k+"]");
????????}
????}
}

其中cplex.numVar()這個函數(shù)呢就為我們new了一個數(shù)值變量的對象出來，我這里貼上官方的解釋好啦：

如果你有不同類型的變量，指定下第三個參數(shù)IloNumVarType就好啦：

模型中另一個決策變量類似，我就不寫啦。

3.2 CPLEX的表達(dá)式

首先來看一個概念：表達(dá)式是什么呢？吶，類似于我圈出來的這些：

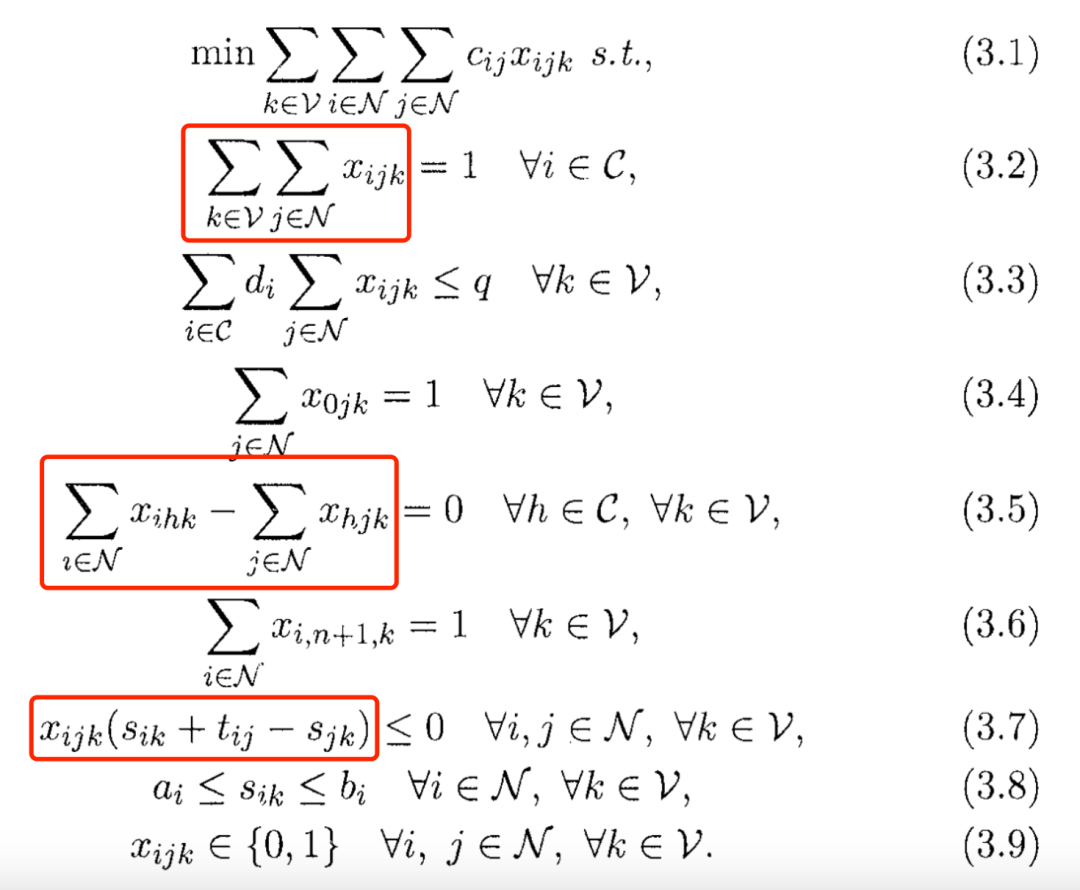
開始的時候，一般需要new一條IloNumExpr類型的空表達(dá)式出來，然后慢慢去填充它：

IloNumExpr?expr?=?this.cplex.numExpr();

創(chuàng)建空表達(dá)式可以通過numExpr()函數(shù)哦：

在CPLEX的JavaAPI中呢，涉及到CPLEX對象的一些表達(dá)式，是不能直接通過Java自帶的+-*/進(jìn)行運算的。需要通過CPLEX提供sum()、diff()、prod()函數(shù)進(jìn)行加、減、乘的操作。

那為什么沒有除呢？因為除是可以通過轉(zhuǎn)換變成乘的！比如可以轉(zhuǎn)換成，沒毛病吧~

其中，sum()、diff()、prod()這些函數(shù)在CPLEX的庫中重載了很多版本，也就是說你sum(IloNumExpr, double)、sum(IloNumExpr, IloNumExpr)、sum(double, IloNumExpr)都是可以識別的，那么我就貼一個出來給大家看看就好啦：

sum()、diff()也是類似的，不過需要注意的是diff()時要注意區(qū)分是誰減去誰哦。現(xiàn)在表達(dá)式有了，我們來看看怎樣通過sum()、diff()、prod()這些函數(shù)，實現(xiàn)模型中的式子。以目標(biāo)那個式子為例：

有三個求和符號，那么肯定得來三個循環(huán)啦：

IloNumExpr?objExpr?=?this.cplex.numExpr();
for(k?:?this.K){
????for(i?:?this.N){
????????for(j?:?this.N){
????????????IloNumExpr?subExpr?=?this.cplex.prod(c[i][j],?this.x[i][j][k]);
????????????obj?=?this.cplex.sum(obj,?subExpr);
????????}
????}
}

可能這一句obj = this.cplex.sum(obj, subExpr);大家有點暈，其實很簡單，就是obj和subExpr相加，得到一個新的表達(dá)式，再賦值給obj。那么這樣就能實現(xiàn)累加的效果了，大部分的求和表達(dá)式都可以寫成這種形式哦。

3.3 添加目標(biāo)和約束

好了，知道了表達(dá)式，添加目標(biāo)和約束就變得非常簡單啦。首先是目標(biāo)的添加，CPLEX中提供了兩個函數(shù)：addMinimize()和addMaximize()分別用以添加最小化目標(biāo)和最大化目標(biāo)。根據(jù)自己的需要調(diào)用就好，當(dāng)然這兩個函數(shù)也是有很多重載的版本，我就放一個最常用的給大家看看吧：

參數(shù)就是一個IloNumExpr類型的表達(dá)式，比如可以直接把上面的objExpr給add進(jìn)來，是不是很簡單呢！

對于添加約束，CPLEX也提供了三個函數(shù)，我這里寫成一個表格方便大家查看：

method	作用
addGe(a, b)	添加約束
addLe(a, b)	添加約束
addEq(a, b)	添加約束

根據(jù)a，b類型的不同，這幾個函數(shù)同樣重載了很多版本，你寫addGe(IloNumExpr, double)、addGe(IloNumExpr, IloNumExpr)、addGe(double, IloNumExpr)都是可以的。我放一個官方的介紹吧：

現(xiàn)在，我們來看看一個example，演示下如何添加約束（3.5）：

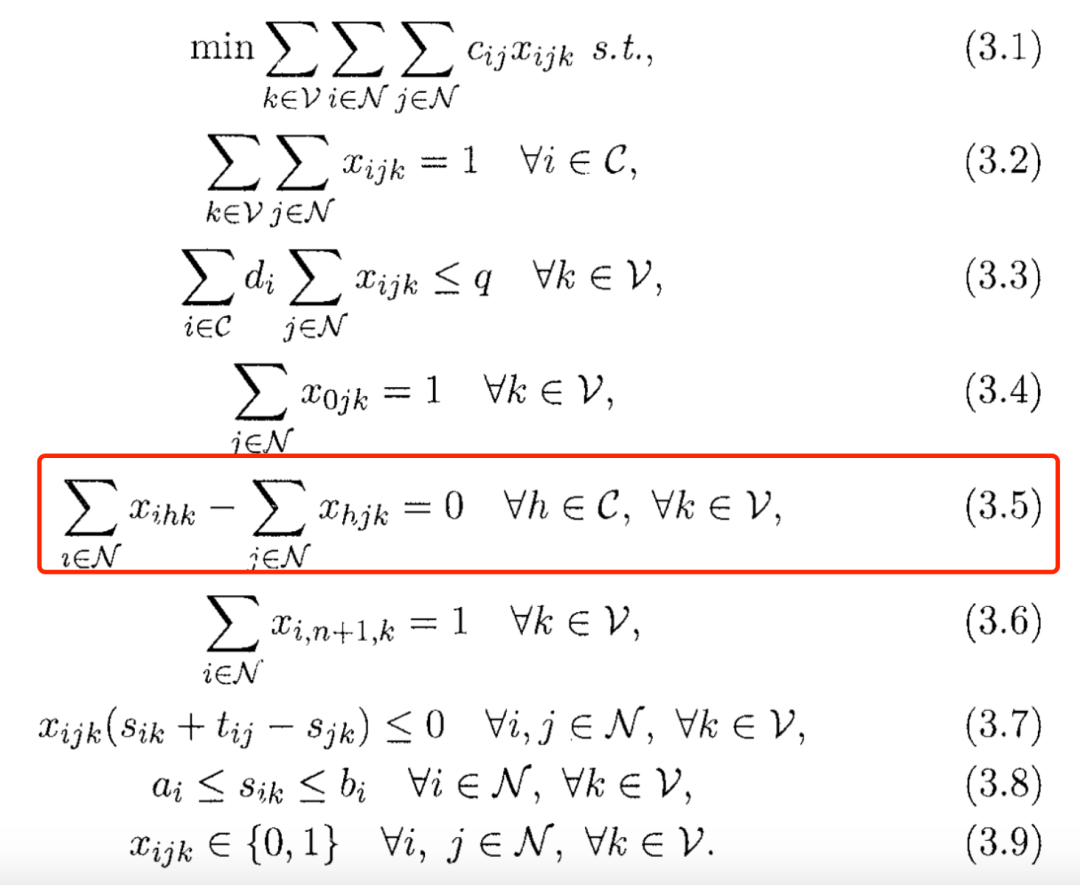
首先，從哪著手呢？從右邊開始：對于任意的，任意的，都要滿足左邊那個等式。兩個循環(huán)是沒跑了，然后在循環(huán)的最內(nèi)層，把相關(guān)表達(dá)式給addEq就好了：

for(h?:?this.C){
????for(k?:?this.V){
????????//這里要開始寫表達(dá)式啦
????????IloNumExpr?subExpr1?=?this.cplex.numExpr();
????????IloNumExpr?subExpr2?=?this.cplex.numExpr();
????????for(i?:?this.N){
????????????subExpr1?=?this.cplex.sum(subExpr1,?this.x[i][h][k]);
????????????subExpr2?=?this.cplex.sum(subExpr1,?this.x[h][j][k]);
????????}
????????cplex.addEq(subExpr1,?subExpr2);
????}
}