運(yùn)籌學(xué)自二戰(zhàn)誕生以來(lái)，現(xiàn)已被廣泛應(yīng)用于工業(yè)生產(chǎn)領(lǐng)域了，比如交通運(yùn)輸、供應(yīng)鏈、能源、經(jīng)濟(jì)以及生產(chǎn)調(diào)度等。離散優(yōu)化問題（discrete optimization problems）是運(yùn)籌學(xué)中非常重要的一部分，他們通常可以建模成整數(shù)優(yōu)化模型進(jìn)行求解，即通過決定一系列受約束的整數(shù)或者0-1變量，得出模型最優(yōu)解。

有一些組合優(yōu)化問題不是那么的“難”，比如最短路問題，可以在多項(xiàng)式的時(shí)間內(nèi)進(jìn)行求解。然而，對(duì)于一些NP-hard問題，就無(wú)法在多項(xiàng)式時(shí)間內(nèi)求解了。簡(jiǎn)而言之，這類問題非常復(fù)雜，實(shí)際上現(xiàn)在的組合優(yōu)化算法最多只能求解幾百萬(wàn)個(gè)變量和約束的問題而已。

機(jī)器學(xué)習(xí)是一門多領(lǐng)域交叉學(xué)科，涉及概率論、統(tǒng)計(jì)學(xué)、逼近論、凸分析、算法復(fù)雜度理論等多門學(xué)科。現(xiàn)在，有很多研究想將學(xué)習(xí)的方法應(yīng)用與組合優(yōu)化領(lǐng)域，提高傳統(tǒng)優(yōu)化算法的效率。

By the way，大家請(qǐng)?jiān)徫遥行﹩卧~我真不知道咋翻譯，就直接用英文了，所以你們閱讀的時(shí)候看見中英混用，絕不是我在裝13，而是有些情景用英文大家理解起來(lái)會(huì)更方便。

1 動(dòng)機(jī)

在組合優(yōu)化算法中使用機(jī)器學(xué)習(xí)的方法，主要有兩方面：

（1）優(yōu)化算法中某些模塊計(jì)算非常消耗時(shí)間和資源，可以利用機(jī)器學(xué)習(xí)得出一個(gè)近似的值，從而加快算法的速度。

（2）現(xiàn)存的一些優(yōu)化方法效果并不是那么顯著，希望通過學(xué)習(xí)的方法學(xué)習(xí)搜索最優(yōu)策略過程中的一些經(jīng)驗(yàn)，提高當(dāng)前算法的效果。（算是一種新思路？）

2 介紹

這一節(jié)簡(jiǎn)要介紹下關(guān)于組合優(yōu)化和機(jī)器學(xué)習(xí)的一些概念，當(dāng)然，只是粗略的看一下，詳細(xì)內(nèi)容大家還是去參照以往公眾號(hào)的文章（指的組合優(yōu)化方面）。因?yàn)橹白龅囊恢笔沁\(yùn)籌優(yōu)化領(lǐng)域，對(duì)機(jī)器學(xué)習(xí)一知半解，所以關(guān)于這部分的闡述則是從網(wǎng)上篩選過來(lái)的，出處我均已貼到參考那里了。

2.1 組合優(yōu)化

組合優(yōu)化相信大家都很熟悉了，因?yàn)楣娞?hào)一直在做的就是這方面的內(nèi)容。一個(gè)組合優(yōu)化問題呢通常都能被建模成一個(gè)帶約束的最小化問題進(jìn)行求解，即將問題以數(shù)學(xué)表達(dá)式的形式給出，通過約束變量的范圍，讓變量在可行域內(nèi)作出決策，使得目標(biāo)值最小的過程。

如果決策變量是線性的，那么該問題可以稱為線性規(guī)劃（Linear programming）；如果決策變量是整數(shù)或者0-1，那么可以稱為整數(shù)規(guī)劃（Integer programming）；而如果決策變量是整數(shù)和線性混合的，那么可以稱為混合整數(shù)規(guī)劃（Mixed-integer programming）。可以利用branch and bound算法解決Mixed-integer programming問題，目前應(yīng)用的比較多，也有很多成熟的求解器了，比如cplex、lpsolve、國(guó)產(chǎn)的solver等等。但是就目前而言，求解器在求解效率上仍存在著問題，難以投入到實(shí)際的工業(yè)應(yīng)用中，現(xiàn)在業(yè)界用啟發(fā)式比較多。

2.2 監(jiān)督學(xué)習(xí)(supervised learning)

監(jiān)督學(xué)習(xí)(supervised learning)的任務(wù)是學(xué)習(xí)一個(gè)模型，使模型能夠?qū)θ我饨o定的輸入，對(duì)其相應(yīng)的輸出做一個(gè)好的預(yù)測(cè)。監(jiān)督學(xué)習(xí)其實(shí)就是根據(jù)已有的數(shù)據(jù)集，知道輸入與輸出的結(jié)果之間的關(guān)系，然后根據(jù)這種關(guān)系訓(xùn)練得到一個(gè)最優(yōu)的模型。

2.3 強(qiáng)化學(xué)習(xí)(Reinforcement learning)

強(qiáng)化學(xué)習(xí)（Reinforcement Learning, RL），又稱再勵(lì)學(xué)習(xí)、評(píng)價(jià)學(xué)習(xí)或增強(qiáng)學(xué)習(xí)，是機(jī)器學(xué)習(xí)的范式和方法論之一，用于描述和解決智能體（agent）在與環(huán)境的交互過程中通過學(xué)習(xí)策略以達(dá)成回報(bào)最大化或?qū)崿F(xiàn)特定目標(biāo)的問題。[百度百科]

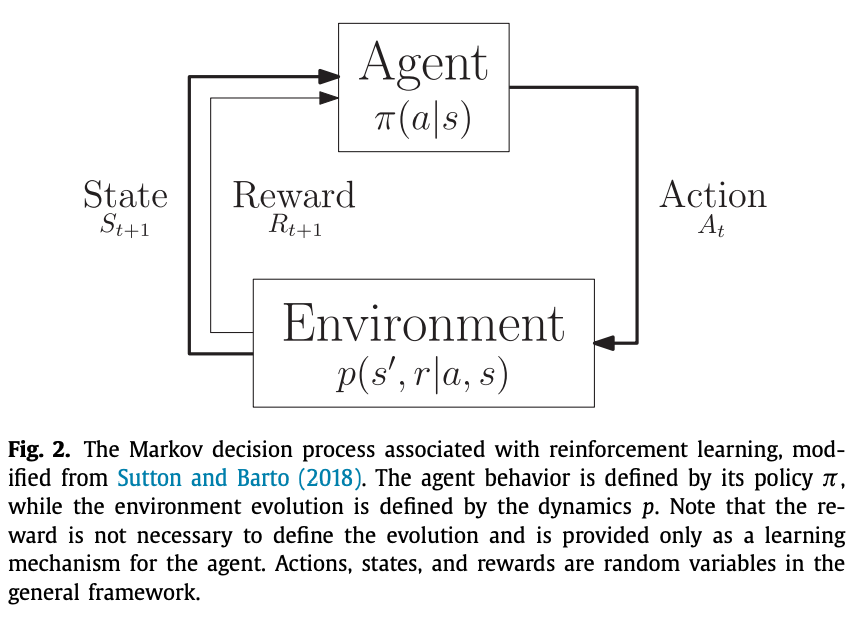
馬爾可夫決策過程（Markov Decision Processes,MDPs） MDPs 簡(jiǎn)單說就是一個(gè)智能體（Agent）采取行動(dòng)（Action）從而改變自己的狀態(tài)（State）獲得獎(jiǎng)勵(lì)（Reward）與環(huán)境（Environment）發(fā)生交互的循環(huán)過程。

MDP 的策略完全取決于當(dāng)前狀態(tài)（Only present matters），這也是它馬爾可夫性質(zhì)的體現(xiàn)。

先行動(dòng)起來(lái)，如果方向正確那么就繼續(xù)前行，如果錯(cuò)了，子曰：過則勿憚改。吸取經(jīng)驗(yàn)，好好改正，失敗乃成功之母，從頭再來(lái)就是。總之要行動(dòng)，胡適先生說：怕什么真理無(wú)窮，進(jìn)一寸有一寸的歡喜。

即想要理解信息，獲得輸入到輸出的映射，就需要從自身的以往經(jīng)驗(yàn)中去不斷學(xué)習(xí)來(lái)獲取知識(shí)，從而不需要大量已標(biāo)記的確定標(biāo)簽，只需要一個(gè)評(píng)價(jià)行為好壞的獎(jiǎng)懲機(jī)制進(jìn)行反饋，強(qiáng)化學(xué)習(xí)通過這樣的反饋?zhàn)约哼M(jìn)行“學(xué)習(xí)”。（當(dāng)前行為“好”以后就多往這個(gè)方向發(fā)展，如果“壞”就盡量避免這樣的行為，即不是直接得到了標(biāo)簽，而是自己在實(shí)際中總結(jié)得到的）

3 近來(lái)的研究

第1節(jié)的時(shí)候，我們提到了在組合優(yōu)化中使用機(jī)器學(xué)習(xí)的兩種動(dòng)機(jī)，那么現(xiàn)在很多研究也是圍繞著這兩方面進(jìn)行展開的。

首先說說動(dòng)機(jī)（1），期望使用機(jī)器學(xué)習(xí)來(lái)快速得出一個(gè)近似值，從而減少優(yōu)化算法中某些模塊的計(jì)算負(fù)擔(dān)，加快算法的速度。比如說在branch and price求解VRP類問題中，其子問題SPPRC的求解就是一個(gè)非常耗時(shí)的模塊，如果利用機(jī)器學(xué)習(xí)，在column generation的每次迭代中能快速生成一些reduced cost為負(fù)的路徑，那整個(gè)算法的速度就非常快了。不過這個(gè)難度應(yīng)該會(huì)非常大，希望若干年后能實(shí)現(xiàn)吧~

而動(dòng)機(jī)（2）則是嘗試一種新的思路來(lái)解決組合優(yōu)化問題吧，讓機(jī)器學(xué)習(xí)算法自己去學(xué)習(xí)策略，從而應(yīng)用到算法中。比如branch and bound中關(guān)于branch node的選取，選擇的策略能夠極大地影響算法運(yùn)行的時(shí)間，目前常見的有深度優(yōu)先、廣度優(yōu)先等。但這些方法效果遠(yuǎn)沒有那么出眾，所以寄希望于新興的機(jī)器學(xué)習(xí)方法，期望能得到一些新的，outstanding的策略。

動(dòng)機(jī)（1）和動(dòng)機(jī)（2）下所使用的機(jī)器學(xué)習(xí)方法也是不同的，在開始介紹之前呢，大家先去回顧下第2節(jié)中介紹強(qiáng)化學(xué)習(xí)時(shí)提到的Markov鏈。假設(shè)environment是算法內(nèi)部當(dāng)前的狀態(tài)，我們比較關(guān)心的是組合優(yōu)化算法中某個(gè)使用了機(jī)器學(xué)習(xí)來(lái)做決策的函數(shù)，該函數(shù)在當(dāng)前給定的所有信息中，返回一個(gè)將要被算法執(zhí)行的action，我們暫且叫這樣的一個(gè)函數(shù)為policy吧。

那么這樣的policy是怎樣給出相應(yīng)的action呢？所謂機(jī)器學(xué)習(xí)，當(dāng)然是通過學(xué)習(xí)！而學(xué)習(xí)也有很多方式，比如有些人不喜歡聽老師口口相傳，只喜歡不聽地做題，上課也在不停的刷題刷題（小編我）。有些人就上課認(rèn)認(rèn)真真聽課，課后重點(diǎn)復(fù)習(xí)老師講的內(nèi)容。所有的方式，目的都是為了獲得知識(shí)，考試考高分。同樣的，在兩種動(dòng)機(jī)下，policy學(xué)習(xí)的方式也是不一樣的，我們且稱之為learning setting吧。

動(dòng)機(jī)（1）下使用的是demonstration setting，他是一種模仿學(xué)習(xí)，蹣跚學(xué)步大家聽過吧~這種策略呢就是不斷模仿expert做的決策進(jìn)行學(xué)習(xí)，也沒有什么reward啥的，反正你怎么做我也怎么做。他是通過一系列的“樣例”進(jìn)行學(xué)習(xí)，比如你把TSP問題的輸入和最優(yōu)解打包丟給他，讓他進(jìn)行學(xué)習(xí)，當(dāng)他學(xué)有所成時(shí)，你隨便輸入一個(gè)TSP的數(shù)據(jù)，他馬上（注意是非常快速的）就能給出一個(gè)結(jié)果。這個(gè)結(jié)果有可能是最優(yōu)的，也有可能是近似最優(yōu)的。當(dāng)然，下面會(huì)舉更詳細(xì)的例子進(jìn)行介紹。如下圖所示，在demonstration setting下，學(xué)習(xí)的目標(biāo)是盡可能使得policy的action和expert相近。

動(dòng)機(jī)（2）意在發(fā)現(xiàn)新的策略，policy是使用reinforcement learning通過experience進(jìn)行學(xué)習(xí)的。他是通過一種action-reward的方式，訓(xùn)練policy，使得它不斷向最優(yōu)的方向改進(jìn)。當(dāng)然了，這里為了獲得最大的reward，除了使用reinforcement learning algorithms的方法，也可以使用一些經(jīng)典的optimization methods，比如genetic algorithms, direct/local search。

簡(jiǎn)單總結(jié)一下，動(dòng)機(jī)（1）中的模仿學(xué)習(xí)，其實(shí)是采用expert提供的一些target進(jìn)行學(xué)習(xí)（沒有reward）。而動(dòng)機(jī)（2）中的經(jīng)驗(yàn)學(xué)習(xí)，是采用reinforcement learning從reward中不斷修正自己（沒有expert）。在動(dòng)機(jī)（1）中，agent is taught what to do。而在動(dòng)機(jī)（2）中，agent is encouraged to quickly accumulate rewards。

3.1 demonstration setting

這一節(jié)介紹下目前使用demonstration setting的一些研究現(xiàn)狀。（挑幾個(gè)有代表性的講講，詳情大家去看paper吧~）

我們知道，在求解線性規(guī)劃時(shí)，通過添加cutting plane可以tighten當(dāng)前的relaxation，從而獲得一個(gè)更好的lower bound，暫且將加入cutting plane后lower bound相比原來(lái)提升的部分稱之為improvement吧。Baltean-Lugojan et al. (2018) 使用了一個(gè)neural network去對(duì)求解過程中的improvement進(jìn)行了一個(gè)近似。具體做法大家直接去看文獻(xiàn)吧，畢竟有點(diǎn)專業(yè)。

第二個(gè)例子，就是我們之前說過的，使用branch and bound求解mixed integer programming的時(shí)候，如果選擇分支的節(jié)點(diǎn)，非常重要。一個(gè)有效的策略，能夠大大減少分支樹的size，從而節(jié)省大量的計(jì)算時(shí)間。目前表現(xiàn)比較好的一個(gè)heuristic策略是strong branching (Applegate, Bixby, Chva?tal, & Cook, 2007)，該策略計(jì)算眾多候選節(jié)點(diǎn)的linear relaxation，以獲得一個(gè)potential lower bound improvement，最終選擇improvement最大那個(gè)節(jié)點(diǎn)進(jìn)行分支。盡管如此，分支的節(jié)點(diǎn)數(shù)目還是太大了。因此，Marcos Alvarez, Louveaux, and Wehenkel (2014, 2017)使用了一個(gè)經(jīng)典的監(jiān)督學(xué)習(xí)模型去近似strong branching的決策。He, Daume III, and Eisner (2014)學(xué)習(xí)了這樣的一個(gè)策略--選擇包含有最優(yōu)解的分支節(jié)點(diǎn)進(jìn)行分支，該算法是通過整個(gè)分支過程不斷收集expert的behaviors來(lái)進(jìn)行學(xué)習(xí)的。

3.2 experience

開局先談?wù)劥蠹曳浅Ｊ煜さ腡SP問題，在TSP問題中，獲得一個(gè)可行解是非常容易的一件事，我們只需要依次從未插入的節(jié)點(diǎn)中選擇一個(gè)節(jié)點(diǎn)并將其插入到解中，當(dāng)所有節(jié)點(diǎn)都插入到解中時(shí)，就可以得到一個(gè)可行解。在貪心算法中，每次選擇一個(gè)距離上次插入節(jié)點(diǎn)最近的節(jié)點(diǎn)，當(dāng)然我們最直接的做法也是這樣的。但是這樣的效果，并沒有那么的好，特別是在大規(guī)模的問題中。具體可以參考下面這篇推文：

Khalil, Dai, Zhang, Dilkina, and Song (2017a)構(gòu)建了一個(gè)貪心的啟發(fā)式框架，其中節(jié)點(diǎn)的選擇用的是graph neural network，一種能通過message passing從而處理任意有限大小graphs的neural network。對(duì)于每個(gè)節(jié)點(diǎn)的選擇，首先將問題的網(wǎng)絡(luò)圖，以及一些參數(shù)（指明哪些點(diǎn)以及被Visited了）輸入到neural network中，然后獲得每個(gè)節(jié)點(diǎn)的action value，使用reinforcement learning對(duì)這些action value進(jìn)行學(xué)習(xí)，reward的使用的是當(dāng)前解的一個(gè)路徑長(zhǎng)度。

結(jié)尾

今天先介紹這么多了。以上內(nèi)容都是小編閱讀論文

Machine learning for combinatorial optimization: A methodological tour d’horizon

所得的，基本上翻譯+自己理解。但是這個(gè)paper還沒講完哦，后面還有些許的內(nèi)容，容我下篇推文再介紹啦。急不可耐的小伙伴可以直接去看原paper哦。

參考

監(jiān)督學(xué)習(xí)(supervised learning)的介紹 https://zhuanlan.zhihu.com/p/99022922

強(qiáng)化學(xué)習(xí)（Reinforcement Learning）知識(shí)整理 https://zhuanlan.zhihu.com/p/25319023

強(qiáng)化學(xué)習(xí)（Q-Learning，Sarsa） https://blog.csdn.net/qq_39388410/article/details/88795124

Baltean-Lugojan, R., Misener, R., Bonami, P., & Tramontani, A. (2018). Strong Sparse Cut Selection via Trained Neural Nets for Quadratic Semidefinite Outer-Approx- imations. Technical Report. Imperial College, London.

Applegate, D., Bixby, R., Chva?tal, V., & Cook, W. (2007). The Traveling Salesman Prob- lem: A Computational Study. Princeton University Press.

Marcos Alvarez, A., Louveaux, Q., & Wehenkel, L. (2014). A supervised machine learning approach to variable branching in branch-and-bound. Technical Report. Universite? de Lie?ge.

Marcos Alvarez, A., Louveaux, Q., & Wehenkel, L. (2017). A machine learning-based approximation of strong branching. INFORMS journal on computing, 29(1), 185–195.

He, H., Daume III, H., & Eisner, J. M. (2014). Learning to search in branch and bound algorithms. In Z. Ghahramani, M. Welling, C. Cortes, N. D. Lawrence, & K. Q. Weinberger (Eds.), Advances in neural information processing systems 27(pp. 3293–3301). Curran Associates, Inc.

Khalil, E., Dai, H., Zhang, Y., Dilkina, B., & Song, L. (2017a). Learning combinatorial optimization algorithms over graphs. In I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan, & R. Garnett (Eds.), Advances in Neural Information Processing Systems 30 (pp. 6348–6358). Curran Associates, Inc..