八大必知必會的排序算法(Python)
一、插入排序
介紹 ? ? ? 插入排序的基本操作就是將一個數(shù)據(jù)插入到已經(jīng)排好序的有序數(shù)據(jù)中,從而得到一個新的、個數(shù)加一的有序數(shù)據(jù)。 ? ? ? 算法適用于少量數(shù)據(jù)的排序,時間復雜度為O(n^2)。 ? ? ? 插入排算法是穩(wěn)定的排序方法。
步驟 ????????①從第一個元素開始,該元素可以認為已經(jīng)被排序 ????????②取出下一個元素,在已經(jīng)排序的元素序列中從后向前掃描 ????????③如果該元素(已排序)大于新元素,將該元素移到下一位置 ????????④重復步驟3,直到找到已排序的元素小于或者等于新元素的位置 ????????⑤將新元素插入到該位置中 ????????⑥重復步驟2
排序演示
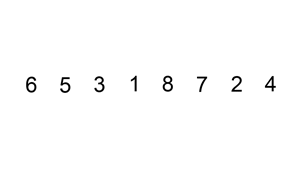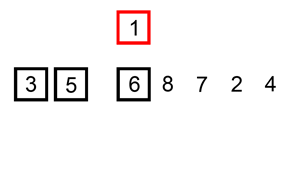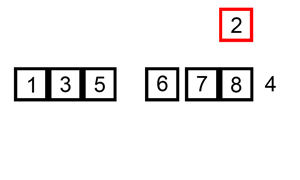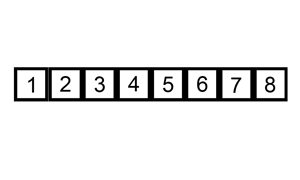
算法實現(xiàn)
# 插入排序
def insert_sort(lists):
count = len(lists)
for i in range(1, count):
key = lists[i]
j = i - 1
while j >= 0:
if lists[j] > key:
lists[j + 1] = lists[j]
lists[j] = key
j -= 1
return lists
二、冒泡排序
介紹 ? ? ? 冒泡排序(Bubble Sort)是一種簡單的排序算法,時間復雜度為O(n^2)。
? ? ? 它重復地走訪過要排序的數(shù)列,一次比較兩個元素,如果他們的順序錯誤就把他們交換過來。走訪數(shù)列的工作是重復地進行直到?jīng)]有再需要交換,也就是說該數(shù)列已經(jīng)排序完成。
? ? ? 這個算法的名字由來是因為越小的元素會經(jīng)由交換慢慢“浮”到數(shù)列的頂端。
原理 ? ??? ?循環(huán)遍歷列表,每次循環(huán)找出循環(huán)最大的元素排在后面; ? ? ? ?需要使用嵌套循環(huán)實現(xiàn):外層循環(huán)控制總循環(huán)次數(shù),內(nèi)層循環(huán)負責每輪的循環(huán)比較。
步驟 ? ? ? ?①比較相鄰的元素。如果第一個比第二個大,就交換他們兩個。 ? ? ? ?②對每一對相鄰元素作同樣的工作,從開始第一對到結(jié)尾的最后一對。在這一點,最后的元素應該會是最大的數(shù)。 ? ? ? ?③針對所有的元素重復以上的步驟,除了最后一個。 ? ? ? ?④持續(xù)每次對越來越少的元素重復上面的步驟,直到?jīng)]有任何一對數(shù)字需要比較。
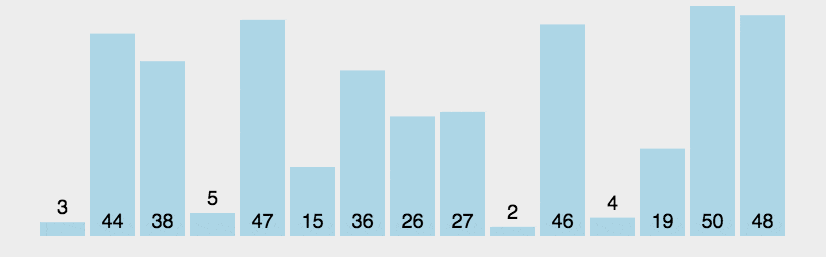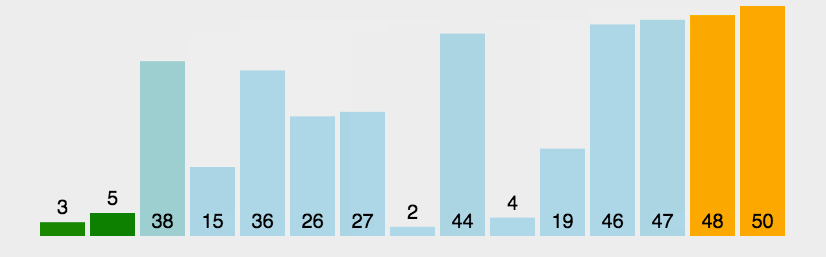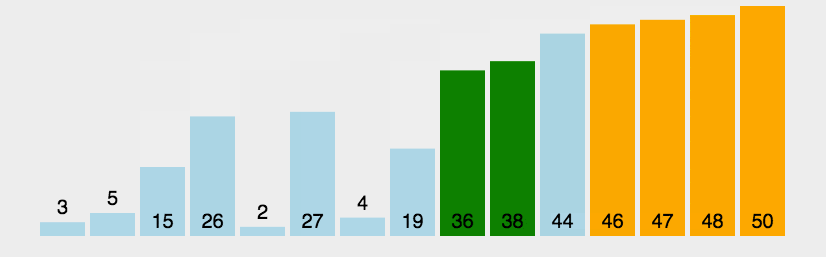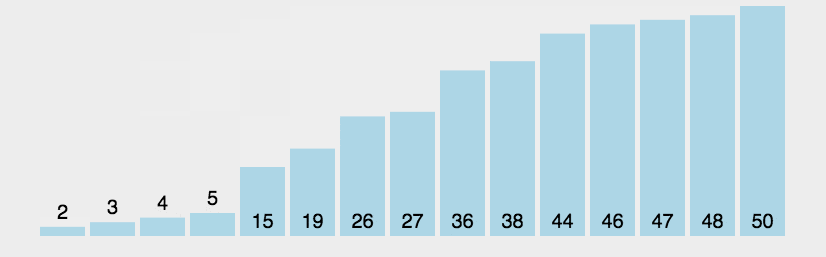
算法實現(xiàn):
# 冒泡排序
'''
排序的總輪數(shù)=列表元素個數(shù) - 1
每輪元素互相比較的次數(shù) = 列表元素個數(shù) - 已經(jīng)排好序的元素個數(shù) - 1
'''
def bubble_sort(data_list):
num = len(data_list) #列表元素個數(shù)
for i in range(0,num -1):#排序的總輪數(shù)
print("第{}輪:".format(i))
for j in range(0,num-i-1):
if data_list[j] > data_list[j+1]:#前后兩個元素比較
data_list[j],data_list[j+1] = data_list[j+1],data_list[j]
print(data_list)
list = [28,32,14,12,53,42]
bubble_sort(list)
三、快速排序
介紹 ? ? ? ?快速排序(Quicksort)是對冒泡排序的一種改進,借用了分治的思想,由C. A. R. Hoare在1962年提出。
基本思想 ? ? ? ?快速排序的基本思想是:挖坑填數(shù) + 分治法。 ? ? ? ?首先選出一個軸值(pivot,也有叫基準的),通過一趟排序?qū)⒋庞涗浄指舫瑟毩⒌膬刹糠郑渲幸徊糠钟涗浀年P(guān)鍵字均比另一部分的關(guān)鍵字小,則可分別對這兩部分記錄繼續(xù)進行排序,以達到整個序列有序。?
實現(xiàn)步驟 ? ? ? ?①從數(shù)列中挑出一個元素,稱為 “基準”(pivot); ? ? ? ?②重新排序數(shù)列,所有元素比基準值小的擺放在基準前面,所有元素比基準值大的擺在基準的后面(相同的數(shù)可以到任一邊); ? ? ? ?③對所有兩個小數(shù)列重復第二步,直至各區(qū)間只有一個數(shù)。
排序演示
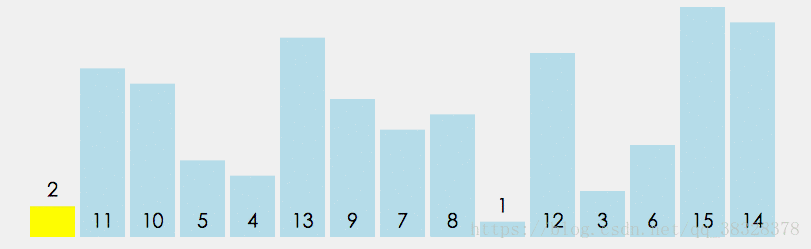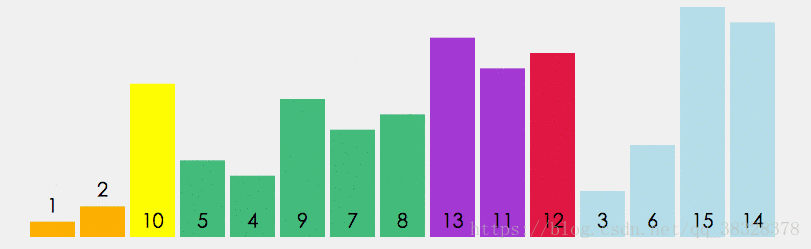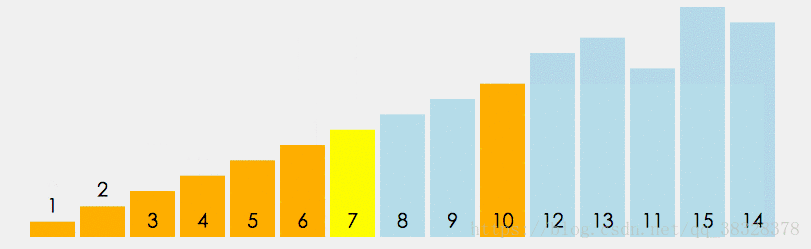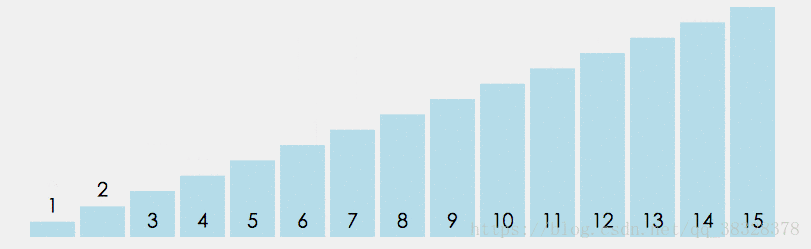
算法實現(xiàn)
#快速排序
def quick_sort(data_list,start,end):
#設置遞歸結(jié)束條件
if start >= end:
return
low_index = start#低位游標
high_index = end #高位游標
basic_data = data_list[start] #初始基準值
while low_index < high_index:
#模擬高位游標從右向左指向的元素與基準值進行比較,比基準值大則高位游標一直向左移動
while low_index < high_index and data_list[high_index] >= basic_data:
high_index -= 1
if low_index != high_index:
#當高位游標指向的元素小于基準值,則移動該值到低位游標指向的位置
data_list[low_index] = data_list[high_index]
low_index += 1 #低位游標向右移動一位
while low_index < high_index and data_list[low_index]<basic_data:
low_index +=1
if low_index != high_index:
data_list[high_index] = data_list[low_index]
high_index -= 1
data_list[low_index] = basic_data
#遞歸調(diào)用
quick_sort(data_list,start,low_index-1) #對基準值左邊未排序隊列排序
quick_sort(data_list,high_index+1,end) #對基準值右邊未排序隊列排序
list = [28,32,14,12,53,42]
quick_sort(list,0,len(list)-1)
print(list)
四、希爾排序
介紹 ? ? ? ?希爾排序(Shell Sort)是插入排序的一種,也是縮小增量排序,是直接插入排序算法的一種更高效的改進版本。希爾排序是非穩(wěn)定排序算法,時間復雜度為:O(1.3n)。
希爾排序是基于插入排序的以下兩點性質(zhì)而提出改進方法的: ? ?·插入排序在對幾乎已經(jīng)排好序的數(shù)據(jù)操作時, 效率高, 即可以達到線性排序的效率; ? ?·但插入排序一般來說是低效的, 因為插入排序每次只能將數(shù)據(jù)移動一位。
基本思想 ? ? ? ①希爾排序是把記錄按下標的一定量分組,對每組使用直接插入算法排序; ? ? ? ②隨著增量逐漸減少,每組包1含的關(guān)鍵詞越來越多,當增量減至1時,整個文件恰被分成一組,算法被終止。
排序演示
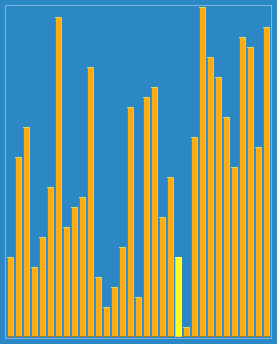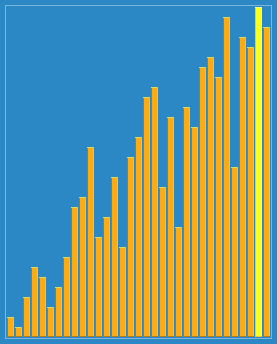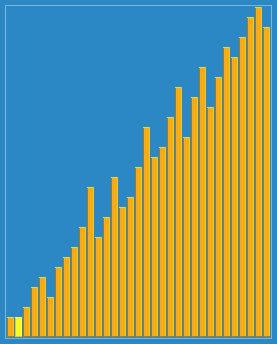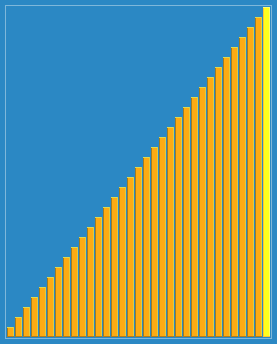
算法實現(xiàn)
# 希爾排序
def shell_sort(lists):
count = len(lists)
step = 2
group = count / step
while group > 0:
for i in range(0, group):
j = i + group
while j < count:
k = j - group
key = lists[j]
while k >= 0:
if lists[k] > key:
lists[k + group] = lists[k]
lists[k] = key
k -= group
j += group
group /= step
return lists
五、選擇排序
介紹 ? ? ? 選擇排序(Selection sort)是一種簡單直觀的排序算法,時間復雜度為Ο(n2)。
基本思想 ? ? ? 選擇排序的基本思想:比較 + 交換。 ? ? ? 第一趟,在待排序記錄r1 ~ r[n]中選出最小的記錄,將它與r1交換; ? ? ? 第二趟,在待排序記錄r2 ~ r[n]中選出最小的記錄,將它與r2交換; ? ? ? 以此類推,第 i?趟,在待排序記錄ri ~ r[n]中選出最小的記錄,將它與r[i]交換,使有序序列不斷增長直到全部排序完畢。
排序演示
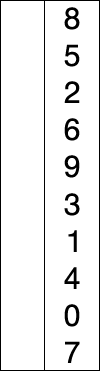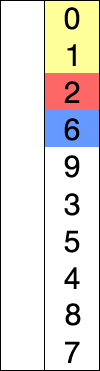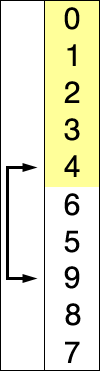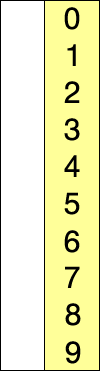
選擇排序的示例動畫。紅色表示當前最小值,黃色表示已排序序列,藍色表示當前位置。?
算法實現(xiàn)
# 選擇排序
def select_sort(lists):
count = len(lists)
for i in range(0, count):
min = i
for j in range(i + 1, count):
if lists[min] > lists[j]:
min = j
lists[min], lists[i] = lists[i], lists[min]
return lists
六、堆排序
介紹
? ? ? ??堆排序(Heapsort)是指利用堆積樹(堆)這種數(shù)據(jù)結(jié)構(gòu)所設計的一種排序算法,它是選擇排序的一種。
????? ? 利用數(shù)組的特點快速指定索引的元素。
基本思想 ? ? ? ?堆分為大根堆和小根堆,是完全二叉樹。 ? ? ? ?大根堆的要求是每個節(jié)點的值不大于其父節(jié)點的值,即A[PARENT[i]] >=A[i]。 ? ? ? ?在數(shù)組的非降序排序中,需要使用的就是大根堆,因為根據(jù)大根堆的要求可知,最大的值一定在堆頂。
排序演示

算法實現(xiàn)
#堆排序
def adjust_heap(lists, i, size):
lchild = 2 * i + 1
rchild = 2 * i + 2
max = i
if i < size / 2:
if lchild < size and lists[lchild] > lists[max]:
max = lchild
if rchild < size and lists[rchild] > lists[max]:
max = rchild
if max != i:
lists[max], lists[i] = lists[i], lists[max]
adjust_heap(lists, max, size)
def build_heap(lists, size):
for i in range(0, (size/2))[::-1]:
adjust_heap(lists, i, size)
def heap_sort(lists):
size = len(lists)
build_heap(lists, size)
for i in range(0, size)[::-1]:
lists[0], lists[i] = lists[i], lists[0]
adjust_heap(lists, 0, i)
七、歸并排序
介紹 ?? ? ? 歸并排序(Merge sort)是建立在歸并操作上的一種有效的排序算法。該算法是采用分治法(Divide and Conquer)的一個非常典型的應用。?
基本思想?? ? ? ? ? 歸并排序算法是將兩個(或兩個以上)有序表合并成一個新的有序表,即把待排序序列分為若干個子序列,每個子序列是有序的。然后再把有序子序列合并為整體有序序列。
算法思想?? ? ? ? ?自上而下遞歸法(假如序列共有n個元素) ? ? ? ? ? ? ① 將序列每相鄰兩個數(shù)字進行歸并操作,形成 floor(n/2)個序列,排序后每個序列包含兩個元素;? ? ? ? ? ? ? ② 將上述序列再次歸并,形成 floor(n/4)個序列,每個序列包含四個元素;? ? ? ? ? ? ? ③ 重復步驟②,直到所有元素排序完畢。?
? ? ? ?自下而上迭代法 ? ? ? ? ? ??① 申請空間,使其大小為兩個已經(jīng)排序序列之和,該空間用來存放合并后的序列; ? ? ? ? ? ? ② 設定兩個指針,最初位置分別為兩個已經(jīng)排序序列的起始位置; ? ? ? ? ? ? ③ 比較兩個指針所指向的元素,選擇相對小的元素放入到合并空間,并移動指針到下一位置; ? ? ? ? ? ? ④ 重復步驟③直到某一指針達到序列尾; ? ? ? ? ? ? ⑤ 將另一序列剩下的所有元素直接復制到合并序列尾。
排序演示

算法實現(xiàn)
# 歸并排序
def merge_sort(data_list):
if len(data_list)<=1:
return data_list
#根據(jù)列表長度確定拆分的中間位置
mid_index = len(data_list) // 2
# left_list = data_list[:mid_index] #使用切片實現(xiàn)對列表的切分
# right_list = data_list[mid_index:]
left_list = merge_sort(data_list[:mid_index])
right_list = merge_sort(data_list[mid_index:])
return merge(left_list,right_list)
def merge(left_list,right_list):
l_index = 0
r_index = 0
merge_list = []
while l_index < len(left_list) and r_index < len(right_list):
if left_list[l_index] < right_list[r_index]:
merge_list.append(left_list[l_index])
l_index += 1
else:
merge_list.append(right_list[r_index])
r_index += 1
merge_list += left_list[l_index:]
merge_list += right_list[r_index:]
return merge_list
list = [28, 32, 14, 12, 53, 42]
new_list = merge_sort(list)
print("--------排序結(jié)果--------")
print(new_list)
八、基數(shù)排序
介紹 ? ? ? 基數(shù)排序(Radix Sort)屬于“分配式排序”,又稱為“桶子法”。 ? ? ? 基數(shù)排序法是屬于穩(wěn)定性的排序,其時間復雜度為O (nlog(r)m)? ,其中 r 為采取的基數(shù),而m為堆數(shù)。 ? ? ??在某些時候,基數(shù)排序法的效率高于其他的穩(wěn)定性排序法。
基本思想 ? ? ? 將所有待比較數(shù)值(正整數(shù))統(tǒng)一為同樣的數(shù)位長度,數(shù)位較短的數(shù)前面補零。然后,從最低位開始,依次進行一次排序。這樣從最低位排序一直到最高位排序完成以后,數(shù)列就變成一個有序序列。
基數(shù)排序按照優(yōu)先從高位或低位來排序有兩種實現(xiàn)方案:
MSD(Most significant digital) 從最左側(cè)高位開始進行排序。先按k1排序分組, 同一組中記錄, 關(guān)鍵碼k1相等,再對各組按k2排序分成子組, 之后, 對后面的關(guān)鍵碼繼續(xù)這樣的排序分組, 直到按最次位關(guān)鍵碼kd對各子組排序后. 再將各組連接起來,便得到一個有序序列。MSD方式適用于位數(shù)多的序列。
LSD (Least significant digital)從最右側(cè)低位開始進行排序。先從kd開始排序,再對kd-1進行排序,依次重復,直到對k1排序后便得到一個有序序列。LSD方式適用于位數(shù)少的序列。 排序效果

算法實現(xiàn)
import math
#基數(shù)排序
def radix_sort(lists, radix=10):
k = int(math.ceil(math.log(max(lists), radix)))
bucket = [[] for i in range(radix)]
for i in range(1, k+1):
for j in lists:
bucket[j/(radix**(i-1)) % (radix**i)].append(j)
del lists[:]
for z in bucket:
lists += z
del z[:]
return lists
九、總結(jié)
各種排序的穩(wěn)定性、時間復雜度、空間復雜度的總結(jié):
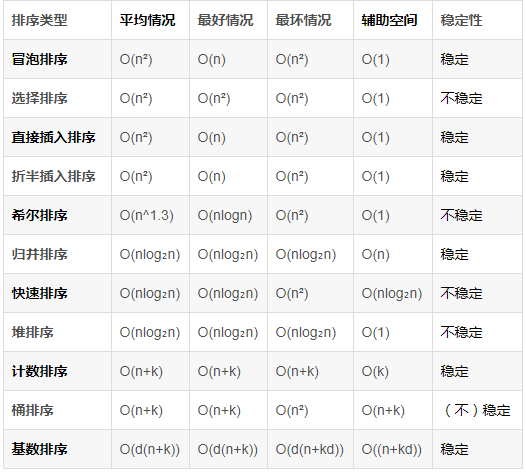
平方階O(n2)排序:各類簡單排序:直接插入、直接選擇和冒泡排序;?
從時間復雜度來說:? 線性對數(shù)階O(nlog?n)排序:快速排序、堆排序和歸并排序;? O(n1+§))排序,§是介于0和1之間的常數(shù):希爾排序?; 線性階O(n)排序:基數(shù)排序,此外還有桶、箱排序。
原文: https://blog.csdn.net/qq_38328378/article/details/85037315
推薦閱讀:《架構(gòu)師離職后,成為自由開發(fā)者的第 100 天》
END
若覺得文章對你有幫助,隨手轉(zhuǎn)發(fā)分享,也是我們繼續(xù)更新的動力。
長按二維碼,掃掃關(guān)注哦
?「C語言中文網(wǎng)」官方公眾號,關(guān)注手機閱讀教程??

點擊“閱讀原文”,領(lǐng)取 2020 年最新免費技術(shù)資料大全
