神經(jīng)網(wǎng)絡(luò)模型在學(xué)術(shù)界和工業(yè)界都處于絕對的壟斷地位，使得「機器學(xué)習(xí)」幾乎要跟「深度學(xué)習(xí)」劃上等號了。

作為深度學(xué)習(xí)的領(lǐng)軍人，吳恩達(dá)自然也是深度學(xué)習(xí)的忠實使用者。

最近吳恩達(dá)在博客網(wǎng)站上發(fā)表了一篇特刊，表示自己由于常年使用神經(jīng)網(wǎng)絡(luò)，已經(jīng)快忘了該怎么用傳統(tǒng)的機器學(xué)習(xí)算法了！

因為深度學(xué)習(xí)并非在所有場景下都好用，所以在「盲目」使用神經(jīng)網(wǎng)絡(luò)受挫后，痛定思痛，寫了一篇文章，為一些傳統(tǒng)的機器學(xué)習(xí)算法提供一些直觀上的解釋。

線性回歸

線性回歸（Linear regression）可能是機器學(xué)習(xí)中的最重要的統(tǒng)計方法，至于誰發(fā)明了這個算法，一直爭論了200年，仍未解決。

1805年，法國數(shù)學(xué)家勒讓德（Adrien-Marie Legendre）在預(yù)測一顆彗星的位置時，發(fā)表了將一條線擬合到一組點上的方法。天體導(dǎo)航是當(dāng)時全球商業(yè)中最有價值的科學(xué)，就像今天的人工智能一樣。

四年后，24歲的德國天才數(shù)學(xué)家高斯（Carl Friedrich Gauss）堅持認(rèn)為，他自1795年以來一直在使用這種方法，但他認(rèn)為這種方法太過瑣碎，無法寫出來。高斯的說法促使Legendre發(fā)表了一份匿名的附錄，指出「一位非常有名的幾何學(xué)家毫不猶豫地采用了這種方法」。

這類長期存在發(fā)明爭議的算法都有兩個特點：好用，且簡單！

線性回歸的本質(zhì)上就是斜率（slopes）和截距（biases，也稱偏置）。

當(dāng)一個結(jié)果和一個影響它的變量之間的關(guān)系是一條直線時，線性回歸就很有用。

例如，一輛汽車的油耗與它的重量呈線性關(guān)系。

一輛汽車的油耗y和它的重量x之間的關(guān)系取決于直線的斜率w（油耗隨重量上升的陡峭程度）和偏置項b（零重量時的油耗）：y=w*x+b。

在訓(xùn)練期間，給定汽車的重量，算法預(yù)測預(yù)期的燃料消耗。它比較了預(yù)期和實際的燃料消耗。然后通過最小二乘法，使平方差最小化，從而修正w和b的值。

考慮到汽車的阻力，有可能產(chǎn)生更精確的預(yù)測。額外的變量將直線延伸到一個平面。通過這種方式，線性回歸可以接收任何數(shù)量的變量/維度作為輸入。

線性回歸算法在當(dāng)年可以幫助航海家追蹤星星，后來幫助生物學(xué)家（特別是查爾斯-達(dá)爾文的表弟弗朗西斯-高爾頓）識別植物和動物的遺傳性狀，進(jìn)一步的發(fā)展釋放了線性回歸的潛力。

1922年，英國統(tǒng)計學(xué)家羅納德-費舍爾和卡爾-皮爾遜展示了線性回歸如何融入相關(guān)和分布的一般統(tǒng)計框架，再次擴大了其適用范圍。

近一個世紀(jì)后，計算機的出現(xiàn)為其提供了數(shù)據(jù)和處理能力，使其得到更大的利用。

當(dāng)然，數(shù)據(jù)從來沒有被完美地測量過，而且多個變量之間也存在不同的重要程度，這些事實也刺激了線性回歸產(chǎn)生了更復(fù)雜的變體。

例如，帶正則化的線性回歸（也稱為嶺回歸）鼓勵線性回歸模型不要過多地依賴任何一個變量，或者說要均勻地依賴最重要的變量。如果你要追求簡化，使用L1的正則化就是lasso回歸，最終的系數(shù)更稀疏。換句話說，它學(xué)會了選擇具有高預(yù)測能力的變量，而忽略了其他的變量。

Elastic net結(jié)合了兩種類型的正則化，當(dāng)數(shù)據(jù)稀少或特征出現(xiàn)關(guān)聯(lián)時，它很有用。

神經(jīng)網(wǎng)絡(luò)中最常見的一種神經(jīng)元就是線性回歸模型，往往后面再跟著一個非線性激活函數(shù)，所以線性回歸是深度學(xué)習(xí)的基本構(gòu)件。

Logistic回歸

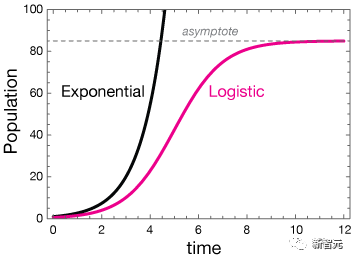
Logistic函數(shù)可以追溯到19世紀(jì)30年代，當(dāng)時比利時統(tǒng)計學(xué)家P.F. Verhulst發(fā)明了該函數(shù)來描述人口動態(tài)。

隨著時間的推移，最初的爆炸性指數(shù)增長在消耗可用資源時趨于平緩，從而形成了Logistic曲線。

一個多世紀(jì)后，美國統(tǒng)計學(xué)家威爾遜（E. B. Wilson）和他的學(xué)生簡-伍斯特（Jane Worcester）設(shè)計了邏輯回歸算法，以計算出多少給定的危險物質(zhì)會致命。

Logistic回歸將logistic函數(shù)擬合到數(shù)據(jù)集上，以預(yù)測在某一事件（例如，攝入馬錢子）發(fā)生特定結(jié)果（例如，過早死亡）的概率。

1、訓(xùn)練時水平地調(diào)整曲線的中心位置，垂直地調(diào)整其中間位置，以使函數(shù)的輸出和數(shù)據(jù)之間的誤差最小。

2、將中心向右或向左調(diào)整意味著需要更多或更少的毒藥來殺死普通人。陡峭的坡度意味著確定性：在中間點之前，大多數(shù)人都能活下來；超過中間點，那就說得再見了。一個平緩的斜率更寬容：低于曲線的中間點，超過一半的人可以存活；更遠(yuǎn)的地方，不到一半。

3、設(shè)置一個閾值，比如說0.5，曲線就成了一個分類器。只要把劑量輸入模型，你就會知道你應(yīng)該計劃一個聚會還是一個葬禮。

Verhulst的工作發(fā)現(xiàn)了二元結(jié)果的概率，后來英國統(tǒng)計學(xué)家David Cox和荷蘭統(tǒng)計學(xué)家Henri Theil在20世紀(jì)60年代末獨立工作，將邏輯回歸法用于有兩個以上類別的情況。

Logistic函數(shù)可以描述多種多樣的現(xiàn)象，并具有相當(dāng)?shù)臏?zhǔn)確性，因此Logistic回歸在許多情況下提供了可用的基線預(yù)測。

在醫(yī)學(xué)上，它可以估計死亡率和疾病的風(fēng)險；在政治中，它可以預(yù)測選舉的贏家和輸家；在經(jīng)濟(jì)學(xué)中，它可以預(yù)測商業(yè)前景。

在神經(jīng)網(wǎng)絡(luò)中，有一部分神經(jīng)元為Logistic回歸，其中非線性函數(shù)為sigmoid。

梯度下降

想象一下，在黃昏過后的山區(qū)徒步旅行，你會發(fā)現(xiàn)除了你的腳以外看不到什么。而你的手機沒電了，所以你無法使用GPS應(yīng)用程序來尋找回家的路。

你可能會發(fā)現(xiàn)梯度下降的方向是最快路徑，只是要小心不要走下懸崖。

1847年，法國數(shù)學(xué)家Augustin-Louis Cauchy發(fā)明了近似恒星軌道的算法。60年后，他的同胞雅克-哈達(dá)瑪?shù)拢↗acques Hadamard）獨立開發(fā)了這一算法，用來描述薄而靈活的物體的變形。

不過，在機器學(xué)習(xí)中，它最常見的用途是找到學(xué)習(xí)算法損失函數(shù)的最低點。

神經(jīng)網(wǎng)絡(luò)通常是一個函數(shù)，給定一個輸入，計算出一個期望的輸出。

訓(xùn)練網(wǎng)絡(luò)的一種方法是，通過反復(fù)計算實際輸出和期望輸出之間的差異，然后改變網(wǎng)絡(luò)的參數(shù)值來縮小該差異，從而使損失最小化，或其輸出中的誤差最小。

梯度下降縮小了誤差，使計算損失的函數(shù)最小化。

網(wǎng)絡(luò)的參數(shù)值相當(dāng)于景觀上的一個位置，而損失是當(dāng)前的高度。隨著你的下降，你提高了網(wǎng)絡(luò)的能力，以計算出接近所需的輸出。

不過可見性是有限的，因為在監(jiān)督學(xué)習(xí)下，算法完全依賴于網(wǎng)絡(luò)的參數(shù)值和梯度，也就是當(dāng)前損失函數(shù)的斜率。

使用梯度下降，你也有可能被困在一個由多個山谷（局部最小值）、山峰（局部最大值）、馬鞍（馬鞍點）和高原組成的非凸形景觀中。事實上，像圖像識別、文本生成和語音識別這樣的任務(wù)都是非凸的，而且已經(jīng)出現(xiàn)了許多梯度下降的變體來處理這種情況。

K-means聚類

如果你在派對上與其他人站得很近，那么你們之間很可能有一些共同點。

K-means的聚類就是基于這種先驗想法，將數(shù)據(jù)點分為多個group，無論這些group是通過人類機構(gòu)還是其他力量形成的，這種算法都會找到它們之間的關(guān)聯(lián)。

美國物理學(xué)家斯圖爾特-勞埃德（Stuart Lloyd）是貝爾實驗室標(biāo)志性創(chuàng)新工廠和發(fā)明原子彈的曼哈頓項目的校友，他在1957年首次提出了k-means聚類，以分配數(shù)字信號中的信息，不過他直到1982年才發(fā)表。

與此同時，美國統(tǒng)計學(xué)家愛德華-福吉（Edward Forgy）在1965年描述了一種類似的方法——勞埃德-福吉算法。

K-means聚類首先會尋找group的中心，然后將數(shù)據(jù)點分配到志同道合的group內(nèi)。考慮到數(shù)據(jù)量在空間里的位置和要組成的小組數(shù)量，k-means聚類可以將與會者分成規(guī)模大致相同的小組，每個小組都聚集在一個中心點或中心點周圍。

在訓(xùn)練過程中，算法最初需要隨機選擇k個人來指定k個中心點，其中k必須手動選擇，而且找到一個最佳的k值并不容易。

然后通過將每個人與最接近的中心點聯(lián)系起來形成k個聚類簇。

對于每個聚類簇，它計算所有被分配到該組的人的平均位置，并將平均位置指定為新的中心點。每個新的中心點可能都不是由一個具體的人占據(jù)的。

在計算出新的中心點后，算法將所有人重新分配到離他們最近的中心點。然后計算新的中心點，調(diào)整集群，以此類推，直到中心點（以及它們周圍的群體）不再移動。

將新人分配到正確的群組很容易，讓他們在房間里找到自己的位置，然后尋找最近的中心點。

K-means算法的原始形式仍然在多個領(lǐng)域很有用，特別是因為作為一種無監(jiān)督的算法，它不需要收集潛在的昂貴的標(biāo)記數(shù)據(jù)，它的運行速度也越來越快。

例如，包括scikit-learn在內(nèi)的機器學(xué)習(xí)庫都得益于2002年增加的kd-trees，它能極快地分割高維數(shù)據(jù)。

參考資料：

整理不易，點贊三連↓