超詳細圖解 Swin Transformer
大家伙,我是DASOU;
之前在B站講解了一下SwinTRM的代碼和論文,今天分享一個很好的文章,從代碼的角度講解論文:
引言
目前Transformer應(yīng)用到圖像領(lǐng)域主要有兩大挑戰(zhàn):
視覺實體變化大,在不同場景下視覺Transformer性能未必很好 圖像分辨率高,像素點多,Transformer基于全局自注意力的計算導(dǎo)致計算量較大
針對上述兩個問題,我們提出了一種包含滑窗操作,具有層級設(shè)計的Swin Transformer。
其中滑窗操作包括不重疊的local window,和重疊的cross-window。將注意力計算限制在一個窗口中,一方面能引入CNN卷積操作的局部性,另一方面能節(jié)省計算量。
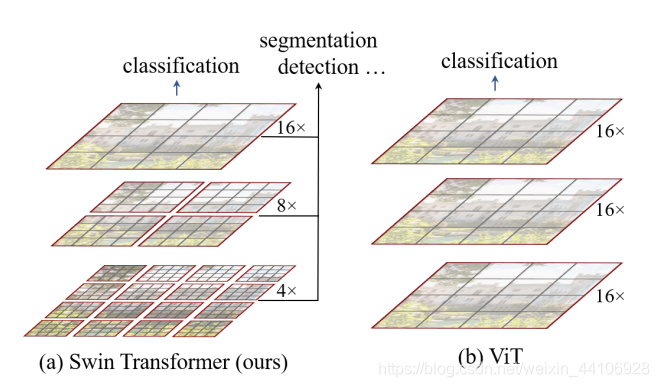
在各大圖像任務(wù)上,Swin Transformer都具有很好的性能。
本文比較長,會根據(jù)官方的開源代碼(https://github.com/microsoft/Swin-Transformer)進行講解,有興趣的可以去閱讀下論文原文(https://arxiv.org/pdf/2103.14030.pdf)。
整體架構(gòu)
我們先看下Swin Transformer的整體架構(gòu)
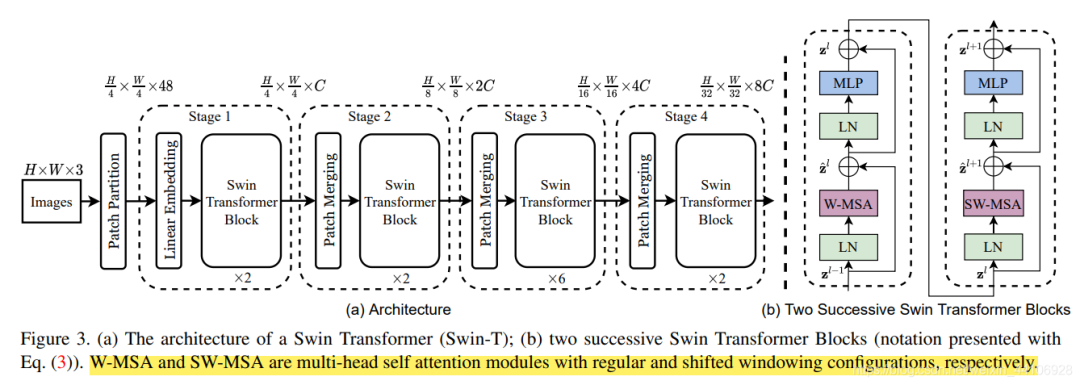
整個模型采取層次化的設(shè)計,一共包含4個Stage,每個stage都會縮小輸入特征圖的分辨率,像CNN一樣逐層擴大感受野。
在輸入開始的時候,做了一個 Patch Embedding,將圖片切成一個個圖塊,并嵌入到Embedding。在每個Stage里,由 Patch Merging和多個Block組成。其中 Patch Merging模塊主要在每個Stage一開始降低圖片分辨率。而Block具體結(jié)構(gòu)如右圖所示,主要是 LayerNorm,MLP,Window Attention和Shifted Window Attention組成 (為了方便講解,我會省略掉一些參數(shù))
class?SwinTransformer(nn.Module):
????def?__init__(...):
????????super().__init__()
????????...
????????#?absolute?position?embedding
????????if?self.ape:
????????????self.absolute_pos_embed?=?nn.Parameter(torch.zeros(1,?num_patches,?embed_dim))
????????????
????????self.pos_drop?=?nn.Dropout(p=drop_rate)
????????#?build?layers
????????self.layers?=?nn.ModuleList()
????????for?i_layer?in?range(self.num_layers):
????????????layer?=?BasicLayer(...)
????????????self.layers.append(layer)
????????self.norm?=?norm_layer(self.num_features)
????????self.avgpool?=?nn.AdaptiveAvgPool1d(1)
????????self.head?=?nn.Linear(self.num_features,?num_classes)?if?num_classes?>?0?else?nn.Identity()
????def?forward_features(self,?x):
????????x?=?self.patch_embed(x)
????????if?self.ape:
????????????x?=?x?+?self.absolute_pos_embed
????????x?=?self.pos_drop(x)
????????for?layer?in?self.layers:
????????????x?=?layer(x)
????????x?=?self.norm(x)??#?B?L?C
????????x?=?self.avgpool(x.transpose(1,?2))??#?B?C?1
????????x?=?torch.flatten(x,?1)
????????return?x
????def?forward(self,?x):
????????x?=?self.forward_features(x)
????????x?=?self.head(x)
????????return?x
其中有幾個地方處理方法與ViT不同:
ViT在輸入會給embedding進行位置編碼。而Swin-T這里則是作為一個可選項( self.ape),Swin-T是在計算Attention的時候做了一個相對位置編碼ViT會單獨加上一個可學習參數(shù),作為分類的token。而Swin-T則是直接做平均,輸出分類,有點類似CNN最后的全局平均池化層
接下來我們看下各個組件的構(gòu)成
Patch Embedding
在輸入進Block前,我們需要將圖片切成一個個patch,然后嵌入向量。
具體做法是對原始圖片裁成一個個 window_size * window_size的窗口大小,然后進行嵌入。
這里可以通過二維卷積層,將stride,kernelsize設(shè)置為window_size大小。設(shè)定輸出通道來確定嵌入向量的大小。最后將H,W維度展開,并移動到第一維度
import?torch
import?torch.nn?as?nn
class?PatchEmbed(nn.Module):
????def?__init__(self,?img_size=224,?patch_size=4,?in_chans=3,?embed_dim=96,?norm_layer=None):
????????super().__init__()
????????img_size?=?to_2tuple(img_size)?#?->?(img_size,?img_size)
????????patch_size?=?to_2tuple(patch_size)?#?->?(patch_size,?patch_size)
????????patches_resolution?=?[img_size[0]?//?patch_size[0],?img_size[1]?//?patch_size[1]]
????????self.img_size?=?img_size
????????self.patch_size?=?patch_size
????????self.patches_resolution?=?patches_resolution
????????self.num_patches?=?patches_resolution[0]?*?patches_resolution[1]
????????self.in_chans?=?in_chans
????????self.embed_dim?=?embed_dim
????????self.proj?=?nn.Conv2d(in_chans,?embed_dim,?kernel_size=patch_size,?stride=patch_size)
????????if?norm_layer?is?not?None:
????????????self.norm?=?norm_layer(embed_dim)
????????else:
????????????self.norm?=?None
????def?forward(self,?x):
????????#?假設(shè)采取默認參數(shù)
????????x?=?self.proj(x)?#?出來的是(N,?96,?224/4,?224/4)?
????????x?=?torch.flatten(x,?2)?#?把HW維展開,(N,?96,?56*56)
????????x?=?torch.transpose(x,?1,?2)??#?把通道維放到最后?(N,?56*56,?96)
????????if?self.norm?is?not?None:
????????????x?=?self.norm(x)
????????return?x
Patch Merging
該模塊的作用是在每個Stage開始前做降采樣,用于縮小分辨率,調(diào)整通道數(shù) 進而形成層次化的設(shè)計,同時也能節(jié)省一定運算量。
在CNN中,則是在每個Stage開始前用
stride=2的卷積/池化層來降低分辨率。
每次降采樣是兩倍,因此在行方向和列方向上,間隔2選取元素。
然后拼接在一起作為一整個張量,最后展開。此時通道維度會變成原先的4倍(因為H,W各縮小2倍),此時再通過一個全連接層再調(diào)整通道維度為原來的兩倍
class?PatchMerging(nn.Module):
????def?__init__(self,?input_resolution,?dim,?norm_layer=nn.LayerNorm):
????????super().__init__()
????????self.input_resolution?=?input_resolution
????????self.dim?=?dim
????????self.reduction?=?nn.Linear(4?*?dim,?2?*?dim,?bias=False)
????????self.norm?=?norm_layer(4?*?dim)
????def?forward(self,?x):
????????"""
????????x:?B,?H*W,?C
????????"""
????????H,?W?=?self.input_resolution
????????B,?L,?C?=?x.shape
????????assert?L?==?H?*?W,?"input?feature?has?wrong?size"
????????assert?H?%?2?==?0?and?W?%?2?==?0,?f"x?size?({H}*{W})?are?not?even."
????????x?=?x.view(B,?H,?W,?C)
????????x0?=?x[:,?0::2,?0::2,?:]??#?B?H/2?W/2?C
????????x1?=?x[:,?1::2,?0::2,?:]??#?B?H/2?W/2?C
????????x2?=?x[:,?0::2,?1::2,?:]??#?B?H/2?W/2?C
????????x3?=?x[:,?1::2,?1::2,?:]??#?B?H/2?W/2?C
????????x?=?torch.cat([x0,?x1,?x2,?x3],?-1)??#?B?H/2?W/2?4*C
????????x?=?x.view(B,?-1,?4?*?C)??#?B?H/2*W/2?4*C
????????x?=?self.norm(x)
????????x?=?self.reduction(x)
????????return?x
下面是一個示意圖(輸入張量N=1, H=W=8, C=1,不包含最后的全連接層調(diào)整)

個人感覺這像是PixelShuffle的反操作
Window Partition/Reverse
window partition函數(shù)是用于對張量劃分窗口,指定窗口大小。將原本的張量從 N H W C, 劃分成 num_windows*B, window_size, window_size, C,其中 num_windows = H*W / window_size,即窗口的個數(shù)。而window reverse函數(shù)則是對應(yīng)的逆過程。這兩個函數(shù)會在后面的Window Attention用到。
def?window_partition(x,?window_size):
????B,?H,?W,?C?=?x.shape
????x?=?x.view(B,?H?//?window_size,?window_size,?W?//?window_size,?window_size,?C)
????windows?=?x.permute(0,?1,?3,?2,?4,?5).contiguous().view(-1,?window_size,?window_size,?C)
????return?windows
def?window_reverse(windows,?window_size,?H,?W):
????B?=?int(windows.shape[0]?/?(H?*?W?/?window_size?/?window_size))
????x?=?windows.view(B,?H?//?window_size,?W?//?window_size,?window_size,?window_size,?-1)
????x?=?x.permute(0,?1,?3,?2,?4,?5).contiguous().view(B,?H,?W,?-1)
????return?x
Window Attention
這是這篇文章的關(guān)鍵。傳統(tǒng)的Transformer都是基于全局來計算注意力的,因此計算復(fù)雜度十分高。而Swin Transformer則將注意力的計算限制在每個窗口內(nèi),進而減少了計算量。
我們先簡單看下公式
主要區(qū)別是在原始計算Attention的公式中的Q,K時加入了相對位置編碼。后續(xù)實驗有證明相對位置編碼的加入提升了模型性能。
class?WindowAttention(nn.Module):
????r"""?Window?based?multi-head?self?attention?(W-MSA)?module?with?relative?position?bias.
????It?supports?both?of?shifted?and?non-shifted?window.
????Args:
????????dim?(int):?Number?of?input?channels.
????????window_size?(tuple[int]):?The?height?and?width?of?the?window.
????????num_heads?(int):?Number?of?attention?heads.
????????qkv_bias?(bool,?optional):??If?True,?add?a?learnable?bias?to?query,?key,?value.?Default:?True
????????qk_scale?(float?|?None,?optional):?Override?default?qk?scale?of?head_dim?**?-0.5?if?set
????????attn_drop?(float,?optional):?Dropout?ratio?of?attention?weight.?Default:?0.0
????????proj_drop?(float,?optional):?Dropout?ratio?of?output.?Default:?0.0
????"""
????def?__init__(self,?dim,?window_size,?num_heads,?qkv_bias=True,?qk_scale=None,?attn_drop=0.,?proj_drop=0.):
????????super().__init__()
????????self.dim?=?dim
????????self.window_size?=?window_size??#?Wh,?Ww
????????self.num_heads?=?num_heads?#?nH
????????head_dim?=?dim?//?num_heads?#?每個注意力頭對應(yīng)的通道數(shù)
????????self.scale?=?qk_scale?or?head_dim?**?-0.5
????????#?define?a?parameter?table?of?relative?position?bias
????????self.relative_position_bias_table?=?nn.Parameter(
????????????torch.zeros((2?*?window_size[0]?-?1)?*?(2?*?window_size[1]?-?1),?num_heads))??#?設(shè)置一個形狀為(2*(Wh-1)?*?2*(Ww-1),?nH)的可學習變量,用于后續(xù)的位置編碼
??
????????self.qkv?=?nn.Linear(dim,?dim?*?3,?bias=qkv_bias)
????????self.attn_drop?=?nn.Dropout(attn_drop)
????????self.proj?=?nn.Linear(dim,?dim)
????????self.proj_drop?=?nn.Dropout(proj_drop)
????????trunc_normal_(self.relative_position_bias_table,?std=.02)
????????self.softmax?=?nn.Softmax(dim=-1)
?????#?相關(guān)位置編碼...
下面我把涉及到相關(guān)位置編碼的邏輯給單獨拿出來,這部分比較繞
首先QK計算出來的Attention張量形狀為(numWindows*B, num_heads, window_size*window_size, window_size*window_size)。
而對于Attention張量來說,以不同元素為原點,其他元素的坐標也是不同的,以window_size=2為例,其相對位置編碼如下圖所示
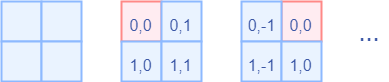
首先我們利用torch.arange和torch.meshgrid函數(shù)生成對應(yīng)的坐標,這里我們以windowsize=2為例子
coords_h?=?torch.arange(self.window_size[0])
coords_w?=?torch.arange(self.window_size[1])
coords?=?torch.meshgrid([coords_h,?coords_w])?#?->?2*(wh,?ww)
"""
??(tensor([[0,?0],
???????????[1,?1]]),?
???tensor([[0,?1],
???????????[0,?1]]))
"""
然后堆疊起來,展開為一個二維向量
coords?=?torch.stack(coords)??#?2,?Wh,?Ww
coords_flatten?=?torch.flatten(coords,?1)??#?2,?Wh*Ww
"""
tensor([[0,?0,?1,?1],
????????[0,?1,?0,?1]])
"""
利用廣播機制,分別在第一維,第二維,插入一個維度,進行廣播相減,得到 2, wh*ww, wh*ww的張量
relative_coords_first?=?coords_flatten[:,?:,?None]??#?2,?wh*ww,?1
relative_coords_second?=?coords_flatten[:,?None,?:]?#?2,?1,?wh*ww
relative_coords?=?relative_coords_first?-?relative_coords_second?#?最終得到?2,?wh*ww,?wh*ww?形狀的張量
因為采取的是相減,所以得到的索引是從負數(shù)開始的,我們加上偏移量,讓其從0開始。
relative_coords?=?relative_coords.permute(1,?2,?0).contiguous()?#?Wh*Ww,?Wh*Ww,?2
relative_coords[:,?:,?0]?+=?self.window_size[0]?-?1
relative_coords[:,?:,?1]?+=?self.window_size[1]?-?1
后續(xù)我們需要將其展開成一維偏移量。而對于(1,2)和(2,1)這兩個坐標。在二維上是不同的,但是通過將x,y坐標相加轉(zhuǎn)換為一維偏移的時候,他的偏移量是相等的。
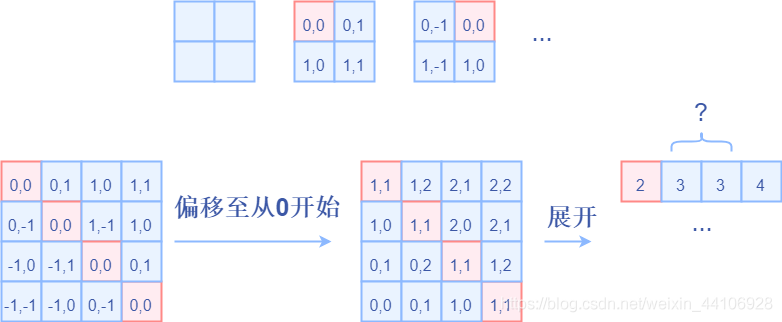
所以最后我們對其中做了個乘法操作,以進行區(qū)分
relative_coords[:,?:,?0]?*=?2?*?self.window_size[1]?-?1

然后再最后一維上進行求和,展開成一個一維坐標,并注冊為一個不參與網(wǎng)絡(luò)學習的變量
relative_position_index?=?relative_coords.sum(-1)??#?Wh*Ww,?Wh*Ww
self.register_buffer("relative_position_index",?relative_position_index)
接著我們看前向代碼
????def?forward(self,?x,?mask=None):
????????"""
????????Args:
????????????x:?input?features?with?shape?of?(num_windows*B,?N,?C)
????????????mask:?(0/-inf)?mask?with?shape?of?(num_windows,?Wh*Ww,?Wh*Ww)?or?None
????????"""
????????B_,?N,?C?=?x.shape
????????
????????qkv?=?self.qkv(x).reshape(B_,?N,?3,?self.num_heads,?C?//?self.num_heads).permute(2,?0,?3,?1,?4)
????????q,?k,?v?=?qkv[0],?qkv[1],?qkv[2]??#?make?torchscript?happy?(cannot?use?tensor?as?tuple)
????????q?=?q?*?self.scale
????????attn?=?(q?@?k.transpose(-2,?-1))
????????relative_position_bias?=?self.relative_position_bias_table[self.relative_position_index.view(-1)].view(
????????????self.window_size[0]?*?self.window_size[1],?self.window_size[0]?*?self.window_size[1],?-1)??#?Wh*Ww,Wh*Ww,nH
????????relative_position_bias?=?relative_position_bias.permute(2,?0,?1).contiguous()??#?nH,?Wh*Ww,?Wh*Ww
????????attn?=?attn?+?relative_position_bias.unsqueeze(0)?#?(1,?num_heads,?windowsize,?windowsize)
????????if?mask?is?not?None:?#?下文會分析到
????????????...
????????else:
????????????attn?=?self.softmax(attn)
????????attn?=?self.attn_drop(attn)
????????x?=?(attn?@?v).transpose(1,?2).reshape(B_,?N,?C)
????????x?=?self.proj(x)
????????x?=?self.proj_drop(x)
????????return?x
首先輸入張量形狀為
numWindows*B, window_size * window_size, C(后續(xù)會解釋)然后經(jīng)過
self.qkv這個全連接層后,進行reshape,調(diào)整軸的順序,得到形狀為3, numWindows*B, num_heads, window_size*window_size, c//num_heads,并分配給q,k,v。根據(jù)公式,我們對
q乘以一個scale縮放系數(shù),然后與k(為了滿足矩陣乘要求,需要將最后兩個維度調(diào)換)進行相乘。得到形狀為(numWindows*B, num_heads, window_size*window_size, window_size*window_size)的attn張量之前我們針對位置編碼設(shè)置了個形狀為
(2*window_size-1*2*window_size-1, numHeads)的可學習變量。我們用計算得到的相對編碼位置索引self.relative_position_index選取,得到形狀為(window_size*window_size, window_size*window_size, numHeads)的編碼,加到attn張量上暫不考慮mask的情況,剩下就是跟transformer一樣的softmax,dropout,與
V矩陣乘,再經(jīng)過一層全連接層和dropout
Shifted Window Attention
前面的Window Attention是在每個窗口下計算注意力的,為了更好的和其他window進行信息交互,Swin Transformer還引入了shifted window操作。
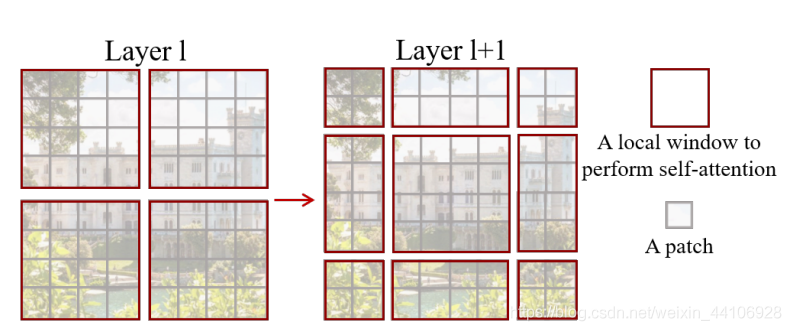
左邊是沒有重疊的Window Attention,而右邊則是將窗口進行移位的Shift Window Attention。可以看到移位后的窗口包含了原本相鄰窗口的元素。但這也引入了一個新問題,即window的個數(shù)翻倍了,由原本四個窗口變成了9個窗口。
在實際代碼里,我們是通過對特征圖移位,并給Attention設(shè)置mask來間接實現(xiàn)的。能在保持原有的window個數(shù)下,最后的計算結(jié)果等價。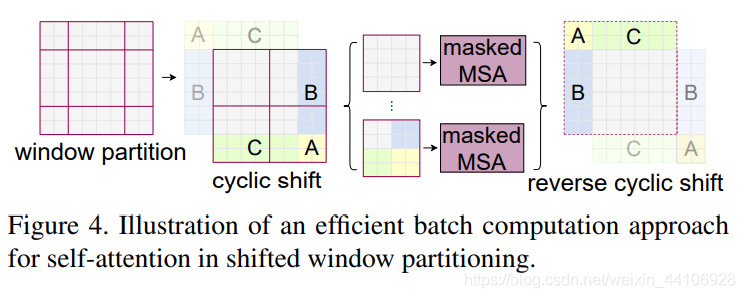
特征圖移位操作
代碼里對特征圖移位是通過torch.roll來實現(xiàn)的,下面是示意圖
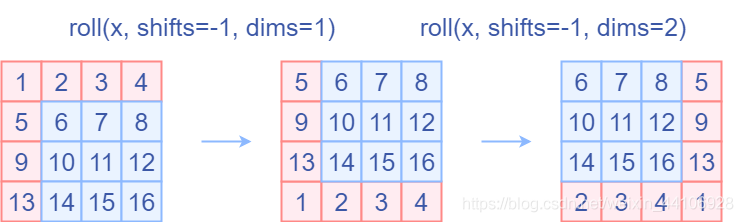
如果需要
reverse cyclic shift的話只需把參數(shù)shifts設(shè)置為對應(yīng)的正數(shù)值。
Attention Mask
我認為這是Swin Transformer的精華,通過設(shè)置合理的mask,讓Shifted Window Attention在與Window Attention相同的窗口個數(shù)下,達到等價的計算結(jié)果。
首先我們對Shift Window后的每個窗口都給上index,并且做一個roll操作(window_size=2, shift_size=1)
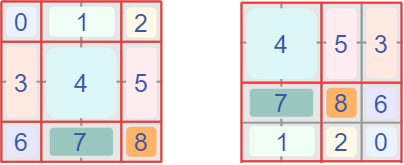
我們希望在計算Attention的時候,讓具有相同index QK進行計算,而忽略不同index QK計算結(jié)果。
最后正確的結(jié)果如下圖所示
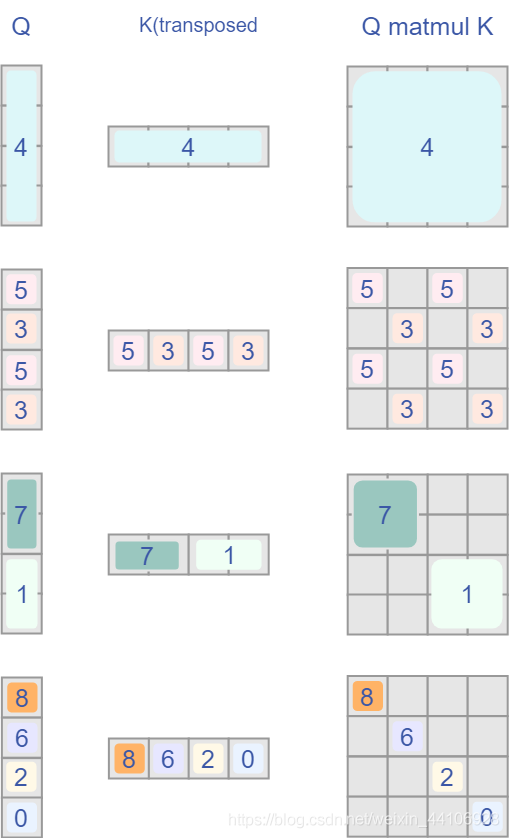
而要想在原始四個窗口下得到正確的結(jié)果,我們就必須給Attention的結(jié)果加入一個mask(如上圖最右邊所示)
相關(guān)代碼如下:
????????if?self.shift_size?>?0:
????????????#?calculate?attention?mask?for?SW-MSA
????????????H,?W?=?self.input_resolution
????????????img_mask?=?torch.zeros((1,?H,?W,?1))??#?1?H?W?1
????????????h_slices?=?(slice(0,?-self.window_size),
????????????????????????slice(-self.window_size,?-self.shift_size),
????????????????????????slice(-self.shift_size,?None))
????????????w_slices?=?(slice(0,?-self.window_size),
????????????????????????slice(-self.window_size,?-self.shift_size),
????????????????????????slice(-self.shift_size,?None))
????????????cnt?=?0
????????????for?h?in?h_slices:
????????????????for?w?in?w_slices:
????????????????????img_mask[:,?h,?w,?:]?=?cnt
????????????????????cnt?+=?1
????????????mask_windows?=?window_partition(img_mask,?self.window_size)??#?nW,?window_size,?window_size,?1
????????????mask_windows?=?mask_windows.view(-1,?self.window_size?*?self.window_size)
????????????attn_mask?=?mask_windows.unsqueeze(1)?-?mask_windows.unsqueeze(2)
????????????attn_mask?=?attn_mask.masked_fill(attn_mask?!=?0,?float(-100.0)).masked_fill(attn_mask?==?0,?float(0.0))
以上圖的設(shè)置,我們用這段代碼會得到這樣的一個mask
tensor([[[[[???0.,????0.,????0.,????0.],
???????????[???0.,????0.,????0.,????0.],
???????????[???0.,????0.,????0.,????0.],
???????????[???0.,????0.,????0.,????0.]]],
?????????[[[???0.,?-100.,????0.,?-100.],
???????????[-100.,????0.,?-100.,????0.],
???????????[???0.,?-100.,????0.,?-100.],
???????????[-100.,????0.,?-100.,????0.]]],
?????????[[[???0.,????0.,?-100.,?-100.],
???????????[???0.,????0.,?-100.,?-100.],
???????????[-100.,?-100.,????0.,????0.],
???????????[-100.,?-100.,????0.,????0.]]],
?????????[[[???0.,?-100.,?-100.,?-100.],
???????????[-100.,????0.,?-100.,?-100.],
???????????[-100.,?-100.,????0.,?-100.],
???????????[-100.,?-100.,?-100.,????0.]]]]])
在之前的window attention模塊的前向代碼里,包含這么一段
????????if?mask?is?not?None:
????????????nW?=?mask.shape[0]
????????????attn?=?attn.view(B_?//?nW,?nW,?self.num_heads,?N,?N)?+?mask.unsqueeze(1).unsqueeze(0)
????????????attn?=?attn.view(-1,?self.num_heads,?N,?N)
????????????attn?=?self.softmax(attn)
將mask加到attention的計算結(jié)果,并進行softmax。mask的值設(shè)置為-100,softmax后就會忽略掉對應(yīng)的值
Transformer Block整體架構(gòu)
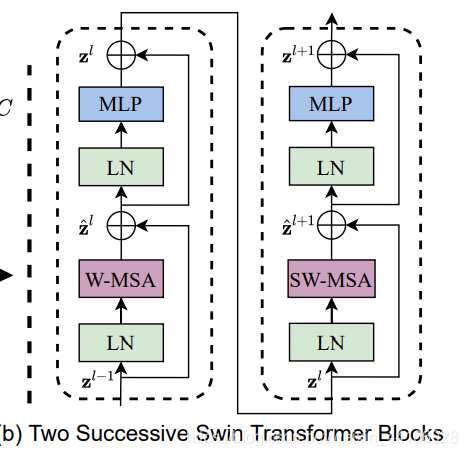
兩個連續(xù)的Block架構(gòu)如上圖所示,需要注意的是一個Stage包含的Block個數(shù)必須是偶數(shù),因為需要交替包含一個含有Window Attention的Layer和含有Shifted Window Attention的Layer。
我們看下Block的前向代碼
????def?forward(self,?x):
????????H,?W?=?self.input_resolution
????????B,?L,?C?=?x.shape
????????assert?L?==?H?*?W,?"input?feature?has?wrong?size"
????????shortcut?=?x
????????x?=?self.norm1(x)
????????x?=?x.view(B,?H,?W,?C)
????????#?cyclic?shift
????????if?self.shift_size?>?0:
????????????shifted_x?=?torch.roll(x,?shifts=(-self.shift_size,?-self.shift_size),?dims=(1,?2))
????????else:
????????????shifted_x?=?x
????????#?partition?windows
????????x_windows?=?window_partition(shifted_x,?self.window_size)??#?nW*B,?window_size,?window_size,?C
????????x_windows?=?x_windows.view(-1,?self.window_size?*?self.window_size,?C)??#?nW*B,?window_size*window_size,?C
????????#?W-MSA/SW-MSA
????????attn_windows?=?self.attn(x_windows,?mask=self.attn_mask)??#?nW*B,?window_size*window_size,?C
????????#?merge?windows
????????attn_windows?=?attn_windows.view(-1,?self.window_size,?self.window_size,?C)
????????shifted_x?=?window_reverse(attn_windows,?self.window_size,?H,?W)??#?B?H'?W'?C
????????#?reverse?cyclic?shift
????????if?self.shift_size?>?0:
????????????x?=?torch.roll(shifted_x,?shifts=(self.shift_size,?self.shift_size),?dims=(1,?2))
????????else:
????????????x?=?shifted_x
????????x?=?x.view(B,?H?*?W,?C)
????????#?FFN
????????x?=?shortcut?+?self.drop_path(x)
????????x?=?x?+?self.drop_path(self.mlp(self.norm2(x)))
????????return?x
整體流程如下
先對特征圖進行LayerNorm 通過 self.shift_size決定是否需要對特征圖進行shift然后將特征圖切成一個個窗口 計算Attention,通過 self.attn_mask來區(qū)分Window Attention還是Shift Window Attention將各個窗口合并回來 如果之前有做shift操作,此時進行 reverse shift,把之前的shift操作恢復(fù)做dropout和殘差連接 再通過一層LayerNorm+全連接層,以及dropout和殘差連接
實驗結(jié)果
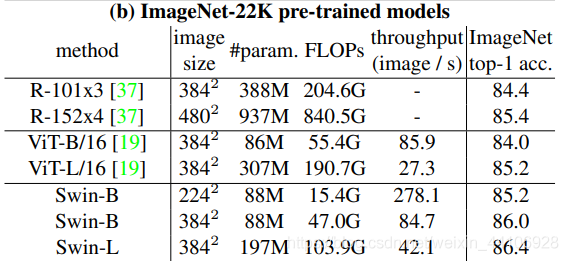
在ImageNet22K數(shù)據(jù)集上,準確率能達到驚人的86.4%。另外在檢測,分割等任務(wù)上表現(xiàn)也很優(yōu)異,感興趣的可以翻看論文最后的實驗部分。
總結(jié)
這篇文章創(chuàng)新點很棒,引入window這一個概念,將CNN的局部性引入,還能控制模型整體計算量。在Shift Window Attention部分,用一個mask和移位操作,很巧妙的實現(xiàn)計算等價。作者的代碼也寫得十分賞心悅目,推薦閱讀!
