重磅!超詳細圖解Self-Attention!
點擊上方“人工智能與算法學習”,選擇“星標★”公眾號
重磅干貨,第一時間送達
Self-Attention 是 Transformer最核心的思想,最近幾日重讀論文,有了一些新的感想。由此寫下本文與讀者共勉。
筆者剛開始接觸Self-Attention時,最大的不理解的地方就是Q K V三個矩陣以及我們常提起的Query查詢向量等等,現(xiàn)在究其原因,應當是被高維繁復的矩陣運算難住了,沒有真正理解矩陣運算的核心意義。因此,在本文開始之前,筆者首先總結(jié)一些基礎(chǔ)知識,文中會重新提及這些知識蘊含的思想是怎樣體現(xiàn)在模型中的。
一些基礎(chǔ)知識
向量的內(nèi)積是什么,如何計算,最重要的,其幾何意義是什么? 一個矩陣 與其自身的轉(zhuǎn)置相乘,得到的結(jié)果有什么意義?
1. 鍵值對注意力
這一節(jié)我們首先分析Transformer中最核心的部分,我們從公式開始,將每一步都繪制成圖,方便讀者理解。
鍵值對Attention最核心的公式如下圖。其實這一個公式中蘊含了很多個點,我們一個一個來講。請讀者跟隨我的思路,從最核心的部分入手,細枝末節(jié)的部分會豁然開朗。
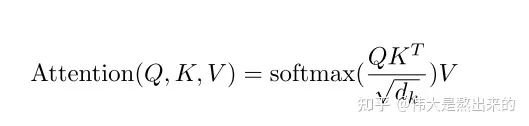
假如上面的公式很難理解,那么下面的公式讀者能否知道其意義是什么呢?
我們先拋開Q K V三個矩陣不談,self-Attention最原始的形態(tài)其實長上面這樣。那么這個公式到底是什么意思呢?
我們一步一步講
代表什么?
一個矩陣乘以它自己的轉(zhuǎn)置,會得到什么結(jié)果,有什么意義?
我們知道,矩陣可以看作由一些向量組成,一個矩陣乘以它自己轉(zhuǎn)置的運算,其實可以看成這些向量分別與其他向量計算內(nèi)積。(此時腦海里想起矩陣乘法的口訣,第一行乘以第一列、第一行乘以第二列......嗯哼,矩陣轉(zhuǎn)置以后第一行不就是第一列嗎?這是在計算第一個行向量與自己的內(nèi)積,第一行乘以第二列是計算第一個行向量與第二個行向量的內(nèi)積第一行乘以第三列是計算第一個行向量與第三個行向量的內(nèi)積.....)
回想我們文章開頭提出的問題,向量的內(nèi)積,其幾何意義是什么?
答:表征兩個向量的夾角,表征一個向量在另一個向量上的投影
記住這個知識點,我們進入一個超級詳細的實例:
我們假設(shè) ,其中 為一個二維矩陣, 為一個行向量(其實很多教材都默認向量是列向量,為了方便舉例請讀者理解筆者使用行向量)。對應下面的圖, 對應"早"字embedding之后的結(jié)果,以此類推。
下面的運算模擬了一個過程,即 。我們來看看其結(jié)果究竟有什么意義
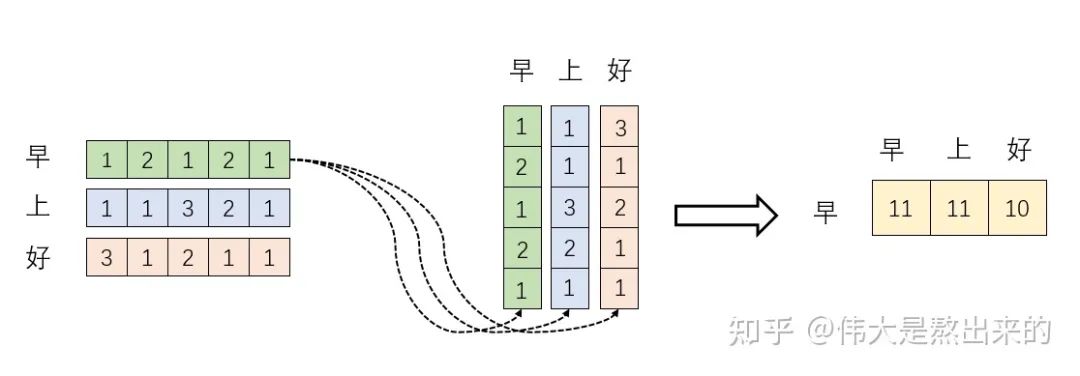
首先,行向量 分別與自己和其他兩個行向量做內(nèi)積("早"分別與"上""好"計算內(nèi)積),得到了一個新的向量。我們回想前文提到的向量的內(nèi)積表征兩個向量的夾角,表征一個向量在另一個向量上的投影。那么新的向量向量有什么意義的?是行向量 在自己和其他兩個行向量上的投影。我們思考,投影的值大有什么意思?投影的值小又如何?
投影的值大,說明兩個向量相關(guān)度高。
我們考慮,如果兩個向量夾角是九十度,那么這兩個向量線性無關(guān),完全沒有相關(guān)性!
更進一步,這個向量是詞向量,是詞在高維空間的數(shù)值映射。詞向量之間相關(guān)度高表示什么?是不是在一定程度上(不是完全)表示,在關(guān)注詞A的時候,應當給予詞B更多的關(guān)注?
上圖展示了一個行向量運算的結(jié)果,那么矩陣 的意義是什么呢?
矩陣 是一個方陣,我們以行向量的角度理解,里面保存了每個向量與自己和其他向量進行內(nèi)積運算的結(jié)果。
至此,我們理解了公式 中, 的意義。我們進一步,Softmax的意義何在呢?請看下圖
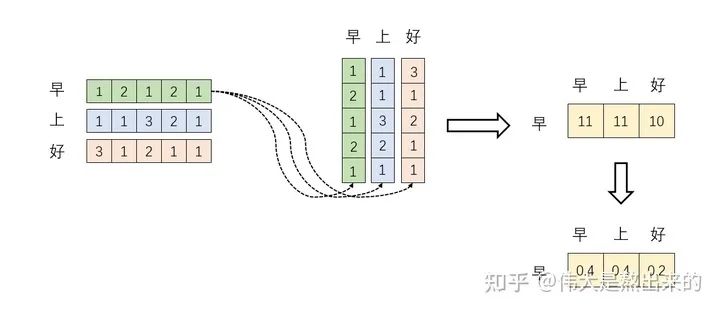
我們回想Softmax的公式,Softmax操作的意義是什么呢?
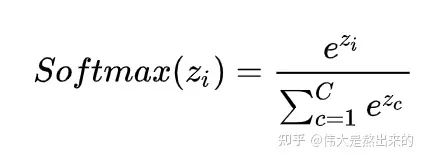
答:歸一化
我們結(jié)合上面圖理解,Softmax之后,這些數(shù)字的和為1了。我們再想,Attention機制的核心是什么?
加權(quán)求和
那么權(quán)重從何而來呢?就是這些歸一化之后的數(shù)字。當我們關(guān)注"早"這個字的時候,我們應當分配0.4的注意力給它本身,剩下0.4關(guān)注"上",0.2關(guān)注"好"。當然具體到我們的Transformer,就是對應向量的運算了,這是后話。
行文至此,我們對這個東西是不是有點熟悉?Python中的熱力圖Heatmap,其中的矩陣是不是也保存了相似度的結(jié)果?
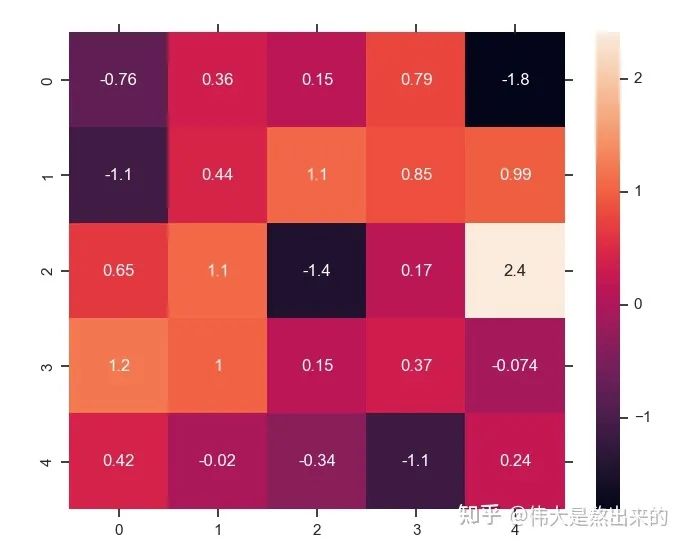
我們仿佛已經(jīng)撥開了一些迷霧,公式 已經(jīng)理解了其中的一半。最后一個 X 有什么意義?完整的公式究竟表示什么?我們繼續(xù)之前的計算,請看下圖
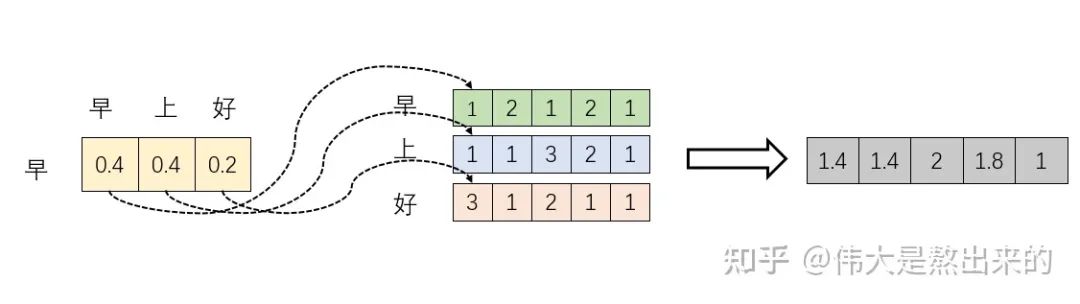
我們?nèi)? 的一個行向量舉例。這一行向量與 的一個列向量相乘,表示什么?
觀察上圖,行向量與 的第一個列向量相乘,得到了一個新的行向量,且這個行向量與 的維度相同。
在新的向量中,每一個維度的數(shù)值都是由三個詞向量在這一維度的數(shù)值加權(quán)求和得來的,這個新的行向量就是"早"字詞向量經(jīng)過注意力機制加權(quán)求和之后的表示。
一張更形象的圖是這樣的,圖中右半部分的顏色深淺,其實就是我們上圖中黃色向量中數(shù)值的大小,意義就是單詞之間的相關(guān)度(回想之前的內(nèi)容,相關(guān)度其本質(zhì)是由向量的內(nèi)積度量的)!
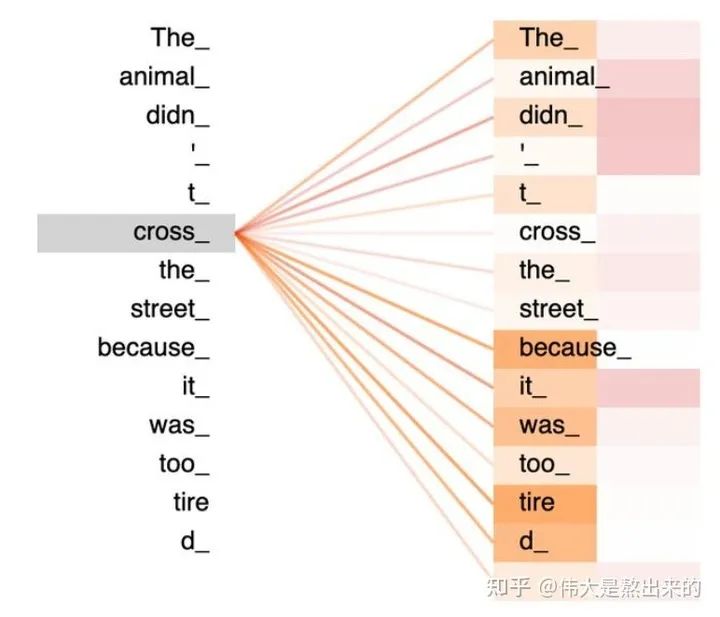
如果您堅持閱讀到這里,相信對公式 已經(jīng)有了更深刻的理解。
我們接下來解釋原始公式中一些細枝末節(jié)的問題
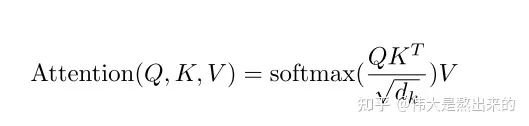
2. Q K V矩陣
在我們之前的例子中并沒有出現(xiàn)Q K V的字眼,因為其并不是公式中最本質(zhì)的內(nèi)容。
Q K V究竟是什么?我們看下面的圖
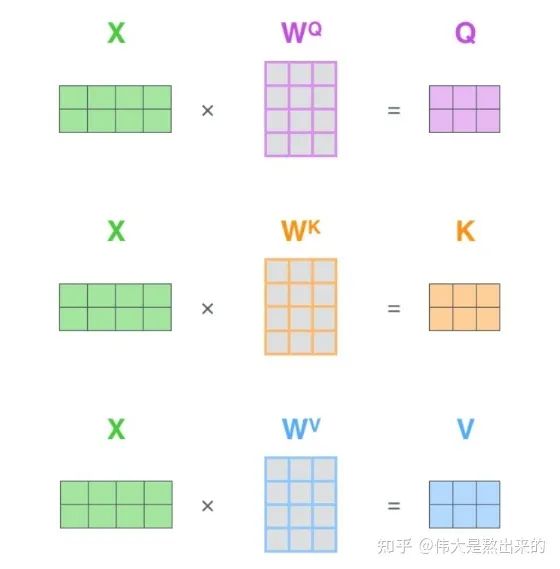
其實,許多文章中所謂的Q K V矩陣、查詢向量之類的字眼,其來源是 與矩陣的乘積,本質(zhì)上都是 的線性變換。
為什么不直接使用 而要對其進行線性變換?
當然是為了提升模型的擬合能力,矩陣 都是可以訓練的,起到一個緩沖的效果。
如果你真正讀懂了前文的內(nèi)容,讀懂了 這個矩陣的意義,相信你也理解了所謂查詢向量一類字眼的含義。
3. 的意義
假設(shè) 里的元素的均值為0,方差為1,那么 中元素的均值為0,方差為d. 當d變得很大時, 中的元素的方差也會變得很大,如果 中的元素方差很大,那么 的分布會趨于陡峭(分布的方差大,分布集中在絕對值大的區(qū)域)。總結(jié)一下就是 的分布會和d有關(guān)。因此 中每一個元素除以 后,方差又變?yōu)?。這使得 的分布“陡峭”程度與d解耦,從而使得訓練過程中梯度值保持穩(wěn)定。
至此Self-Attention中最核心的內(nèi)容已經(jīng)講解完畢,關(guān)于Transformer的更多細節(jié)可以參考我的這篇回答:
最后再補充一點,對self-attention來說,它跟每一個input vector都做attention,所以沒有考慮到input sequence的順序。更通俗來講,大家可以發(fā)現(xiàn)我們前文的計算每一個詞向量都與其他詞向量計算內(nèi)積,得到的結(jié)果丟失了我們原來文本的順序信息。對比來說,LSTM是對于文本順序信息的解釋是輸出詞向量的先后順序,而我們上文的計算對sequence的順序這一部分則完全沒有提及,你打亂詞向量的順序,得到的結(jié)果仍然是相同的。
這就牽扯到Transformer的位置編碼了,我們按住不表。
Self-Attention的代碼實現(xiàn)
# Muti-head Attention 機制的實現(xiàn)
from math import sqrt
import torch
import torch.nn
class Self_Attention(nn.Module):
# input : batch_size * seq_len * input_dim
# q : batch_size * input_dim * dim_k
# k : batch_size * input_dim * dim_k
# v : batch_size * input_dim * dim_v
def __init__(self,input_dim,dim_k,dim_v):
super(Self_Attention,self).__init__()
self.q = nn.Linear(input_dim,dim_k)
self.k = nn.Linear(input_dim,dim_k)
self.v = nn.Linear(input_dim,dim_v)
self._norm_fact = 1 / sqrt(dim_k)
def forward(self,x):
Q = self.q(x) # Q: batch_size * seq_len * dim_k
K = self.k(x) # K: batch_size * seq_len * dim_k
V = self.v(x) # V: batch_size * seq_len * dim_v
atten = nn.Softmax(dim=-1)(torch.bmm(Q,K.permute(0,2,1))) * self._norm_fact # Q * K.T() # batch_size * seq_len * seq_len
output = torch.bmm(atten,V) # Q * K.T() * V # batch_size * seq_len * dim_v
return output

# Muti-head Attention 機制的實現(xiàn)
from math import sqrt
import torch
import torch.nn
class Self_Attention_Muti_Head(nn.Module):
# input : batch_size * seq_len * input_dim
# q : batch_size * input_dim * dim_k
# k : batch_size * input_dim * dim_k
# v : batch_size * input_dim * dim_v
def __init__(self,input_dim,dim_k,dim_v,nums_head):
super(Self_Attention_Muti_Head,self).__init__()
assert dim_k % nums_head == 0
assert dim_v % nums_head == 0
self.q = nn.Linear(input_dim,dim_k)
self.k = nn.Linear(input_dim,dim_k)
self.v = nn.Linear(input_dim,dim_v)
self.nums_head = nums_head
self.dim_k = dim_k
self.dim_v = dim_v
self._norm_fact = 1 / sqrt(dim_k)
def forward(self,x):
Q = self.q(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)
K = self.k(x).reshape(-1,x.shape[0],x.shape[1],self.dim_k // self.nums_head)
V = self.v(x).reshape(-1,x.shape[0],x.shape[1],self.dim_v // self.nums_head)
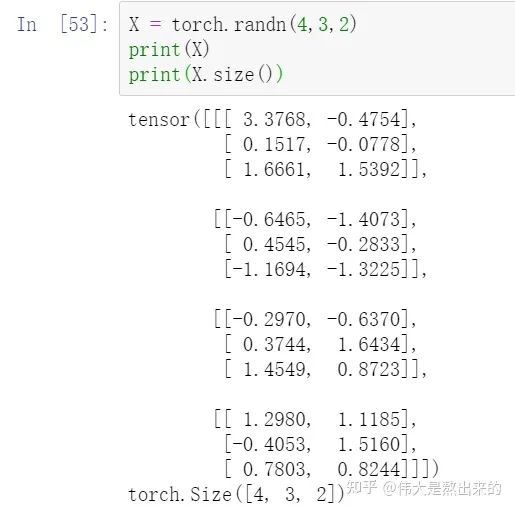
print(x.shape)
print(Q.size())
atten = nn.Softmax(dim=-1)(torch.matmul(Q,K.permute(0,1,3,2))) # Q * K.T() # batch_size * seq_len * seq_len
output = torch.matmul(atten,V).reshape(x.shape[0],x.shape[1],-1) # Q * K.T() * V # batch_size * seq_len * dim_v
return output——The ?End——


