如何判斷算法是否有可優(yōu)化空間?
?【GiantPandaCV導語】計算Armv7a架構理論gflops以及自己寫的某個算法的gflops的方法,另外提供了一個腳本可以顯示native版矩陣乘法各個尺寸對應的gflops。
?
1. 前言
之前一直在寫一些算法怎么優(yōu)化,包括算法邏輯甚至是更加底層一些的文章,但是測試工作都做得比較隨意,也就是粗略的比較時間。最近準備學習一下矩陣乘法的優(yōu)化,覺得這種比較方式實際上是看不出太多信息的,比如不知道當前版本的算法在某塊指定硬件上是否還存在優(yōu)化空間。因此,這篇文章嘗試向大家介紹另外一個算法加速的評判標準,即算法的浮點峰值(gflops)。
?gflops代表計算量除以耗時獲得的值。
?
之前高叔叔發(fā)了一篇文章教會我們如何計算硬件的浮點峰值(https://zhuanlan.zhihu.com/p/28226956),高叔叔的開源代碼是針對x86架構的。然后,我針對移動端(ArmV7-a架構)模仿了一下,在測出硬件的浮點峰值之后,手寫了一個Native版的矩陣乘法并計算這個算法的gflops,以判斷當前版本的算法離達到硬件浮點峰值還有多少優(yōu)化空間。
2. Cortex-A17 硬件浮點峰值計算
詳細原理請查看:浮點峰值那些事 。這里再截取一下計算浮點峰值的操作方法部分:

所以參考這一方法,即可在移動端測出浮點峰值,首先寫出測試的核心代碼實現(xiàn),注意gflops的計算方法就是用計算量除以程序耗時:
#include?
#include?
#define?LOOP?(1e9)
#define?OP_FLOATS?(80)
void?TEST(int);
static?double?get_time(struct?timespec?*start,
???????????????????????struct?timespec?*end)?{
????return?end->tv_sec?-?start->tv_sec?+?(end->tv_nsec?-?start->tv_nsec)?*?1e-9;
}
int?main()?{
????struct?timespec?start,?end;
????double?time_used?=?0.0;
????clock_gettime(CLOCK_MONOTONIC_RAW,?&start);
????TEST(LOOP);
????clock_gettime(CLOCK_MONOTONIC_RAW,?&end);
????time_used?=?get_time(&start,?&end);
????printf("perf:?%.6lf?\r\n",?LOOP?*?OP_FLOATS?*?1.0?*?1e-9?/?time_used);
}
注意這里的TEST是使用了純匯編實現(xiàn),即test.S文件,代碼如下,為什么一次循環(huán)要發(fā)射10條vmla.f32指令,上面截取的計算方法部分講的很清楚,這個地方也可以自己多試幾組值獲得更加精細的硬件FLOPs:
.text
.align?5
.global?TEST
TEST:
.loop2:
????vmla.f32?q0,?q0,?q0
????vmla.f32?q1,?q1,?q1
????vmla.f32?q2,?q2,?q2
????vmla.f32?q3,?q3,?q3
????vmla.f32?q4,?q4,?q4
????vmla.f32?q5,?q5,?q5
????vmla.f32?q6,?q6,?q6
????vmla.f32?q7,?q7,?q7
????vmla.f32?q8,?q8,?q8
????vmla.f32?q9,?q9,?q9
????subs?r0,r0,????#1
????bne?.loop2
我在Cortex-A17上測試了單核的浮點峰值,結果如下:
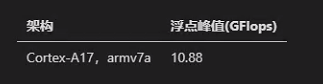
然后大概知道了硬件的浮點峰值,我們在優(yōu)化自己的算法時就至少心中有數(shù)了。
3. 實現(xiàn)Native矩陣乘法,記錄浮點峰值
接著,我們參考https://github.com/flame/how-to-optimize-gemm來實現(xiàn)一個Native版的矩陣乘法,即A矩陣的一行乘以B矩陣的一列獲得C矩陣的一個元素(計算量為2 * M * N * K),并統(tǒng)計它的運算時間以計算gflops,另外為了發(fā)現(xiàn)矩陣乘法的gflops和矩陣尺寸的關系,我們將各個尺寸的矩陣乘法的gflops寫到一個txt文件里面,后面我們使用Python的matplotlib庫把這些數(shù)據畫到一張圖上顯示出來。首先實現(xiàn)不同尺寸的矩陣乘法:
#define?A(?i,?j?)?a[?(i)*lda?+?(j)?]
#define?B(?i,?j?)?b[?(i)*ldb?+?(j)?]
#define?C(?i,?j?)?c[?(i)*ldb?+?(j)?]
//?gemm?C?=?A?*?B?+?C
void?MatrixMultiply(int?m,?int?n,?int?k,?float?*a,?int?lda,?float?*b,?int?ldb,?float?*c,?int?ldc)
{
????for(int?i?=?0;?i?????????for?(int?j=0;?j????????????for?(int?p=0;?p????????????????C(i,?j)?=?C(i,?j)?+?A(i,?p)?*?B(p,?j);
????????????}
????????}
????}
}
測試和統(tǒng)計FLOPs部分的代碼比較長,就貼一點核心部分吧,完整部分可以到github獲取(https://github.com/BBuf/ArmNeonOptimization/tree/master/optimize_gemm):
//?i代表當前矩陣的長寬,長寬都等于i
for(int?i?=?40;?i?<=?800;?i?+=?40){
???????m?=?i;
???????n?=?i;
???????k?=?i;
???????gflops?=?2.0?*?m?*?n?*?k?*?1.0e-09;
???????lda?=?m;
???????ldb?=?n;
???????ldc?=?k;
???????a?=?(float?*)malloc(lda?*?k?*?sizeof(float));
???????b?=?(float?*)malloc(ldb?*?n?*?sizeof(float));
???????c?=?(float?*)malloc(ldc?*?n?*?sizeof(float));
???????prec?=?(float?*)malloc(ldc?*?n?*?sizeof(float));
???????nowc?=?(float?*)malloc(ldc?*?n?*?sizeof(float));
???????//?隨機填充矩陣
???????random_matrix(m,?k,?a,?lda);
???????random_matrix(k,?n,?b,?ldb);
???????random_matrix(m,?n,?prec,?ldc);
???????memset(prec,?0,?ldc?*?n?*?sizeof(float));
???????copy_matrix(m,?n,?prec,?ldc,?nowc,?ldc);
???????//?以nowc為基準,判斷矩陣運行算結果是否正確
???????MatrixMultiply(m,?n,?k,?a,?lda,?b,?ldb,?nowc,?ldc);
???????//?循環(huán)20次,以最快的運行時間為結果
???????for(int?j=0;?j?20;?j++){
???????????
???????????copy_matrix(m,?n,?prec,?ldc,?c,?ldc);
???????????clock_gettime(CLOCK_MONOTONIC_RAW,?&start);
???????????MatrixMultiply(m,?n,?k,?a,?lda,?b,?ldb,?c,?ldc);
???????????clock_gettime(CLOCK_MONOTONIC_RAW,?&end);
???????????time_tmp?=?get_time(&start,?&end);
???????????
???????????if(j?==?0)
???????????????time_best?=?time_tmp;
???????????else
???????????????time_best?=?min(time_best,?time_tmp);
???????}
???????diff?=?compare_matrices(m,?n,?c,?ldc,?nowc,?ldc);
???????if(diff?>?0.5f?||?diff?-0.5f){
???????????exit(0);
???????}
???????printf("%d?%le?%le?\n",?i,?gflops?/?time_best,?diff);
???????fflush(stdout);
???????free(a);
???????free(b);
???????free(c);
???????free(prec);
???????free(nowc);
}
printf("\n");
fflush(stdout);
「在編譯之后運行時只需要新增一個重定向命令,即可獲得記錄了矩陣大小和GFlops的txt文件,例:./unit_test >> now.txt, 注意now.txt需要自己先創(chuàng)建,并保證它有可寫的權限。」
接下來我們使用下面的腳本將now.txt用圖片的方式顯示出來,并將圖片保存到本地:
import?matplotlib.pyplot?as?plt
import?numpy?as?np
def?solve(filename):
????f?=?open(filename)
????sizes?=?[40]
????times?=?[0.0]
????title?=?'origin'
????while?True:
????????line?=?f.readline()
????????if?line:
????????????slices?=?line.split("?")
????????????if?len(slices)?<=?2:
????????????????break;
????????????size?=?int(slices[0])
????????????time?=?float(slices[1])
????????????sizes.append(size)
????????????times.append(time)
????return?title,?sizes,?times
if?__name__?==?'__main__':
????plt.xlabel('size')
????plt.ylabel('gflops')
????t,?x,?y?=?solve('now.txt')
????plt.plot(x,?y,?label=t)
????plt.legend()
????plt.savefig('origin.png')
????plt.show()
我們來看一下結果:
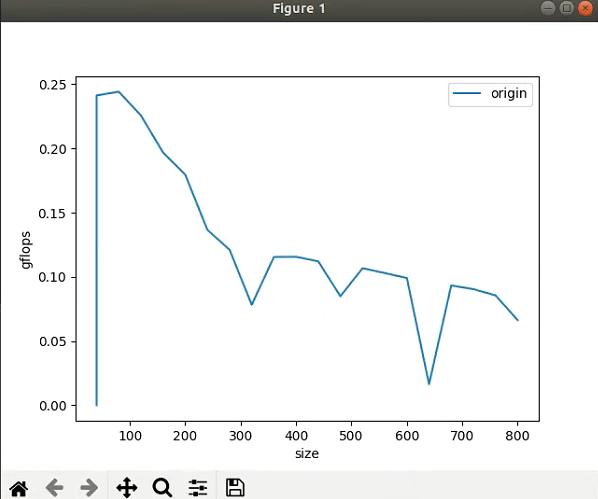
從這張圖可以看到,在矩陣長寬取100的時候可以達到最高的gflops大概是0.25gflops,相對硬件的理論浮點峰值只有2-3%,所以此算法的優(yōu)化空間還是非常巨大的,接下來我們就可以使用如減少乘法次數(shù),內存對齊,分塊等策略去改進這個算法獲得更好的gflops。這樣,我們在算法優(yōu)化的過程中就可以更加直觀的看到算法的性能。
4. 小結
這篇文章只是矩陣優(yōu)化部分的開篇,主要是受到高叔叔的文章啟發(fā)給對移動端或者PC端感興趣的同學提供一個gflops的計算實例,并提供一個將gflops更加直觀顯示的腳本工具,希望對大家有用。
5. 參考
https://zhuanlan.zhihu.com/p/65436463 https://zhuanlan.zhihu.com/p/28226956 https://github.com/flame/how-to-optimize-gemm
歡迎關注GiantPandaCV, 在這里你將看到獨家的深度學習分享,堅持原創(chuàng),每天分享我們學習到的新鮮知識。( ? ?ω?? )?
有對文章相關的問題,或者想要加入交流群,歡迎添加BBuf微信:
為了方便讀者獲取資料以及我們公眾號的作者發(fā)布一些Github工程的更新,我們成立了一個QQ群,二維碼如下,感興趣可以加入。
