用 Python 神經(jīng)網(wǎng)絡預測汽車保險支出
↑↑↑關注后"星標"簡說Python 人人都可以簡單入門Python、爬蟲、數(shù)據(jù)分析 簡說Python推薦 來源/Python中文社區(qū) 作者/沂水寒城

如何加載和匯總?cè)鸬淦嚤kU數(shù)據(jù)集,以及如何使用結(jié)果建議要使用的數(shù)據(jù)準備和模型配置。 如何探索簡單的MLP模型的學習動態(tài)以及數(shù)據(jù)集上的數(shù)據(jù)轉(zhuǎn)換。 如何開發(fā)出對模型性能的可靠估計,調(diào)整模型性能以及對新數(shù)據(jù)進行預測。
汽車保險回歸數(shù)據(jù)集 首個MLP和學習動力 評估和調(diào)整MLP模型 最終模型和做出預測
汽車保險數(shù)據(jù)集( auto-insurance.csv)汽車保險數(shù)據(jù)集詳細信息( auto-insurance.names)
108,392.5
19,46.2
13,15.7
124,422.2
40,119.4
# load the dataset and summarize the shape
from pandas import read_csv
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
# load the dataset
df = read_csv(url, header=None)
# summarize shape
print(df.shape)
(63, 2)
# show summary statistics and plots of the dataset
from pandas import read_csv
from matplotlib import pyplot
# define the location of the dataset
url = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
# load the dataset
df = read_csv(url, header=None)
# show summary statistics
print(df.describe())
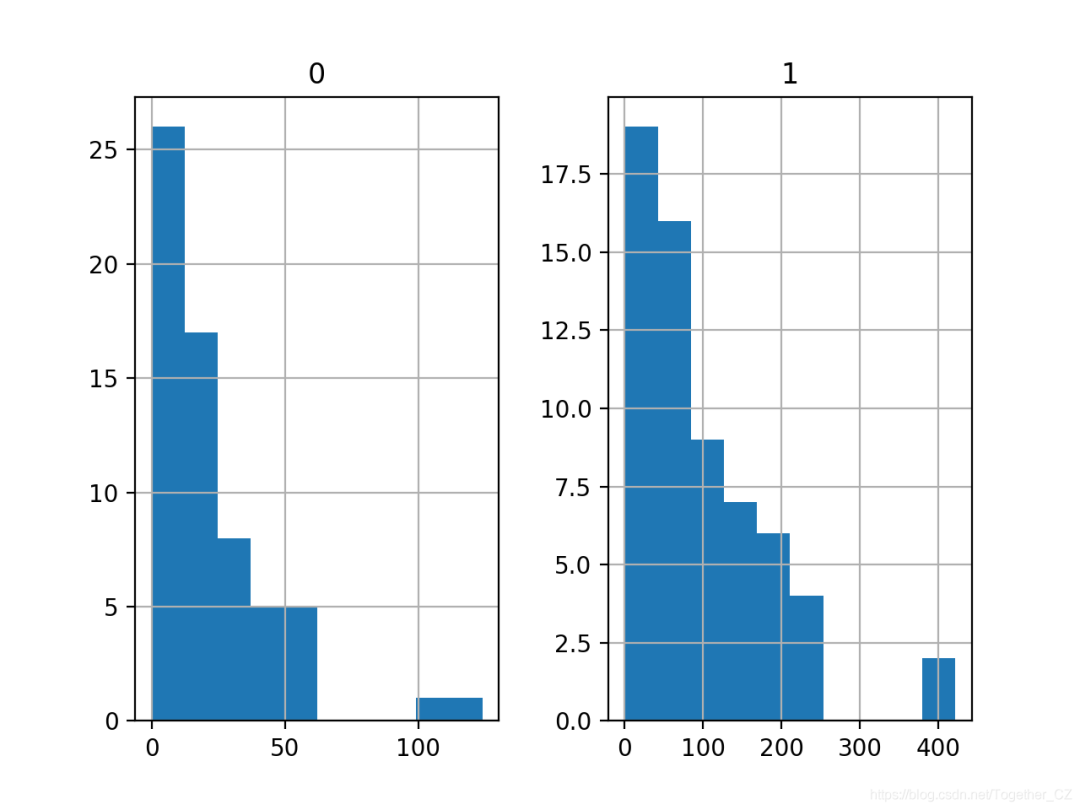
# plot histograms
df.hist()
pyplot.show()
0 1
count 63.000000 63.000000
mean 22.904762 98.187302
std 23.351946 87.327553
min 0.000000 0.000000
25% 7.500000 38.850000
50% 14.000000 73.400000
75% 29.000000 140.000000
max 124.000000 422.200000
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
# fit a simple mlp model and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
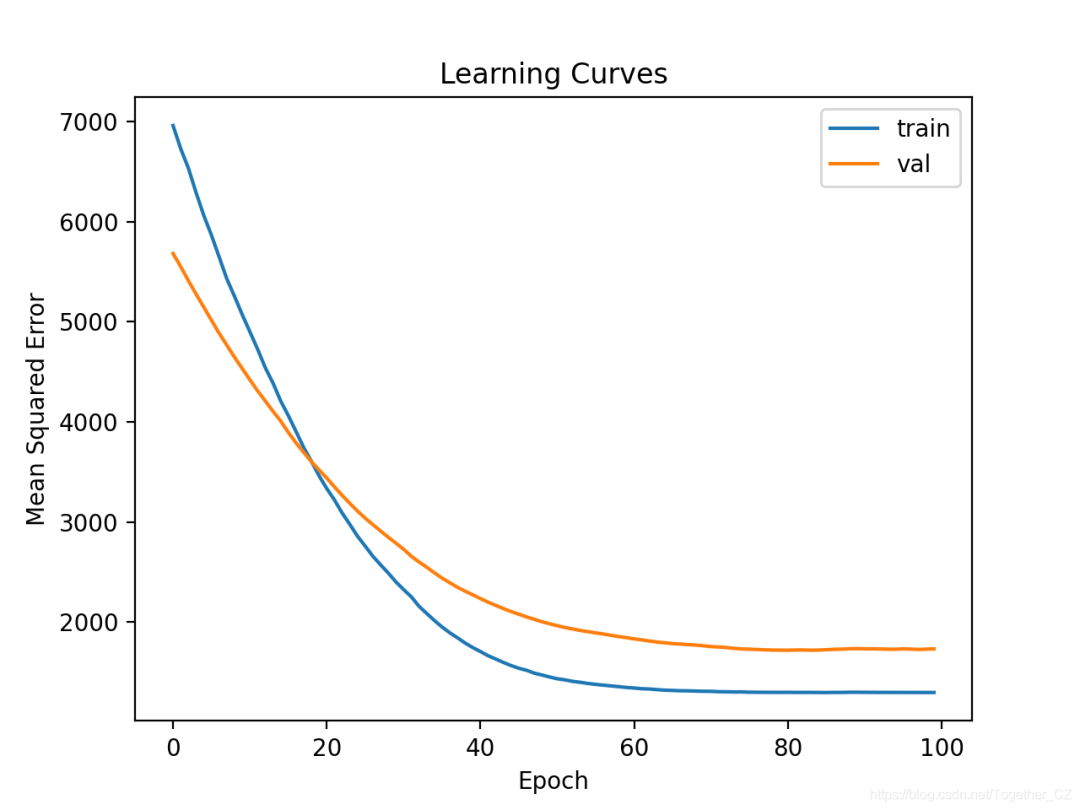
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
MAE: 33.233
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# fit a deeper mlp model and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
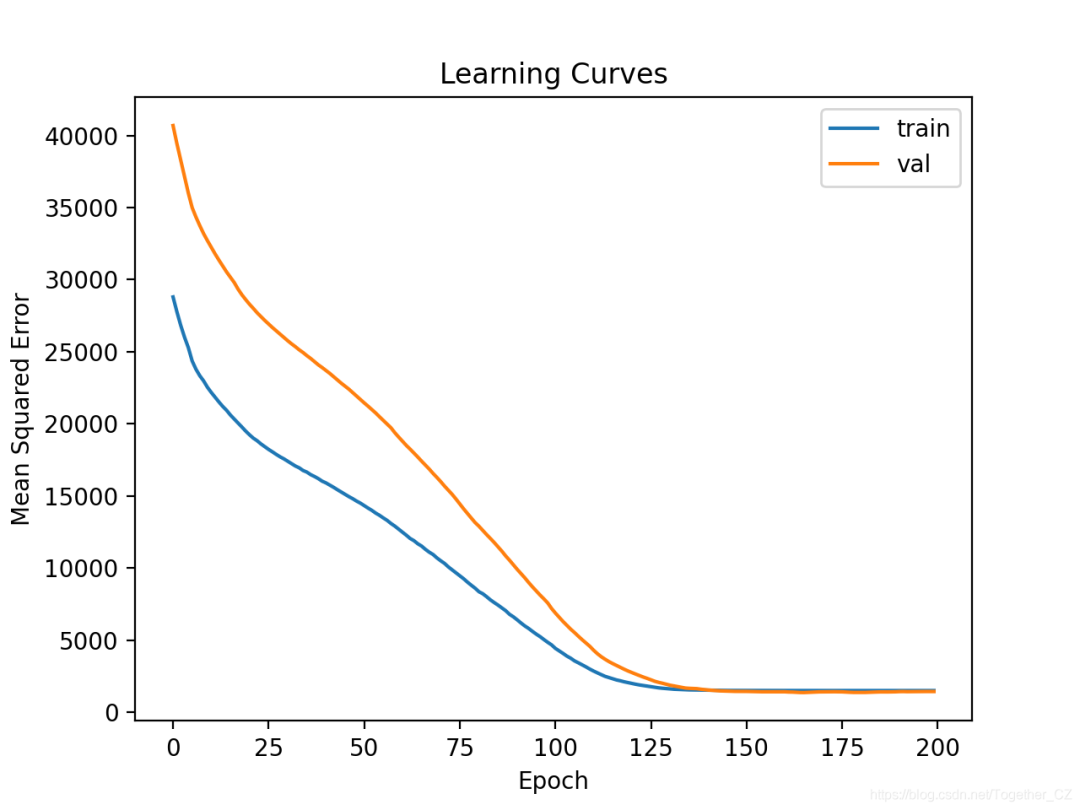
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
MAE: 27.939
# ensure that the target variable is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# power transform input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# power transform output data
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# inverse transforms on target variable
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# fit a mlp model with data transforms and review learning curves
from pandas import read_csv
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import PowerTransformer
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# split into train and test datasets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)
# ensure that the target variable is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# power transform input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# power transform output data
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
history = model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0, validation_data=(X_test,y_test))
# predict test set
yhat = model.predict(X_test)
# inverse transforms on target variable
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('MAE: %.3f' % score)
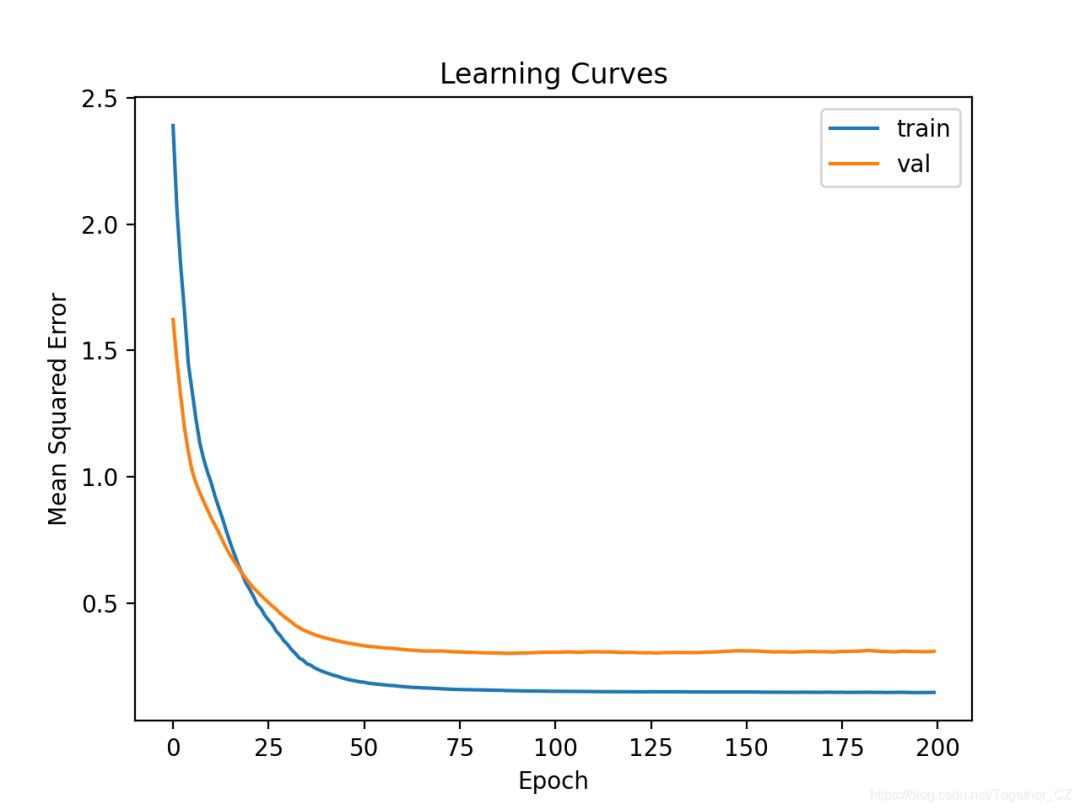
# plot learning curves
pyplot.title('Learning Curves')
pyplot.xlabel('Epoch')
pyplot.ylabel('Mean Squared Error')
pyplot.plot(history.history['loss'], label='train')
pyplot.plot(history.history['val_loss'], label='val')
pyplot.legend()
pyplot.show()
MAE: 34.320
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# fit and evaluate the model...
...
...
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
# k-fold cross-validation of base model for the auto insurance regression dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=100, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
>27.314
>69.577
>20.891
>14.810
>13.412
>69.540
>25.612
>49.508
>35.769
>62.696
Mean MAE: 38.913 (21.056)
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# k-fold cross-validation of deeper model for the auto insurance regression dataset
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
Mean MAE: 35.384 (14.951)
# k-fold cross-validation of deeper model with data transforms
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import PowerTransformer
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# ensure target is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# prepare input data
pt1 = PowerTransformer()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = PowerTransformer()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# inverse transforms
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
Mean MAE: 37.371 (29.326)
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# k-fold cross-validation of deeper model with normalization transforms
from numpy import mean
from numpy import std
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
from matplotlib import pyplot
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# prepare cross validation
kfold = KFold(10)
# enumerate splits
scores = list()
for train_ix, test_ix in kfold.split(X, y):
# split data
X_train, X_test, y_train, y_test = X[train_ix], X[test_ix], y[train_ix], y[test_ix]
# ensure target is a 2d array
y_train, y_test = y_train.reshape((len(y_train),1)), y_test.reshape((len(y_test),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X_train)
X_train = pt1.transform(X_train)
X_test = pt1.transform(X_test)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y_train)
y_train = pt2.transform(y_train)
y_test = pt2.transform(y_test)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X_train, y_train, epochs=200, batch_size=8, verbose=0)
# predict test set
yhat = model.predict(X_test)
# inverse transforms
y_test = pt2.inverse_transform(y_test)
yhat = pt2.inverse_transform(yhat)
# evaluate predictions
score = mean_absolute_error(y_test, yhat)
print('>%.3f' % score)
scores.append(score)
# summarize all scores
print('Mean MAE: %.3f (%.3f)' % (mean(scores), std(scores)))
Mean MAE: 30.388 (14.258)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure target is a 2d array
y = y.reshape((len(y),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X)
X = pt1.transform(X)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y)
y = pt2.transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# define a row of new data
row = [13]
# transform the input data
X_new = pt1.transform([row])
# make prediction
yhat = model.predict(X_new)
# invert transform on prediction
yhat = pt2.inverse_transform(yhat)
# report prediction
print('f(%s) = %.3f' % (row, yhat[0]))
# fit a final model and make predictions on new data.
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.metrics import mean_absolute_error
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras import Sequential
from tensorflow.keras.layers import Dense
# load the dataset
path = 'https://raw.githubusercontent.com/jbrownlee/Datasets/master/auto-insurance.csv'
df = read_csv(path, header=None)
# split into input and output columns
X, y = df.values[:, :-1], df.values[:, -1]
# ensure target is a 2d array
y = y.reshape((len(y),1))
# prepare input data
pt1 = MinMaxScaler()
pt1.fit(X)
X = pt1.transform(X)
# prepare target
pt2 = MinMaxScaler()
pt2.fit(y)
y = pt2.transform(y)
# determine the number of input features
n_features = X.shape[1]
# define model
model = Sequential()
model.add(Dense(10, activation='relu', kernel_initializer='he_normal', input_shape=(n_features,)))
model.add(Dense(8, activation='relu', kernel_initializer='he_normal'))
model.add(Dense(1))
# compile the model
model.compile(optimizer='adam', loss='mse')
# fit the model
model.fit(X, y, epochs=200, batch_size=8, verbose=0)
# define a row of new data
row = [13]
# transform the input data
X_new = pt1.transform([row])
# make prediction
yhat = model.predict(X_new)
# invert transform on prediction
yhat = pt2.inverse_transform(yhat)
# report prediction
print('f(%s) = %.3f' % (row, yhat[0]))
f([13]) = 62.595
作者:沂水寒城,CSDN博客專家,個人研究方向:機器學習、深度學習、NLP、CV
Blog: http://yishuihancheng.blog.csdn.net
掃碼回復:2021
即可獲取最新Python學習資源
學習更多: 整理了我開始分享學習筆記到現(xiàn)在超過250篇優(yōu)質(zhì)文章,涵蓋數(shù)據(jù)分析、爬蟲、機器學習等方面,別再說不知道該從哪開始,實戰(zhàn)哪里找了
看完“點贊”的美德不能丟 
評論
圖片
表情
