用Python實現(xiàn)神經(jīng)網(wǎng)絡(luò)（附完整代碼）！

在學(xué)習神經(jīng)網(wǎng)絡(luò)之前，我們需要對神經(jīng)網(wǎng)絡(luò)底層先做一個基本的了解。我們將在本節(jié)介紹感知機、反向傳播算法以及多種梯度下降法以給大家一個全面的認識。

數(shù)字感知機的本質(zhì)是從數(shù)據(jù)集中選取一個樣本（example），并將其展示給算法，然后讓算法判斷“是”或“不是”。一般而言，把單個特征表示為xi，其中i是整數(shù)。所有特征的集合表示為，表示一個向量：，

類似地，每個特征的權(quán)重表示為? 其中? 對應(yīng)于與該權(quán)重關(guān)聯(lián)的特征的下標，所有權(quán)重可統(tǒng)一表示為 一個向量:

這里有一個缺少的部分是是否激活神經(jīng)元的閾值。一旦加權(quán)和超過某個閾值，感知機就輸出1，否則輸出0。我們可以使用一個簡單的階躍函數(shù)（在圖5-2中標記為“激活函數(shù)”）來表示這個閾值。

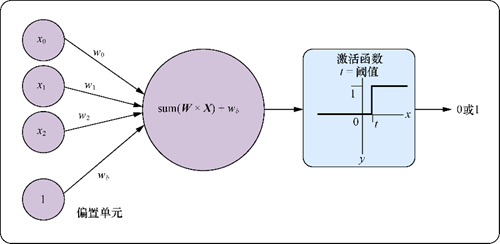
一般而言我們還需要給上面的閾值表達式添加一個偏置項以確保神經(jīng)元對全0的輸入具有彈性，否則網(wǎng)絡(luò)在輸入全為0的情況下輸出仍然為0。

注：所有神經(jīng)網(wǎng)絡(luò)的基本單位都是神經(jīng)元，基本感知機是廣義神經(jīng)元的一個特例，從現(xiàn)在開始，我們將感知機稱為一個神經(jīng)元。

2.1 代價函數(shù)

很多數(shù)據(jù)值之間的關(guān)系不是線性的，也沒有好的線性回歸或線性方程能夠描述這些關(guān)系。許多數(shù)據(jù)集不能用直線或平面來線性分割。比如下圖中左圖為線性可分的數(shù)據(jù)，而右圖為線性不可分的數(shù)據(jù)：

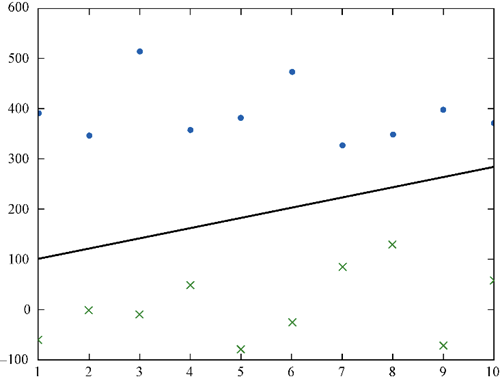
在這個線性可分數(shù)據(jù)集上對兩類點做切分得到的誤差可以收斂于0，而對于線性不可分的數(shù)據(jù)點集，我們無法做出一條直線使得兩類點被完美分開，因此我們?nèi)我庾鲆粭l分割線，可以認為在這里誤差不為0，因此我們需要一個衡量誤差的函數(shù)，通常稱之為代價函數(shù)：

而我們訓(xùn)練神經(jīng)網(wǎng)絡(luò)（感知機）的目標是最小化所有輸入樣本數(shù)據(jù)的代價函數(shù)

2.2 反向傳播

權(quán)重通過下一層的權(quán)重（）和（）來影響誤差，因此我們需要一種方法來計算對誤差的貢獻，這個方法就是反向傳播。

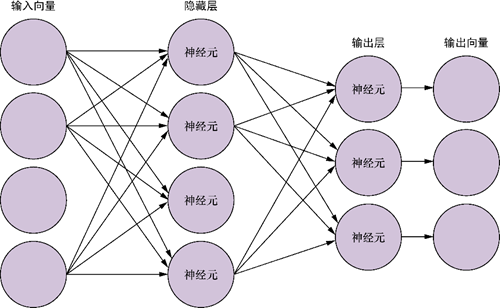
下圖中展示的是一個全連接網(wǎng)絡(luò)，圖中沒有展示出所有的連接，在全連接網(wǎng)絡(luò)中，每個輸入元素都與下一層的各個神經(jīng)元相連，每個連接都有相應(yīng)的權(quán)重。因此，在一個以四維向量為輸入、有5個神經(jīng)元的全連接神經(jīng)網(wǎng)絡(luò)中，一共有20個權(quán)重（5個神經(jīng)元各連接4個權(quán)重）。

感知機的每個輸入都有一個權(quán)重，第二層神經(jīng)元的權(quán)重不是分配給原始輸入的，而是分配給來自第一層的各個輸出。從這里我們可以看到計算第一層權(quán)重對總體誤差的影響的難度。第一層權(quán)重對誤差的影響并不是只來自某個單獨權(quán)重，而是通過下一層中每個神經(jīng)元的權(quán)重來產(chǎn)生的。反向傳播的推導(dǎo)過程較為復(fù)雜，這里僅簡單展示其結(jié)果：

如果該層是輸出層，借助于可微的激活函數(shù)，權(quán)重的更新比較簡單, 對于第? 個輸出，誤差的導(dǎo)數(shù)如下

如果要更新隱藏層的權(quán)重，則會稍微復(fù)雜一點兒：

函數(shù)表示實際結(jié)果向量，表示該向量第個位置上的值，，是倒數(shù)第二層第個節(jié)點和輸出第個節(jié)點的輸出，連接這兩個節(jié)點的權(quán)重為，誤差代價函數(shù)對求導(dǎo)的結(jié)果相當于用（學(xué)習率）乘以前一層的輸出再乘以后一層代價函數(shù)的導(dǎo)數(shù)。公式中表示層第個節(jié)點上的誤差項，前一層第個節(jié)點到層所有的節(jié)點進行加權(quán)求和。

2.3 多種梯度下降法

到目前為止，我們一直是把所有訓(xùn)練樣本的誤差聚合起來然后再做梯度下降，這種訓(xùn)練方法稱為批量學(xué)習（batch learning）。一批是訓(xùn)練數(shù)據(jù)的一個子集。但是在批量學(xué)習中誤差曲面對于整個批是靜態(tài)的，如果從一個隨機的起始點開始，得到的很可能是某個局部極小值，從而無法看到其他的權(quán)重值的更優(yōu)解。這里有兩種方法來避開這個陷阱。

第一種方法是隨機梯度下降法。在隨機梯度下降中，不用去查看所有的訓(xùn)練樣本，而是在輸入每個訓(xùn)練樣本后就去更新網(wǎng)絡(luò)權(quán)重。在這個過程中，每次都會重新排列訓(xùn)練樣本的順序，這樣將為每個樣本重新繪制誤差曲面，由于每個相異的輸入都可能有不同的預(yù)期答案，因此大多數(shù)樣本的誤差曲面都不一樣。對每個樣本來說，仍然使用梯度下降法來調(diào)整權(quán)重。不過不用像之前那樣在每個訓(xùn)練周期結(jié)束后聚合所有誤差再做權(quán)重調(diào)整，而是針對每個樣本都會去更新一次權(quán)重。其中的關(guān)鍵點是，每一步都在向假定的極小值前進（不是所有路徑都通往假定的極小值）。

使用正確的數(shù)據(jù)和超參數(shù)，在向這個波動誤差曲面的各個最小值前進時，可以更容易地得到全局極小值。如果模型沒有進行適當?shù)恼{(diào)優(yōu)，或者訓(xùn)練數(shù)據(jù)不一致，將導(dǎo)致原地踏步，模型無法收斂，也學(xué)不會任何東西。不過在實際應(yīng)用中，隨機梯度下降法在大多數(shù)情況下都能有效地避免局部極小值。這種方法的缺點是計算速度比較慢。計算前向傳播和反向傳播，然后針對每個樣本進行權(quán)重更新，這在本來已經(jīng)很慢的計算過程的基礎(chǔ)上又增加了很多時間開銷。

第二種方法，也是更常見的方法，是小批量學(xué)習。在小批量學(xué)習中，會傳入訓(xùn)練集的一個小的子集，并按照批量學(xué)習中的誤差聚合方法對這個子集對應(yīng)的誤差進行聚合。然后對每個子集按批將其誤差進行反向傳播并更新權(quán)重。下一批會重復(fù)這個過程，直到訓(xùn)練集處理完成為止，這就重新構(gòu)成了一個訓(xùn)練周期。這是一種折中的辦法，它同時具有批量學(xué)習（快速）和隨機梯度下降（具有彈性）的優(yōu)點。

用原生Python來編寫神經(jīng)網(wǎng)絡(luò)是一個非常有趣的嘗試，而且可以幫助大家理解神經(jīng)網(wǎng)絡(luò)中的各種概念，但是Python在計算速度上有明顯缺陷，即使對于中等規(guī)模的網(wǎng)絡(luò)，計算量也會變得非常棘手。不過有許多Python庫可以用來提高運算速度，包括PyTorch、Theano、TensorFlow和Lasagne等。本書中的例子使用Keras。

Keras是一個高級封裝器，封裝了面向Python的API。API接口可以與3個不同的后端庫相兼容：Theano、谷歌的TensorFlow和微軟的CNTK。這幾個庫都在底層實現(xiàn)了基本的神經(jīng)網(wǎng)絡(luò)單元和高度優(yōu)化的線性代數(shù)庫，可以用于處理點積，以支持高效的神經(jīng)網(wǎng)絡(luò)矩陣乘法運算。

我們以簡單的異或問題為例，看看如何用Keras來訓(xùn)練這個網(wǎng)絡(luò)。

import numpy as np
from keras.models import Sequential　　# Kera的基礎(chǔ)模型類
from keras.layers import Dense, Activation　　# Dense是神經(jīng)元的全連接層
from keras.optimizers import SGD　　# 隨機梯度下降，Keras中還有一些其他優(yōu)化器
# Our examples for an exclusive OR.
x_train = np.array([[0, 0],
                    [0, 1],
                    [1, 0],
                    [1, 1]]) 　　# x_train是二維特征向量表示的訓(xùn)練樣本列表
y_train = np.array([[0],
                    [1],
                    [1],
                    [0]]) 　　# y_train是每個特征向量樣本對應(yīng)的目標輸出值
model = Sequential()
num_neurons = 10　　#　全連接隱藏層包含10個神經(jīng)元
model.add(Dense(num_neurons, input_dim=2)) 　　#　 input_dim僅在第一層中使用，后面的其他層會自動計算前一層輸出的形狀，這個例子中輸入的XOR樣本是二維特征向量，因此input_dim設(shè)置為2
model.add(Activation('tanh'))
model.add(Dense(1)) 　　#　輸出層包含一個神經(jīng)元，輸出結(jié)果是二分類值（0或1）
model.add(Activation('sigmoid'))
model.summary()

可以看到模型的結(jié)構(gòu)為：

Layer (type)                 Output Shape                Param 
=================================================================
dense_18 (Dense)             (None, 10)                  30
_________________________________________________________________
activation_6 (Activation)    (None, 10)                  0
_________________________________________________________________
dense_19 (Dense)             (None, 1)                   11
_________________________________________________________________
activation_7 (Activation)    (None, 1)                   0
=================================================================
Total params: 41.0
Trainable params: 41.0
Non-trainable params: 0.0

model.summary()提供了網(wǎng)絡(luò)參數(shù)及各階段權(quán)重數(shù)（Param \#）的概覽。我們可以快速計算一下：10個神經(jīng)元，每個神經(jīng)元有3個權(quán)重，其中有兩個是輸入向量的權(quán)重（輸入向量中的每個值對應(yīng)一個權(quán)重），還有一個是偏置對應(yīng)的權(quán)重，所以一共有30個權(quán)重需要學(xué)習。輸出層中有10個權(quán)重，分別與第一層的10個神經(jīng)元一一對應(yīng)，再加上1個偏置權(quán)重，所以該層共有11個權(quán)重。

下面的代碼可能有點兒不容易理解：

sgd = SGD(lr=0.1)
model.compile(loss='binary_crossentropy', optimizer=sgd, metrics=['accuracy'])

SGD是之前導(dǎo)入的隨機梯度下降優(yōu)化器，模型用它來最小化誤差或者損失。lr是學(xué)習速率，與每個權(quán)重的誤差的導(dǎo)數(shù)結(jié)合使用，數(shù)值越大模型的學(xué)習速度越快，但可能會使模型無法找到全局極小值，數(shù)值越小越精確，但會增加訓(xùn)練時間，并使模型更容易陷入局部極小值。損失函數(shù)本身也定義為一個參數(shù)，在這里用的是binary_crossentropy。metrics參數(shù)是訓(xùn)練過程中輸出流的選項列表。用compile方法進行編譯，此時還未開始訓(xùn)練模型，只對權(quán)重進行了初始化，大家也可以嘗試一下用這個隨機初始狀態(tài)來預(yù)測，當然得到的結(jié)果只是隨機猜測：

model.predict(x_train)
[[ 0.5       ]
 [ 0.43494844]
 [ 0.50295198]
 [ 0.42517585]]

predict方法將給出最后一層的原始輸出，在這個例子中是由sigmoid函數(shù)生成的。

之后再沒什么好寫的了，但是這里還沒有關(guān)于答案的任何知識，它只是對輸入使用了隨機權(quán)重。接下來可以試著進行訓(xùn)練。

model.fit(x_train, y_train, epochs=100) 　　#　從這里開始訓(xùn)練模型
Epoch 1/100
4/4 [==============================] - 0s - loss: 0.6917 - acc: 0.7500
Epoch 2/100
4/4 [==============================] - 0s - loss: 0.6911 - acc: 0.5000
Epoch 3/100
4/4 [==============================] - 0s - loss: 0.6906 - acc: 0.5000
...
Epoch 100/100
4/4 [==============================] - 0s - loss: 0.6661 - acc: 1.0000

在第一次訓(xùn)練時網(wǎng)絡(luò)可能不會收斂。第一次編譯可能以隨機分布的參數(shù)結(jié)束，導(dǎo)致難以或者不能得到全局極小值。如果遇到這種情況，可以用相同的參數(shù)再次調(diào)用model.fit，或者添加更多訓(xùn)練周期，看看網(wǎng)絡(luò)能否收斂。或者也可以用不同的隨機起始點來重新初始化網(wǎng)絡(luò)，然后再次嘗試fit。如果使用后面這種方法，請確保沒有設(shè)置隨機種子，否則只會不斷重復(fù)同樣的實驗結(jié)果。

當網(wǎng)絡(luò)一遍又一遍地學(xué)習這個小數(shù)據(jù)集時，它終于弄明白了這是怎么回事。它從樣本中“學(xué)會”了什么是異或！這就是神經(jīng)網(wǎng)絡(luò)的神奇之處。

model.predict_classes(x_train)
4/4 [==============================] - 0s
[[0]
 [1]
 [1]
 [0]]
model.predict(x_train)
4/4 [==============================] - 0s
[[ 0.0035659 ]
 [ 0.99123639]
 [ 0.99285167]
 [ 0.00907462]]

在這個經(jīng)過訓(xùn)練的模型上再次調(diào)用predict（和predict_classes）會產(chǎn)生更好的結(jié)果。它在這個小數(shù)據(jù)集上獲得了 100%的精確度。當然，精確率并不是評估預(yù)測模型的最佳標準，但對這個小例子來說完全可以說明問題。接下來展示了如何保存這個異或模型:

import h5py
model_structure = model.to_json()　　#　用Keras的輔助方法將網(wǎng)絡(luò)結(jié)構(gòu)導(dǎo)出為JSON blob類型以備后用

with open("basic_model.json", "w") as json_file:
	json_file.write(model_structure)

model.save_weights("basic_weights.h5")　　#　訓(xùn)練好的權(quán)重必須被單獨保存。第一部分只保存網(wǎng)絡(luò)結(jié)構(gòu)。在后面重新加載網(wǎng)絡(luò)結(jié)構(gòu)時必須對其重新實例化

同樣也有對應(yīng)的方法來重新實例化模型，這樣做預(yù)測時不必再去重新訓(xùn)練模型。雖然運行這個模型只需要幾秒，但是在后面的章節(jié)中，模型的運行時間將會快速增長到以分鐘、小時甚至天為單位，這取決于硬件性能和模型的復(fù)雜度，所以請準備好！