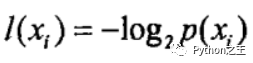數(shù)據(jù)分析及算法總結(jié)
一. K-近鄰算
工作原理
簡(jiǎn)潔的講: 如果一個(gè)樣本在特定的空間中的K個(gè)最鄰近的中的大多數(shù)屬于某個(gè)類,則這個(gè)樣本屬于這個(gè)類.
用途
k近鄰的目的是測(cè)量不同特征值與數(shù)據(jù)集之間的距離來(lái)進(jìn)行分類
樣本差異性
歐式距離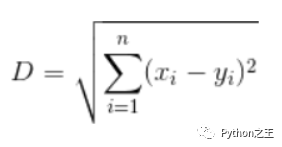
優(yōu)缺點(diǎn)
優(yōu)點(diǎn):精度高、對(duì)異常值不敏感、無(wú)數(shù)據(jù)輸入假定。缺點(diǎn):時(shí)間復(fù)雜度高、空間復(fù)雜度高。適用數(shù)據(jù)范圍:數(shù)值型和標(biāo)稱型。
導(dǎo)包
分類問(wèn)題:from sklearn.neighbors import KNeighborsClassifier 1. ?回歸問(wèn)題:from sklearn.neighbors import KNeighborsRegressor
參數(shù)
n_neighbors:取鄰近點(diǎn)的個(gè)數(shù)k。k取1-9測(cè)試- weight:距離的權(quán)重;uniform:一致的權(quán)重;distance:距離的倒數(shù)作為權(quán)重- p:閔可斯基距離的p值; p=1:即歐式距離;p=2:即曼哈頓距離;p取1-6測(cè)試
二、線性回歸
【關(guān)鍵詞】最小二乘法,線性
原理
普通的線性回歸
最小二乘法
平方誤差可以寫(xiě)做:
對(duì)W求導(dǎo),當(dāng)導(dǎo)數(shù)為零時(shí),平方誤差最小,此時(shí)W等于: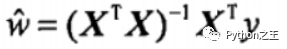
導(dǎo)包
from sklearn.linear_model import LinearRegression
嶺回歸
嶺回歸是加了二階正則項(xiàng)(lambda*I)的最小二乘,主要適用于過(guò)擬合嚴(yán)重或各變量之間存在多重共線性的時(shí)候,嶺回歸是有bias的,這里的bias是為了讓variance更小。
為了得到一致假設(shè)而使假設(shè)變得過(guò)度嚴(yán)格稱為過(guò)擬合,
bias:指的是模型在樣本上的輸出與真實(shí)值的誤差 variance:指的是每個(gè)模型的輸出結(jié)果與所有模型平均值(期望)之間的誤差
公式
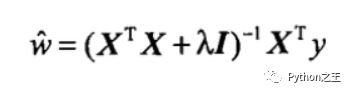
導(dǎo)包
from sklearn.linear_model import Ridge
參數(shù)
alpha:調(diào)整為大于1的數(shù)字
優(yōu)點(diǎn)
縮減方法可以去掉不重要的參數(shù),因此能更好地理解數(shù)據(jù)。此外,與簡(jiǎn)單的線性回歸相比,縮減法能取得更好的預(yù)測(cè)效果 2. 嶺回歸是加了二階正則項(xiàng)的最小二乘,主要適用于過(guò)擬合嚴(yán)重或各變量之間存在多重共線性的時(shí)候,嶺回歸是有bias的,這里的bias是為了讓variance更小。
歸納總結(jié)
嶺回歸可以解決特征數(shù)量比樣本量多的問(wèn)題1. 嶺回歸作為一種縮減算法可以判斷哪些特征重要或者不重要,有點(diǎn)類似于降維的效果1. 縮減算法可以看作是對(duì)一個(gè)模型增加偏差的同時(shí)減少方差
嶺回歸用于處理下面兩類問(wèn)題:
數(shù)據(jù)點(diǎn)少于變量個(gè)數(shù)1. 變量間存在共線性(最小二乘回歸得到的系數(shù)不穩(wěn)定,方差很大)
lasso回歸
原理
【拉格朗日乘數(shù)法】
對(duì)于參數(shù)w增加一個(gè)限定條件,能到達(dá)和嶺回歸一樣的效果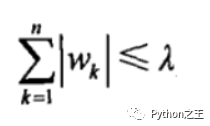
在lambda足夠小的時(shí)候,一些系數(shù)會(huì)因此被迫縮減到0
導(dǎo)包
from sklearn.linear_model import Lasso
參數(shù):
alpha:調(diào)整為小于1的數(shù)字
三、邏輯斯蒂回歸(分類)
【關(guān)鍵詞】Logistics函數(shù),最大似然估計(jì),梯度下降法
Logistics回歸的原理
利用Logistics回歸進(jìn)行分類的主要思想是:根據(jù)現(xiàn)有數(shù)據(jù)對(duì)分類邊界線建立回歸公式,以此進(jìn)行分類。這里的“回歸” 一詞源于最佳擬合,表示要找到最佳擬合參數(shù)集。
預(yù)測(cè)函數(shù)
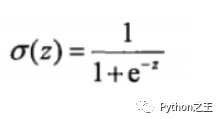
Cost函數(shù)
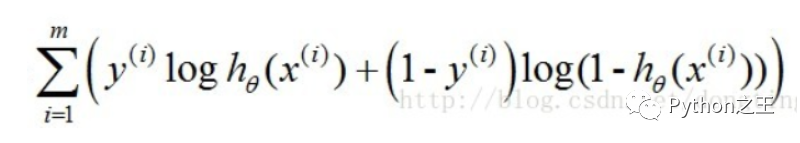
梯度下降法求J(θ)的最小值
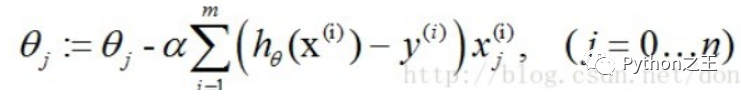
訓(xùn)練分類器時(shí)的做法就是尋找最佳擬合參數(shù),使用的是最優(yōu)化算法。接下來(lái)介紹這個(gè)二值型輸出分類器的數(shù)學(xué)原理
Logistic Regression和Linear Regression的原理是相似的,可以簡(jiǎn)單的描述為這樣的過(guò)程:
找一個(gè)合適的預(yù)測(cè)函數(shù),一般表示為h函數(shù),該函數(shù)就是我們需要找的分類函數(shù),它用來(lái)預(yù)測(cè)輸入數(shù)據(jù)的判斷結(jié)果1. 構(gòu)造一個(gè)Cost函數(shù)(損失函數(shù)),該函數(shù)表示預(yù)測(cè)的輸出(h)與訓(xùn)練數(shù)據(jù)類別(y)之間的偏差,可以是二者之間的差(h-y)或者是其他的形式 。綜合考慮所有訓(xùn)練數(shù)據(jù)的“損失”,將Cost求和或者求平均,記為J(θ)函數(shù),表示所有訓(xùn)練數(shù)據(jù)預(yù)測(cè)值與實(shí)際類別的偏差。1. 顯然,J(θ)函數(shù)的值越小表示預(yù)測(cè)函數(shù)越準(zhǔn)確(即h函數(shù)越準(zhǔn)確),所以這一步需要做的是找到J(θ)函數(shù)的最小值
參數(shù)
solver參數(shù)的選擇:
“l(fā)iblinear”:小數(shù)量級(jí)的數(shù)據(jù)集- “l(fā)bfgs”, “sag” or “newton-cg”:大數(shù)量級(jí)的數(shù)據(jù)集以及多分類問(wèn)題- “sag”:極大的數(shù)據(jù)集
優(yōu)缺點(diǎn)
優(yōu)點(diǎn): 實(shí)現(xiàn)簡(jiǎn)單,易于理解和實(shí)現(xiàn);計(jì)算代價(jià)不高,速度很快,存儲(chǔ)資源低
缺點(diǎn): 容易欠擬合,分類精度可能不高
四、決策樹(shù)
【關(guān)鍵詞】樹(shù),信息增益
構(gòu)造
信息論
不同于邏輯斯蒂回歸和貝葉斯算法,決策樹(shù)的構(gòu)造過(guò)程不依賴領(lǐng)域知識(shí),它使用屬性選擇度量來(lái)選擇將元組最好地劃分成不同的類的屬性。所謂決策樹(shù)的構(gòu)造就是進(jìn)行屬性選擇度量確定各個(gè)特征屬性之間的拓?fù)浣Y(jié)構(gòu)。
構(gòu)造決策樹(shù)的關(guān)鍵步驟是分裂屬性。所謂分裂屬性就是在某個(gè)節(jié)點(diǎn)處按照某一特征屬性的不同劃分構(gòu)造不同的分支,其目標(biāo)是讓各個(gè)分裂子集盡可能地“純”。盡可能“純”就是盡量讓一個(gè)分裂子集中待分類項(xiàng)屬于同一類別。分裂屬性分為三種不同的情況:
? 1、屬性是離散值且不要求生成二叉決策樹(shù)。此時(shí)用屬性的每一個(gè)劃分作為一個(gè)分支。
? 2、屬性是離散值且要求生成二叉決策樹(shù)。此時(shí)使用屬性劃分的一個(gè)子集進(jìn)行測(cè)試,按照“屬于此子集”和“不屬于此子集”分成兩個(gè)分支。
? 3、屬性是連續(xù)值。此時(shí)確定一個(gè)值作為分裂點(diǎn)split_point,按照>split_point和<=split_point生成兩個(gè)分支。
構(gòu)造決策樹(shù)的關(guān)鍵性內(nèi)容是進(jìn)行屬性選擇度量,屬性選擇度量是一種選擇分裂準(zhǔn)則,它決定了拓?fù)浣Y(jié)構(gòu)及分裂點(diǎn)split_point的選擇。
屬性選擇度量算法有很多,一般使用自頂向下遞歸分治法,并采用不回溯的貪心策略。這里介紹常用的ID3算法。
ID3算法
劃分?jǐn)?shù)據(jù)集的大原則是:將無(wú)序的數(shù)據(jù)變得更加有序
原理
決策樹(shù)(decision tree)是一個(gè)樹(shù)結(jié)構(gòu)(可以是二叉樹(shù)或非二叉樹(shù))。其每個(gè)非葉節(jié)點(diǎn)表示一個(gè)特征屬性上的測(cè)試,每個(gè)分支代表這個(gè)特征屬性在某個(gè)值域上的輸出,而每個(gè)葉節(jié)點(diǎn)存放一個(gè)類別。使用決策樹(shù)進(jìn)行決策的過(guò)程就是從根節(jié)點(diǎn)開(kāi)始,測(cè)試待分類項(xiàng)中相應(yīng)的特征屬性,并按照其值選擇輸出分支,直到到達(dá)葉子節(jié)點(diǎn),將葉子節(jié)點(diǎn)存放的類別作為決策結(jié)果。
信息增益
計(jì)算熵
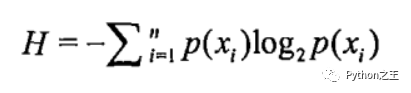
例子:
在決策樹(shù)當(dāng)中,設(shè)D為用類別對(duì)訓(xùn)練元組進(jìn)行的劃分,則D的熵(entropy)表示為: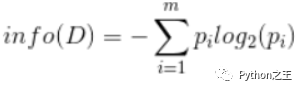
現(xiàn)在我們假設(shè)將訓(xùn)練元組D按屬性A進(jìn)行劃分,則A對(duì)D劃分的期望信息為 :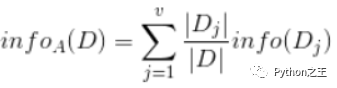
而信息增益即為兩者的差值: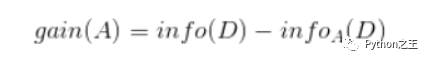
優(yōu)缺點(diǎn)
優(yōu)點(diǎn):計(jì)算復(fù)雜度不高,輸出結(jié)果易于理解,對(duì)中間值的缺失不敏感,可以處理不相關(guān)特征數(shù)據(jù)。既能用于分類,也能用于回歸
缺點(diǎn):可能會(huì)產(chǎn)生過(guò)度匹配問(wèn)題
導(dǎo)包
from?sklearn.tree?import?DecisionTreeClassifier
參數(shù)
max_depth: 樹(shù)的最大深度
梯度提升決策樹(shù)
導(dǎo)包和使用
from?sklearn.ensemble?import?GradientBoostingClassifier
GradientBoostingClassifier()
五、樸素貝葉斯
總結(jié)歷史,預(yù)測(cè)未來(lái)
【關(guān)鍵詞】
樸素:獨(dú)立性假設(shè)- 貝葉斯公式
思想
樸素貝葉斯中的樸素一詞的來(lái)源就是假設(shè)各特征之間相互獨(dú)立。這一假設(shè)使得樸素貝葉斯算法變得簡(jiǎn)單,但有時(shí)會(huì)犧牲一定的分類準(zhǔn)確率。?
公式
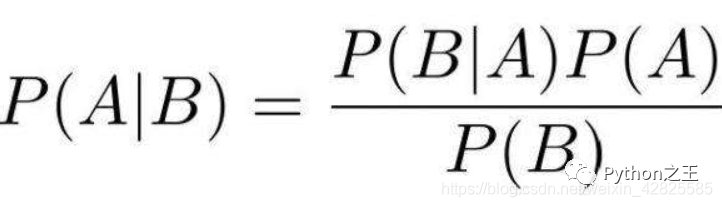
優(yōu)點(diǎn)
樸素貝葉斯模型發(fā)源于古典數(shù)學(xué)理論,有著堅(jiān)實(shí)的數(shù)學(xué)基礎(chǔ),以及穩(wěn)定的分類效率;- 對(duì)小規(guī)模的數(shù)據(jù)表現(xiàn)很好;- 能處理多分類任務(wù),適合增量式訓(xùn)練;- 對(duì)缺失數(shù)據(jù)不太敏感,算法也比較簡(jiǎn)單,常用于文本分類
缺點(diǎn)
只能用于分類問(wèn)題- 需要計(jì)算先驗(yàn)概率;- 分類決策存在錯(cuò)誤率;- 對(duì)輸入數(shù)據(jù)的表達(dá)形式很敏感
3種貝葉斯模型
高斯分布
高斯分布就是正態(tài)分布
【用途】用于一般分類問(wèn)題
導(dǎo)包
from?sklearn.naive_bayes?import?GaussianNB
多項(xiàng)式分布
公式
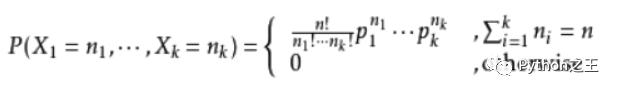
【用途】適用于文本數(shù)據(jù)(特征表示的是次數(shù),例如某個(gè)詞語(yǔ)的出現(xiàn)次數(shù))
導(dǎo)包
from?sklearn.naive_bayes?import?MultinomialNB
伯努利分布
【用途】適用于伯努利分布,也適用于文本數(shù)據(jù)(此時(shí)特征表示的是是否出現(xiàn),例如某個(gè)詞語(yǔ)的出現(xiàn)為1,不出現(xiàn)為0)
絕大多數(shù)情況下表現(xiàn)不如多項(xiàng)式分布,但有的時(shí)候伯努利分布表現(xiàn)得要比多項(xiàng)式分布要好,尤其是對(duì)于小數(shù)量級(jí)的文本數(shù)據(jù)
公式
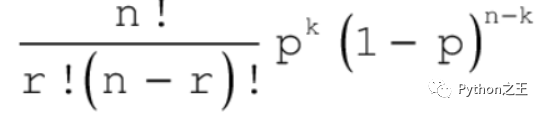
導(dǎo)包
from?sklearn.naive_bayes?import?BernoulliNB
六、隨機(jī)森林
極端的隨機(jī)森林
from?sklearn.ensemble?import?ExtraTreesRegressor
正常的隨機(jī)森林
from?sklearn.ensemble?import?RandomForestClassifier
特點(diǎn)
在當(dāng)前所有算法中,具有極好的準(zhǔn)確率- 能夠有效地運(yùn)行在大數(shù)據(jù)集上- 能夠處理具有高維特征的輸入樣本,而且不需要降維- 能夠評(píng)估各個(gè)特征在分類問(wèn)題上的重要性- 在生成過(guò)程中,能夠獲取到內(nèi)部生成誤差的一種無(wú)偏估計(jì)- 對(duì)于缺省值問(wèn)題也能夠獲得很好得結(jié)果
優(yōu)點(diǎn)
1、 在當(dāng)前的很多數(shù)據(jù)集上,相對(duì)其他算法有著很大的優(yōu)勢(shì),表現(xiàn)良好 2、它能夠處理很高維度的數(shù)據(jù),并且不用做特征選擇,因?yàn)樘卣髯蛹请S機(jī)選擇的 3、在訓(xùn)練完后,它能夠得出特征重要性 4、在創(chuàng)建隨機(jī)森林的時(shí)候,對(duì)generlization error使用的是無(wú)偏估計(jì),模型泛化能力強(qiáng) 5、隨機(jī)森林有oob,不需要單獨(dú)換分交叉驗(yàn)證集 6、訓(xùn)練時(shí)樹(shù)與樹(shù)之間是相互獨(dú)立的,訓(xùn)練速度快,容易做成并行化方法 7、對(duì)缺失值不敏感,如果有很大一部分的特征遺失,仍可以維持準(zhǔn)確度。
缺點(diǎn):
1、隨機(jī)森林在某些噪音較大的分類或回歸問(wèn)題上會(huì)過(guò)擬合 2、對(duì)于有不同取值的屬性的數(shù)據(jù),取值劃分較多的屬性會(huì)對(duì)隨機(jī)森林產(chǎn)生更大的影響
參數(shù)
n_estimators : 森林里(決策)樹(shù)的數(shù)目 **criterion : 衡量分裂質(zhì)量的性能(函數(shù))max_depth : 決策)樹(shù)的最大深度 **min_samples_split : 分割內(nèi)部節(jié)點(diǎn)所需要的最小樣本數(shù)量 **min_samples_leaf : 需要在葉子結(jié)點(diǎn)上的最小樣本數(shù)量 **min_weight_fraction_leaf : 一個(gè)葉子節(jié)點(diǎn)所需要的權(quán)重總和(所有的輸入樣本)的最小加權(quán)分?jǐn)?shù)n_jobs : 用于擬合和預(yù)測(cè)的并行運(yùn)行的工作作業(yè)數(shù)量 (進(jìn)程)
七、支持向量機(jī)SVM(Support Vector Machine)
原理
支持向量機(jī),其含義是通過(guò)支持向量運(yùn)算的分類器。其中“機(jī)”的意思是機(jī)器,可以理解為分類器。那么什么是支持向量呢?在求解的過(guò)程中,會(huì)發(fā)現(xiàn)只根據(jù)部分?jǐn)?shù)據(jù)就可以確定分類器,這些數(shù)據(jù)稱為支持向量
用途
SVM主要針對(duì)小樣本數(shù)據(jù)進(jìn)行學(xué)習(xí)、分類和預(yù)測(cè)(有時(shí)也叫回歸)的一種方法,能解決神經(jīng)網(wǎng)絡(luò)不能解決的過(guò)學(xué)習(xí)問(wèn)題,而且有很好的泛化能力
解決的問(wèn)題
線性分類 ?在訓(xùn)練數(shù)據(jù)中,每個(gè)數(shù)據(jù)都有n個(gè)的屬性和一個(gè)二類類別標(biāo)志,我們可以認(rèn)為這些數(shù)據(jù)在一個(gè)n維空間里。我們的目標(biāo)是找到一個(gè)n-1維的超平面(hyperplane),這個(gè)超平面可以將數(shù)據(jù)分成兩部分,每部分?jǐn)?shù)據(jù)都屬于同一個(gè)類別。其實(shí)這樣的超平面有很多,我們要找到一個(gè)最佳的。因此,增加一個(gè)約束條件:這個(gè)超平面到每邊最近數(shù)據(jù)點(diǎn)的距離是最大的。也成為最大間隔超平面(maximum-margin hyperplane)。這個(gè)分類器也成為最大間隔分類器(maximum-margin classifier)。支持向量機(jī)是一個(gè)二類分類器。- ?非線性分類 ?SVM的一個(gè)優(yōu)勢(shì)是支持非線性分類。它結(jié)合使用拉格朗日乘子法和KKT條件,以及核函數(shù)可以產(chǎn)生非線性分類器。
詳情
SVM的目的是要找到一個(gè)線性分類的最佳超平面 f(x)=xw+b=0。求 w 和 b。
首先通過(guò)兩個(gè)分類的最近點(diǎn),找到f(x)的約束條件。
有了約束條件,就可以通過(guò)拉格朗日乘子法和KKT條件來(lái)求解,這時(shí),問(wèn)題變成了求拉 格朗日乘子αi 和 b。
對(duì)于異常點(diǎn)的情況,加入松弛變量ξ來(lái)處理。
非線性分類的問(wèn)題:映射到高維度、使用核函數(shù)。
導(dǎo)包
from?sklearn.svm?import?SVC,SVR
參數(shù)
kernel:?linear??#?線性
?????rbf?????#?半徑
????????poly????#?多項(xiàng)式
八、K均值算法(K-means)聚類
【關(guān)鍵詞】K個(gè)種子,均值
原理
聚類的概念:一種無(wú)監(jiān)督的學(xué)習(xí),事先不知道類別,自動(dòng)將相似的對(duì)象歸到同一個(gè)簇中
K-Means算法是一種聚類分析(cluster analysis)的算法,其主要是來(lái)計(jì)算數(shù)據(jù)聚集的算法,主要通過(guò)不斷地取離種子點(diǎn)最近均值的算法。
K-Means算法的思想很簡(jiǎn)單,對(duì)于給定的樣本集,按照樣本之間的距離大小,將樣本集劃分為K個(gè)簇。讓簇內(nèi)的點(diǎn)盡量緊密的連在一起,而讓簇間的距離盡量的大
K-Means主要最重大的缺陷——都和初始值有關(guān)
K是事先給定的,這個(gè)K值的選定是非常難以估計(jì)的。很多時(shí)候,事先并不知道給定的數(shù)據(jù)集應(yīng)該分成多少個(gè)類別才最合適。(ISODATA算法通過(guò)類的自動(dòng)合并和分裂,得到較為合理的類型數(shù)目K)
K-Means算法需要用初始隨機(jī)種子點(diǎn)來(lái)搞,這個(gè)隨機(jī)種子點(diǎn)太重要,不同的隨機(jī)種子點(diǎn)會(huì)有得到完全不同的結(jié)果。(K-Means++算法可以用來(lái)解決這個(gè)問(wèn)題,其可以有效地選擇初始點(diǎn))
步驟
從數(shù)據(jù)中選擇k個(gè)對(duì)象作為初始聚類中心;1. 計(jì)算每個(gè)聚類對(duì)象到聚類中心的距離來(lái)劃分;1. 再次計(jì)算每個(gè)聚類中心1. 計(jì)算標(biāo)準(zhǔn)測(cè)度函數(shù),直到達(dá)到最大迭代次數(shù),則停止,否則,繼續(xù)操作。1. 確定最優(yōu)的聚類中心
參數(shù)和屬性
重要參數(shù):
n_clusters:聚類的個(gè)數(shù) 重要屬性: cluster_centers_ : [n_clusters, n_features]的數(shù)組,表示聚類中心點(diǎn)的坐標(biāo)- labels_ : 每個(gè)樣本點(diǎn)的標(biāo)簽
導(dǎo)包
from?sklearn.cluster?import?KMeans
常見(jiàn)錯(cuò)誤
k值不合適1. 數(shù)據(jù)偏差1. 標(biāo)準(zhǔn)偏差不相同1. 樣本數(shù)量不同
聚類評(píng)估:輪廓系數(shù)
導(dǎo)包
from?sklearn.metrics?import?silhouette_score
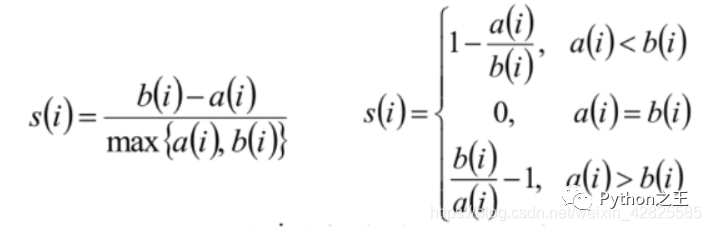
計(jì)算樣本i到同簇其他樣本的平均距離ai。ai 越小,說(shuō)明樣本i越應(yīng)該被聚類到該簇。將ai 稱為樣本i的簇內(nèi)不相似度。- ?計(jì)算樣本i到其他某簇Cj 的所有樣本的平均距離bij,稱為樣本i與簇Cj 的不相似度。定義為樣本i的簇間不相似度:bi =min{bi1, bi2, …, bik} - ?si接近1,則說(shuō)明樣本i聚類合理 - ?si接近-1,則說(shuō)明樣本i更應(yīng)該分類到另外的簇 - ?若si 近似為0,則說(shuō)明樣本i在兩個(gè)簇的邊界上。
使用
#?需要傳訓(xùn)練數(shù)據(jù)和預(yù)測(cè)的結(jié)果
silhouette_samples(data,?labels)?#?返回的是每一個(gè)樣本的輪廓系數(shù).
九、交叉驗(yàn)證(尋找最優(yōu)算法)
用于系統(tǒng)地遍歷多種參數(shù)組合,通過(guò)交叉驗(yàn)證確定最佳效果參數(shù)
導(dǎo)包與使用
from?sklearn.model_selection?import?GridSearchCV
knn?=?KNeighborsClassifier()
param_grid?=?{
????'n_neighbors':?[3,5,7,9,11],?
????'weights':?['uniform',?'distance'],
????'p':?[1,2]
}
gv?=?GridSearchCV(knn,?param_grid=param_grid,?n_jobs=5)#?param_grid為參數(shù)字典?n_jobs?為進(jìn)程數(shù)
屬性
gv.best_score_ : 最佳得分- gv.best_estimator_ : 最佳的算法對(duì)象- gv.best_params_ : 最佳參數(shù)
十、PCA降維
導(dǎo)包與使用
from?sklearn.decomposition?import?PCA
#?n_components表示要降到多少維,?
#?whiten?=?True?,白化,?把數(shù)據(jù)的標(biāo)準(zhǔn)差變的一致.
pca?=?PCA(30,?whiten=True)
pca.fit_transform(data)?#?data為高維數(shù)組
十一: 特征工程
描述
特征是指數(shù)據(jù)中抽取出來(lái)的對(duì)結(jié)果預(yù)測(cè)有用的信息- 特征工程是使用專業(yè)背景和技巧處理數(shù)據(jù),使得特征能在機(jī)器學(xué)習(xí)算法上發(fā)揮更好的作用的過(guò)程
意義
更好的特征意味著更強(qiáng)的靈活性- 更好的特征意味著只需要簡(jiǎn)單模型- 更好的特征意味著更好的結(jié)果
數(shù)據(jù)清洗方式
錯(cuò)誤數(shù)據(jù)- 組合或統(tǒng)計(jì)屬性判定- 補(bǔ)齊可對(duì)應(yīng)的缺省值
正負(fù)樣本不平衡的處理方法
正負(fù)樣本量很大,一類樣本數(shù)量 >> 另一類樣本數(shù)量, 采用下采樣,即對(duì)偏多的數(shù)據(jù)進(jìn)行采樣,使兩類樣本數(shù)量達(dá)到一定比例,例如1:1, 3:2等 正負(fù)樣本量不大, 一類樣本數(shù)量>>另一類樣本
采集更多的數(shù)據(jù)- oversampling,即硬生生的增加量少的一方的樣本,比如增加幾倍的量少的樣本(或簡(jiǎn)單處理量少的數(shù)據(jù),例如圖像識(shí)別中的鏡像、旋轉(zhuǎn)),容易過(guò)擬合- 修改loss function,例如增加量大的樣本的懲罰權(quán)重
十二、分類模型
描述
AUC是一個(gè)模型評(píng)價(jià)指標(biāo),用于二分類模型的評(píng)價(jià)。AUC是“Area under Curve(曲線下的面積)”的英文縮寫(xiě),而這條“Curve(曲線)”就是ROC曲線。
AUC是現(xiàn)在分類模型,特別是二分類模型使用的主要離線評(píng)測(cè)指標(biāo)之一 .
相比于準(zhǔn)確率、召回率、F1等指標(biāo),AUC有一個(gè)獨(dú)特的優(yōu)勢(shì),就是不關(guān)注具體得分,只關(guān)注排序結(jié)果,這使得它特別適用于排序問(wèn)題的效果評(píng)估,例如推薦排序的評(píng)估。AUC這個(gè)指標(biāo)有兩種解釋方法,一種是傳統(tǒng)的“曲線下面積”解釋,另一種是關(guān)于排序能力的解釋。例如0.7的AUC,其含義可以大概理解為:給定一個(gè)正樣本和一個(gè)負(fù)樣本,在70%的情況下,模型對(duì)正樣本的打分高于對(duì)負(fù)樣本的打分。可以看出在這個(gè)解釋下,我們關(guān)心的只有正負(fù)樣本之間的分?jǐn)?shù)高低,而具體的分值則無(wú)關(guān)緊要。
為什么要使用
為什么要用AUC作為二分類模型的評(píng)價(jià)指標(biāo)呢?為什么不直接通過(guò)計(jì)算準(zhǔn)確率來(lái)對(duì)模型進(jìn)行評(píng)價(jià)呢?答案是這樣的:機(jī)器學(xué)習(xí)中的很多模型對(duì)于分類問(wèn)題的預(yù)測(cè)結(jié)果大多是概率,即屬于某個(gè)類別的概率,如果計(jì)算準(zhǔn)確率的話,就要把概率轉(zhuǎn)化為類別,這就需要設(shè)定一個(gè)閾值,概率大于某個(gè)閾值的屬于一類,概率小于某個(gè)閾值的屬于另一類,而閾值的設(shè)定直接影響了準(zhǔn)確率的計(jì)算。使用AUC可以解決這個(gè)問(wèn)題,接下來(lái)詳細(xì)介紹AUC的計(jì)算。
導(dǎo)包
from?sklearn.metrics?import?roc_curve,?auc
一個(gè)分類模型的分類結(jié)果的好壞取決于以下兩個(gè)部分:
分類模型的排序能力(能否把概率高的排前面,概率低的排后面)1. threshold的選擇
ROC
圖
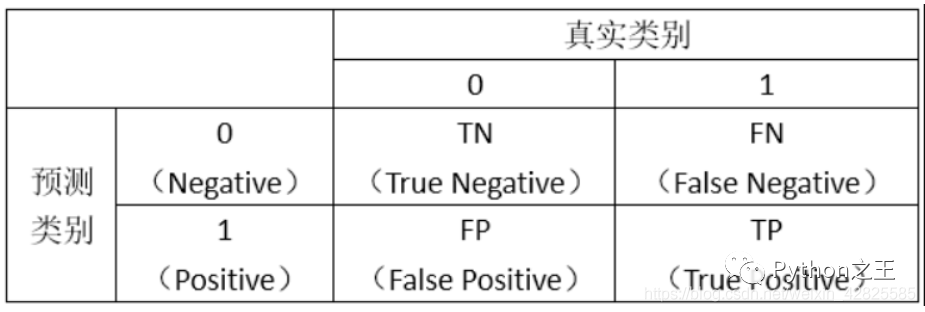
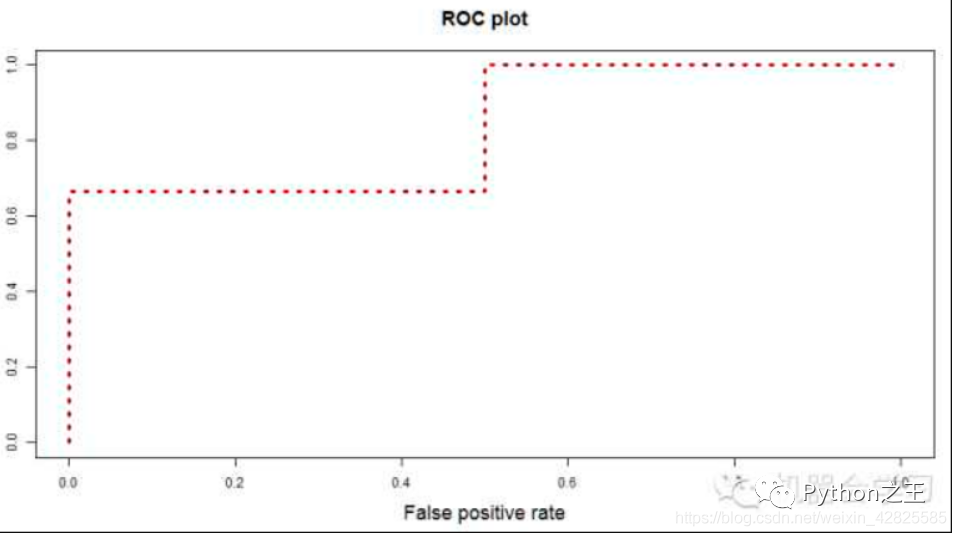
計(jì)算兩個(gè)指標(biāo)的值:??True Positive Rate=TP/(TP+FN),代表將真實(shí)正樣本劃分為正樣本的概率 真陽(yáng)率 ??False Positive Rate=FP/(FP+TN),代表將真實(shí)負(fù)樣本劃分為正樣本的概率 偽陽(yáng)率 ??接著,我們以“True Positive Rate”作為縱軸,以“False Positive Rate”作為橫軸,畫(huà)出ROC曲線。類似下圖:
代碼演示:
logistic?=?LogisticRegression()
i?=?1
#?人為的創(chuàng)造fpr_mean
fpr_mean?=?np.linspace(0,1,?100)
tprs?=?[]
aucs?=?[]
for?train,test?in?skf.split(X,y):
????
????logistic.fit(X[train],?y[train])
????y_?=?logistic.predict_proba(X[test])
#?????print(y_)
#?????print('----------------------------------')
????#?真實(shí)值,和正例的概率
????fpr,?tpr,?thresholds?=?roc_curve(y[test],?y_[:,1])
????tpr_mean?=?interp(fpr_mean?,fpr,?tpr)
????tprs.append(tpr_mean)
#?????print(fpr,?tpr,?thresholds)
#?????print('---------------------------------------')
????auc_?=?auc(fpr,?tpr)
????aucs.append(auc_)
????plt.plot(fpr,?tpr,?label=f'fold?{i},?auc:?%.4f'?%?(auc_),?alpha=.4)
????i?+=?1
????
tprs?=?np.array(tprs)
tpr_mean?=?tprs.mean(axis=0)
tpr_mean[0]?=?0
tpr_mean[-1]?=?1
auc_mean?=?auc(fpr_mean,?tpr_mean)
#?算auc的標(biāo)準(zhǔn)差
aucs?=?np.array(aucs)
auc_std?=?aucs.std(axis=0)
plt.plot(fpr_mean,?tpr_mean,?label='auc?mean:?%.4f$\pm$%.4f'?%?(auc_mean,?auc_std),c='g')
plt.legend()


既往專輯
 | |