數(shù)據(jù)特征選擇
特征選擇(排序)對(duì)于數(shù)據(jù)科學(xué)家、機(jī)器學(xué)習(xí)從業(yè)者來說非常重要。好的特征選擇能夠提升模型的性能,更能幫助我們理解數(shù)據(jù)的特點(diǎn)、底層結(jié)構(gòu),這對(duì)進(jìn)一步改善模型、算法都有著重要作用。
特征選擇主要有兩個(gè)功能:
減少特征數(shù)量、降維,使模型泛化能力更強(qiáng),減少過擬合
增強(qiáng)對(duì)特征和特征值之間的理解
拿到數(shù)據(jù)集,一個(gè)特征選擇方法,往往很難同時(shí)完成這兩個(gè)目的。通常情況下,我們經(jīng)常不管三七二十一,選擇一種自己最熟悉或者最方便的特征選擇方法(往往目的是降維,而忽略了對(duì)特征和數(shù)據(jù)理解的目的)。
在許多機(jī)器學(xué)習(xí)相關(guān)的書里,很難找到關(guān)于特征選擇的內(nèi)容,因?yàn)樘卣鬟x擇要解決的問題往往被視為機(jī)器學(xué)習(xí)的一種副作用,一般不會(huì)單獨(dú)拿出來討論。
本文將結(jié)合?Scikit-learn提供的例子?介紹幾種常用的特征選擇方法,它們各自的優(yōu)缺點(diǎn)和問題。
?1 去掉取值變化小的特征 Removing features with low variance
這應(yīng)該是最簡(jiǎn)單的特征選擇方法了:假設(shè)某特征的特征值只有0和1,并且在所有輸入樣本中,95%的實(shí)例的該特征取值都是1,那就可以認(rèn)為這個(gè)特征作用不大。如果100%都是1,那這個(gè)特征就沒意義了。當(dāng)特征值都是離散型變量的時(shí)候這種方法才能用,如果是連續(xù)型變量,就需要將連續(xù)變量離散化之后才能用,而且實(shí)際當(dāng)中,一般不太會(huì)有95%以上都取某個(gè)值的特征存在,所以這種方法雖然簡(jiǎn)單但是不太好用。可以把它作為特征選擇的預(yù)處理,先去掉那些取值變化小的特征,然后再?gòu)慕酉聛硖岬降牡奶卣鬟x擇方法中選擇合適的進(jìn)行進(jìn)一步的特征選擇。
?2 單變量特征選擇 Univariate feature selection
單變量特征選擇能夠?qū)γ恳粋€(gè)特征進(jìn)行測(cè)試,衡量該特征和響應(yīng)變量之間的關(guān)系,根據(jù)得分扔掉不好的特征。對(duì)于回歸和分類問題可以采用卡方檢驗(yàn)等方式對(duì)特征進(jìn)行測(cè)試。
這種方法比較簡(jiǎn)單,易于運(yùn)行,易于理解,通常對(duì)于理解數(shù)據(jù)有較好的效果(但對(duì)特征優(yōu)化、提高泛化能力來說不一定有效);這種方法有許多改進(jìn)的版本、變種。
?2.1 Pearson相關(guān)系數(shù) Pearson Correlation
皮爾森相關(guān)系數(shù)是一種最簡(jiǎn)單的,能幫助理解特征和響應(yīng)變量之間關(guān)系的方法,該方法衡量的是變量之間的線性相關(guān)性,結(jié)果的取值區(qū)間為[-1,1],-1表示完全的負(fù)相關(guān)(這個(gè)變量下降,那個(gè)就會(huì)上升),+1表示完全的正相關(guān),0表示沒有線性相關(guān)。
Pearson Correlation速度快、易于計(jì)算,經(jīng)常在拿到數(shù)據(jù)(經(jīng)過清洗和特征提取之后的)之后第一時(shí)間就執(zhí)行。Scipy的?pearsonr?方法能夠同時(shí)計(jì)算相關(guān)系數(shù)和p-value,
import numpy as np
from scipy.stats import pearsonr
np.random.seed(0)
size = 300
x = np.random.normal(0, 1, size)
print "Lower noise", pearsonr(x, x + np.random.normal(0, 1, size))
print "Higher noise", pearsonr(x, x + np.random.normal(0, 10, size))Lower noise (0.71824836862138386, 7.3240173129992273e-49)Higher noise (0.057964292079338148, 0.31700993885324746)
這個(gè)例子中,我們比較了變量在加入噪音之前和之后的差異。當(dāng)噪音比較小的時(shí)候,相關(guān)性很強(qiáng),p-value很低。
Scikit-learn提供的?f_regrssion?方法能夠批量計(jì)算特征的p-value,非常方便,參考sklearn的?pipeline
Pearson相關(guān)系數(shù)的一個(gè)明顯缺陷是,作為特征排序機(jī)制,他只對(duì)線性關(guān)系敏感。如果關(guān)系是非線性的,即便兩個(gè)變量具有一一對(duì)應(yīng)的關(guān)系,Pearson相關(guān)性也可能會(huì)接近0。
x = np.random.uniform(-1, 1, 100000)
print pearsonr(x, x**2)[0]
-0.00230804707612
更多類似的例子參考?sample plots?。另外,如果僅僅根據(jù)相關(guān)系數(shù)這個(gè)值來判斷的話,有時(shí)候會(huì)具有很強(qiáng)的誤導(dǎo)性,如?Anscombe’s quartet?,最好把數(shù)據(jù)可視化出來,以免得出錯(cuò)誤的結(jié)論。
2.2 互信息和最大信息系數(shù) Mutual information and maximal information coefficient (MIC)
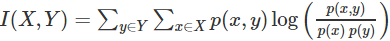
以上就是經(jīng)典的互信息公式了。想把互信息直接用于特征選擇其實(shí)不是太方便:1、它不屬于度量方式,也沒有辦法歸一化,在不同數(shù)據(jù)及上的結(jié)果無法做比較;2、對(duì)于連續(xù)變量的計(jì)算不是很方便(X和Y都是集合,x,y都是離散的取值),通常變量需要先離散化,而互信息的結(jié)果對(duì)離散化的方式很敏感。
最大信息系數(shù)克服了這兩個(gè)問題。它首先尋找一種最優(yōu)的離散化方式,然后把互信息取值轉(zhuǎn)換成一種度量方式,取值區(qū)間在[0,1]。?minepy?提供了MIC功能。
反過頭來看y=x^2這個(gè)例子,MIC算出來的互信息值為1(最大的取值)。
from minepy import MINE
m = MINE()
x = np.random.uniform(-1, 1, 10000)
m.compute_score(x, x**2)
print m.mic()1.0
MIC的統(tǒng)計(jì)能力遭到了?一些質(zhì)疑?,當(dāng)零假設(shè)不成立時(shí),MIC的統(tǒng)計(jì)就會(huì)受到影響。在有的數(shù)據(jù)集上不存在這個(gè)問題,但有的數(shù)據(jù)集上就存在這個(gè)問題。
?2.3 距離相關(guān)系數(shù) (Distance correlation)
距離相關(guān)系數(shù)是為了克服Pearson相關(guān)系數(shù)的弱點(diǎn)而生的。在x和x^2這個(gè)例子中,即便Pearson相關(guān)系數(shù)是0,我們也不能斷定這兩個(gè)變量是獨(dú)立的(有可能是非線性相關(guān));但如果距離相關(guān)系數(shù)是0,那么我們就可以說這兩個(gè)變量是獨(dú)立的。
R的?energy?包里提供了距離相關(guān)系數(shù)的實(shí)現(xiàn),另外這是?Python gist?的實(shí)現(xiàn)。
#R-code
> x = runif (1000, -1, 1)
> dcor(x, x**2)
[1] 0.4943864
盡管有MIC和距離相關(guān)系數(shù)在了,但當(dāng)變量之間的關(guān)系接近線性相關(guān)的時(shí)候,Pearson相關(guān)系數(shù)仍然是不可替代的。第一、Pearson相關(guān)系數(shù)計(jì)算速度快,這在處理大規(guī)模數(shù)據(jù)的時(shí)候很重要。第二、Pearson相關(guān)系數(shù)的取值區(qū)間是[-1,1],而MIC和距離相關(guān)系數(shù)都是[0,1]。這個(gè)特點(diǎn)使得Pearson相關(guān)系數(shù)能夠表征更豐富的關(guān)系,符號(hào)表示關(guān)系的正負(fù),絕對(duì)值能夠表示強(qiáng)度。當(dāng)然,Pearson相關(guān)性有效的前提是兩個(gè)變量的變化關(guān)系是單調(diào)的。
?2.4 基于學(xué)習(xí)模型的特征排序 (Model based ranking)
這種方法的思路是直接使用你要用的機(jī)器學(xué)習(xí)算法,針對(duì)每個(gè)單獨(dú)的特征和響應(yīng)變量建立預(yù)測(cè)模型。其實(shí)Pearson相關(guān)系數(shù)等價(jià)于線性回歸里的標(biāo)準(zhǔn)化回歸系數(shù)。假如某個(gè)特征和響應(yīng)變量之間的關(guān)系是非線性的,可以用基于樹的方法(決策樹、隨機(jī)森林)、或者擴(kuò)展的線性模型等。基于樹的方法比較易于使用,因?yàn)樗麄儗?duì)非線性關(guān)系的建模比較好,并且不需要太多的調(diào)試。但要注意過擬合問題,因此樹的深度最好不要太大,再就是運(yùn)用交叉驗(yàn)證。
在?波士頓房?jī)r(jià)數(shù)據(jù)集?上使用sklearn的?隨機(jī)森林回歸?給出一個(gè)單變量選擇的例子:
from sklearn.cross_validation import cross_val_score, ShuffleSplit
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
#Load boston housing dataset as an example
boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]
rf = RandomForestRegressor(n_estimators=20, max_depth=4)
scores = []
for i in range(X.shape[1]):
score = cross_val_score(rf, X[:, i:i+1], Y, scoring="r2",
cv=ShuffleSplit(len(X), 3, .3))
scores.append((round(np.mean(score), 3), names[i]))
print sorted(scores, reverse=True)[(0.636, ‘LSTAT’), (0.59, ‘RM’), (0.472, ‘NOX’), (0.369, ‘INDUS’), (0.311, ‘PTRATIO’), (0.24, ‘TAX’), (0.24, ‘CRIM’), (0.185, ‘RAD’), (0.16, ‘ZN’), (0.087, ‘B’), (0.062, ‘DIS’), (0.036, ‘CHAS’), (0.027, ‘AGE’)]
3 線性模型和正則化
單變量特征選擇方法獨(dú)立的衡量每個(gè)特征與響應(yīng)變量之間的關(guān)系,另一種主流的特征選擇方法是基于機(jī)器學(xué)習(xí)模型的方法。有些機(jī)器學(xué)習(xí)方法本身就具有對(duì)特征進(jìn)行打分的機(jī)制,或者很容易將其運(yùn)用到特征選擇任務(wù)中,例如回歸模型,SVM,決策樹,隨機(jī)森林等等。說句題外話,這種方法好像在一些地方叫做wrapper類型,大概意思是說,特征排序模型和機(jī)器學(xué)習(xí)模型是耦盒在一起的,對(duì)應(yīng)的非wrapper類型的特征選擇方法叫做filter類型。
下面將介紹如何用回歸模型的系數(shù)來選擇特征。越是重要的特征在模型中對(duì)應(yīng)的系數(shù)就會(huì)越大,而跟輸出變量越是無關(guān)的特征對(duì)應(yīng)的系數(shù)就會(huì)越接近于0。在噪音不多的數(shù)據(jù)上,或者是數(shù)據(jù)量遠(yuǎn)遠(yuǎn)大于特征數(shù)的數(shù)據(jù)上,如果特征之間相對(duì)來說是比較獨(dú)立的,那么即便是運(yùn)用最簡(jiǎn)單的線性回歸模型也一樣能取得非常好的效果。
from sklearn.linear_model import LinearRegression
import numpy as np
np.random.seed(0)
size = 5000
#A dataset with 3 features
X = np.random.normal(0, 1, (size, 3))
#Y = X0 + 2*X1 + noise
Y = X[:,0] + 2*X[:,1] + np.random.normal(0, 2, size)
lr = LinearRegression()
lr.fit(X, Y)
#A helper method for pretty-printing linear models
def pretty_print_linear(coefs, names = None, sort = False):
if names == None:
names = ["X%s" % x for x in range(len(coefs))]
lst = zip(coefs, names)
if sort:
lst = sorted(lst, key = lambda x:-np.abs(x[0]))
return " + ".join("%s * %s" % (round(coef, 3), name)
for coef, name in lst)
print "Linear model:", pretty_print_linear(lr.coef_)
Linear model: 0.984 * X0 + 1.995 * X1 + -0.041 * X2
在這個(gè)例子當(dāng)中,盡管數(shù)據(jù)中存在一些噪音,但這種特征選擇模型仍然能夠很好的體現(xiàn)出數(shù)據(jù)的底層結(jié)構(gòu)。當(dāng)然這也是因?yàn)槔又械倪@個(gè)問題非常適合用線性模型來解:特征和響應(yīng)變量之間全都是線性關(guān)系,并且特征之間均是獨(dú)立的。
在很多實(shí)際的數(shù)據(jù)當(dāng)中,往往存在多個(gè)互相關(guān)聯(lián)的特征,這時(shí)候模型就會(huì)變得不穩(wěn)定,數(shù)據(jù)中細(xì)微的變化就可能導(dǎo)致模型的巨大變化(模型的變化本質(zhì)上是系數(shù),或者叫參數(shù),可以理解成W),這會(huì)讓模型的預(yù)測(cè)變得困難,這種現(xiàn)象也稱為多重共線性。例如,假設(shè)我們有個(gè)數(shù)據(jù)集,它的真實(shí)模型應(yīng)該是Y=X1+X2,當(dāng)我們觀察的時(shí)候,發(fā)現(xiàn)Y’=X1+X2+e,e是噪音。如果X1和X2之間存在線性關(guān)系,例如X1約等于X2,這個(gè)時(shí)候由于噪音e的存在,我們學(xué)到的模型可能就不是Y=X1+X2了,有可能是Y=2X1,或者Y=-X1+3X2。
下邊這個(gè)例子當(dāng)中,在同一個(gè)數(shù)據(jù)上加入了一些噪音,用隨機(jī)森林算法進(jìn)行特征選擇。
from sklearn.linear_model import LinearRegression
size = 100
np.random.seed(seed=5)
X_seed = np.random.normal(0, 1, size)
X1 = X_seed + np.random.normal(0, .1, size)
X2 = X_seed + np.random.normal(0, .1, size)
X3 = X_seed + np.random.normal(0, .1, size)
Y = X1 + X2 + X3 + np.random.normal(0,1, size)
X = np.array([X1, X2, X3]).T
lr = LinearRegression()
lr.fit(X,Y)
print "Linear model:", pretty_print_linear(lr.coef_)?Linear model: -1.291 * X0 + 1.591 * X1 + 2.747 * X2
系數(shù)之和接近3,基本上和上上個(gè)例子的結(jié)果一致,應(yīng)該說學(xué)到的模型對(duì)于預(yù)測(cè)來說還是不錯(cuò)的。但是,如果從系數(shù)的字面意思上去解釋特征的重要性的話,X3對(duì)于輸出變量來說具有很強(qiáng)的正面影響,而X1具有負(fù)面影響,而實(shí)際上所有特征與輸出變量之間的影響是均等的。
? 同樣的方法和套路可以用到類似的線性模型上,比如邏輯回歸。
3.1 正則化模型
正則化就是把額外的約束或者懲罰項(xiàng)加到已有模型(損失函數(shù))上,以防止過擬合并提高泛化能力。損失函數(shù)由原來的E(X,Y)變?yōu)镋(X,Y)+alpha||w||,w是模型系數(shù)組成的向量(有些地方也叫參數(shù)parameter,coefficients),||·||一般是L1或者L2范數(shù),alpha是一個(gè)可調(diào)的參數(shù),控制著正則化的強(qiáng)度。當(dāng)用在線性模型上時(shí),L1正則化和L2正則化也稱為L(zhǎng)asso和Ridge。
?3.2 L1正則化/Lasso
L1正則化將系數(shù)w的l1范數(shù)作為懲罰項(xiàng)加到損失函數(shù)上,由于正則項(xiàng)非零,這就迫使那些弱的特征所對(duì)應(yīng)的系數(shù)變成0。因此L1正則化往往會(huì)使學(xué)到的模型很稀疏(系數(shù)w經(jīng)常為0),這個(gè)特性使得L1正則化成為一種很好的特征選擇方法。
Scikit-learn為線性回歸提供了Lasso,為分類提供了L1邏輯回歸。
下面的例子在波士頓房?jī)r(jià)數(shù)據(jù)上運(yùn)行了Lasso,其中參數(shù)alpha是通過grid search進(jìn)行優(yōu)化的。
from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston
boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
Y = boston["target"]
names = boston["feature_names"]
lasso = Lasso(alpha=.3)
lasso.fit(X, Y)
print "Lasso model: ", pretty_print_linear(lasso.coef_, names, sort = True)Lasso model: -3.707 * LSTAT + 2.992 * RM + -1.757 * PTRATIO + -1.081 * DIS + -0.7 * NOX + 0.631 * B + 0.54 * CHAS + -0.236 * CRIM + 0.081 * ZN + -0.0 * INDUS + -0.0 * AGE + 0.0 * RAD + -0.0 * TAX
可以看到,很多特征的系數(shù)都是0。如果繼續(xù)增加alpha的值,得到的模型就會(huì)越來越稀疏,即越來越多的特征系數(shù)會(huì)變成0。
然而,L1正則化像非正則化線性模型一樣也是不穩(wěn)定的,如果特征集合中具有相關(guān)聯(lián)的特征,當(dāng)數(shù)據(jù)發(fā)生細(xì)微變化時(shí)也有可能導(dǎo)致很大的模型差異。
?3.3 L2正則化/Ridge regression
L2正則化將系數(shù)向量的L2范數(shù)添加到了損失函數(shù)中。由于L2懲罰項(xiàng)中系數(shù)是二次方的,這使得L2和L1有著諸多差異,最明顯的一點(diǎn)就是,L2正則化會(huì)讓系數(shù)的取值變得平均。對(duì)于關(guān)聯(lián)特征,這意味著他們能夠獲得更相近的對(duì)應(yīng)系數(shù)。還是以Y=X1+X2為例,假設(shè)X1和X2具有很強(qiáng)的關(guān)聯(lián),如果用L1正則化,不論學(xué)到的模型是Y=X1+X2還是Y=2X1,懲罰都是一樣的,都是2?alpha。但是對(duì)于L2來說,第一個(gè)模型的懲罰項(xiàng)是2alpha,但第二個(gè)模型的是4*alpha。可以看出,系數(shù)之和為常數(shù)時(shí),各系數(shù)相等時(shí)懲罰是最小的,所以才有了L2會(huì)讓各個(gè)系數(shù)趨于相同的特點(diǎn)。
可以看出,L2正則化對(duì)于特征選擇來說一種穩(wěn)定的模型,不像L1正則化那樣,系數(shù)會(huì)因?yàn)榧?xì)微的數(shù)據(jù)變化而波動(dòng)。所以L2正則化和L1正則化提供的價(jià)值是不同的,L2正則化對(duì)于特征理解來說更加有用:表示能力強(qiáng)的特征對(duì)應(yīng)的系數(shù)是非零。
回過頭來看看3個(gè)互相關(guān)聯(lián)的特征的例子,分別以10個(gè)不同的種子隨機(jī)初始化運(yùn)行10次,來觀察L1和L2正則化的穩(wěn)定性。
from sklearn.linear_model import Ridge
from sklearn.metrics import r2_score
size = 100
#We run the method 10 times with different random seeds
for i in range(10):
print "Random seed %s" % i
np.random.seed(seed=i)
X_seed = np.random.normal(0, 1, size)
X1 = X_seed + np.random.normal(0, .1, size)
X2 = X_seed + np.random.normal(0, .1, size)
X3 = X_seed + np.random.normal(0, .1, size)
Y = X1 + X2 + X3 + np.random.normal(0, 1, size)
X = np.array([X1, X2, X3]).T
lr = LinearRegression()
lr.fit(X,Y)
print "Linear model:", pretty_print_linear(lr.coef_)
ridge = Ridge(alpha=10)
ridge.fit(X,Y)
print "Ridge model:", pretty_print_linear(ridge.coef_)
print
Random seed 0 Linear model: 0.728 * X0 + 2.309 * X1 + -0.082 * X2 Ridge model: 0.938 * X0 + 1.059 * X1 + 0.877 * X2
Random seed 1 Linear model: 1.152 * X0 + 2.366 * X1 + -0.599 * X2 Ridge model: 0.984 * X0 + 1.068 * X1 + 0.759 * X2
Random seed 2 Linear model: 0.697 * X0 + 0.322 * X1 + 2.086 * X2 Ridge model: 0.972 * X0 + 0.943 * X1 + 1.085 * X2
Random seed 3 Linear model: 0.287 * X0 + 1.254 * X1 + 1.491 * X2 Ridge model: 0.919 * X0 + 1.005 * X1 + 1.033 * X2
Random seed 4 Linear model: 0.187 * X0 + 0.772 * X1 + 2.189 * X2 Ridge model: 0.964 * X0 + 0.982 * X1 + 1.098 * X2
Random seed 5 Linear model: -1.291 * X0 + 1.591 * X1 + 2.747 * X2 Ridge model: 0.758 * X0 + 1.011 * X1 + 1.139 * X2
Random seed 6 Linear model: 1.199 * X0 + -0.031 * X1 + 1.915 * X2 Ridge model: 1.016 * X0 + 0.89 * X1 + 1.091 * X2
Random seed 7 Linear model: 1.474 * X0 + 1.762 * X1 + -0.151 * X2 Ridge model: 1.018 * X0 + 1.039 * X1 + 0.901 * X2
Random seed 8 Linear model: 0.084 * X0 + 1.88 * X1 + 1.107 * X2 Ridge model: 0.907 * X0 + 1.071 * X1 + 1.008 * X2
Random seed 9 Linear model: 0.714 * X0 + 0.776 * X1 + 1.364 * X2 Ridge model: 0.896 * X0 + 0.903 * X1 + 0.98 * X2
?? 可以看出,不同的數(shù)據(jù)上線性回歸得到的模型(系數(shù))相差甚遠(yuǎn),但對(duì)于L2正則化模型來說,結(jié)果中的系數(shù)非常的穩(wěn)定,差別較小,都比較接近于1,能夠反映出數(shù)據(jù)的內(nèi)在結(jié)構(gòu)。
