數(shù)據(jù)特征選擇（三）

?5 兩種頂層特征選擇算法

之所以叫做頂層，是因?yàn)樗麄兌际墙⒃诨谀Ｐ偷奶卣鬟x擇方法基礎(chǔ)之上的，例如回歸和SVM，在不同的子集上建立模型，然后匯總最終確定特征得分。

?5.1 穩(wěn)定性選擇 Stability selection

穩(wěn)定性選擇是一種基于二次抽樣和選擇算法相結(jié)合較新的方法，選擇算法可以是回歸、SVM或其他類(lèi)似的方法。它的主要思想是在不同的數(shù)據(jù)子集和特征子集上運(yùn)行特征選擇算法，不斷的重復(fù)，最終匯總特征選擇結(jié)果，比如可以統(tǒng)計(jì)某個(gè)特征被認(rèn)為是重要特征的頻率（被選為重要特征的次數(shù)除以它所在的子集被測(cè)試的次數(shù)）。理想情況下，重要特征的得分會(huì)接近100%。稍微弱一點(diǎn)的特征得分會(huì)是非0的數(shù)，而最無(wú)用的特征得分將會(huì)接近于0。

sklearn在?隨機(jī)lasso?和?隨機(jī)邏輯回歸?中有對(duì)穩(wěn)定性選擇的實(shí)現(xiàn)。

from sklearn.linear_model import RandomizedLasso
from sklearn.datasets import load_boston
boston = load_boston()

#using the Boston housing data.
#Data gets scaled automatically by sklearn's implementation
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]

rlasso = RandomizedLasso(alpha=0.025)
rlasso.fit(X, Y)

print "Features sorted by their score:"
print sorted(zip(map(lambda x: round(x, 4), rlasso.scores_), 
                 names), reverse=True)

Features sorted by their score: [(1.0, ‘RM’), (1.0, ‘PTRATIO’), (1.0, ‘LSTAT’), (0.62, ‘CHAS’), (0.595, ‘B’), (0.39, ‘TAX’), (0.385, ‘CRIM’), (0.25, ‘DIS’), (0.22, ‘NOX’), (0.125, ‘INDUS’), (0.045, ‘ZN’), (0.02, ‘RAD’), (0.015, ‘AGE’)]

在上邊這個(gè)例子當(dāng)中，最高的3個(gè)特征得分是1.0，這表示他們總會(huì)被選作有用的特征（當(dāng)然，得分會(huì)收到正則化參數(shù)alpha的影響，但是sklearn的隨機(jī)lasso能夠自動(dòng)選擇最優(yōu)的alpha）。接下來(lái)的幾個(gè)特征得分就開(kāi)始下降，但是下降的不是特別急劇，這跟純lasso的方法和隨機(jī)森林的結(jié)果不一樣。能夠看出穩(wěn)定性選擇對(duì)于克服過(guò)擬合和對(duì)數(shù)據(jù)理解來(lái)說(shuō)都是有幫助的：總的來(lái)說(shuō)，好的特征不會(huì)因?yàn)橛邢嗨频奶卣鳌㈥P(guān)聯(lián)特征而得分為0，這跟Lasso是不同的。對(duì)于特征選擇任務(wù)，在許多數(shù)據(jù)集和環(huán)境下，穩(wěn)定性選擇往往是性能最好的方法之一。

?5.2 遞歸特征消除 Recursive feature elimination (RFE)

遞歸特征消除的主要思想是反復(fù)的構(gòu)建模型（如SVM或者回歸模型）然后選出最好的（或者最差的）的特征（可以根據(jù)系數(shù)來(lái)選），把選出來(lái)的特征放到一遍，然后在剩余的特征上重復(fù)這個(gè)過(guò)程，直到所有特征都遍歷了。這個(gè)過(guò)程中特征被消除的次序就是特征的排序。因此，這是一種尋找最優(yōu)特征子集的貪心算法。

RFE的穩(wěn)定性很大程度上取決于在迭代的時(shí)候底層用哪種模型。例如，假如RFE采用的普通的回歸，沒(méi)有經(jīng)過(guò)正則化的回歸是不穩(wěn)定的，那么RFE就是不穩(wěn)定的；假如采用的是Ridge，而用Ridge正則化的回歸是穩(wěn)定的，那么RFE就是穩(wěn)定的。

Sklearn提供了?RFE?包，可以用于特征消除，還提供了?RFECV?，可以通過(guò)交叉驗(yàn)證來(lái)對(duì)的特征進(jìn)行排序。

from sklearn.feature_selection import RFE
from sklearn.linear_model import LinearRegression

boston = load_boston()
X = boston["data"]
Y = boston["target"]
names = boston["feature_names"]

#use linear regression as the model
lr = LinearRegression()
#rank all features, i.e continue the elimination until the last one
rfe = RFE(lr, n_features_to_select=1)
rfe.fit(X,Y)

print "Features sorted by their rank:"
print sorted(zip(map(lambda x: round(x, 4), rfe.ranking_), names))

Features sorted by their rank: [(1.0, ‘NOX’), (2.0, ‘RM’), (3.0, ‘CHAS’), (4.0, ‘PTRATIO’), (5.0, ‘DIS’), (6.0, ‘LSTAT’), (7.0, ‘RAD’), (8.0, ‘CRIM’), (9.0, ‘INDUS’), (10.0, ‘ZN’), (11.0, ‘TAX’), (12.0, ‘B’), (13.0, ‘AGE’)]

?6 一個(gè)完整的例子

下面將本文所有提到的方法進(jìn)行實(shí)驗(yàn)對(duì)比，數(shù)據(jù)集采用Friedman #1 回歸數(shù)據(jù)（?這篇論文?中的數(shù)據(jù)）。數(shù)據(jù)是用這個(gè)公式產(chǎn)生的：

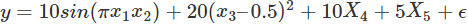
X1到X5是由?單變量分布?生成的，e是?標(biāo)準(zhǔn)正態(tài)變量?N(0,1)。另外，原始的數(shù)據(jù)集中含有5個(gè)噪音變量 X5,…,X10，跟響應(yīng)變量是獨(dú)立的。我們?cè)黾恿?個(gè)額外的變量X11,…X14，分別是X1,…,X4的關(guān)聯(lián)變量，通過(guò)f(x)=x+N(0,0.01)生成，這將產(chǎn)生大于0.999的關(guān)聯(lián)系數(shù)。這樣生成的數(shù)據(jù)能夠體現(xiàn)出不同的特征排序方法應(yīng)對(duì)關(guān)聯(lián)特征時(shí)的表現(xiàn)。

接下來(lái)將會(huì)在上述數(shù)據(jù)上運(yùn)行所有的特征選擇方法，并且將每種方法給出的得分進(jìn)行歸一化，讓取值都落在0-1之間。對(duì)于RFE來(lái)說(shuō)，由于它給出的是順序而不是得分，我們將最好的5個(gè)的得分定為1，其他的特征的得分均勻的分布在0-1之間。

from sklearn.datasets import load_boston
from sklearn.linear_model import (LinearRegression, Ridge, 
                  Lasso, RandomizedLasso)
from sklearn.feature_selection import RFE, f_regression
from sklearn.preprocessing import MinMaxScaler
from sklearn.ensemble import RandomForestRegressor
import numpy as np
from minepy import MINE
np.random.seed(0)
size = 750
X = np.random.uniform(0, 1, (size, 14))
#"Friedamn #1” regression problem
Y = (10 * np.sin(np.pi*X[:,0]*X[:,1]) + 20*(X[:,2] - .5)**2 +
   10*X[:,3] + 5*X[:,4] + np.random.normal(0,1))
#Add 3 additional correlated variables (correlated with X1-X3)
X[:,10:] = X[:,:4] + np.random.normal(0, .025, (size,4))
names = ["x%s" % i for i in range(1,15)]
ranks = {}
def rank_to_dict(ranks, names, order=1):
  minmax = MinMaxScaler()
  ranks = minmax.fit_transform(order*np.array([ranks]).T).T[0]
  ranks = map(lambda x: round(x, 2), ranks)
  return dict(zip(names, ranks ))
lr = LinearRegression(normalize=True)
lr.fit(X, Y)
ranks["Linear reg"] = rank_to_dict(np.abs(lr.coef_), names)
ridge = Ridge(alpha=7)
ridge.fit(X, Y)
ranks["Ridge"] = rank_to_dict(np.abs(ridge.coef_), names)
lasso = Lasso(alpha=.05)
lasso.fit(X, Y)
ranks["Lasso"] = rank_to_dict(np.abs(lasso.coef_), names)
rlasso = RandomizedLasso(alpha=0.04)
rlasso.fit(X, Y)
ranks["Stability"] = rank_to_dict(np.abs(rlasso.scores_), names)
#stop the search when 5 features are left (they will get equal scores)
rfe = RFE(lr, n_features_to_select=5)
rfe.fit(X,Y)
ranks["RFE"] = rank_to_dict(map(float, rfe.ranking_), names, order=-1)
rf = RandomForestRegressor()
rf.fit(X,Y)
ranks["RF"] = rank_to_dict(rf.feature_importances_, names)
f, pval  = f_regression(X, Y, center=True)
ranks["Corr."] = rank_to_dict(f, names)
mine = MINE()
mic_scores = []
for i in range(X.shape[1]):
  mine.compute_score(X[:,i], Y)
  m = mine.mic()
  mic_scores.append(m)
ranks["MIC"] = rank_to_dict(mic_scores, names)
r = {}
for name in names:
  r[name] = round(np.mean([ranks[method][name] 
               for method in ranks.keys()]), 2)
methods = sorted(ranks.keys())
ranks["Mean"] = r
methods.append("Mean")
print "\t%s" % "\t".join(methods)
for name in names:
  print "%s\t%s" % (name, "\t".join(map(str, 
             [ranks[method][name] for method in methods])))

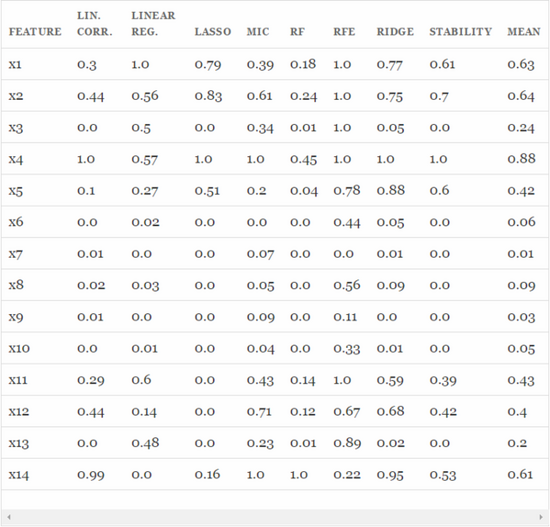
從以上結(jié)果中可以找到一些有趣的發(fā)現(xiàn)：

特征之間存在?線(xiàn)性關(guān)聯(lián)?關(guān)系，每個(gè)特征都是獨(dú)立評(píng)價(jià)的，因此X1,…X4的得分和X11,…X14的得分非常接近，而噪音特征X5,…,X10正如預(yù)期的那樣和響應(yīng)變量之間幾乎沒(méi)有關(guān)系。由于變量X3是二次的，因此X3和響應(yīng)變量之間看不出有關(guān)系（除了MIC之外，其他方法都找不到關(guān)系）。這種方法能夠衡量出特征和響應(yīng)變量之間的線(xiàn)性關(guān)系，但若想選出優(yōu)質(zhì)特征來(lái)提升模型的泛化能力，這種方法就不是特別給力了，因?yàn)樗械膬?yōu)質(zhì)特征都不可避免的會(huì)被挑出來(lái)兩次。

Lasso能夠挑出一些優(yōu)質(zhì)特征，同時(shí)讓其他特征的系數(shù)趨于0。當(dāng)如需要減少特征數(shù)的時(shí)候它很有用，但是對(duì)于數(shù)據(jù)理解來(lái)說(shuō)不是很好用。（例如在結(jié)果表中，X11,X12,X13的得分都是0，好像他們跟輸出變量之間沒(méi)有很強(qiáng)的聯(lián)系，但實(shí)際上不是這樣的）

MIC對(duì)特征一視同仁，這一點(diǎn)上和關(guān)聯(lián)系數(shù)有點(diǎn)像，另外，它能夠找出X3和響應(yīng)變量之間的非線(xiàn)性關(guān)系。

隨機(jī)森林基于不純度的排序結(jié)果非常鮮明，在得分最高的幾個(gè)特征之后的特征，得分急劇的下降。從表中可以看到，得分第三的特征比第一的小4倍。而其他的特征選擇算法就沒(méi)有下降的這么劇烈。

Ridge將回歸系數(shù)均勻的分?jǐn)偟礁鱾€(gè)關(guān)聯(lián)變量上，從表中可以看出，X11,…,X14和X1,…,X4的得分非常接近。

穩(wěn)定性選擇常常是一種既能夠有助于理解數(shù)據(jù)又能夠挑出優(yōu)質(zhì)特征的這種選擇，在結(jié)果表中就能很好的看出。像Lasso一樣，它能找到那些性能比較好的特征（X1，X2，X4，X5），同時(shí)，與這些特征關(guān)聯(lián)度很強(qiáng)的變量也得到了較高的得分。

推薦閱讀

數(shù)據(jù)特征選擇

數(shù)據(jù)特征選擇（二）

《數(shù)據(jù)科學(xué)與人工智能》公眾號(hào)推薦朋友們學(xué)習(xí)和使用Python語(yǔ)言，需要加入Python語(yǔ)言群的，請(qǐng)掃碼加我個(gè)人微信，備注【姓名-Python群】，我誠(chéng)邀你入群，大家學(xué)習(xí)和分享。