高頻面試題 leetcode62/63

作者|萊烏

今天，小萊在leetcode上閑逛，突然眼前一亮，咦！這不是去年來百度二面時(shí)的一道算法題嗎？沒想到在這遇到了。想當(dāng)時(shí)險(xiǎn)些栽到上邊，不過最后千鈞一發(fā)之際，還是想到了解決方法，順利拿到offer 。

畫外音：后來，在小米的面試環(huán)節(jié)中也遇到了此題。

那么，今天小萊就給大家分享下這道動(dòng)態(tài)規(guī)劃題。

題目：

一個(gè)機(jī)器人位于一個(gè) m ×?n 網(wǎng)格的左上角（起始點(diǎn)在下圖中標(biāo)記為“Start” ）。

機(jī)器人每次只能向下或者向右移動(dòng)一步。機(jī)器人試圖達(dá)到網(wǎng)格的右下角（在下圖中標(biāo)記為“Finish”）。

問總共有多少條不同的路徑？

說明：m 和 n 的值均不超過 100。

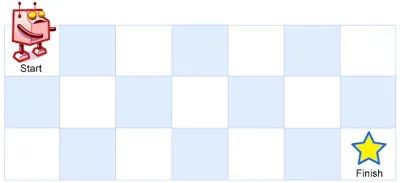
例如，上圖是一個(gè)7 ×?3 的網(wǎng)格。有多少可能的路徑？

畫外音：Leetcode第62題，中等/難度。

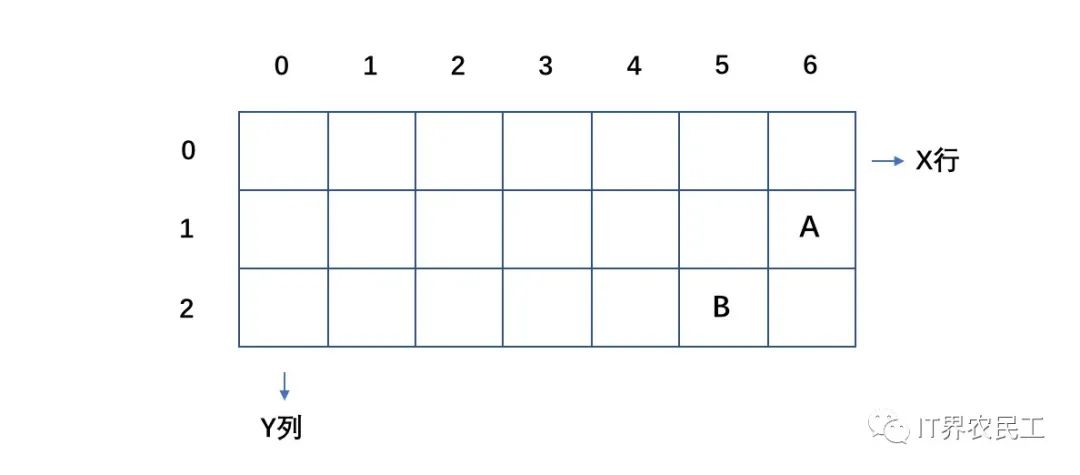
我們由終點(diǎn)位置倒推，從圖中可以看出，想要到達(dá)終點(diǎn)，A、B兩點(diǎn)是必經(jīng)之路。那么，我們想要得到起點(diǎn)到終點(diǎn)的路徑數(shù)，計(jì)算出到達(dá)A、B兩點(diǎn)的路徑總數(shù)不就能夠得出來了嗎？但是A、B兩點(diǎn)的路徑數(shù)如何得出呢。

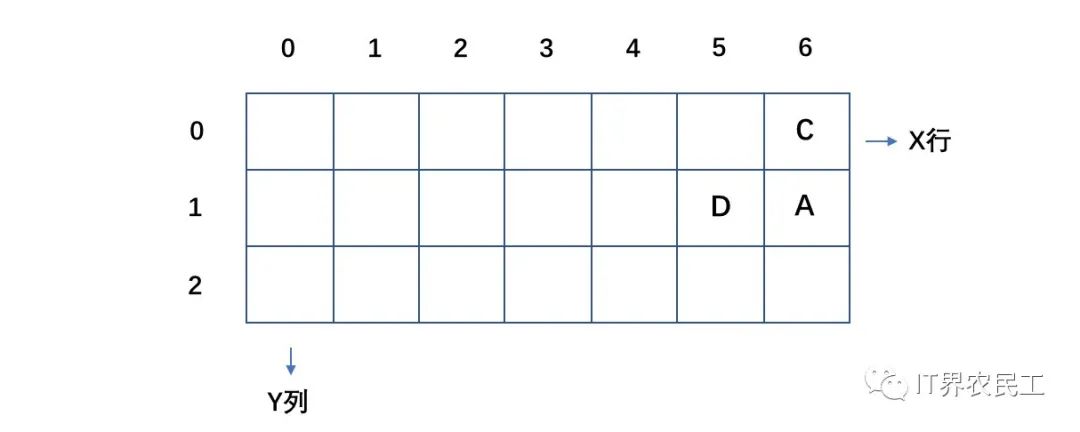
我們不妨再往前推，到達(dá)A點(diǎn)需要經(jīng)過C或者D這兩點(diǎn)，到達(dá)A點(diǎn)的路徑數(shù)可以通過到達(dá)C、D兩點(diǎn)的路徑總數(shù)得知。

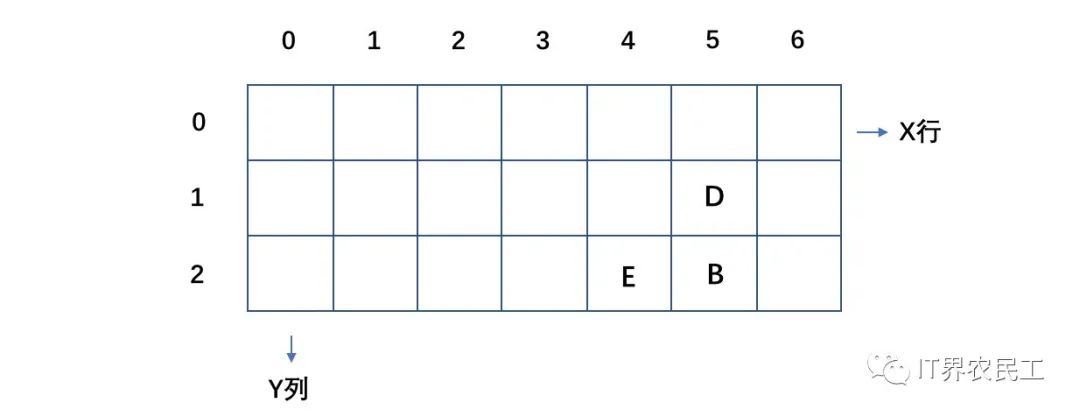
同樣地，到達(dá)B點(diǎn)需要經(jīng)過D點(diǎn)或E點(diǎn)，到達(dá)B點(diǎn)的路徑數(shù)可以通過到達(dá)D、E兩點(diǎn)的路徑總數(shù)得知。

到這，聰明的你有沒有發(fā)現(xiàn)規(guī)律：

每一個(gè)點(diǎn)可到達(dá)路徑數(shù)?= 其相鄰左邊點(diǎn)可到達(dá)路徑數(shù) + 其相鄰上邊點(diǎn)可到達(dá)路徑數(shù)

現(xiàn)在，我們可以回到起點(diǎn)了。

我們可以把m×n方格看作一個(gè)二維數(shù)組，數(shù)組中的每個(gè)元素表示：

起點(diǎn)到該方格的路徑數(shù)

起點(diǎn)到該方格的路徑數(shù)

起點(diǎn)到該方格的路徑數(shù)

（默念三遍！！！）

如下圖中，機(jī)器人到達(dá)第X行（僅第0行）或第Y列（僅第0列）中的任意方格都只有一條路徑。因此，我們將第X行、第Y列的方格元素都置為1。

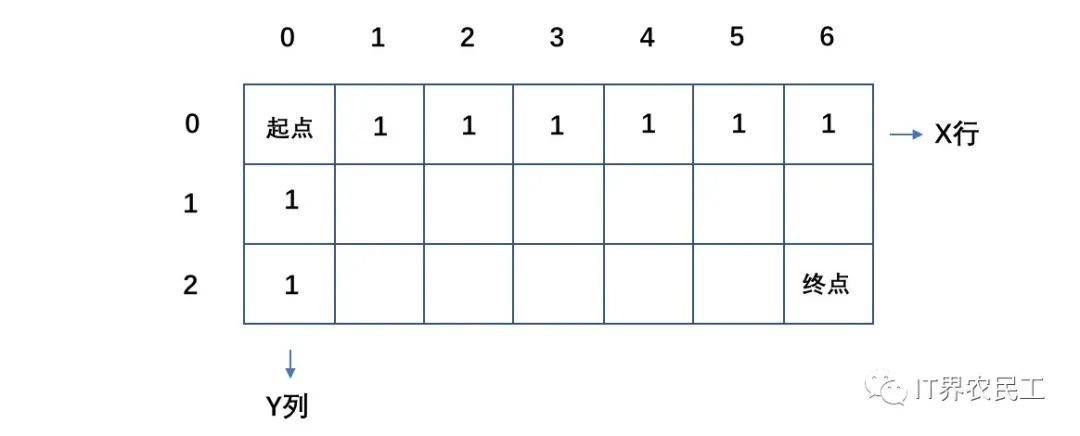
接著，我們繼續(xù)向其它點(diǎn)走。現(xiàn)在分別經(jīng)過路徑一、路徑二走到了S點(diǎn)，因此到達(dá)S點(diǎn)的路徑有2條。

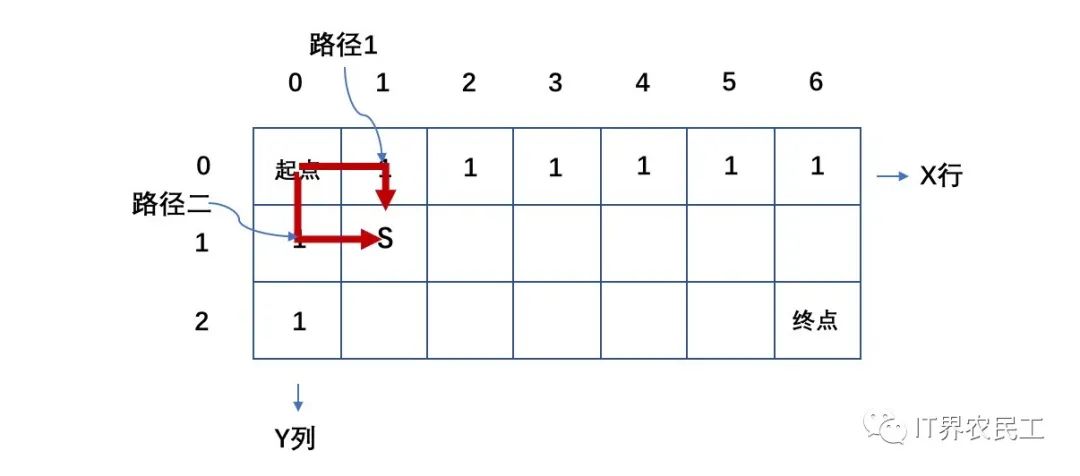
最終，我們得到這樣一張網(wǎng)格，每個(gè)格子里記錄了起點(diǎn)到該格的路徑數(shù)。

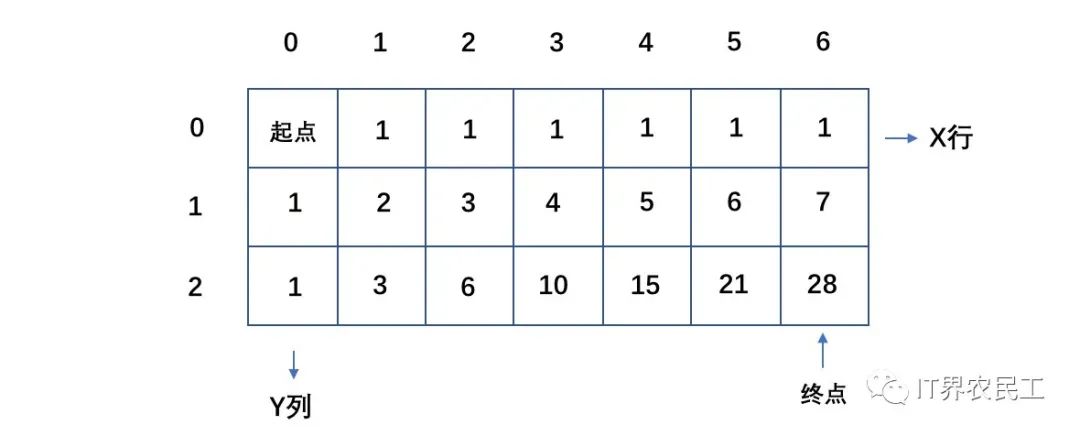
但是如何用代碼表示呢？上邊提到，我們可以將其看作一個(gè)二維數(shù)組v[m][n]。初始時(shí)，將第0行、第0列賦值為1。通過雙層循環(huán)，將目標(biāo)點(diǎn)的上邊元素與左邊元素相加，即可得到當(dāng)前路徑數(shù)。

代碼實(shí)現(xiàn)：

int?uniquePaths(int?m,?int?n){
????if?(m?==?1?||?n?==?1)?{
????????return?1;
????}

????int?i,?j;
????int?v[m][n];

????for?(i?=?1;?i?????????v[i][0]?=?1;
????????for?(j?=?1;?j?????????????v[0][j]?=?1;
????????????v[i][j]?=?v[i][j-1]?+?v[i-1][j];
????????}
????}

????return?v[m-1][n-1];
}

畫外音：本文使用C語言實(shí)現(xiàn)，但是不會(huì)涉及復(fù)雜的語言特性，所以無需擔(dān)心看不懂。另外，代碼實(shí)現(xiàn)小萊在leetcode親測！！！

進(jìn)行到這里，我們就實(shí)現(xiàn)了機(jī)器人從起點(diǎn)到終點(diǎn)暢通無阻情況下所要走的路徑。

你可能注意到了，小萊重點(diǎn)標(biāo)記了下『暢通無阻』這4個(gè)字，這說明還有存在障礙物的情況。那么現(xiàn)在我們就來看看，存在障礙物的情況下，機(jī)器人所走的路徑數(shù)有多少。

畫外音：此題為Leetcode第63題，中等/難度。

如圖中，給定一個(gè)二維數(shù)組obstacleGrid[m][n]，用1來表示障礙物，用0表示空位置。

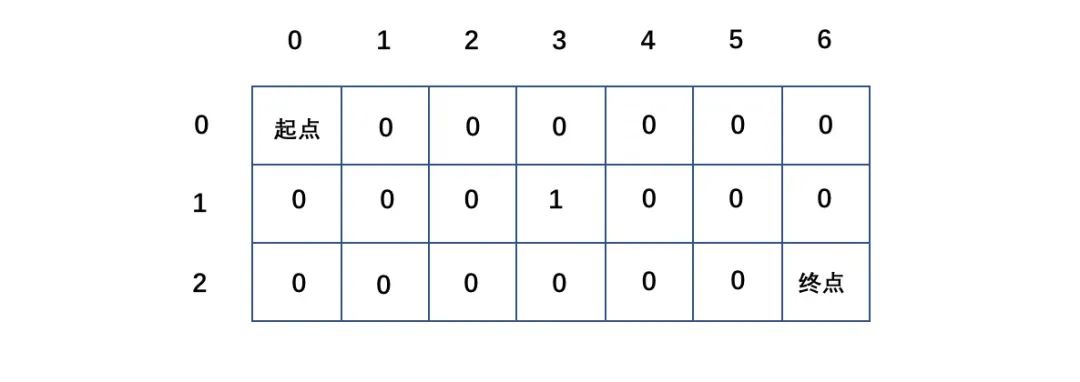
同樣地，我們還是用二維數(shù)組v[m][n]來表示機(jī)器人到達(dá)某個(gè)方格的路徑數(shù)。

但是在處理時(shí)，與無障礙物不同的是，其不再是簡單向右或向下移動(dòng)。初始化和計(jì)算時(shí)要考慮障礙。

這里分為兩種情況：

1、當(dāng)障礙物出現(xiàn)在第0行或第0列，此時(shí)一旦遇到障礙，后續(xù)方格無法到達(dá)，因此后續(xù)行列路徑數(shù)只能為0；

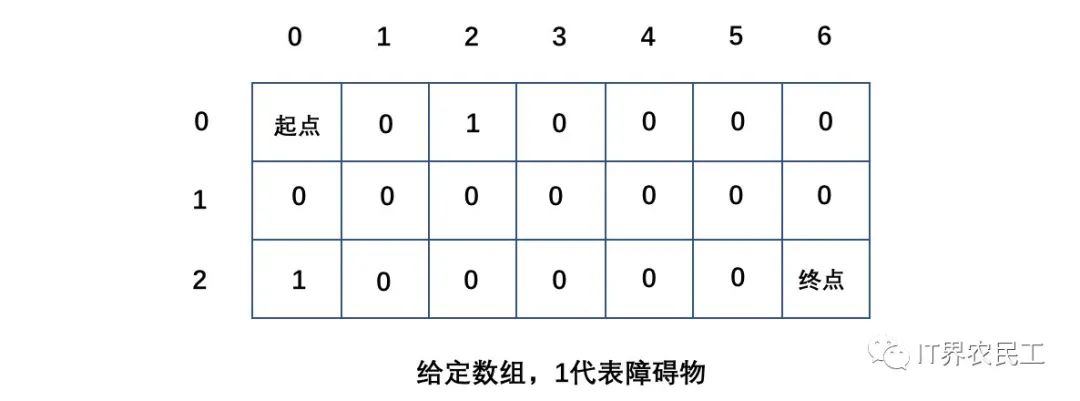
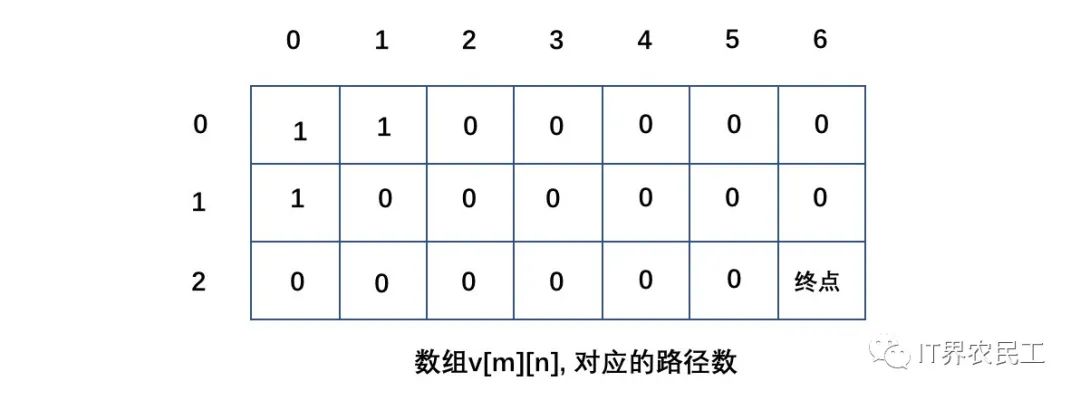
畫外音：這里只給出第0行、第0列路徑數(shù)。

2、當(dāng)障礙物出現(xiàn)在非第0行與第0列的任意位置時(shí)，如果當(dāng)前方格為障礙物時(shí)，可以直接將該方格賦值為0；

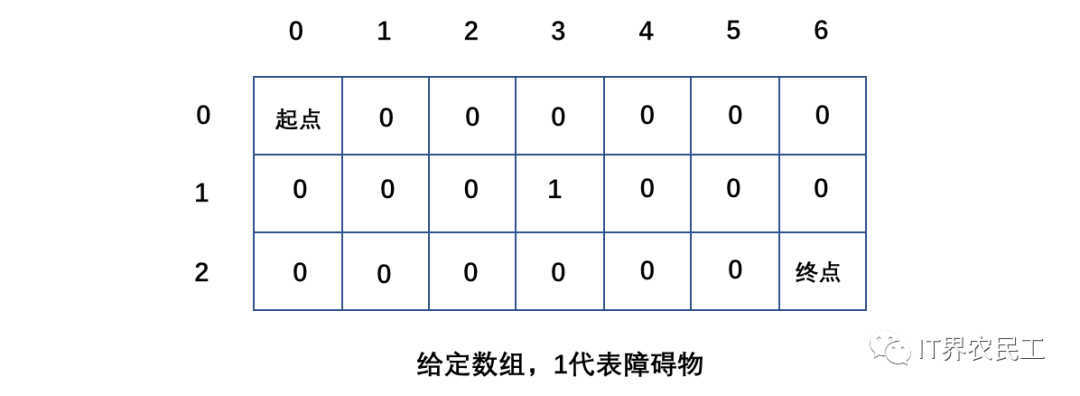
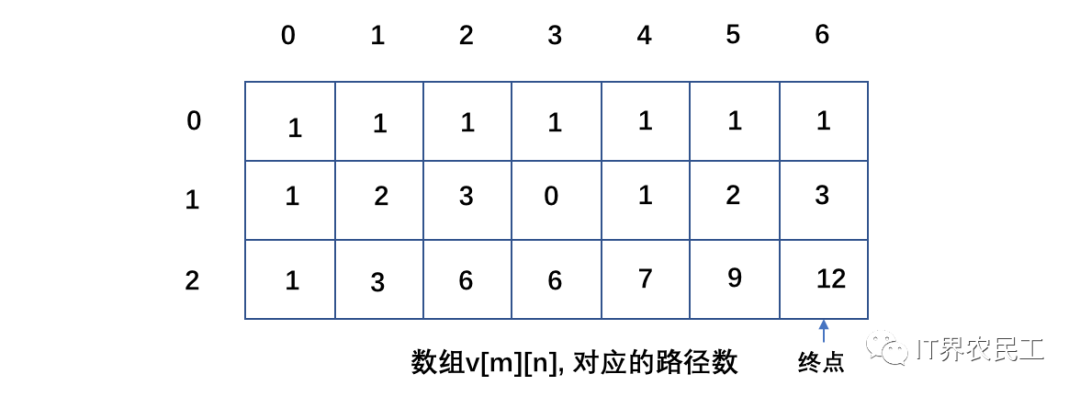
現(xiàn)在我們可以通過代碼來實(shí)現(xiàn)了，首先初始化二維數(shù)組v[m][n]，值默認(rèn)都為0。接著初始化第0行和第0列，當(dāng)未遇到障礙物時(shí)路徑數(shù)為1，否則為0，其后方格的路徑也都為0。然后通過雙層循環(huán)，將目標(biāo)點(diǎn)的上邊元素與左邊元素相加，即可得到當(dāng)前路徑數(shù)（在這個(gè)過程中如果遇到障礙物的話其方格數(shù)為0）。

代碼實(shí)現(xiàn)：

int?uniquePathsWithObstacles(int**?obstacleGrid,?int?obstacleGridSize,?int*?obstacleGridColSize){
????//?m代表行?n代表列
????int?m?=?obstacleGridSize,?n?=?*?obstacleGridColSize;
????if?(obstacleGrid[0][0]?==?1)?{
????????return?0;
????}

????int?i,?j;
????int?v[m][n];
????memset(v,?0,?m?*?n?*?sizeof(int));
????//初始化第一列
????for?(i?=?0;?i?????????if?(obstacleGrid[i][0]?==?1)?{
????????????break;
????????}
????????v[i][0]?=?1;
????}
????//初始化第一行
????for?(j?=?0;?j?????????if?(obstacleGrid[0][j]?==?1)?{
????????????break;
????????}
????????v[0][j]?=?1;
????}

????for?(i?=?1;?i?????????for?(j?=?1;?j?????????????v[i][j]?=?obstacleGrid[i][j]?==?1???0?:?(v[i][j-1]?+?v[i-1][j]);
????????}
????}

????return?v[m-1][n-1];
}

推薦閱讀

1、帥地入職鵝廠的這 180 天里，談一談自己的不足與收獲吧

2、談一談帥地去年艱辛的面試之路吧

3、哭了，帥地手握兩臺(tái) mac ，1000頁的《程序員內(nèi)功修煉》第二版......