經(jīng)典分類：線性判別分析模型！

線性判別分析是一種線性的分類模型。

線性分類模型是指采用直線（或超平面）將樣本直接劃開的模型，其形式可以表示成  的形式，劃分平面可以表示成 。這里可以看出，線性分類模型對于樣本的擬合并不一定是線性的，例如邏輯回歸(外面套了一層sigmod函數(shù))和感知機(外面套了一層激活函數(shù))。

線性判別分析的基本思想是把所有樣本投影到一條直線上，使樣本在這條直線上最容易分類。

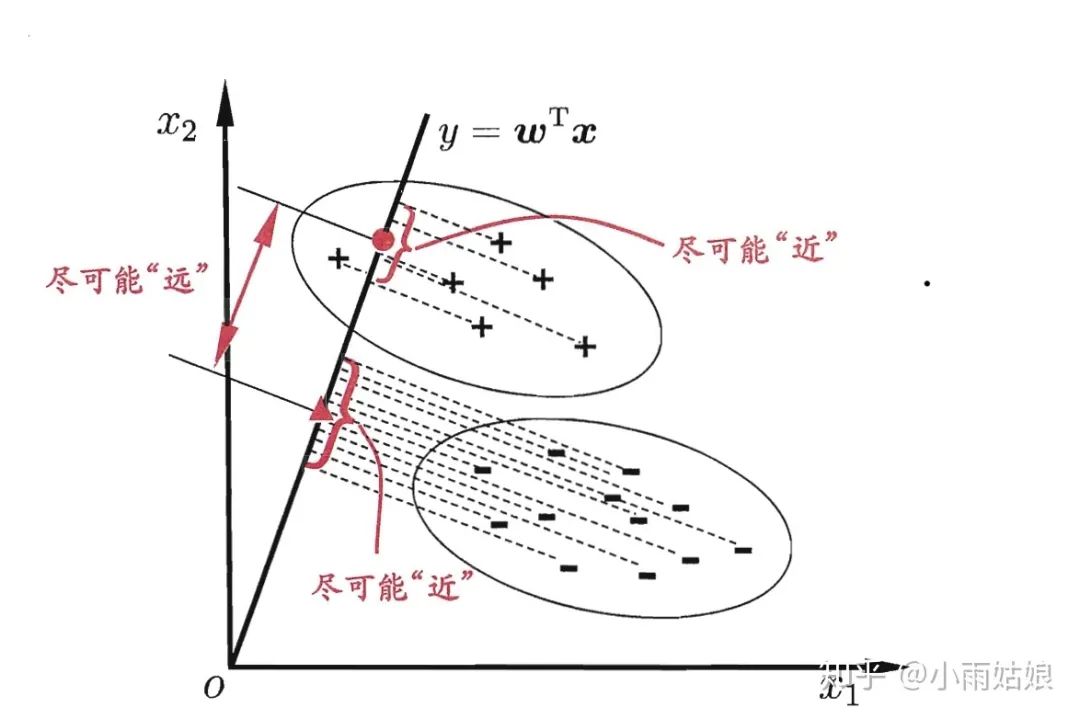
設直線的方向向量為，則樣本在直線上的投影為，如圖：

我們的目標是使兩類樣本的中心點在線上的投影距離大（兩類樣本區(qū)分度高），同時使每一類樣本在線上投影的離散程度盡可能小（類內(nèi)樣本區(qū)分度低）。

令，，分別代表每一類的樣本，每一類樣本的均值向量，每一類樣本的協(xié)方差矩陣。

若將所有樣本都投影到直線上，則兩類樣本的中心點可分別表示為, 。

若將所有樣本都投影到直線上，則兩類樣本的協(xié)方差可表示為, 。

協(xié)方差是什么？協(xié)方差表示的是兩個變量總體誤差的期望。如果兩個變量的變化趨勢一致，則為正值；若相反則為負值；變化趨勢無關(guān)時為0，此時兩個變量獨立。

協(xié)方差矩陣是什么？協(xié)方差矩陣的元素是任意兩個變量之間的協(xié)方差。

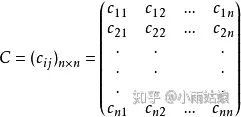
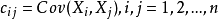
因此我們?nèi)绻寖深悩颖驹谕队昂箅x散程度盡可能小，我們就應該讓他們之間的方差盡可能小。計算每一類元素投影后的方差在做向量化時，中間就是協(xié)方差矩陣（不好意思，下面第二個應該加個轉(zhuǎn)置）。

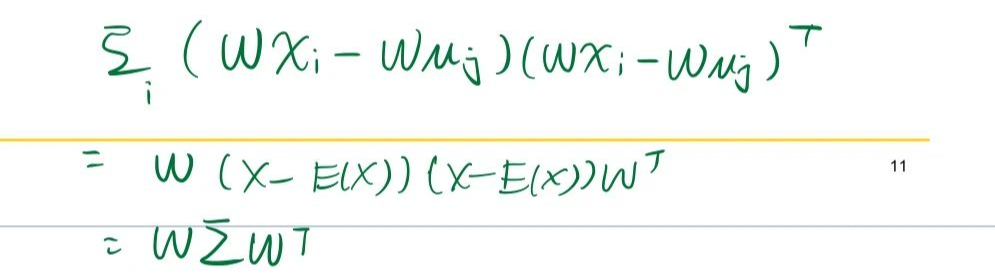
使兩類樣本的中心點在線上的投影距離大，同時使每一類樣本在線上投影的離散程度盡可能小的表達式可以寫為：

對于參數(shù)的優(yōu)化問題可以做如下轉(zhuǎn)換：

因為求的是一個方向向量，所以 同樣也是所求的解，因此我們可以假定

則問題轉(zhuǎn)換為二次規(guī)劃問題：

解得：

最后的判別模型可表示為：

其中b由于不在目標函數(shù)中，所以要手動去找，一般經(jīng)驗方法是：

Python實現(xiàn)如下：

import numpy as np

# 2 dm vectors
x_0 = np.array([[2.95,6.63],[2.53,7.79],[3.57,5.65],[3.16,5.47]])
x_1 = np.array([[2.58,4.46],[2.16,6.22],[3.27,3.52]])

# mean vectors
u_0 = np.mean(x_0, axis=0)
u_1 = np.mean(x_1, axis=0)

# S_w & S_b
S_w = np.cov(x_0, rowvar=False) + np.cov(x_1, rowvar=False)
S_b = np.matmul((u_0 - u_1).reshape(-1,1), (u_0 - u_1).reshape(1,-1))

# Result
w = np.matmul(np.linalg.inv(S_w), (u_0 - u_1))
b = -1 * np.dot((u_0+u_1)/2, w)

實驗結(jié)果：

利用 LDA 進行一個分類的問題：假設一個產(chǎn)品有兩個參數(shù)柔軟性 A 和鋼性 B，來衡量它是否合格，如下圖所示：

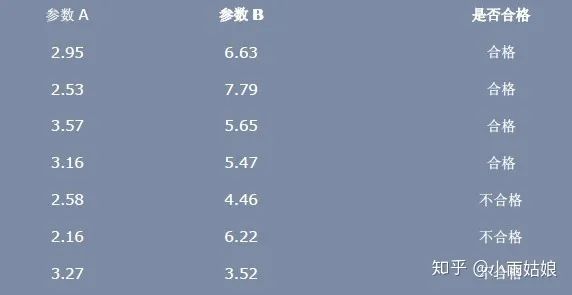
X_0類：

for i in x_0:
    print(np.dot(w , i) + b) 

# 7.908179218783431
# 8.836977507881144
# 11.047547831774281
# 3.8717837839741094

X_1類：

for i in x_1:
    print(np.dot(i , x_0[0]) + b) 

# -39.39697440389426
# -28.96717440389427
# -43.59367440389427