線性判別分析（LDA）原理總結(jié)

重磅干貨，第一時間送達

本文轉(zhuǎn)自：機器學(xué)習(xí)算法那些事

線性判別分析（Linear Discriminant Analysis，以下簡稱LDA）是有監(jiān)督的降維方法，在模式識別和機器學(xué)習(xí)領(lǐng)域中常用來降維。PCA是基于最大投影方差或最小投影距離的降維方法，LDA是基于最佳分類方案的降維方法，本文對其原理進行了詳細總結(jié)。

1. PCA與LDA降維原理對比
2. 二類LDA算法推導(dǎo)

3. 多類LDA算法推導(dǎo)

4. LDA算法流程

5. 正態(tài)性假設(shè)

6. LDA分類算法

7. LDA小結(jié)

1.1    PCA降維原理

PCA是非監(jiān)督式的降維方法，在降維過程中沒有考慮類別的影響，PCA是基于最大投影方差或最小投影距離的降維方法，通俗點說，PCA降維后的樣本集最大程度的保留了初始樣本信息，常用投影距離來描述投影前后樣本的差異信息。

用數(shù)學(xué)公式來闡述這一思想：

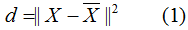
其中原始樣本集（n個m維數(shù)據(jù)）：

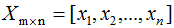
降維后的樣本集（n個k維數(shù)據(jù)）：

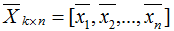
假設(shè)投影變換后的新坐標系（標準正交基）：

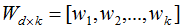
投影前后的樣本關(guān)系：

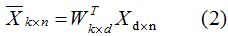
最小化（1）式，并根據(jù)條件（2），可求得最佳的投影坐標系W。給定新的輸入樣本，利用（2）式可求的對應(yīng)的降維樣本。

1.2    LDA降維原理

LDA是有監(jiān)督的降維方法，在降維過程中考慮了類別的影響，LDA是基于最佳分類效果的降維方法。因此，降維后不同類的樣本集具有最大的分類間隔 。

如何描述最大分類間隔，當(dāng)不同類樣本的投影點盡可能遠離且相同類樣本的投影點盡可能接近，則樣本集具有最大分類間隔。我們用類中心間的距離和類的協(xié)方差分別表示不同類的距離和相同類的接近程度。

本節(jié)只考慮二分類的LDA降維，不同類樣本間的投影距離：

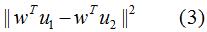
不同類的投影協(xié)方差之和：

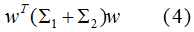
結(jié)合(3)(4)式，得到優(yōu)化目標函數(shù)：

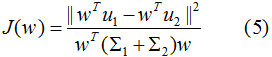
最大化（5）式，得到投影向量w，其中和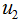分別是兩個類樣本的中心點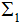，和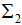分別是兩個類的協(xié)方差。

1.3 PCA與LDA降維應(yīng)用場景對比

若訓(xùn)練樣本集兩類的均值有明顯的差異，LDA降維的效果較優(yōu)，如下圖：

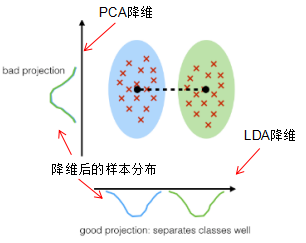
由上圖可知，LDA降維后的二分類樣本集具有明顯差異的樣本分布。

若訓(xùn)練樣本集兩類的均值無明顯的差異，但協(xié)方差差異很大，PCA降維的效果較優(yōu)，如下圖：

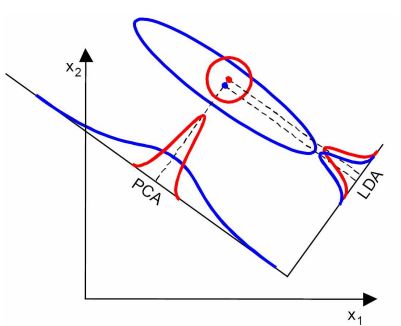
由上圖可知，PCA降維后的二分類樣本分布較LDA有明顯的差異。

假設(shè)二類數(shù)據(jù)集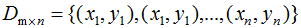，其中xi為m維列向量，我們定義兩類為C1和C2，即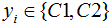，對應(yīng)的樣本集個數(shù)分別為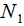和。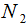

根據(jù)上一節(jié)的LDA的優(yōu)化目標函數(shù)推導(dǎo)投影向量，即最大化目標函數(shù)：

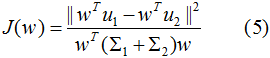
其中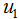和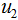為二類的均值向量：

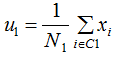
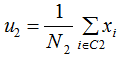
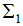和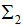為二類的協(xié)方差矩陣：

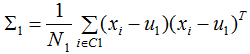
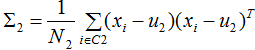
目標函數(shù)轉(zhuǎn)化為：

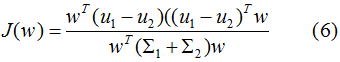
定義類內(nèi)散度矩陣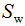和類間散度矩陣：

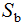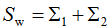
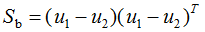
則(6)式等價于：

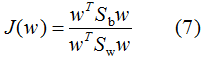
我們對（7）式的分母進行標準化，則（7）式等價于：

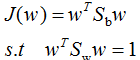
引用拉格朗日乘子法，得：

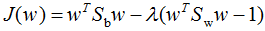
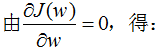
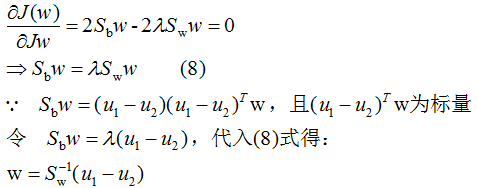
因此，只要求出原始二類樣本的均值和協(xié)方差就可以確定最佳的投影方向w了。

假設(shè)k類數(shù)據(jù)集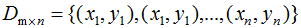，其中xi為m維列向量，我們定義k類為

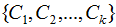，對應(yīng)的樣本集個數(shù)分別為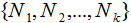。二類樣本數(shù)據(jù)集通過投影向量w降到一維空間，多類樣本數(shù)據(jù)集降到低維空間是一個超平面，假設(shè)投影到低維空間的維度為d，對應(yīng)的基向量矩陣。

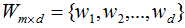因此，多類LDA算法的優(yōu)化目標函數(shù)為：

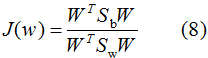
其中類內(nèi)散度矩陣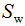和類間散度矩陣：

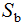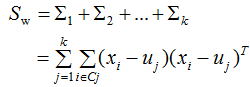
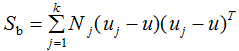
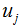為第j類樣本的均值向量，u為所有樣本的均值向量：

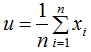
因為(8)式分子分母都是矩陣，常見的一種實現(xiàn)是取矩陣的跡，優(yōu)化目標函數(shù)轉(zhuǎn)化為：

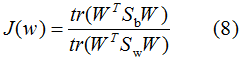
優(yōu)化過程如下：

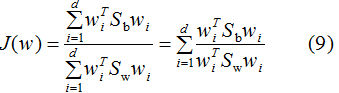
參考二類LDA算法，利用拉格朗日乘子法，得：

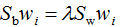
兩邊左乘：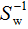

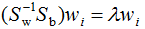
由上式可得LDA的最優(yōu)投影空間是矩陣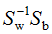最大d個特征值對應(yīng)的特征向量所組成的。

前兩節(jié)推導(dǎo)了LDA算法，現(xiàn)在對LDA算法流程進行總結(jié)，理清一下思路。

假設(shè)k類數(shù)據(jù)集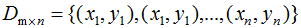，其中xi為m維列向量，我們定義k類為

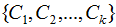，降維后的維度是d。

1）計算每個類樣本的均值向量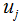和所有數(shù)據(jù)集的均值向量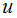

2）計算散度矩陣，包括類內(nèi)散度矩陣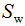和類間散度矩陣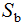

3）計算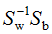的特征向量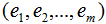和對應(yīng)的特征值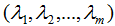

4）選擇d個最大特征值對應(yīng)的矩陣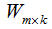，矩陣的每一列表示特征向量

5）對數(shù)據(jù)集D進行降維，得到對應(yīng)的降維數(shù)據(jù)集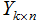，其中。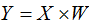

LDA算法對數(shù)據(jù)集進行了如下假設(shè)：

1）數(shù)據(jù)集是服從正態(tài)分布的；

2）特征間是相互獨立的；

3）每個類的協(xié)方差矩陣是相同的；

但是如果不滿足了這三個假設(shè)，LDA算法也能用來分類和降維，因此LDA算法對數(shù)據(jù)集的分布有較好的魯棒性。

前面我們重點分析了LDA算法在降維的應(yīng)用，LDA算法也能用于分類 。LDA假設(shè)各類的樣本數(shù)據(jù)集符合正態(tài)分布，LDA對各類的樣本數(shù)據(jù)進行降維后，我們可以通過最大似然估計去計算各類別投影數(shù)據(jù)的均值和方差，如下式：

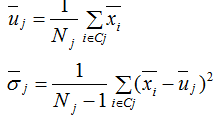
進而得到各個類樣本的概率密度函數(shù)：

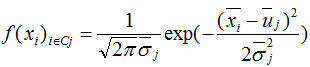
其中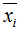為降維后的樣本。

因此對一個未標記的輸入樣本進行LDA分類的步驟：

1） LDA對該輸入樣本進行降維；

2）根據(jù)概率密度函數(shù)，計算該降維樣本屬于每一個類的概率；

3）最大的概率對應(yīng)的類別即為預(yù)測類別。

PCA是基于最大投影方差的降維方法，LDA是基于最優(yōu)分類的降維方法，當(dāng)兩類的均值有明顯差異時，LDA降維方法較優(yōu)；當(dāng)兩類的協(xié)方差有明顯差異時，PCA降維方法較優(yōu)。在實際應(yīng)用中也常結(jié)合LDA和PCA一起使用，先用PCA降維去消除噪聲，再用LDA降維。