【數學筆記】LDA線性判別分析
點擊藍字 關注我們
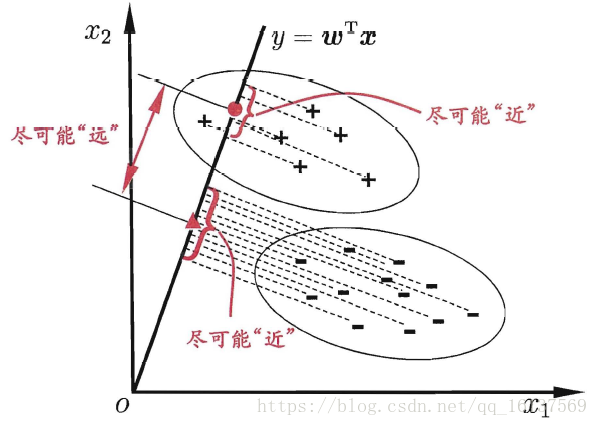
LDA的思想是設法將樣本投影到一條直線上,使得:
同類樣本的投影點盡可能近 異類樣本的投影點盡可能遠
幾何展示
從簡單的二分類LDA分析LDA原理
算法流程
現在我們對LDA降維的流程做一個總結。
輸入:數據集D={(x1,y1),(x2,y2),...,((xm,ym))},其中任意樣本xi為n維向量,yi∈{C1,C2,...,Ck},降維到的維度d。
輸出:降維后的樣本集$D′$
1) 計算類內散度矩陣Sw
2) 計算類間散度矩陣Sb
3) 計算矩陣Sw^?1*Sb
4)計算Sw^?1*Sb的最大的d個特征值和對應的d個特征向量(w1,w2,...wd),得到投影矩陣W
5) 對樣本集中的每一個樣本特征xi,轉化為新的樣本zi=WT*xi
6) 得到輸出樣本集
使用sklearn實現LDA
代碼參數:
class sklearn.discriminant_analysis.LinearDiscriminantAnalysis(solver='svd',shrinkage=None,priors=None,n_components=None,store_covariance=False,tol=0.0001,covariance_estimator=None)
solver : 即求LDA超平面特征矩陣使用的方法。可以選擇的方法有奇異值分解”svd”,最小二乘”lsqr”和特征分解”eigen”。一般來說特征數非常多的時候推薦使用svd,而特征數不多的時候推薦使用eigen。主要注意的是,如果使用svd,則不能指定正則化參數shrinkage進行正則化。默認值是svd。
shrinkage:正則化參數,可以增強LDA分類的泛化能力。如果僅僅只是為了降維,則一般可以忽略這個參數。默認是None,即不進行正則化。可以選擇”auto”,讓算法自己決定是否正則化。當然我們也可以選擇不同的[0,1]之間的值進行交叉驗證調參。注意shrinkage只在solver為最小二乘”lsqr”和特征分解”eigen”時有效。
priors:類別權重,可以在做分類模型時指定不同類別的權重,進而影響分類模型建立。降維時一般不需要關注這個參數。
n_components:進行LDA降維時降到的維數。在降維時需要輸入這個參數。注意只能為[1, 類別數-1]范圍之間的整數。如果不用于降維默認為None。
代碼演示:
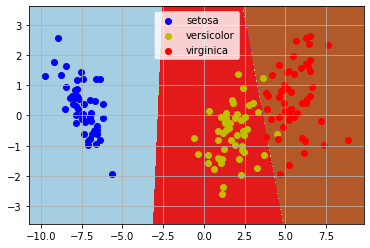
import pandas as pdimport matplotlib.pyplot as pltfrom sklearn.model_selection import train_test_splitfrom sklearn import datasetsfrom sklearn.discriminant_analysis import LinearDiscriminantAnalysisimport numpy as np%matplotlib inlineiris = datasets.load_iris() #典型分類數據模型#這里我們數據統(tǒng)一用pandas處理data = pd.DataFrame(iris.data, columns=iris.feature_names)data['class'] = iris.target#這里只取兩類#data = data[data['class']!=2]#為了可視化方便,這里取兩個屬性為例X = data[data.columns.drop('class')]Y = data['class']#劃分數據集X_train, X_test, Y_train, Y_test =train_test_split(X, Y)lda = LinearDiscriminantAnalysis(n_components=2)lda.fit(X_train, Y_train)#顯示訓練結果print(lda.means_) #中心點print(lda.score(X_test, Y_test)) #score是指分類的正確率print(lda.scalings_)# 樣本縮放比例X_2d = lda.transform(X) #現在已經降到二維X_2d=np.dot(X-lda.xbar_,lda.scalings_)#對于二維數據,我們做個可視化#區(qū)域劃分lda.fit(X_2d,Y)h = 0.02x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1xx, yy = np.meshgrid(np.arange(x_min, x_max, h),np.arange(y_min, y_max, h))Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])Z = Z.reshape(xx.shape)plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)#做出原來的散點圖class1_x = X_2d[Y==0,0]class1_y = X_2d[Y==0,1]l1 = plt.scatter(class1_x,class1_y,color='b',label=iris.target_names[0])class1_x = X_2d[Y==1,0]class1_y = X_2d[Y==1,1]l2 = plt.scatter(class1_x,class1_y,color='y',label=iris.target_names[1])class1_x = X_2d[Y==2,0]class1_y = X_2d[Y==2,1]l3 = plt.scatter(class1_x,class1_y,color='r',label=iris.target_names[2])plt.legend(handles = [l1, l2, l3], loc = 'best')plt.grid(True)plt.show()
輸出:
[[4.99444444 3.40277778 1.45555556 0.25277778][5.94390244 2.75853659 4.24634146 1.3195122 ][6.52571429 2.95428571 5.52285714 2.00571429]]0.9736842105263158[[-1.02533827 -0.39138399][-1.33785618 2.31273541][ 2.41859397 -0.56316402][ 2.3145385 2.41847231]]
LDA算法小結
LDA算法既可以用來降維,又可以用來分類,但是目前來說,主要還是用于降維。在我們進行圖像識別圖像識別相關的數據分析時,LDA是一個有力的工具。下面總結下LDA算法的優(yōu)缺點。
LDA算法的主要優(yōu)點有:
1)在降維過程中可以使用類別的先驗知識經驗,而像PCA這樣的無監(jiān)督學習則無法使用類別先驗知識。
2)LDA在樣本分類信息依賴均值而不是方差的時候,比PCA之類的算法較優(yōu)。
LDA算法的主要缺點有:
1)LDA不適合對非高斯分布樣本進行降維,PCA也有這個問題。
2)LDA降維最多降到類別數k-1的維數,如果我們降維的維度大于k-1,則不能使用LDA。當然目前有一些LDA的進化版算法可以繞過這個問題。
3)LDA在樣本分類信息依賴方差而不是均值的時候,降維效果不好。
4)LDA可能過度擬合數據
參來來源:
https://blog.csdn.net/brucewong0516/article/details/78684005?ops_request_misc=&request_id=&biz_id=102&utm_term=LDA%E5%8E%9F%E7%90%86&utm_medium=distribute.pc_search_result.none-task-blog-2~all~sobaiduweb~default-7-78684005.pc_search_result_before_js
https://blog.csdn.net/qq_25174673/article/details/89301192?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522161442588416780261945728%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&request_id=161442588416780261945728&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~first_rank_v2~rank_v29-14-89301192.pc_search_result_before_js&utm_term=sklearn+%E5%AE%9E%E7%8E%B0LDA
https://blog.csdn.net/ruthywei/article/details/83045288

深度學習入門筆記
微信號:sdxx_rmbj
日常更新學習筆記、論文簡述
