如何進(jìn)行算法的復(fù)雜度分析?

你好，我是彤哥，一個(gè)每天爬二十六層樓還不忘讀源碼的硬核男人。

大家都知道，數(shù)據(jù)結(jié)構(gòu)與算法解決的主要問(wèn)題就是“快”和“省”的問(wèn)題，即如何讓代碼運(yùn)行得更快， 如何讓代碼更節(jié)省存儲(chǔ)空間。

所以，“快”和“省”是衡量一個(gè)算法非常重要的兩項(xiàng)指標(biāo)，也就是我們經(jīng)常聽(tīng)到的時(shí)間復(fù)雜度和空間復(fù)雜度分析。

那么，為什么需要復(fù)雜度分析呢？復(fù)雜度分析的方法論是什么呢？

這就是我們本節(jié)要解決的問(wèn)題。

好了，進(jìn)入今天的學(xué)習(xí)吧。

首先，我們來(lái)思考一個(gè)問(wèn)題：對(duì)于兩個(gè)算法，我們?nèi)绾卧u(píng)判誰(shuí)運(yùn)行得更快，誰(shuí)運(yùn)行時(shí)更節(jié)省內(nèi)存？

你可能會(huì)說(shuō)，這還不簡(jiǎn)單，把這兩個(gè)算法運(yùn)行一遍，統(tǒng)計(jì)下運(yùn)行時(shí)間和占用內(nèi)存不就可以了嗎？

沒(méi)錯(cuò)，這確實(shí)是一種不錯(cuò)的方法，而且它還有個(gè)非常形象的名字：事后統(tǒng)計(jì)法。

但是，這種統(tǒng)計(jì)方法具有非常明顯的問(wèn)題：

1. 不同的輸入對(duì)結(jié)果影響很大

   對(duì)于一些輸入，可能算法A執(zhí)行得更快；對(duì)于另外一些輸入，可能算法B執(zhí)行得更快。比如，我們后面要學(xué)習(xí)的排序算法，輸入的有序性對(duì)于不同的排序算法的影響是完全不同的。

2. 不同的機(jī)器對(duì)結(jié)果影響很大

   對(duì)于同樣的輸入，可能在一臺(tái)機(jī)器上算法A更快，而在另外一臺(tái)機(jī)器上算法B更快。比如，算法A可以利用多核而算法B不能，那么CPU的核數(shù)對(duì)這兩個(gè)算法的影響將截然不同。

3. 數(shù)據(jù)規(guī)模對(duì)結(jié)果影響很大

   當(dāng)數(shù)據(jù)規(guī)模小時(shí)，可能算法A更快，而數(shù)據(jù)規(guī)模變大時(shí)，可能算法B更快。比如，我們后面要學(xué)習(xí)的排序算法，當(dāng)數(shù)據(jù)規(guī)模比較小時(shí)，插入排序反而比歸并排序更快。

所以，我們需要一種可以不用實(shí)際運(yùn)行算法，就可以估計(jì)算法執(zhí)行效率的方法。

這也就是我們所說(shuō)的復(fù)雜度分析。

那么，怎么進(jìn)行復(fù)雜度分析呢？有沒(méi)有什么方法論呢？

還真有，這個(gè)方法論叫做漸近分析法。

漸近分析法，是指將算法執(zhí)行的效率與輸入的規(guī)模進(jìn)行掛鉤，隨著輸入規(guī)模的增大，算法執(zhí)行所需要的時(shí)間（或空間）將呈現(xiàn)一種什么樣的趨勢(shì)，這種趨勢(shì)就叫作漸近，而這種方法就叫作漸近分析法。

概念可能比較拗口，我舉個(gè)簡(jiǎn)單的例子，對(duì)于給定的一個(gè)有序數(shù)組，我要查找其中某個(gè)值所在的位置，比如，查找8這個(gè)元素，有哪些方法呢？

簡(jiǎn)單暴力點(diǎn)的方法，從頭遍歷，查找到該元素即返回。

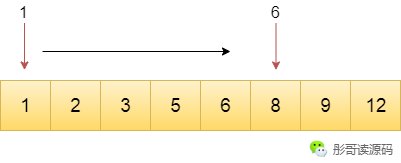
更友好一點(diǎn)的方法，采用二分法，每次定位到數(shù)據(jù)的中間位置，看其值與目標(biāo)值的大小，判斷是在左邊還是右邊繼續(xù)以二分的方式查找。

上面我們舉的例子的輸入規(guī)模是8個(gè)元素的有序數(shù)組，目標(biāo)值為8，使用第二種方法明顯比第一種方法要快很多。

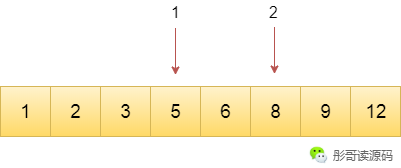
但是，如果查找的目標(biāo)是1呢？

對(duì)于第一種方法，查找一次足矣。

對(duì)于第二種方法，需要查找3次。

此時(shí)，第二種方法又次于第一種方法了。

所以，比較兩個(gè)算法的執(zhí)行效率，不能只考慮到個(gè)別元素，而應(yīng)該顧及到所有元素的感受。

我們以數(shù)學(xué)的方法來(lái)統(tǒng)計(jì)兩種方法的平均執(zhí)行效率，假設(shè)輸入規(guī)模擴(kuò)展到n。

對(duì)于第一種方法，1號(hào)元素查找一次，2號(hào)元素查找兩次，3號(hào)元素查找三次……，而查找每個(gè)元素的概率都是1/n。

所以，它的執(zhí)行效率為：1x1/n + 2x1/n + 3x1/n + ... nx1/n = nx(n+1)/2/n = (n+1)/2。

對(duì)于第二種方法，中間的元素有一個(gè)，查找一次，次中間的元素有兩個(gè)，查找兩次，次次中間的元素有四個(gè)，查找三次...，每次查找的規(guī)模都縮小一半，而查找每個(gè)元素的概率都是1/n。

所以，它的執(zhí)行效率為：1x1x1/n + 2x2x1/n + 4x3x1/n + ... + 2^(log2(n)-2) x (log2(n)-1) x 1/n+ 2^(log2(n)-1) x log2(n) x 1/n = ?

我了個(gè)去，這個(gè)結(jié)果等于多少？

是時(shí)候展現(xiàn)真正的實(shí)力了：

你可能要罵娘了，對(duì)于我一個(gè)小學(xué)畢業(yè)的，難道我沒(méi)辦法學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)與算法了？

No，No，No，肯定不能這么玩，那么，應(yīng)該怎么玩呢？我們下一節(jié)接著講。

本節(jié)，我們從算法執(zhí)行效率方面闡述了為什么需要復(fù)雜度分析，并介紹了復(fù)雜度分析的方法，即漸近分析法，如果嚴(yán)格地遵循漸近分析法，需要大量的數(shù)學(xué)知識(shí)，這無(wú)疑增加了我們分析算法的難度，那么，有沒(méi)有什么更省心地計(jì)算復(fù)雜度的方法呢？