趣說(shuō):如何對(duì)代碼進(jìn)行復(fù)雜度分析
你在學(xué)習(xí)數(shù)據(jù)結(jié)構(gòu)算法的時(shí)候
你的目的就是為了讓代碼
運(yùn)行的速度更加
“快”
占用的空間更加
“少”
那么當(dāng)你看到一段代碼的時(shí)候
你應(yīng)該如何去分析它的運(yùn)行效率?
在此之前
我們來(lái)看看你
不辭辛勞整理的文件夾
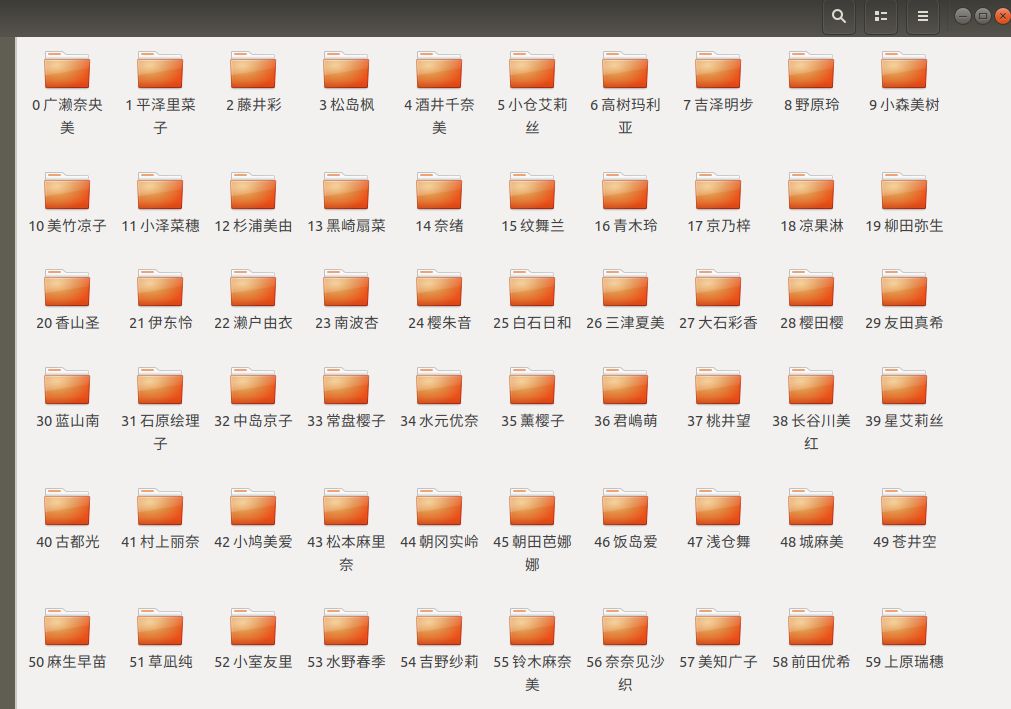
如果要讓你在這個(gè)文件夾里面
讓你找蒼井空老師的教程
你會(huì)怎么找呢?
一種方式是
從第一個(gè)文件到最后一個(gè)文件
依次一個(gè)一個(gè)的查找
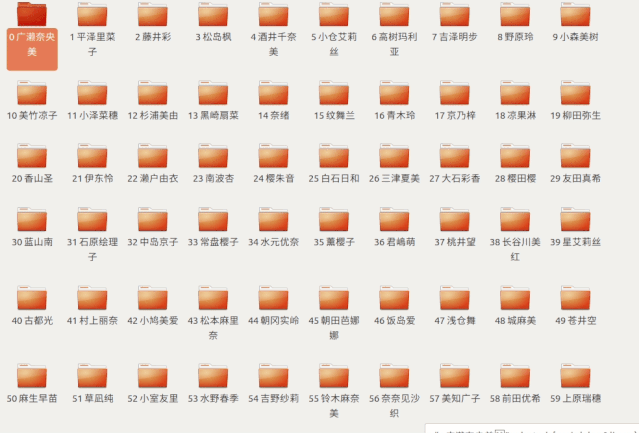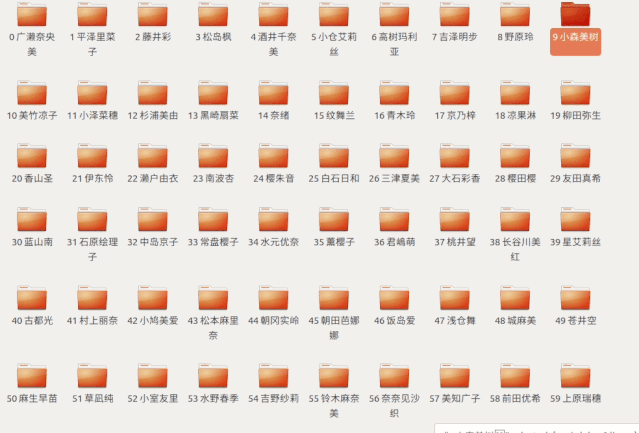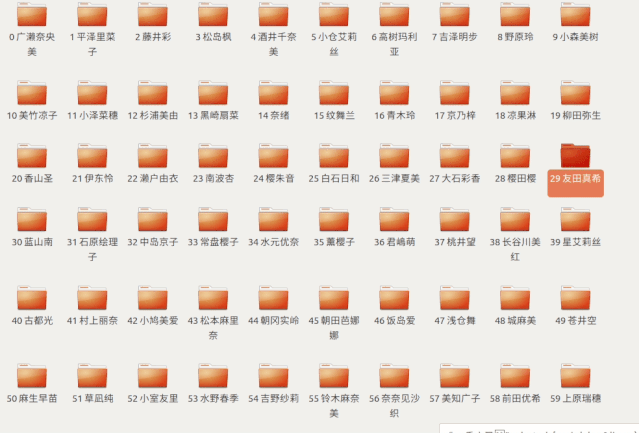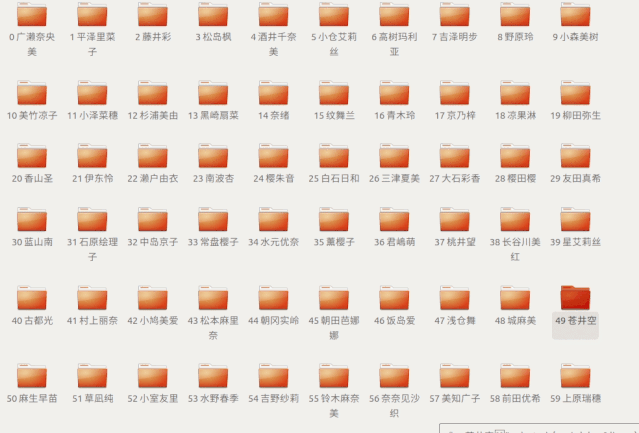
用代碼體現(xiàn)就是這樣
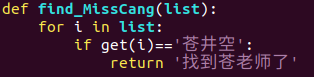
這樣我們找到
第 50?個(gè)文件夾
發(fā)現(xiàn)是蒼井空老師
于是進(jìn)去開(kāi)始觀看了起來(lái)

不過(guò)這種查找效率并不高
另一種查找方式是這樣
咱們先從中間開(kāi)始找
如果發(fā)現(xiàn)小了
就把左邊的都去掉
再在剩下的文件中往中間開(kāi)始找
以此類(lèi)推
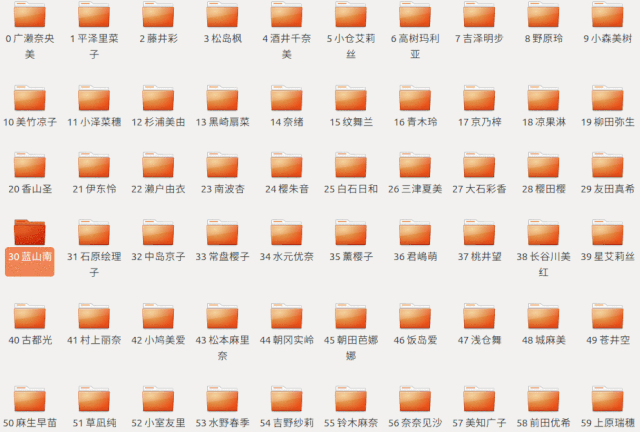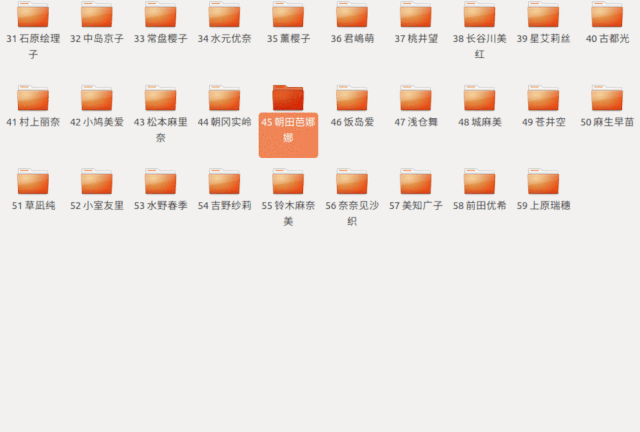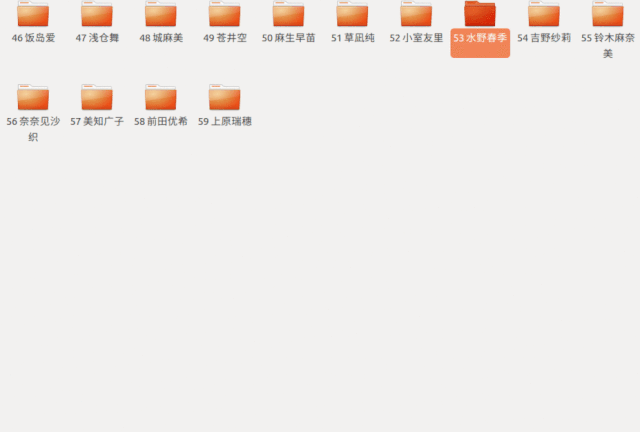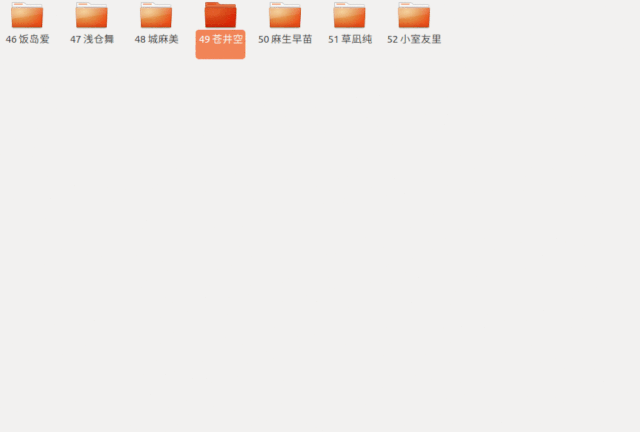
用代碼體現(xiàn)就是這樣
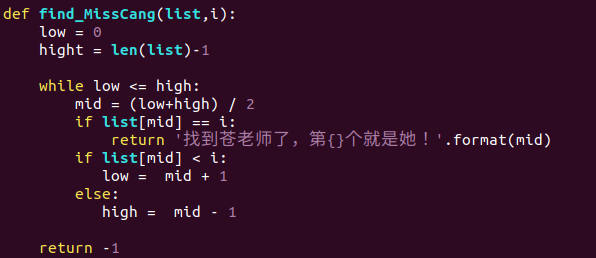
第一種查找方式
我們需要 50 次才找到蒼井空
而第二種方式
我們只需要 4?次就找到了蒼井空
是不是快了很多

其實(shí)第二種方式叫
“二分查找”
在有序列表中
是一種常見(jiàn)的算法
那這和我們要說(shuō)的
代碼復(fù)雜度分析
有什么關(guān)系嘛?

現(xiàn)在我們來(lái)假設(shè)
你的文件夾巨 TM 多
比如有上千萬(wàn)個(gè)文件夾
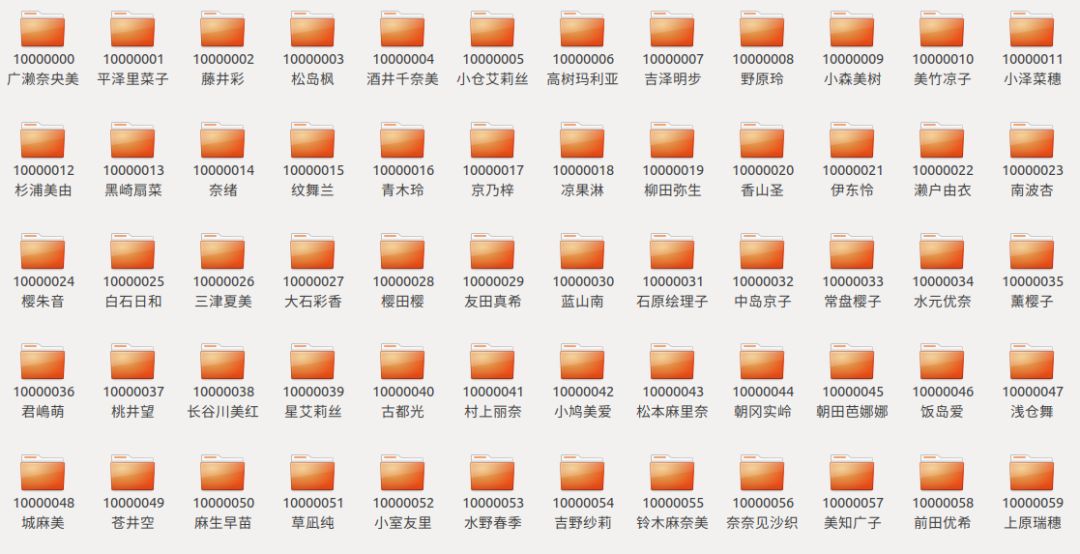
如果你按第一種方式去
找蒼老師的話
你需要找?10000050?次
才能找到她

而你通過(guò)第二種方式去
找蒼老師的話
你只需要 23 次
就能找到它
因?yàn)槎植檎沂且恢闭郯氩樵?/span>
所以是 2 的對(duì)數(shù)
也就是 log10000060
到這里我們就會(huì)發(fā)現(xiàn)
隨著數(shù)據(jù)規(guī)模的增加
代碼的執(zhí)行時(shí)間會(huì)跟著變化

那么如何去表示
不同算法之間的
時(shí)間復(fù)雜度呢?
可以使用
“大胸表示法”

不好意思
說(shuō)錯(cuò)了
是
“大O表示法”
假設(shè)我們的文件夾
有 n 個(gè)這么多
那么第一種查找方式
用大 O 表示時(shí)間復(fù)雜度
就是這樣
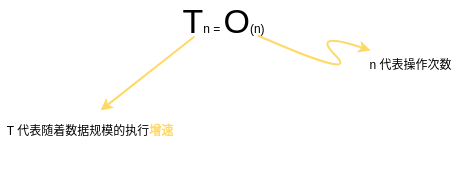
而第二種查找方式
用大 O 表示時(shí)間復(fù)雜度
就是這樣
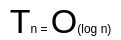
可以看到
執(zhí)行時(shí)間的增速
和操作的次數(shù)成正比
以下這些是較為常見(jiàn)的
代碼時(shí)間復(fù)雜度表示
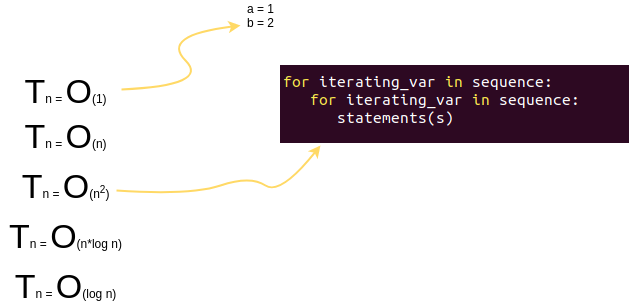
具體來(lái)說(shuō)
復(fù)雜度排序是這樣的
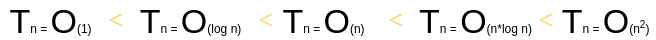
當(dāng)你在分析一段代碼的復(fù)雜度時(shí)
一般情況下
你只要往復(fù)雜的身上整就行了
比如
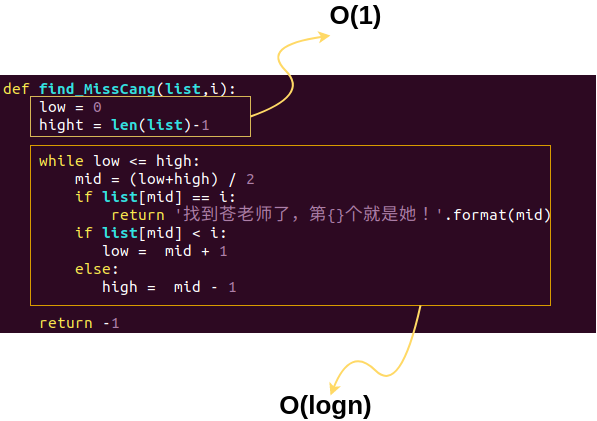
所以這段代碼的復(fù)雜度
就是 O(logn)

最后你可能會(huì)問(wèn)了
不對(duì)啊
如果蒼井空老師的文件夾
在第一個(gè)位置
那使用第一種方式去查找
不就 1 次就能找著了

這時(shí)候效率
不就比二分查找快很多?
這就涉及到不同情況問(wèn)題了
最好的情況就是蒼老師在第 1 個(gè)位置
那么它的復(fù)雜度是 O(1)
最壞的情況就是蒼老師在第 n 個(gè)位置
那么它的復(fù)雜度是 O(n)
這都是在極端情況下的分析
一般我們用一開(kāi)始那樣分析就行了
其它的在特定的情況下
差異比較大才需要考慮
最好最壞以及平均復(fù)雜度相關(guān)的
到時(shí)再具體情況具體分析好了
ok,以上就是
小帥b今天給你帶來(lái)的分享
希望對(duì)你有幫助
那么我們下回再見(jiàn)
peace
推薦閱讀
趣說(shuō):什么是數(shù)據(jù)結(jié)構(gòu)和算法

掃一掃
學(xué)習(xí) Python 沒(méi)煩惱
點(diǎn)個(gè)在看
給點(diǎn)動(dòng)力
