一、IOU(Intersection over Union)

1. 特性(優(yōu)點(diǎn))

IoU就是我們所說的交并比，是目標(biāo)檢測(cè)中最常用的指標(biāo)，在anchor-based的方法，https://zhuanlan.zhihu.com/p/62372897中，他的作用不僅用來確定正樣本和負(fù)樣本，還可以用來評(píng)價(jià)輸出框（predict box）和ground-truth的距離。

1. 可以說它可以反映預(yù)測(cè)檢測(cè)框與真實(shí)檢測(cè)框的檢測(cè)效果。
2. 還有一個(gè)很好的特性就是尺度不變性，也就是對(duì)尺度不敏感（scale invariant）， 在regression任務(wù)中，判斷predict box和gt的距離最直接的指標(biāo)就是IoU。(滿足非負(fù)性；同一性；對(duì)稱性；三角不等性)

import numpy as npdef Iou(box1, box2, wh=False):    if wh == False:  xmin1, ymin1, xmax1, ymax1 = box1  xmin2, ymin2, xmax2, ymax2 = box2    else:  xmin1, ymin1 = int(box1[0]-box1[2]/2.0), int(box1[1]-box1[3]/2.0)  xmax1, ymax1 = int(box1[0]+box1[2]/2.0), int(box1[1]+box1[3]/2.0)  xmin2, ymin2 = int(box2[0]-box2[2]/2.0), int(box2[1]-box2[3]/2.0)  xmax2, ymax2 = int(box2[0]+box2[2]/2.0), int(box2[1]+box2[3]/2.0)    # 獲取矩形框交集對(duì)應(yīng)的左上角和右下角的坐標(biāo)（intersection）    xx1 = np.max([xmin1, xmin2])    yy1 = np.max([ymin1, ymin2])    xx2 = np.min([xmax1, xmax2])    yy2 = np.min([ymax1, ymax2])    # 計(jì)算兩個(gè)矩形框面積    area1 = (xmax1-xmin1) * (ymax1-ymin1)    area2 = (xmax2-xmin2) * (ymax2-ymin2)    inter_area = (np.max([0, xx2-xx1])) * (np.max([0, yy2-yy1]))　#計(jì)算交集面積    iou = inter_area / (area1+area2-inter_area+1e-6) 　#計(jì)算交并比
    return iou

2. 作為損失函數(shù)會(huì)出現(xiàn)的問題(缺點(diǎn))

1. 如果兩個(gè)框沒有相交，根據(jù)定義，IoU=0，不能反映兩者的距離大小（重合度）。同時(shí)因?yàn)閘oss=0，沒有梯度回傳，無法進(jìn)行學(xué)習(xí)訓(xùn)練。
2. IoU無法精確的反映兩者的重合度大小。如下圖所示，三種情況IoU都相等，但看得出來他們的重合度是不一樣的，左邊的圖回歸的效果最好，右邊的最差。

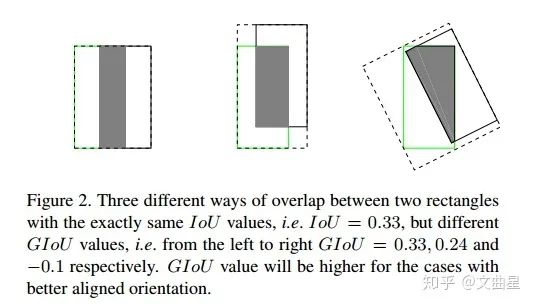
二、GIOU(Generalized Intersection over Union)

1、來源

在CVPR2019中，論文

《Generalized Intersection over Union: A Metric and A Loss for Bounding Box Regression》
https:arxiv.org/abs/1902.09630

的提出了GIoU的思想。由于IoU是比值的概念，對(duì)目標(biāo)物體的scale是不敏感的。然而檢測(cè)任務(wù)中的BBox的回歸損失(MSE loss, l1-smooth loss等）優(yōu)化和IoU優(yōu)化不是完全等價(jià)的，而且 Ln 范數(shù)對(duì)物體的scale也比較敏感，IoU無法直接優(yōu)化沒有重疊的部分。

這篇論文提出可以直接把IoU設(shè)為回歸的loss。

上面公式的意思是：先計(jì)算兩個(gè)框的最小閉包區(qū)域面積_?_(通俗理解：同時(shí)包含了預(yù)測(cè)框和真實(shí)框的最小框的面積)，再計(jì)算出IoU，再計(jì)算閉包區(qū)域中不屬于兩個(gè)框的區(qū)域占閉包區(qū)域的比重，最后用IoU減去這個(gè)比重得到GIoU。

附：

https://github.com/generalized-iou/g-darknet

2、 特性[1]

• 與IoU相似，GIoU也是一種距離度量，作為損失函數(shù)的話，?,滿足損失函數(shù)的基本要求
• GIoU對(duì)scale不敏感
• GIoU是IoU的下界，在兩個(gè)框無線重合的情況下，IoU=GIoU
• IoU取值[0,1]，但GIoU有對(duì)稱區(qū)間，取值范圍[-1,1]。在兩者重合的時(shí)候取最大值1，在兩者無交集且無限遠(yuǎn)的時(shí)候取最小值-1，因此GIoU是一個(gè)非常好的距離度量指標(biāo)。
• 與IoU只關(guān)注重疊區(qū)域不同，GIoU不僅關(guān)注重疊區(qū)域，還關(guān)注其他的非重合區(qū)域，能更好的反映兩者的重合度。

def Giou(rec1,rec2):    #分別是第一個(gè)矩形左右上下的坐標(biāo)    x1,x2,y1,y2 = rec1    x3,x4,y3,y4 = rec2    iou = Iou(rec1,rec2)    area_C = (max(x1,x2,x3,x4)-min(x1,x2,x3,x4))*(max(y1,y2,y3,y4)-min(y1,y2,y3,y4))    area_1 = (x2-x1)*(y1-y2)    area_2 = (x4-x3)*(y3-y4)    sum_area = area_1 + area_2
    w1 = x2 - x1   #第一個(gè)矩形的寬    w2 = x4 - x3   #第二個(gè)矩形的寬    h1 = y1 - y2    h2 = y3 - y4    W = min(x1,x2,x3,x4)+w1+w2-max(x1,x2,x3,x4)    #交叉部分的寬    H = min(y1,y2,y3,y4)+h1+h2-max(y1,y2,y3,y4)    #交叉部分的高    Area = W*H    #交叉的面積    add_area = sum_area - Area    #兩矩形并集的面積
    end_area = (area_C - add_area)/area_C    #閉包區(qū)域中不屬于兩個(gè)框的區(qū)域占閉包區(qū)域的比重    giou = iou - end_area    return giou

三、DIoU(Distance-IoU)[2]

1、來源

DIoU要比GIou更加符合目標(biāo)框回歸的機(jī)制，將目標(biāo)與anchor之間的距離，重疊率以及尺度都考慮進(jìn)去，使得目標(biāo)框回歸變得更加穩(wěn)定，不會(huì)像IoU和GIoU一樣出現(xiàn)訓(xùn)練過程中發(fā)散等問題。論文中

Distance-IoU
https://arxiv.org/pdf/1911.08287.pdf

基于IoU和GIoU存在的問題，作者提出了兩個(gè)問題：
1. 直接最小化anchor框與目標(biāo)框之間的歸一化距離是否可行，以達(dá)到更快的收斂速度？
2. 如何使回歸在與目標(biāo)框有重疊甚至包含時(shí)更準(zhǔn)確、更快？

其中，?，?分別代表了預(yù)測(cè)框和真實(shí)框的中心點(diǎn)，且?代表的是計(jì)算兩個(gè)中心點(diǎn)間的歐式距離。?代表的是能夠同時(shí)包含預(yù)測(cè)框和真實(shí)框的最小閉包區(qū)域的對(duì)角線距離。

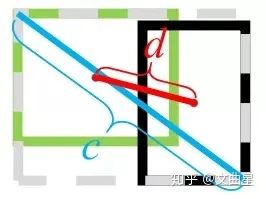
DIoU中對(duì)anchor框和目標(biāo)框之間的歸一化距離進(jìn)行了建模

附：

YOLOV3 DIoU GitHub項(xiàng)目地址
https//github.com/Zzh-tju/DIoU-darknet

2、優(yōu)點(diǎn)

• 與GIoU loss類似，DIoU loss（?）在與目標(biāo)框不重疊時(shí)，仍然可以為邊界框提供移動(dòng)方向。
• DIoU loss可以直接最小化兩個(gè)目標(biāo)框的距離，因此比GIoU loss收斂快得多。
• 對(duì)于包含兩個(gè)框在水平方向和垂直方向上這種情況，DIoU損失可以使回歸非常快，而GIoU損失幾乎退化為IoU損失。
• DIoU還可以替換普通的IoU評(píng)價(jià)策略，應(yīng)用于NMS中，使得NMS得到的結(jié)果更加合理和有效。

實(shí)現(xiàn)代碼：[3]

def Diou(bboxes1, bboxes2):    rows = bboxes1.shape[0]    cols = bboxes2.shape[0]    dious = torch.zeros((rows, cols))    if rows * cols == 0:#        return dious    exchange = False    if bboxes1.shape[0] > bboxes2.shape[0]:        bboxes1, bboxes2 = bboxes2, bboxes1        dious = torch.zeros((cols, rows))        exchange = True    # #xmin,ymin,xmax,ymax->[:,0],[:,1],[:,2],[:,3]    w1 = bboxes1[:, 2] - bboxes1[:, 0]    h1 = bboxes1[:, 3] - bboxes1[:, 1]    w2 = bboxes2[:, 2] - bboxes2[:, 0]    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    area1 = w1 * h1    area2 = w2 * h2
    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2     center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2     center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)    inter_area = inter[:, 0] * inter[:, 1]    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2    outer = torch.clamp((out_max_xy - out_min_xy), min=0)    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)    union = area1+area2-inter_area    dious = inter_area / union - (inter_diag) / outer_diag    dious = torch.clamp(dious,min=-1.0,max = 1.0)    if exchange:        dious = dious.T    return dious

四、CIoU(Complete-IoU)

論文考慮到bbox回歸三要素中的長(zhǎng)寬比還沒被考慮到計(jì)算中，因此，進(jìn)一步在DIoU的基礎(chǔ)上提出了CIoU。其懲罰項(xiàng)如下面公式：

其中?是權(quán)重函數(shù)，

而?用來度量長(zhǎng)寬比的相似性，定義為

完整的 CIoU 損失函數(shù)定義：

最后，CIoU loss的梯度類似于DIoU loss，但還要考慮?的梯度。在長(zhǎng)寬在?的情況下，?的值通常很小，會(huì)導(dǎo)致梯度爆炸，因此在?實(shí)現(xiàn)時(shí)將替換成1。[4]

實(shí)現(xiàn)代碼：[5]

def bbox_overlaps_ciou(bboxes1, bboxes2):    rows = bboxes1.shape[0]    cols = bboxes2.shape[0]    cious = torch.zeros((rows, cols))    if rows * cols == 0:        return cious    exchange = False    if bboxes1.shape[0] > bboxes2.shape[0]:        bboxes1, bboxes2 = bboxes2, bboxes1        cious = torch.zeros((cols, rows))        exchange = True
    w1 = bboxes1[:, 2] - bboxes1[:, 0]    h1 = bboxes1[:, 3] - bboxes1[:, 1]    w2 = bboxes2[:, 2] - bboxes2[:, 0]    h2 = bboxes2[:, 3] - bboxes2[:, 1]
    area1 = w1 * h1    area2 = w2 * h2
    center_x1 = (bboxes1[:, 2] + bboxes1[:, 0]) / 2    center_y1 = (bboxes1[:, 3] + bboxes1[:, 1]) / 2    center_x2 = (bboxes2[:, 2] + bboxes2[:, 0]) / 2    center_y2 = (bboxes2[:, 3] + bboxes2[:, 1]) / 2
    inter_max_xy = torch.min(bboxes1[:, 2:],bboxes2[:, 2:])    inter_min_xy = torch.max(bboxes1[:, :2],bboxes2[:, :2])    out_max_xy = torch.max(bboxes1[:, 2:],bboxes2[:, 2:])    out_min_xy = torch.min(bboxes1[:, :2],bboxes2[:, :2])
    inter = torch.clamp((inter_max_xy - inter_min_xy), min=0)    inter_area = inter[:, 0] * inter[:, 1]    inter_diag = (center_x2 - center_x1)**2 + (center_y2 - center_y1)**2    outer = torch.clamp((out_max_xy - out_min_xy), min=0)    outer_diag = (outer[:, 0] ** 2) + (outer[:, 1] ** 2)    union = area1+area2-inter_area    u = (inter_diag) / outer_diag    iou = inter_area / union    with torch.no_grad():        arctan = torch.atan(w2 / h2) - torch.atan(w1 / h1)        v = (4 / (math.pi ** 2)) * torch.pow((torch.atan(w2 / h2) - torch.atan(w1 / h1)), 2)        S = 1 - iou        alpha = v / (S + v)        w_temp = 2 * w1    ar = (8 / (math.pi ** 2)) * arctan * ((w1 - w_temp) * h1)    cious = iou - (u + alpha * ar)    cious = torch.clamp(cious,min=-1.0,max = 1.0)    if exchange:        cious = cious.T    return cious

五、損失函數(shù)在YOLOv3上的性能(論文效果)

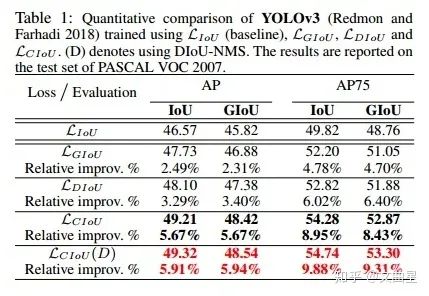
目標(biāo)檢測(cè)算法之AAAI 2020 DIoU Loss 已開源(YOLOV3漲近3個(gè)點(diǎn))
https://cloud.tencent.com/developer/article/1558533

參考

1. https://zhuanlan.zhihu.com/p/57863810
2. DIoU參考?https://mp.weixin.qq.com/s/7E2xG1LUQZGWvUee1llmsA
3. DIOU代碼實(shí)現(xiàn)?https://blog.csdn.net/TJMtaotao/article/details/103317267
4. AAAI 2020 | DIoU 和 CIoU：IoU 在目標(biāo)檢測(cè)中的正確打開方式 https://bbs.cvmart.net/articles/1396
5. https://blog.csdn.net/TJMtaotao/article/details/103317267

—完—
添加號(hào)主微信，備注“2020nn”領(lǐng)取2020最新版《神經(jīng)網(wǎng)絡(luò)與深度學(xué)習(xí)》中文版及課件。