DIoU 和 CIoU 的原理與代碼
本篇接著上篇 交并比(IoU 與 GIoU 原理與實(shí)現(xiàn)) 繼續(xù),上篇介紹了 IoU 和 GIoU,本篇分享 DIoU 和 CIoU 的原理與實(shí)現(xiàn)。
DIoU 原理與實(shí)現(xiàn)
DIoU 原理
GIoU 雖然解決了 IoU 的一些問題,但是它并不能直接反映預(yù)測(cè)框與目標(biāo)框之間的距離,DIoU(Distance-IoU)即可解決這個(gè)問題,它將兩個(gè)框之間的重疊度、距離、尺度都考慮了進(jìn)來。DIoU的計(jì)算公式如下:
其中, 和 分別代表兩個(gè)框的中心點(diǎn), 代表兩個(gè)中心點(diǎn)之間的歐式距離, 代表兩個(gè)圖像的最小外接矩形的對(duì)角線,如圖 1 所示。
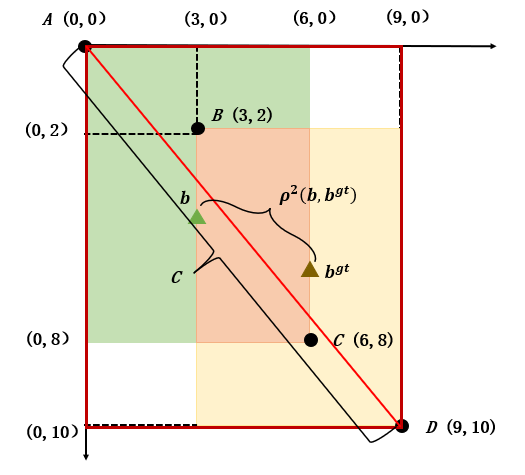
DIoU 相較于其他兩種計(jì)算方法的優(yōu)點(diǎn)是:
DIoU 可直接最小化兩個(gè)框之間的距離,所以作為損失函數(shù)時(shí) Loss 收斂更快。
在兩個(gè)框完全上下排列或左右排列時(shí),沒有空白區(qū)域,此時(shí) GIoU 幾乎退化為了 IoU,但是 DIoU 仍然有效。
所以,DIoU 在完善圖像重疊度的計(jì)算功能的基礎(chǔ)上,實(shí)現(xiàn)了對(duì)圖形距離的考量,但仍無法對(duì)圖形長寬比的相似性進(jìn)行很好的表示。
DIoU 計(jì)算
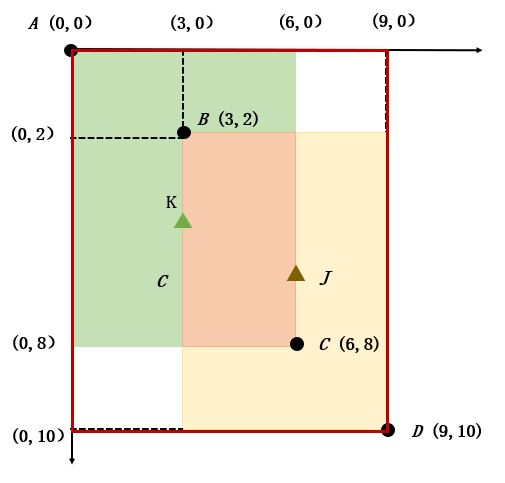
在圖 2 中,通過計(jì)算可得,中心點(diǎn) 、中心點(diǎn) 的坐標(biāo)分別為:
此時(shí)的 DIoU 計(jì)算公式為:
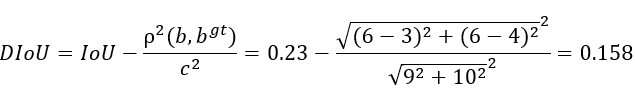
DIoU 實(shí)現(xiàn)
代碼如下:
import numpy as np
import IoU
# box : [左上角x坐標(biāo),左上角y坐標(biāo),右下角x坐標(biāo),右下角y坐標(biāo)]
box1 = [0, 0, 6, 8]
box2 = [3, 2, 9, 10]
# DIoU
def DIoU(box1, box2):
# 計(jì)算對(duì)角線長度 C
x1, y1, x2, y2 = box1
x3, y3, x4, y4 = box2
# numpy.sqrt() 函數(shù)計(jì)算給定數(shù)組中每個(gè)元素的平方根。
C = np.sqrt((max(x2, x4) - min(x1, x3)) ** 2 +
(max(y2, y4) - min(y3, y1)) ** 2)
print('C: ', C)
# box1 中心點(diǎn)x坐標(biāo): x2 - (x2 - x1) / 2
point1_x, point1_y = (x2 + x1) / 2, (y2 + y1) / 2
# box2 中心點(diǎn)
point2_x, point2_y = (x4 + x3) / 2, (y4 + y3) / 2
# 計(jì)算中心點(diǎn)間距 D
D = np.sqrt((point2_x - point1_x) ** 2 +
(point2_y - point1_y) ** 2)
# 計(jì)算IoU,調(diào)用IoU(box1, box2)函數(shù)
iou = IoU(box1, box2)
diou = iou - (D ** 2 / C ** 2)
return diou
print(DIoU(box1,box2))
CIoU 原理與實(shí)現(xiàn)
CIoU 原理
CIoU 的全稱為 Complete IoU,它在 DIoU 的基礎(chǔ)上,還同時(shí)考慮兩個(gè)矩形的長寬比,也就是形狀的相似性。CIoU 的計(jì)算公式為:
其中, 是權(quán)重函數(shù),而 用來度量長寬比的相似性。計(jì)算公式為:
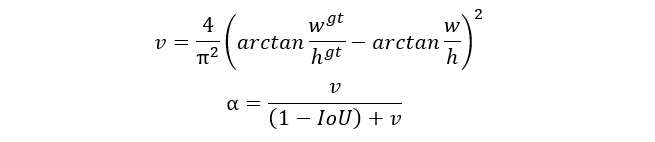
可以看出,CIoU 就是在 DIoU 的基礎(chǔ)上,增加了圖像相似性的影響因子,因此可以更好地反映兩個(gè)框之間的差異性。
還需要注意的一點(diǎn)是,在使用 CIoU 作為 Loss 的時(shí)候, 的梯度同樣會(huì)參與反向傳播的計(jì)算,其中:
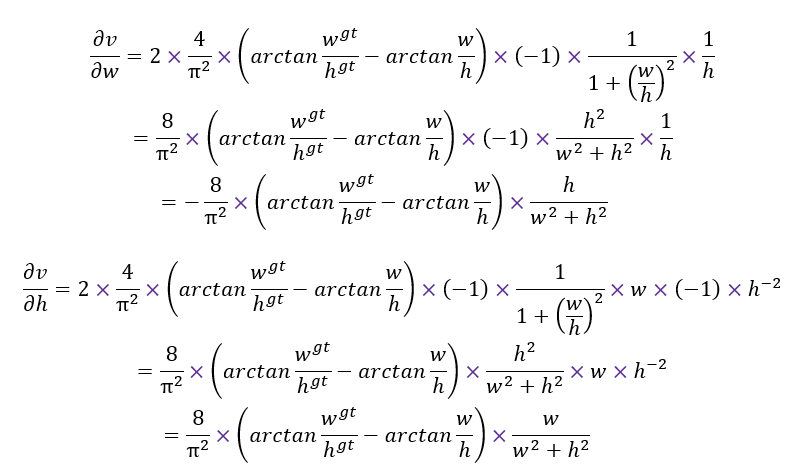
如果矩形的 和 均小于1, 的值則會(huì)很小,這樣很容易出現(xiàn)梯度爆炸的現(xiàn)象,所以在計(jì)算 的梯度時(shí),直接把 當(dāng)做 1 來計(jì)算。論文里會(huì)在 關(guān)于 和 的偏導(dǎo)數(shù)上加負(fù)號(hào)。
至此,IoU 終于實(shí)現(xiàn)了對(duì)兩個(gè)圖像之間的重疊比例、圖形距離、形狀相似度(矩形長寬比)的綜合度量。
CIoU 計(jì)算
繼續(xù)以圖 2 為例,中心點(diǎn) 、中心點(diǎn) 的坐標(biāo)分別為:
此時(shí) CIoU 的計(jì)算公式為:
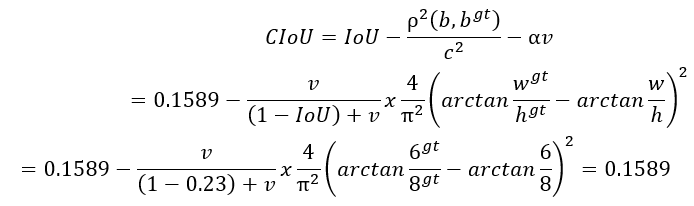
由于最開始設(shè)定的兩個(gè)矩形的形狀相同,計(jì)算所得的形狀懲罰項(xiàng)為 0,因此此時(shí) CIoU=DIoU 。由此可見,兩個(gè)形狀差別越大,CIoU 相較于 DIoU 越小。
CIoU 實(shí)現(xiàn)
代碼如下:
import numpy as np
import IoU
import DIoU
# box : [左上角x坐標(biāo),左上角y坐標(biāo),右下角x坐標(biāo),右下角y坐標(biāo)]
box1 = [0, 0, 6, 8]
box2 = [3, 2, 9, 10]
# CIoU
def CIoU(box1, box2):
x1, y1, x2, y2 = box1
x3, y3, x4, y4 = box2
# box1的寬:box1_w,box1的高:box1_h,
box1_w = x2 - x1
box1_h = y2 - y1
# box2的寬:box2_w,box2的高:box2_h,
box2_w = x4 - x3
box2_h = y4 - y3
iou = IoU(box1, box2)
diou = DIoU(box1, box2)
# v用來度量長寬比的相似性
v = (4 / (np.pi) ** 2) * (np.arctan(int(box2_w / box2_h)) - np.arctan(int(box1_w / box1_h)))
# α是權(quán)重函數(shù)
a = v / ((1 + iou) + v)
ciou = diou - a * v
return ciou
print(CIoU(box1, box2))
今天分享了 DIoU 和 CIoU 的原理和代碼,后臺(tái)回復(fù) IoU,即可獲得 IoU、GIoU、DIoU 和 CIoU 的代碼。
最后祝大家有所進(jìn)步!
參考文獻(xiàn)
[1] 理解梯度:https://www.cnblogs.com/zzzzy/p/8505150.html
[2] Generalized Intersection over Union:https://arxiv.org/pdf/1902.09630.pdf
[3] Distance-IoU Loss: https://arxiv.org/pdf/1911.08287.pdf
[4] 交并比(IoU 與 GIoU 原理與實(shí)現(xiàn))
