免费操屄,国内精品久久久久久久久久98,大香蕉啪啪网,在线综合视频,欧美成人怡红院,一本色道无码道DVD在线播放,欧美v亚洲v日韩v最新在线,日韩乱码一区二区

為了進一步了解非線性控制，我一直在嘗試一種非常有效的方法，稱為軌跡優(yōu)化。設(shè)置完基本代碼后，就可以很容易地將其應(yīng)用于各種系統(tǒng)。這是在無人機上運行的一個有趣示例：

無人機翻轉(zhuǎn)表演

在看完Starship SN15發(fā)射后，我決定進行一些動力學(xué)估算，以檢驗我的2D模擬玩具是否能執(zhí)行翻轉(zhuǎn)并自行著陸。令我興奮的是，經(jīng)過一番細心的研究，它運行得很好。但是真正令我驚訝的是當(dāng)我與實際的著陸畫面并排播放輸出時：它的軌跡非常完美。而且編寫整個程序和優(yōu)化時我并沒有參考視頻或其他明確的計時信息。

對我而言有兩種可能：1、我非常幸運，2、SpaceX在其實際系統(tǒng)上運行了非常相似的優(yōu)化。這是一個非常有趣的東西，希望能為進入火箭回收后面的魔法打開一扇窗戶。在開始編寫代碼之前，可能最好先解釋一下軌跡優(yōu)化的理論（但如果您愿意，也可以直接跳轉(zhuǎn)至代碼）。

軌跡優(yōu)化：“最優(yōu)軌跡”意味著什么？

在這種情況下，“最佳”表示通常的含義：“好”，“最佳”，“理想”等。舉一個簡單的例子，假設(shè)您想走過整個房間到達冰箱：您可以選擇看似無數(shù)的路線，但是以某種方式只能選擇其中一條路線。

兩條軌跡的例子

應(yīng)該很容易看到有好路線和差路線，但是實際上定義好軌跡還是差軌跡的是什么呢？這就是“成本”概念進入的地方。如果您有機器學(xué)習(xí)的經(jīng)驗，那么這基本上是相同的概念。您運行優(yōu)化以最小化成本函數(shù)。在我們的冰箱示例中，成本函數(shù)是什么？一個簡單的方法就是走我們的路。現(xiàn)在可以要求計算機在您和冰箱之間找到一條長度最短的路徑。

選擇成本函數(shù)

這可行，但有一些細微的缺陷。想象一下，您和冰箱之間有一個死亡陷阱。我們的“查找最小長度”算法將使您正確地進行操作，我認為您可能會認為這并不是真正的最佳選擇。

可能更好的成本函數(shù)（以及我在Starship著陸代碼中主要使用的函數(shù)）基于“努力”。假設(shè)您在地板上向前邁出一步需要您付出1點努力，而經(jīng)過死亡之坑?則需要您花費1000點努力。這更好地匹配了我們認為是最佳與非最佳的條件：

約束

很少有優(yōu)化問題可以在沒有很多約束的情況下完成，這是一些“邏輯”問題，可以解決我們的冰箱問題。

其他資料

這是軌跡優(yōu)化的核心。通過最小化某些成本函數(shù)并保持一組約束來優(yōu)化點之間的軌跡。這里有一些很好的資源，它們在數(shù)學(xué)方面會更深入：

https://www.youtube.com/watch?v=wlkRYMVUZTs

為火箭著陸進行編碼！

現(xiàn)在到有趣的東西上。有一些很棒的庫可以遍歷方程式并進行優(yōu)化工作，因此真正的“藝術(shù)”在于向解釋器提出正確的問題。下面是一個指向collab notebook的鏈接，可讓您在瀏覽器中運行全部代碼：

https://colab.research.google.com/drive/18MVtu4reVJLBE1RXByQEmu0O9aLXlMHz?usp=sharing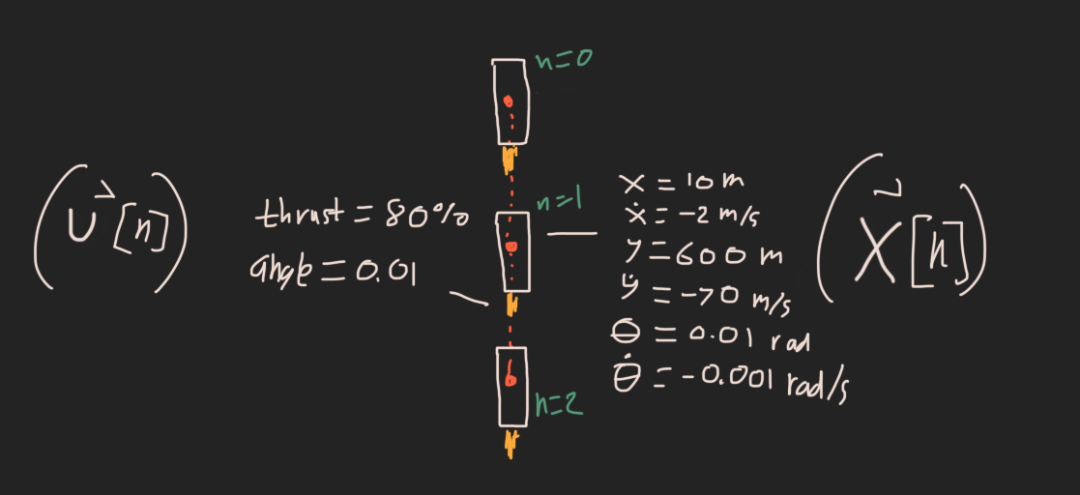

軌跡

時間被切成0.04s的塊，并在每個步驟中生成了火箭狀態(tài)和控制狀態(tài)的變量。這導(dǎo)致沿路徑產(chǎn)生一堆離散點，這些點比較容易處理，然后嘗試為整個對象提出封閉形式的解決方案。

由三個點和沿著該軌跡的狀態(tài)組成的軌跡的示例

火箭狀態(tài)向量：x[n] = [x, x_dot, y, y_dot, theta, theta_dot]

控制狀態(tài)向量：u[n] = [thrust_mag, thrust_angle]

生成步驟和優(yōu)化變量

之所以選擇0.04s是因為它可以以每秒25幀的速度進行1：1播放。是的，實際上我確實更改了仿真時間步長，因為25 fps看起來不錯。

為了找到時間步長，我手動增加了時間步長，直到找到可行的解決方案為止。有多種方法可以讓求解器自行發(fā)現(xiàn)最短的時間軌跡（主要是：讓它確定點之間的時間步長）。

成本函數(shù)

設(shè)置成本函數(shù)

所有成本都是平方和-> cost [0]2+ cost [1]2+ cost [2]2…依此類推。

最小化推力輸出——理想情況下，您希望在著陸時使用少量燃油。

最小化TVC的萬向節(jié)角度——移動噴嘴很費力，理想情況下，您希望它名義上指向下方。

最小化角速度——似乎有點荒唐，但我有一種直覺，即角速度/加速度會在發(fā)動機上施加最大的應(yīng)變，因此您希望將其保持在盡可能低的水平。

約束集1：初始條件和最終條件

初始條件是在空氣中以90m / s的速度向下旋轉(zhuǎn)90度然后開始向下飛行1000m。

初始條件和最終條件約束

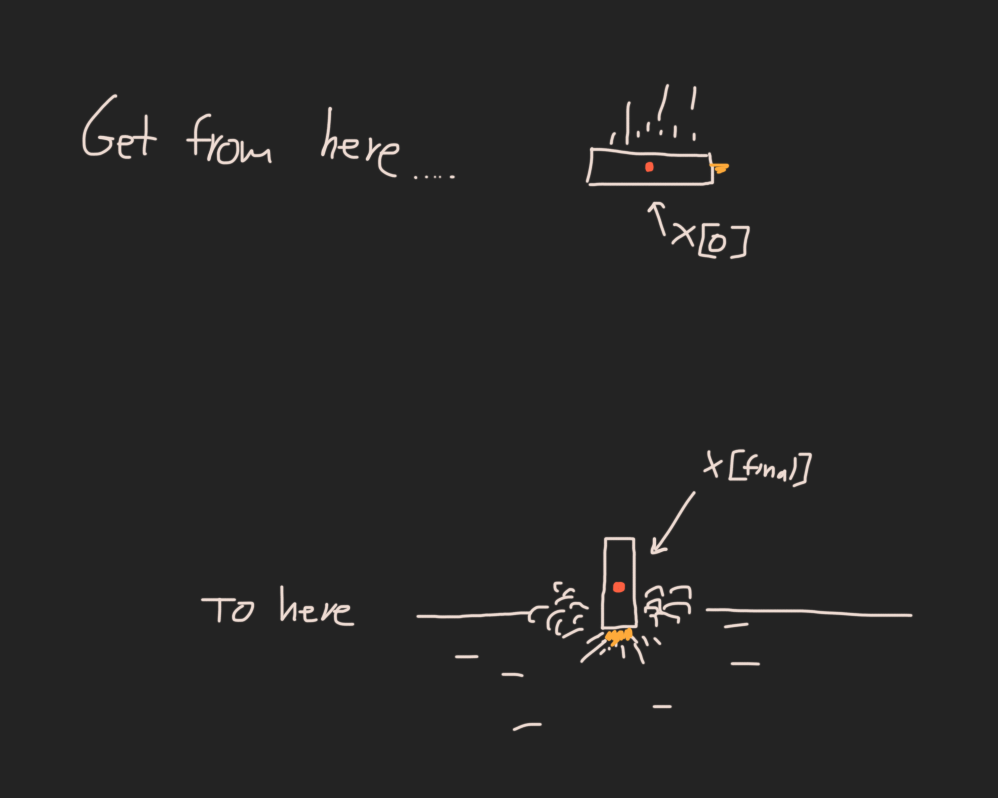
起始高度和速度來自飛行俱樂部的SN9數(shù)據(jù)：https：//flightclub.io/result/2d？code = SN91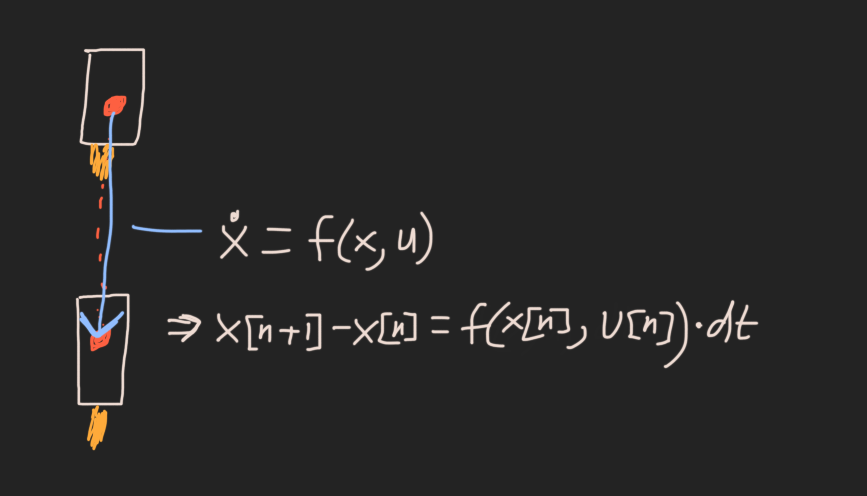

約束集2：動態(tài)

每個狀態(tài)時間步都必須服從：x [n + 1] -x [n] = f（x [n]，u [n]）* dt

本質(zhì)上，這是“不要破壞物理”的約束。它等效于火箭的離散時間模擬，下一個狀態(tài)等于當(dāng)前狀態(tài)+導(dǎo)數(shù)* dt。（注意：我在代碼中使用x_dot（）而不是f（），因為我認為它更易于閱讀）。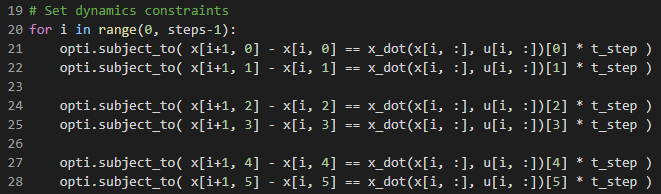

為狀態(tài)向量中的所有元素設(shè)置動力學(xué)約束

飛行常數(shù)和動力學(xué)功能：

g = 9.8
m = 100000公斤（猜測濕重和干重之間的一個很好的舍入數(shù)。實際上，當(dāng)您使用燃料時，這種情況會發(fā)生變化，但出于準確性考慮，我只是為了簡單起見）
長度= 50米
I =（1/12）* m *長度2（均勻桿的慣性）

定義f（x，u）= x_dot

（注意：這是一個相當(dāng)差的離散化，并且存在更好的方法，例如并置。但是，這是寫出來的最簡單，最快的方法）

約束集3：可變范圍

推力不能超過一個猛禽戰(zhàn)機的最大值，油門不能低于40％，推力矢量控制在每個方向上的擺角都不能超過20度 Raptor max取自維基百科，+-20度完全是個猜測，我很想知道是否有更可靠的數(shù)據(jù)用于此。

設(shè)置u的有界約束

優(yōu)化！

剩下要做的就是運行它！

選擇求解器并運行！

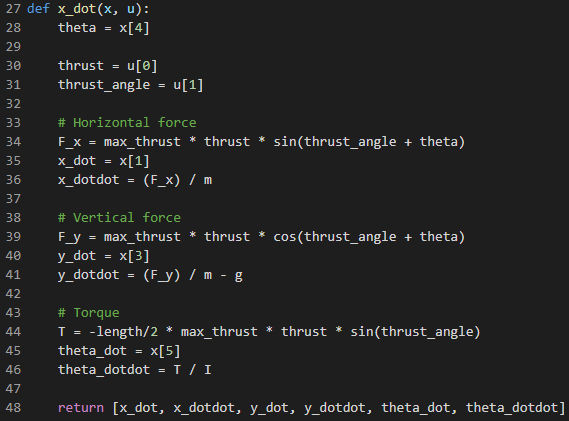
基本上就是這樣，您調(diào)用opti.solve（），然后將其轉(zhuǎn)換為Ipopt（開放源代碼優(yōu)化求解器）可以理解的問題。希望此消息應(yīng)該到達大量迭代打印的底部：

這就是我們想要看到的

狀態(tài)和控制陣列圖

下一部分代碼使用matplotlib制作了漂亮的動畫，需要花一點時間來生成所有幀，但結(jié)果還是很不錯的。

總結(jié)

雖然接近完美的軌道可能主要是讓我對事物的估計感到幸運，但仍有一些有趣的東西可以借鑒，主要是：

Starship很有可能要么遵循預(yù)先計劃的優(yōu)化軌跡，要么運行實時優(yōu)化以動態(tài)生成最優(yōu)軌跡。（或兩者混合）

不僅如此，我們可以進一步猜測它們的優(yōu)化成本函數(shù)/“目標”與我們的非常相似：最小化推力，最小化TVC角和最小化角速度。這條賽道有時幾乎是不可思議的，尤其是在雙向滑行的情況下。（我一直以為這是過沖，但這可能只是到達著陸點的最佳路徑）。這也是一個有趣的分析工具，我真的很想找出導(dǎo)致SN8和SN9著陸失敗的一些其他約束（需要進行一些調(diào)整：最終狀態(tài)不再是嚴格的約束）。

為什么實際上著陸火箭比這要難得多

“哇，我剛剛想出了SpaceX是如何著陸他們的火箭的！！”，但可悲的是，事實并非如此。

一旦生成了一條物理上可能的軌跡，該軌跡將您帶到了您想去的地方，那么您需要做的很多事情才能真正沿著該軌跡運動：狀態(tài)估計，閉環(huán)反饋控制，基于實際運動軌跡的動態(tài)更新時間條件……還有很多真正的航空工程師知道的東西。除此之外，這些求解器還需要花費很長時間才能運行，并且在線（實時）優(yōu)化很難正確而安全地完成：一個錯誤的輸入，您的求解器可能會發(fā)出“失敗”的聲音，從而導(dǎo)致故障發(fā)生。

下面是Lars Blackmore網(wǎng)站的鏈接，他是Starship EDL的首席工程師以及研究Falcon 9著陸技術(shù)的人。他的論文和其他出版物對如何在EDL問題中使用最佳控制進行了更為全面的概述。

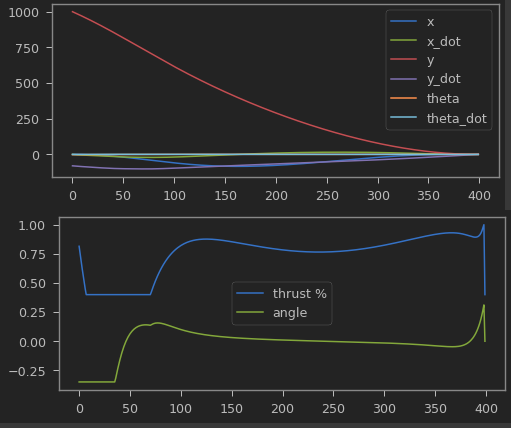
http://larsblackmore.com/

點擊下方閱讀原文加入社區(qū)會員

用 Python 解釋 SpaceX 如何進行火箭回收