引言

本著“凡我不能創(chuàng)造的，我就不能理解”的思想，本系列文章會基于純Python以及NumPy從零創(chuàng)建自己的深度學習框架，該框架類似PyTorch能實現(xiàn)自動求導。

要深入理解深度學習，從零開始創(chuàng)建的經驗非常重要，從自己可以理解的角度出發(fā)，盡量不適用外部完備的框架前提下，實現(xiàn)我們想要的模型。本系列文章的宗旨就是通過這樣的過程，讓大家切實掌握深度學習底層實現(xiàn)，而不是僅做一個調包俠。

上篇文章中，我們了解了線性回歸。本文就來通過metagrad實現(xiàn)線性回歸。

實現(xiàn)模型基類

class?Module:
????'''
????所有模型的基類
????'''

????def?parameters(self)?->?List[Parameter]:
????????parameters?=?[]
????????for?name,?value?in?inspect.getmembers(self):
????????????if?isinstance(value,?Parameter):
????????????????parameters.append(value)
????????????elif?isinstance(value,?Module):
????????????????parameters.extend(value.parameters())

????????return?parameters

????def?zero_grad(self):
????????for?p?in?self.parameters():
????????????p.zero_grad()

????def?__call__(self,?*args,?**kwargs):
????????return?self.forward(*args,?**kwargs)

????def?forward(self,?*args,?**kwargs)?->?Tensor:
????????raise?NotImplementedError

類似PyTorch，我們也實現(xiàn)一個模型的基類，其中存放一些通用方法。代碼如上。主要實現(xiàn)了梯度清零方法。

其中Parameter的定義如下：

class?Parameter(Tensor):
????def?__init__(self,?data:?Union[Arrayable,?Tensor])?->?None:
????????
????????if?isinstance(data,?Tensor):
????????????data?=?data.data
????????#?Parameter都是需要計算梯度的
????????super().__init__(data,?requires_grad=True)

Parameter默認需要計算梯度，在Module的parameters()方法中利用Parameter類獲取模型的所有參數(shù)。

實現(xiàn)線性回歸

class?Linear(Module):
????r"""
?????????對給定的輸入進行線性變換:?:math:`y=xA^T?+?b`

????????Args:
????????????in_features:?每個輸入樣本的大小
????????????out_features:?每個輸出樣本的大小
????????????bias:?是否含有偏置，默認?``True``
????????Shape:
????????????-?Input:?`(*,?H_in)`?其中?`*`?表示任意維度，包括none,這里?`H_{in}?=?in_features`
????????????-?Output:?:math:`(*,?H_out)`?除了最后一個維度外，所有維度的形狀都與輸入相同，這里H_out?=?out_features`
????????Attributes:
????????????weight:?可學習的權重，形狀為?`(out_features,?in_features)`.
????????????bias:???可學習的偏置，形狀?`(out_features)`.
????????"""

????def?__init__(self,?in_features:?int,?out_features:?int,?bias:?bool?=?True)?->?None:
????????self.in_features?=?in_features
????????self.out_features?=?out_features

????????self.weight?=?Parameter(Tensor.empty((out_features,?in_features)))
????????if?bias:
????????????self.bias?=?Parameter(Tensor.zeros(out_features))
????????else:
????????????self.bias?=?None
????????self.reset_parameters()

????def?reset_parameters(self)?->?None:
????????self.weight.assign(np.random.randn(self.out_features,?self.in_features))

????def?forward(self,?input:?Tensor)?->?Tensor:
????????x?=?input?@?self.weight.T
????????if?self.bias?is?not?None:
????????????x?=?x?+?self.bias

????????return?x

讓我們的線性回歸模型繼承Module，同時定義權重和偏置大小。最后我們只需要實現(xiàn)前向傳播算法，反向傳播就交給我們的自動求導機制去完成。

這樣，我們的線性回歸模型就實現(xiàn)完成了。但為了我們的模型能夠學習，我們需要定義損失函數(shù)。

實現(xiàn)損失基類

class?_Loss(Module):
????'''
????損失的基類
????'''
????reduction:?str??#?none?|?mean?|?sum

????def?__init__(self,?reduction:?str?=?"mean")?->?None:
????????self.reduction?=?reduction

參考了PyTorch，聚合方法支持均值和求和。

實現(xiàn)均方誤差

class?MSELoss(_Loss):
????def?__init__(self,?reduction:?str?=?"mean")?->?None:
????????'''
????????均方誤差
????????'''
????????super().__init__(reduction)

????def?forward(self,?input:?Tensor,?target:?Tensor)?->?Tensor:
????????assert?input.size?==?target.size,?f"Using?a?target?size?({target.size})?that?is?different?to?the?input?size?"?\
???????????????????????????????????????????f"({input.size}).?This?will?likely?lead?to?incorrect?results?due?to?"?\
???????????????????????????????????????????f"broadcasting.?Please?ensure?they?have?the?same?size."

????????errors?=?(input?-?target)?**?2
????????if?self.reduction?==?"mean":
????????????loss?=?errors.sum(keepdims=False)?/?len(input)
????????elif?self.reduction?==?"sum":
????????????loss?=?errors.sum(keepdims=False)
????????else:
????????????loss?=?errors

????????return?loss

這里的input其實是模型的輸出，target真實輸出。

有了損失函數(shù)后，我們還需要優(yōu)化方法來進行參數(shù)優(yōu)化。

實現(xiàn)優(yōu)化方法

class?Optimizer:
????def?__init__(self,?params:?List[Parameter])?->?None:
????????self.params?=?params

????def?zero_grad(self)?->?None:
????????for?p?in?self.params:
????????????p.zero_grad()

????def?step(self)?->?None:
????????raise?NotImplementedError

我們如上實現(xiàn)了優(yōu)化方法的基類。下面就是實現(xiàn)隨機梯度下降法(SGD)。

實現(xiàn)隨機梯度下降法

class?SGD(Optimizer):
????'''
????隨機梯度下降
????'''

????def?__init__(self,?params:?List[Parameter],?lr:?float?=?1e-3)?->?None:
????????super().__init__(params)
????????self.lr?=?lr

????def?step(self)?->?None:
????????for?p?in?self.params:
????????????p?-=?p.grad?*?self.lr

lr是學習率，每次調用step()都會進行參數(shù)更新。

線性回歸實例

我們基于上篇文章中采集的深圳市南山區(qū)臨近地鐵口二手房價的數(shù)據(jù)為例：

#?面積
areas?=?[64.4,?68,?74.1,?74.,?76.9,?78.1,?78.6]
#?掛牌售價
prices?=?[6.1,?6.25,?7.8,?6.66,?7.82,?7.14,?8.02]

我們先考慮面積和掛牌價(可能是指導價 ?單位：萬/㎡)之間的關系。

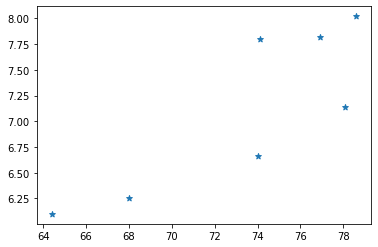
看上去似乎有一定的線性關系。我們這里簡單的考慮套內面積，實際上我們買房時還會考慮房齡、離地鐵口距離、小區(qū)周邊環(huán)境、空氣質量、小區(qū)綠化區(qū)面積等。

這里我們嘗試通過畫一條直線，使得該直線盡可能和每個樣本的距離最短。

#?!pip?install?git+https://github.com/nlp-greyfoss/metagrad.git?--upgrade
from?metagrad.loss?import?MSELoss
from?metagrad.module?import?Linear
from?metagrad.optim?import?SGD
from?metagrad.tensor?import?Tensor

model?=?Linear(1,?1)

optimizer?=?SGD(model.parameters(),?lr=1e-1)

loss?=?MSELoss()

#?面積
areas?=?[64.4,?68,?74.1,?74.,?76.9,?78.1,?78.6]
#?掛牌售價
prices?=?[6.1,?6.25,?7.8,?6.66,?7.82,?7.14,?8.02]

X?=?Tensor(areas).reshape((-1,?1))
y?=?Tensor(prices).reshape((-1,?1))

epochs?=?100
losses?=?[]
for?epoch?in?range(epochs):
??l?=?loss(model(X),?y)
??optimizer.zero_grad()
??l.backward()
??optimizer.step()
??epoch_loss?=?l.data
??
??losses.append(epoch_loss)

??print(f'epoch?{epoch?+?1},?loss?{float(epoch_loss):f}')

上面就是通過我們自己的metagrad實現(xiàn)的線性回歸學習過程，是不是看上去有那味了。

輸出：

epoch?1,?loss?198.071304
epoch?2,?loss?232059248.000000
epoch?3,?loss?272126879727616.000000
epoch?4,?loss?319112649512125988864.000000
epoch?5,?loss?374211056107641585692311552.000000
epoch?6,?loss?438822818730812850430760481456128.000000
epoch?7,?loss?inf
...

怎么損失不降反增了!?

莫慌，我們只有一個變量，不存在兩個變量的量綱不同的問題。此時，該顯示一下我們AI調參師的技術了。

損失太大，可能是梯度太大了，我們直接將學習率調小。

optimizer?=?SGD(model.parameters(),?lr=1e-4)

我們修改學習率為1e-4：

epoch?1,?loss?21798.214844
epoch?2,?loss?153.602646
epoch?3,?loss?1.260477
epoch?4,?loss?0.188241
epoch?5,?loss?0.180694
epoch?6,?loss?0.180641
epoch?7,?loss?0.180641
epoch?8,?loss?0.180641
epoch?9,?loss?0.180641
epoch?10,?loss?0.180641
epoch?11,?loss?0.180641
epoch?12,?loss?0.180640
...
epoch?99,?loss?0.180638
epoch?100,?loss?0.180638

從輸出可以看出，第4次迭代后，損失就一直不變了，我們看一下學習率曲線：

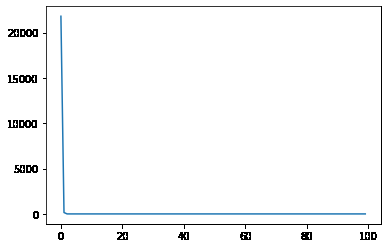
我們可以打印出得到的參數(shù)：

>?w,?b?=?model.weight.data.item(),model.bias.data.item()
>?print(f'w:?{w},?b:{b}')
w:?0.09660441144108287,?b:0.026999891111711846

然后畫出線性回歸擬合的直線：

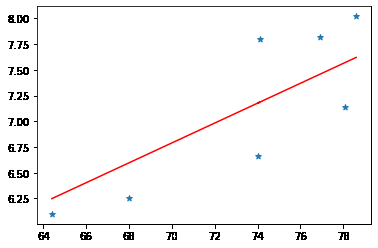
看上去還可以，如果你要買房的話，建議你買直線下面的房子。

基于我們這點訓練樣本，得到最后的損失為，我們能否使它再次降低呢？

一種方法是收集更多的數(shù)據(jù)，另一種方法是利用所有的維度。我們還有一個房齡維度沒有利用。下面把它加進來。

#?面積
>?areas?=?[64.4,?68,?74.1,?74.,?76.9,?78.1,?78.6]
#?房齡
>?ages?=?[31,?21,?19,?24,?17,?16,?17]
>?X?=?np.stack([areas,?ages]).T
>?print(X)
array([[64.4,?31.?],
???????[68.?,?21.?],
???????[74.1,?19.?],
???????[74.?,?24.?],
???????[76.9,?17.?],
???????[78.1,?16.?],
???????[78.6,?17.?]])

第1列是面積，第2列是房齡，每行數(shù)據(jù)代表一個樣本。

下面我們改寫上面的線性回歸代碼，再次訓練一個線性回歸模型：

model?=?Linear(2,?1)?#?in_features:?2??out_features:?1

optimizer?=?SGD(model.parameters(),?lr=1e-4)

loss?=?MSELoss()

#?面積
areas?=?[64.4,?68,?74.1,?74.,?76.9,?78.1,?78.6]
#?房齡
ages?=?[31,?21,?19,?24,?17,?16,?17]

X?=?np.stack([areas,?ages]).T
#?掛牌售價
prices?=?[6.1,?6.25,?7.8,?6.66,?7.82,?7.14,?8.02]


X?=?Tensor(X)
y?=?Tensor(prices).reshape((-1,?1))

epochs?=?1000
losses?=?[]
for?epoch?in?range(epochs):
??l?=?loss(model(X),?y)
??optimizer.zero_grad()
??l.backward()
??optimizer.step()
??epoch_loss?=?l.data

??losses.append(epoch_loss)
??if?(epoch+1)?%?20?==?0:
????print(f'epoch?{epoch?+?1},?loss?{float(epoch_loss):f}')

輸出:

epoch?20,?loss?10.742877
epoch?40,?loss?8.136241
epoch?60,?loss?6.171517
epoch?80,?loss?4.690628
epoch?100,?loss?3.574423
epoch?120,?loss?2.733095
epoch?140,?loss?2.098954
epoch?160,?loss?1.620976
epoch?180,?loss?1.260706
epoch?200,?loss?0.989156
epoch?220,?loss?0.784478
epoch?240,?loss?0.630204
epoch?260,?loss?0.513921
epoch?280,?loss?0.426275
...
epoch?1000,?loss?0.158022

加上房齡信息，最終可以使損失下降到。我們來看一下此時的權重和偏置：

>?w,?b?=?model.weight.data,model.bias.data.item()
>?print(f'w:?{w},?b:{b}')
w:?[[?0.10354146?-0.02362296]],?b:-0.00232952055510911

可以看到，房齡特征對應的權重為，所以說房齡越大，房子的價值就越小，這一關系還是學到了的。

我們的訓練集才7個樣本，這真的是太少了，如果你收集更多的數(shù)據(jù)，一定可以獲得更好的效果。

總結

本文我們通過metagrad實現(xiàn)了線性回歸，以及一些基類方法。下篇文章我們就來學習邏輯回歸。