動(dòng)畫 | 什么是紅黑樹?(與2-3-4樹等價(jià))
來源：算法無遺策
作者：我脫下短袖
二分搜索樹是為了快速查找而生，它是一顆二叉樹，每一個(gè)節(jié)點(diǎn)只有一個(gè)元素（值或鍵值對(duì)），左子樹所有節(jié)點(diǎn)的值均小于父節(jié)點(diǎn)的值，右子樹所有的值均大于父節(jié)點(diǎn)的值，左右子樹也是一顆二分搜索樹，而且沒有鍵值相等的節(jié)點(diǎn)。它的查找、插入和刪除的時(shí)間復(fù)雜度都與樹高成比例，期望值是O(logn)。
但是插入數(shù)組如[15，17，13，12，9，7]，二分搜索樹就暴露了缺點(diǎn)，將樹退化成線性表，查找的時(shí)間復(fù)雜度達(dá)到最壞時(shí)間復(fù)雜度O(n)。?動(dòng)畫：二分搜索樹退化成線性表?
那有沒有插入和刪除操作都能保持樹的完美平衡性（任何一個(gè)節(jié)點(diǎn)到其葉子節(jié)點(diǎn)的路徑長度都是相等的）？?有，B樹。B樹是一種自平衡的樹，根節(jié)點(diǎn)到其葉子節(jié)點(diǎn)的路徑高度都是一樣的，能夠保持?jǐn)?shù)據(jù)有序（通過中序遍歷能得到有序數(shù)據(jù)）。B樹一個(gè)節(jié)點(diǎn)可以擁有2個(gè)以上的子樹，如2-3樹、2-3-4樹甚至2-3-4-5-6-7-8樹，它們滿足二分搜索樹的性質(zhì)，但它們不屬于二叉樹，也不屬于二分搜索樹。?2-3-4樹的完美平衡，每條從根節(jié)點(diǎn)到葉子節(jié)點(diǎn)的路徑的高度都是一樣的?2-3-4樹有以下節(jié)點(diǎn)組成：?2-節(jié)點(diǎn)，含有一個(gè)元素（值或鍵值對(duì)）和兩個(gè)子樹（左右子樹），左子樹所有的值均小于父節(jié)點(diǎn)的值，右子樹所有的值均大于父節(jié)點(diǎn)的值；?3-節(jié)點(diǎn)，含有兩個(gè)元素和三個(gè)子樹，左子樹所有的值均小于父節(jié)點(diǎn)最小元素的值，中間子樹所有的值均位于父節(jié)點(diǎn)兩個(gè)元素之間，右子樹所有的值均大于父節(jié)點(diǎn)最大元素的值；?4-節(jié)點(diǎn)，含有三個(gè)元素和四個(gè)子樹，節(jié)點(diǎn)之間的比較也滿足二分搜索樹的性質(zhì)。?2-3-4樹查找算法?2-3-4樹的查找類似二分搜索樹的查找。?2-3-4樹插入算法?2-3-4樹的插入算法是消除當(dāng)前節(jié)點(diǎn)是4-節(jié)點(diǎn)，將4-節(jié)點(diǎn)分解成多個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并成3-節(jié)點(diǎn)或4-節(jié)點(diǎn)。?沿著鏈接向下進(jìn)行變換分解4-節(jié)點(diǎn)分為兩種情況：?1）4-節(jié)點(diǎn)作為根節(jié)點(diǎn)，分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)作為根節(jié)點(diǎn)；?2）當(dāng)前節(jié)點(diǎn)為4-節(jié)點(diǎn)，分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并成3-節(jié)點(diǎn)或4-節(jié)點(diǎn)；?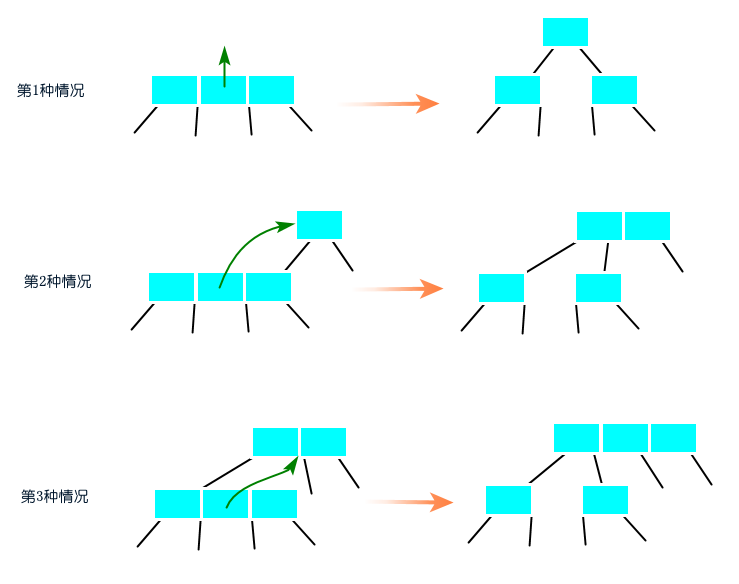
圖：沿著鏈接向下進(jìn)行變換，分解4-節(jié)點(diǎn)?在沿著左右鏈接向下進(jìn)行變換的同時(shí)，也會(huì)進(jìn)行命中查找。如果元素是鍵值對(duì)的話，查找命中將舊的值賦值為新的值；如果元素是一個(gè)值的話，查找命中將忽略之，因?yàn)槎炙阉鳂湫枰獫M足沒有相等的元素；如果需要支持重復(fù)的元素，則在元素對(duì)象添加count屬性，默認(rèn)為1。?如果查找未命中，則將待插入元素插入在葉子節(jié)點(diǎn)上。樹底下插入一個(gè)元素只有兩種情況：向2-節(jié)點(diǎn)中插入和向3-節(jié)點(diǎn)中插入。?
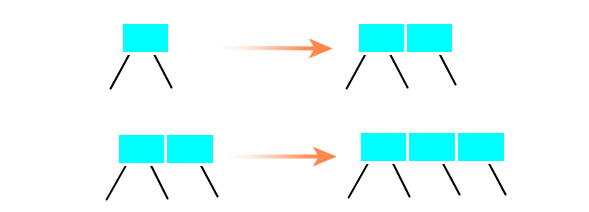圖：樹底下插入一個(gè)元素?2-3-4樹刪除算法?2-3-4樹的刪除算法是消除當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，向兄弟節(jié)點(diǎn)或父節(jié)點(diǎn)借一個(gè)元素過來。?刪除最小元素?從根節(jié)點(diǎn)的左孩子開始，沿著左鏈接向下進(jìn)行變換可以分為三種情況：?1）當(dāng)前節(jié)點(diǎn)不是2-節(jié)點(diǎn)，跳過；?2）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，將當(dāng)前節(jié)點(diǎn)、父節(jié)點(diǎn)最小元素和兄弟節(jié)點(diǎn)合并為4-節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成4-節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，將兄弟節(jié)點(diǎn)的最小元素移到父節(jié)點(diǎn)，父節(jié)點(diǎn)的最小元素移到當(dāng)前節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成3-節(jié)點(diǎn)。?
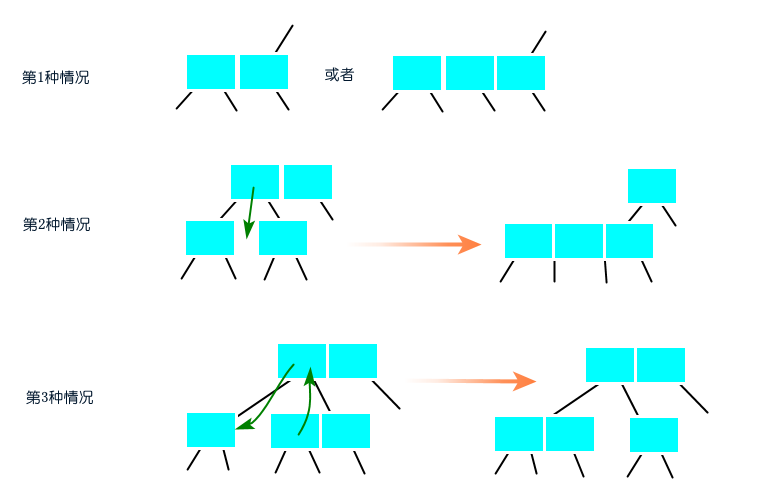圖：沿著左鏈接向下進(jìn)行變換?刪除最大元素?從根節(jié)點(diǎn)的右孩子開始，沿著右鏈接向下進(jìn)行變換也同樣分為三種情況：?1）當(dāng)前節(jié)點(diǎn)不是2-節(jié)點(diǎn)，跳過；?2）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，將當(dāng)前節(jié)點(diǎn)、父節(jié)點(diǎn)的最大元素和兄弟節(jié)點(diǎn)合并為4-節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成4-節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，將兄弟節(jié)點(diǎn)的最大元素移到父節(jié)點(diǎn)，父節(jié)點(diǎn)的最大元素移到當(dāng)前節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成3-節(jié)點(diǎn)。?
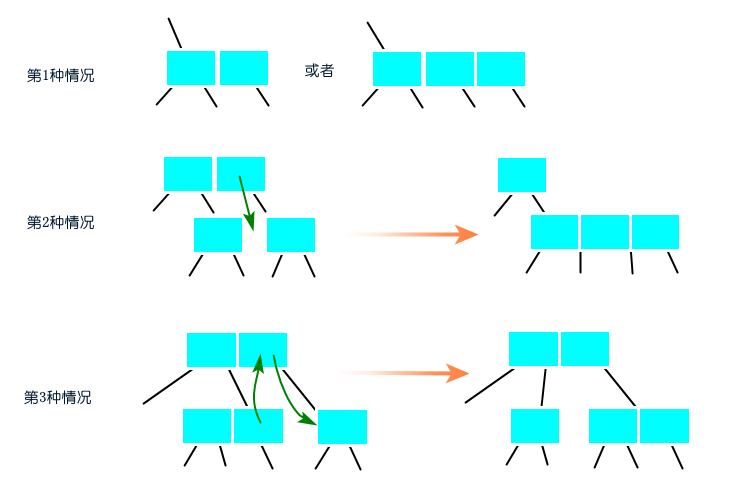圖：沿著右鏈接向下進(jìn)行變換?刪除任意元素?學(xué)習(xí)過刪除最小元素和刪除最大元素算法之后，刪除任意元素的算法自然就簡單了。刪除任意元素算法需要先進(jìn)行命中查找，若查找命中，則將右子樹的最小值替換掉待刪除元素，然后將右子樹進(jìn)行刪除最小元素的算法。?2-3-4樹雖滿足二分搜索樹的性質(zhì)，但不是一顆二分搜索樹。如果期望它是一顆二分搜索樹，就需要將3-節(jié)點(diǎn)和4-節(jié)點(diǎn)替換為多個(gè)2-節(jié)點(diǎn)，還需要注明元素之間的關(guān)系（用紅鏈接表示）。?替換3-節(jié)點(diǎn)和4-節(jié)點(diǎn)?
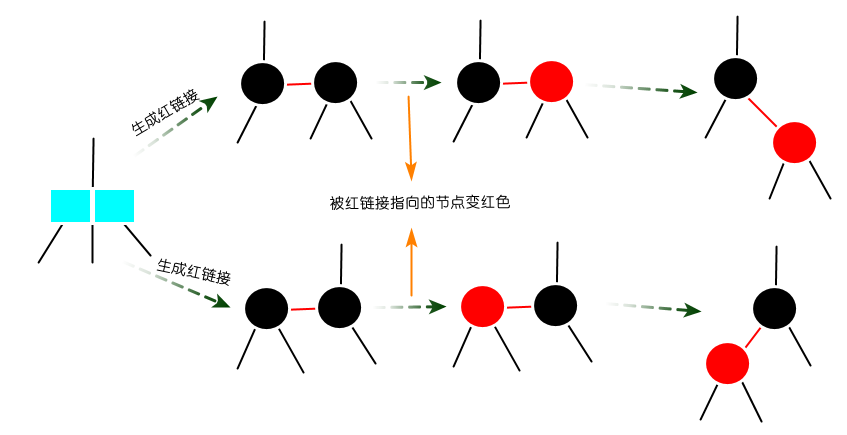圖：替換3-節(jié)點(diǎn)?
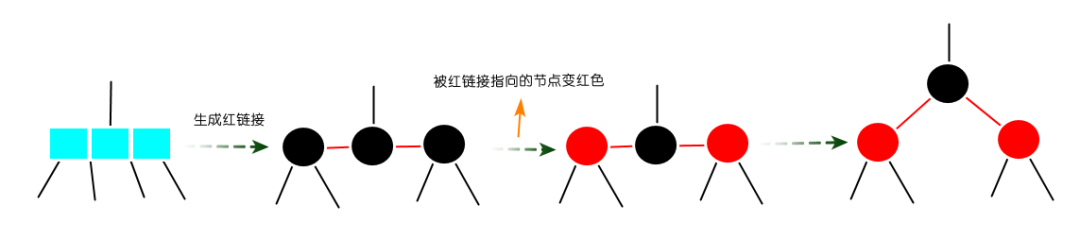圖：替換4-節(jié)點(diǎn)?但是存在一個(gè)問題，2-3-4樹因?yàn)?-節(jié)點(diǎn)的不同表示會(huì)有很多種不同的紅黑樹，3-節(jié)點(diǎn)既可以左傾，也可以右傾。所以為了保證樹的唯一性，3-節(jié)點(diǎn)只考慮左傾，當(dāng)然你也可以只考慮右傾。?這樣對(duì)于任何一顆2-3-4樹，只考慮左傾的情況下，都能得到唯一的一顆對(duì)應(yīng)的紅黑樹，這種樹也叫左傾紅黑樹，相對(duì)比較減少了復(fù)雜性，設(shè)計(jì)更容易被實(shí)現(xiàn)。?紅黑樹查找算法?紅黑樹的查找算法和二分搜索樹一樣。?關(guān)于鏈接的顏色變換只跟顏色轉(zhuǎn)換有關(guān)，而旋轉(zhuǎn)不會(huì)改變鏈接的顏色變換，只在被紅鏈接指向的節(jié)點(diǎn)變成紅色，被黑鏈接指向的節(jié)點(diǎn)變成黑色。?旋轉(zhuǎn)?旋轉(zhuǎn)是將不滿足紅黑樹性質(zhì)的3-節(jié)點(diǎn)和4-節(jié)點(diǎn)進(jìn)行旋轉(zhuǎn)，如果3-節(jié)點(diǎn)出現(xiàn)右鏈接，則將右鏈接通過左旋轉(zhuǎn)變成左鏈接；如果4-節(jié)點(diǎn)出現(xiàn)一個(gè)紅節(jié)點(diǎn)連著兩條紅鏈接，則將4-節(jié)點(diǎn)配平。?左旋轉(zhuǎn)?
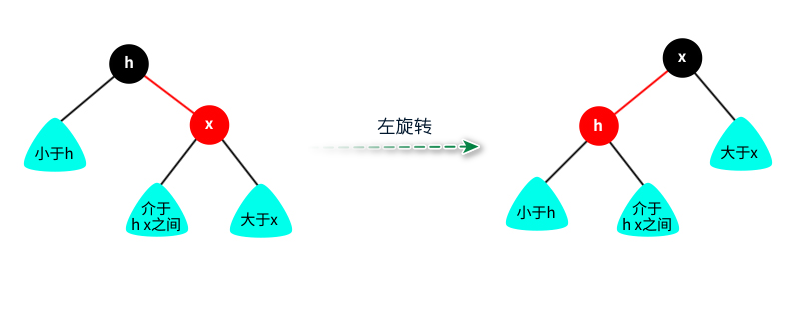圖：左旋轉(zhuǎn)?右旋轉(zhuǎn)?
圖：右旋轉(zhuǎn)?
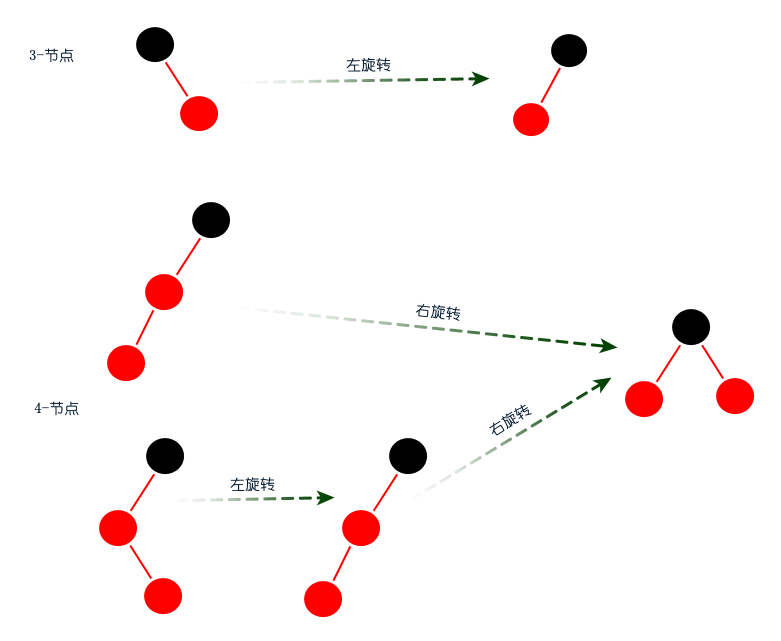圖：3-節(jié)點(diǎn)和4-節(jié)點(diǎn)的旋轉(zhuǎn)?Code：右旋轉(zhuǎn)和左旋轉(zhuǎn)?
?顏色轉(zhuǎn)換?顏色轉(zhuǎn)換只應(yīng)用于4-節(jié)點(diǎn)。?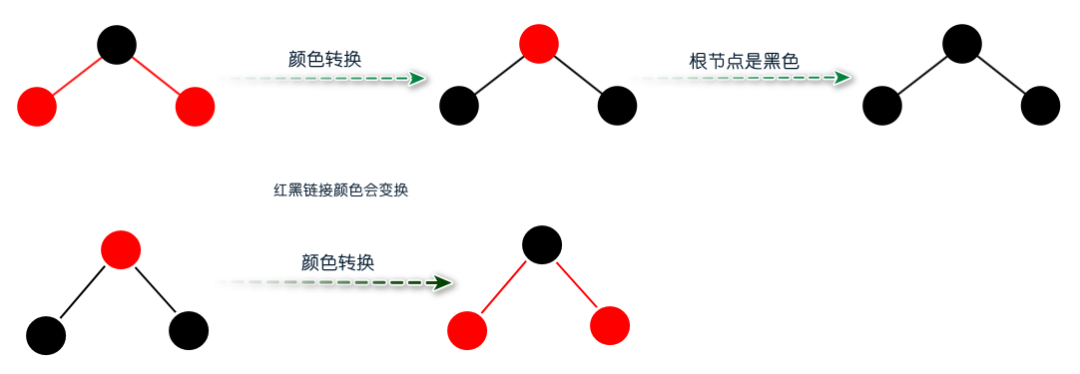
圖：顏色轉(zhuǎn)換?Code：顏色轉(zhuǎn)換?
?紅黑樹插入算法?回顧之前的2-3-4樹的插入算法，它有兩個(gè)過程：沿著鏈接向下進(jìn)行分解4-節(jié)點(diǎn)和樹底下插入一個(gè)元素。?紅黑樹的插入算法和2-3-4樹的插入算法類似，它不僅包含前面兩個(gè)過程，還增加了向上進(jìn)行變換的過程，此過程是將3-節(jié)點(diǎn)左傾和4-節(jié)點(diǎn)配平。?紅黑樹插入算法會(huì)先從根節(jié)點(diǎn)開始，沿著左右鏈接向下進(jìn)行變換，目的是為了分解4-節(jié)點(diǎn)。如果該節(jié)點(diǎn)的左右孩子都是紅節(jié)點(diǎn)，則通過flipColors方法進(jìn)行顏色轉(zhuǎn)換，接著進(jìn)行下一個(gè)子節(jié)點(diǎn)；如果不是，則直接進(jìn)行下一個(gè)子節(jié)點(diǎn)。?到達(dá)樹底的時(shí)候，則意味著可以開始插入新的元素。?如果紅黑樹目前是一顆空樹，插入紅色的元素作為第一個(gè)節(jié)點(diǎn)，然后該節(jié)點(diǎn)變成黑色。如果不是一顆空樹，插入元素分為三種情況：向2-節(jié)點(diǎn)插入新元素、向3-節(jié)點(diǎn)插入新元素和向4-節(jié)點(diǎn)插入新元素。?向2-節(jié)點(diǎn)插入新元素?向2-節(jié)點(diǎn)插入新元素很簡單，如果新元素的值小于父節(jié)點(diǎn)，直接插入紅色的節(jié)點(diǎn)即可；如果新元素的值大于父節(jié)點(diǎn)，則產(chǎn)生一個(gè)紅色右鏈接，插完之后則將3-節(jié)點(diǎn)進(jìn)行左旋轉(zhuǎn)，將右鏈接變成左鏈接，被紅鏈接指向的節(jié)點(diǎn)變成紅色，被黑鏈接指向的節(jié)點(diǎn)變成黑色。?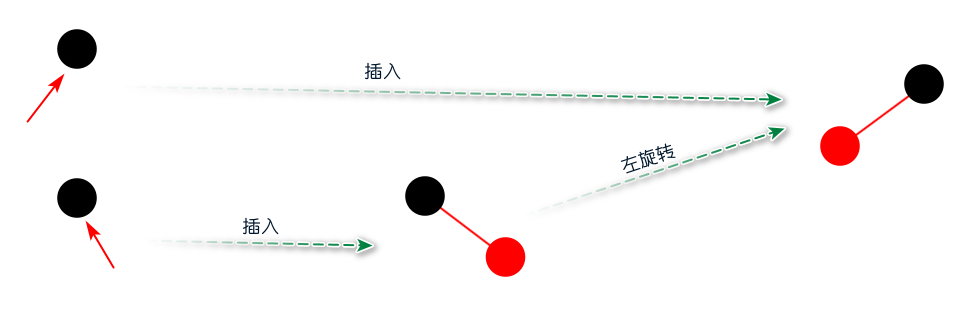
圖：向2-節(jié)點(diǎn)插入新元素?向3-節(jié)點(diǎn)插入新元素?因?yàn)榍懊娴?-節(jié)點(diǎn)進(jìn)行過旋轉(zhuǎn)，此時(shí)的3-節(jié)點(diǎn)肯定滿足左傾紅黑樹的性質(zhì)。向3-節(jié)點(diǎn)插入新元素分為三種情況：?1）新元素的值位于3-節(jié)點(diǎn)中的兩元素之間；?2）新元素的值小于3-節(jié)點(diǎn)中的最小元素；?3）新元素的值大于3-節(jié)點(diǎn)中的最大元素。?
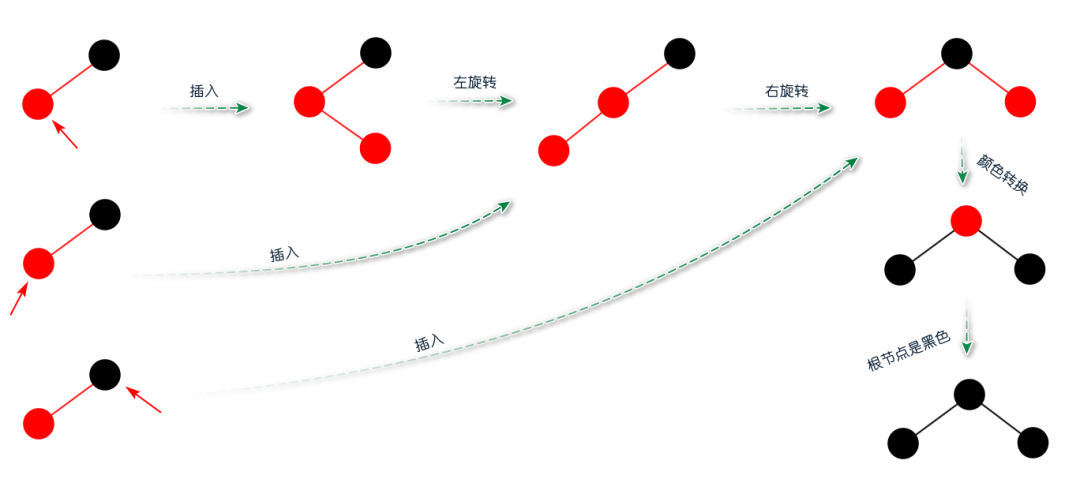圖：向3-節(jié)點(diǎn)插入新元素?向4-節(jié)點(diǎn)插入新元素?向4-節(jié)點(diǎn)插入新元素之前需要先進(jìn)行顏色轉(zhuǎn)換，才可以進(jìn)行插入新的元素。?
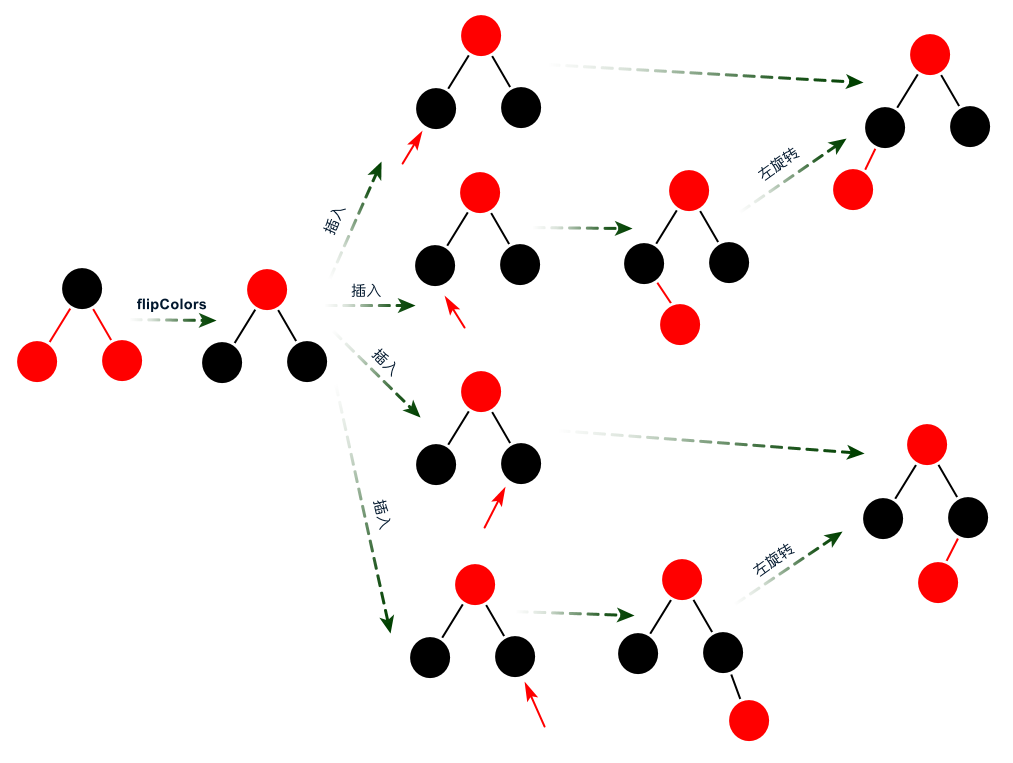圖：向4-節(jié)點(diǎn)插入新元素?插完新元素之后需要滿足紅黑樹的性質(zhì)，則在沿著父節(jié)點(diǎn)的鏈接向上進(jìn)行變換，具體做法和向3-節(jié)點(diǎn)插入新元素的做法類似，通過左旋轉(zhuǎn)將3-節(jié)點(diǎn)左傾和左右旋轉(zhuǎn)將4-節(jié)點(diǎn)配平，沒有顏色轉(zhuǎn)換。?動(dòng)畫：2-3-4樹與紅黑樹的插入?
Code：紅黑樹插入算法?
?紅黑樹刪除算法?紅黑樹刪除算法也需要進(jìn)行旋轉(zhuǎn)和顏色轉(zhuǎn)換操作，在插入算法中為了待插入元素所在的節(jié)點(diǎn)不是4-節(jié)點(diǎn)，所以在沿著左右鏈接向下進(jìn)行變換時(shí)將4-節(jié)點(diǎn)分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并；而在刪除算法中為了待刪除元素所在的節(jié)點(diǎn)不是2-節(jié)點(diǎn)，所以在沿著左右鏈接向下進(jìn)行變換時(shí)將2-節(jié)點(diǎn)向其它不是2-節(jié)點(diǎn)的節(jié)點(diǎn)（兄弟節(jié)點(diǎn)或父節(jié)點(diǎn)）借一個(gè)元素過來，合并成3-節(jié)點(diǎn)。?所以，只要是2-節(jié)點(diǎn)的節(jié)點(diǎn)，如果兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，就將兄弟節(jié)點(diǎn)的與父節(jié)點(diǎn)鄰近的元素移到父節(jié)點(diǎn)，而父節(jié)點(diǎn)將與當(dāng)前節(jié)點(diǎn)鄰近的元素移到當(dāng)前節(jié)點(diǎn)；如果兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，則將父節(jié)點(diǎn)的與當(dāng)前節(jié)點(diǎn)鄰近的元素移到當(dāng)前節(jié)點(diǎn)。（是不是很繞？待會(huì)在后面刪除最值算法中詳細(xì)給出）?然后刪除完一個(gè)元素之后需要進(jìn)行修復(fù)調(diào)整，將這個(gè)樹滿足紅黑樹的性質(zhì)。如果右鏈接是紅色，將右鏈接通過左旋轉(zhuǎn)變成左鏈接；如果有連續(xù)的左鏈接，通過右旋轉(zhuǎn)配平，然后進(jìn)行顏色轉(zhuǎn)換。?Code：向上變換（修復(fù)調(diào)整）?
?刪除最小元素?刪除最小元素算法和二分搜索樹一樣，一直遞歸它的左孩子，直到它的左孩子為空才進(jìn)行刪除這個(gè)最小元素。但是紅黑樹在遞歸的同時(shí)如何旋轉(zhuǎn)和顏色轉(zhuǎn)換是個(gè)問題。?刪除最小元素算法一直沿著左鏈接向下進(jìn)行轉(zhuǎn)換，對(duì)照2-3-4樹，我們可以給出三種情況，從根節(jié)點(diǎn)開始：?1）當(dāng)前節(jié)點(diǎn)（父節(jié)點(diǎn)位置）的左子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，直接進(jìn)行下一個(gè)節(jié)點(diǎn)（左子節(jié)點(diǎn)）；?2）當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)和右子節(jié)點(diǎn)都是2-節(jié)點(diǎn)，則將左子節(jié)點(diǎn)、當(dāng)前節(jié)點(diǎn)的最小元素和右子節(jié)點(diǎn)合并成4-節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)是2-節(jié)點(diǎn)，右子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，則將右子節(jié)點(diǎn)的最小元素移到當(dāng)前節(jié)點(diǎn)的位置，當(dāng)前節(jié)點(diǎn)的最小元素移到左子節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)。?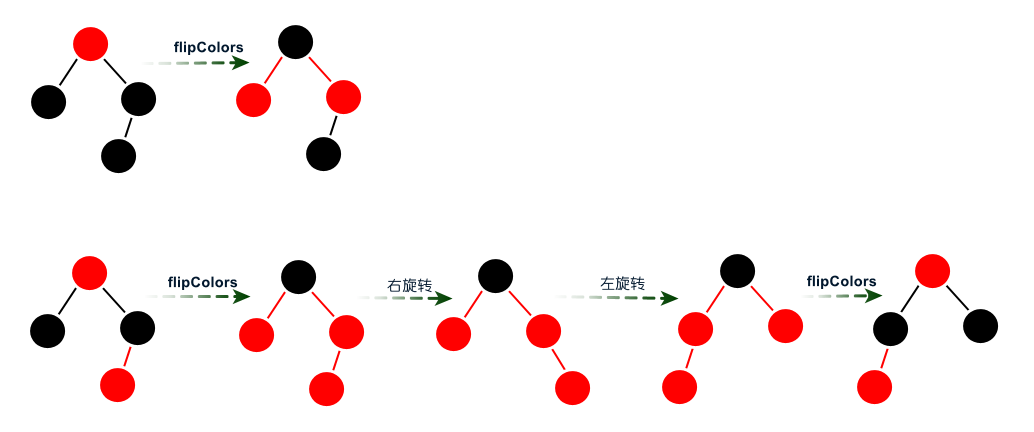
圖：沿著左鏈接向下進(jìn)行轉(zhuǎn)換?Code：沿著左鏈接向下變換?
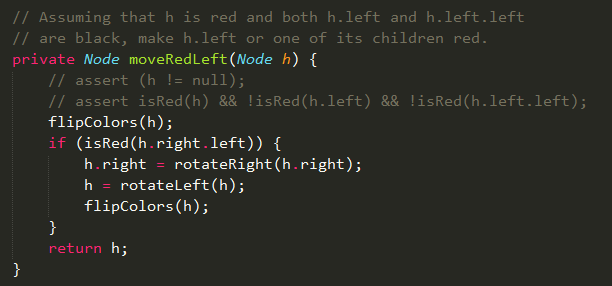?直到某元素左孩子為空的時(shí)候，此時(shí)的元素是這個(gè)樹的最小元素。因?yàn)橥ㄟ^前面的轉(zhuǎn)換，最小元素肯定被一個(gè)紅鏈接指向，刪除這個(gè)元素之后通過balance方法修復(fù)調(diào)整為紅黑樹。?Code：刪除最小元素算法?
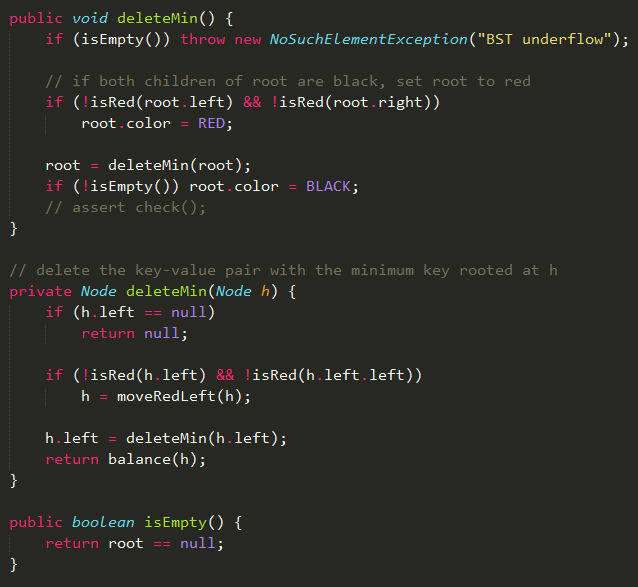?刪除最大元素?刪除最大元素算法和刪除最小元素算法類似的，也分為三種情況：?1）當(dāng)前節(jié)點(diǎn)（父節(jié)點(diǎn)位置）的右子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，直接進(jìn)行下一個(gè)節(jié)點(diǎn)（右子節(jié)點(diǎn)）；?2）當(dāng)前節(jié)點(diǎn)的右子節(jié)點(diǎn)和左子節(jié)點(diǎn)都是2-節(jié)點(diǎn)，則將右子節(jié)點(diǎn)、當(dāng)前節(jié)點(diǎn)的最大元素和左子節(jié)點(diǎn)合并成4-節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)的右子節(jié)點(diǎn)是2-節(jié)點(diǎn)，左子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，則將左子節(jié)點(diǎn)的最大元素移到當(dāng)前節(jié)點(diǎn)的位置，當(dāng)前節(jié)點(diǎn)的最大元素移到左子節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)。?
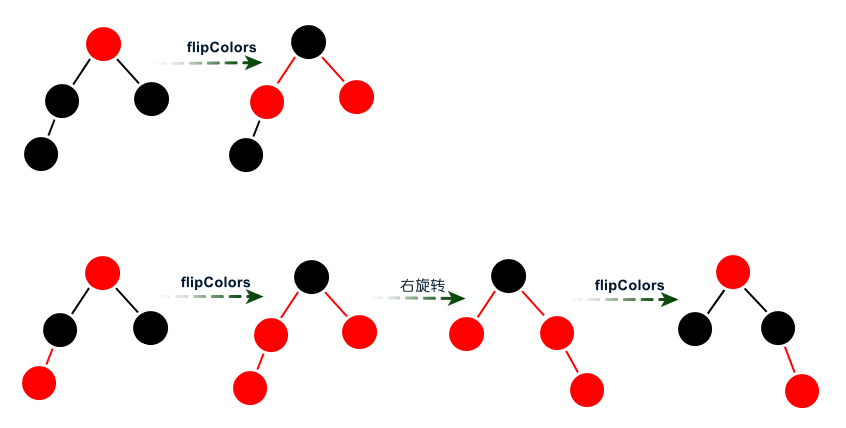圖：沿著右鏈接向下進(jìn)行變換?Code：沿著右鏈接向下變換?
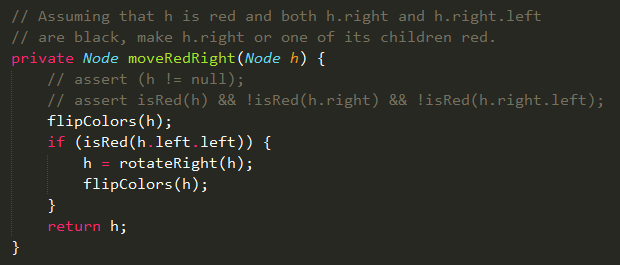?Code：刪除最大元素算法?
?刪除任意元素?學(xué)習(xí)過前面的刪除最小元素算法和刪除最大元素算法，刪除任意元素會(huì)變得很簡單。刪除最小元素算法會(huì)一直沿著左鏈接向下進(jìn)行變換，刪除最大元素算法會(huì)一直沿著右鏈接向下進(jìn)行變換，而刪除任意元素算法需要同時(shí)存在著左右鏈接向下進(jìn)行變換。?刪除任意元素算法需要先進(jìn)行命中查找，在命中查找的過程中會(huì)進(jìn)行沿著左右鏈接向下變換，如果查找命中則將右子樹的最小元素替換掉待刪除元素，然后進(jìn)行右子樹的刪除最小元素算法；如果查找未命中，則直接返回balance函數(shù)，向上將3-節(jié)點(diǎn)左傾或?qū)?-節(jié)點(diǎn)配平。?Code：刪除任意元素算法?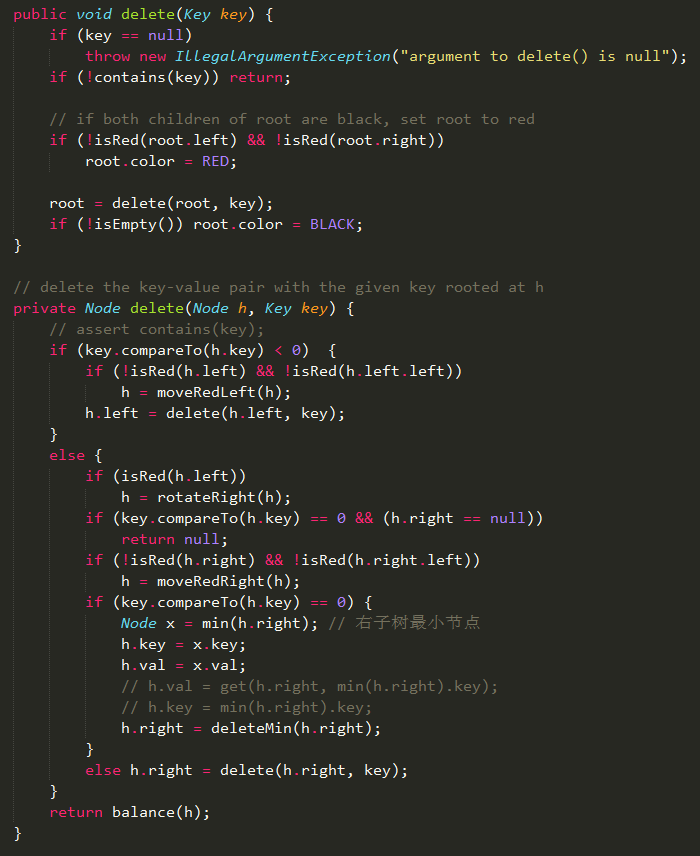
?動(dòng)畫：2-3-4樹與紅黑樹的刪除?
學(xué)習(xí)完上面的算法之后，可以總結(jié)下紅黑樹的性質(zhì)：?1）每個(gè)節(jié)點(diǎn)或是紅色的，或是黑色的；?2）根節(jié)點(diǎn)是黑色的；?3）每個(gè)葉子節(jié)點(diǎn)（NIL）是黑色的；?4）如果一個(gè)節(jié)點(diǎn)是紅色的，則它的兩個(gè)子節(jié)點(diǎn)都是黑色的（NIL節(jié)點(diǎn)也是黑色的）；?5）對(duì)每個(gè)結(jié)點(diǎn)，從該節(jié)點(diǎn)到其所有后代葉子節(jié)點(diǎn)的簡單路徑上，均包含相同數(shù)目的黑色節(jié)點(diǎn)（黑鏈接平衡）。
作者：我脫下短袖
二分搜索樹是為了快速查找而生，它是一顆二叉樹，每一個(gè)節(jié)點(diǎn)只有一個(gè)元素（值或鍵值對(duì)），左子樹所有節(jié)點(diǎn)的值均小于父節(jié)點(diǎn)的值，右子樹所有的值均大于父節(jié)點(diǎn)的值，左右子樹也是一顆二分搜索樹，而且沒有鍵值相等的節(jié)點(diǎn)。它的查找、插入和刪除的時(shí)間復(fù)雜度都與樹高成比例，期望值是O(logn)。
但是插入數(shù)組如[15，17，13，12，9，7]，二分搜索樹就暴露了缺點(diǎn)，將樹退化成線性表，查找的時(shí)間復(fù)雜度達(dá)到最壞時(shí)間復(fù)雜度O(n)。?動(dòng)畫：二分搜索樹退化成線性表?
那有沒有插入和刪除操作都能保持樹的完美平衡性（任何一個(gè)節(jié)點(diǎn)到其葉子節(jié)點(diǎn)的路徑長度都是相等的）？?有，B樹。B樹是一種自平衡的樹，根節(jié)點(diǎn)到其葉子節(jié)點(diǎn)的路徑高度都是一樣的，能夠保持?jǐn)?shù)據(jù)有序（通過中序遍歷能得到有序數(shù)據(jù)）。B樹一個(gè)節(jié)點(diǎn)可以擁有2個(gè)以上的子樹，如2-3樹、2-3-4樹甚至2-3-4-5-6-7-8樹，它們滿足二分搜索樹的性質(zhì)，但它們不屬于二叉樹，也不屬于二分搜索樹。?2-3-4樹的完美平衡，每條從根節(jié)點(diǎn)到葉子節(jié)點(diǎn)的路徑的高度都是一樣的?2-3-4樹有以下節(jié)點(diǎn)組成：?2-節(jié)點(diǎn)，含有一個(gè)元素（值或鍵值對(duì)）和兩個(gè)子樹（左右子樹），左子樹所有的值均小于父節(jié)點(diǎn)的值，右子樹所有的值均大于父節(jié)點(diǎn)的值；?3-節(jié)點(diǎn)，含有兩個(gè)元素和三個(gè)子樹，左子樹所有的值均小于父節(jié)點(diǎn)最小元素的值，中間子樹所有的值均位于父節(jié)點(diǎn)兩個(gè)元素之間，右子樹所有的值均大于父節(jié)點(diǎn)最大元素的值；?4-節(jié)點(diǎn)，含有三個(gè)元素和四個(gè)子樹，節(jié)點(diǎn)之間的比較也滿足二分搜索樹的性質(zhì)。?2-3-4樹查找算法?2-3-4樹的查找類似二分搜索樹的查找。?2-3-4樹插入算法?2-3-4樹的插入算法是消除當(dāng)前節(jié)點(diǎn)是4-節(jié)點(diǎn)，將4-節(jié)點(diǎn)分解成多個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并成3-節(jié)點(diǎn)或4-節(jié)點(diǎn)。?沿著鏈接向下進(jìn)行變換分解4-節(jié)點(diǎn)分為兩種情況：?1）4-節(jié)點(diǎn)作為根節(jié)點(diǎn)，分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)作為根節(jié)點(diǎn)；?2）當(dāng)前節(jié)點(diǎn)為4-節(jié)點(diǎn)，分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并成3-節(jié)點(diǎn)或4-節(jié)點(diǎn)；?
圖：沿著鏈接向下進(jìn)行變換，分解4-節(jié)點(diǎn)?在沿著左右鏈接向下進(jìn)行變換的同時(shí)，也會(huì)進(jìn)行命中查找。如果元素是鍵值對(duì)的話，查找命中將舊的值賦值為新的值；如果元素是一個(gè)值的話，查找命中將忽略之，因?yàn)槎炙阉鳂湫枰獫M足沒有相等的元素；如果需要支持重復(fù)的元素，則在元素對(duì)象添加count屬性，默認(rèn)為1。?如果查找未命中，則將待插入元素插入在葉子節(jié)點(diǎn)上。樹底下插入一個(gè)元素只有兩種情況：向2-節(jié)點(diǎn)中插入和向3-節(jié)點(diǎn)中插入。?圖：樹底下插入一個(gè)元素?2-3-4樹刪除算法?2-3-4樹的刪除算法是消除當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，向兄弟節(jié)點(diǎn)或父節(jié)點(diǎn)借一個(gè)元素過來。?刪除最小元素?從根節(jié)點(diǎn)的左孩子開始，沿著左鏈接向下進(jìn)行變換可以分為三種情況：?1）當(dāng)前節(jié)點(diǎn)不是2-節(jié)點(diǎn)，跳過；?2）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，將當(dāng)前節(jié)點(diǎn)、父節(jié)點(diǎn)最小元素和兄弟節(jié)點(diǎn)合并為4-節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成4-節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，將兄弟節(jié)點(diǎn)的最小元素移到父節(jié)點(diǎn)，父節(jié)點(diǎn)的最小元素移到當(dāng)前節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成3-節(jié)點(diǎn)。?圖：沿著左鏈接向下進(jìn)行變換?刪除最大元素?從根節(jié)點(diǎn)的右孩子開始，沿著右鏈接向下進(jìn)行變換也同樣分為三種情況：?1）當(dāng)前節(jié)點(diǎn)不是2-節(jié)點(diǎn)，跳過；?2）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，將當(dāng)前節(jié)點(diǎn)、父節(jié)點(diǎn)的最大元素和兄弟節(jié)點(diǎn)合并為4-節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成4-節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)是2-節(jié)點(diǎn)，兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，將兄弟節(jié)點(diǎn)的最大元素移到父節(jié)點(diǎn)，父節(jié)點(diǎn)的最大元素移到當(dāng)前節(jié)點(diǎn)，當(dāng)前節(jié)點(diǎn)變換成3-節(jié)點(diǎn)。?圖：沿著右鏈接向下進(jìn)行變換?刪除任意元素?學(xué)習(xí)過刪除最小元素和刪除最大元素算法之后，刪除任意元素的算法自然就簡單了。刪除任意元素算法需要先進(jìn)行命中查找，若查找命中，則將右子樹的最小值替換掉待刪除元素，然后將右子樹進(jìn)行刪除最小元素的算法。?2-3-4樹雖滿足二分搜索樹的性質(zhì)，但不是一顆二分搜索樹。如果期望它是一顆二分搜索樹，就需要將3-節(jié)點(diǎn)和4-節(jié)點(diǎn)替換為多個(gè)2-節(jié)點(diǎn)，還需要注明元素之間的關(guān)系（用紅鏈接表示）。?替換3-節(jié)點(diǎn)和4-節(jié)點(diǎn)?圖：替換3-節(jié)點(diǎn)?圖：替換4-節(jié)點(diǎn)?但是存在一個(gè)問題，2-3-4樹因?yàn)?-節(jié)點(diǎn)的不同表示會(huì)有很多種不同的紅黑樹，3-節(jié)點(diǎn)既可以左傾，也可以右傾。所以為了保證樹的唯一性，3-節(jié)點(diǎn)只考慮左傾，當(dāng)然你也可以只考慮右傾。?這樣對(duì)于任何一顆2-3-4樹，只考慮左傾的情況下，都能得到唯一的一顆對(duì)應(yīng)的紅黑樹，這種樹也叫左傾紅黑樹，相對(duì)比較減少了復(fù)雜性，設(shè)計(jì)更容易被實(shí)現(xiàn)。?紅黑樹查找算法?紅黑樹的查找算法和二分搜索樹一樣。?關(guān)于鏈接的顏色變換只跟顏色轉(zhuǎn)換有關(guān)，而旋轉(zhuǎn)不會(huì)改變鏈接的顏色變換，只在被紅鏈接指向的節(jié)點(diǎn)變成紅色，被黑鏈接指向的節(jié)點(diǎn)變成黑色。?旋轉(zhuǎn)?旋轉(zhuǎn)是將不滿足紅黑樹性質(zhì)的3-節(jié)點(diǎn)和4-節(jié)點(diǎn)進(jìn)行旋轉(zhuǎn)，如果3-節(jié)點(diǎn)出現(xiàn)右鏈接，則將右鏈接通過左旋轉(zhuǎn)變成左鏈接；如果4-節(jié)點(diǎn)出現(xiàn)一個(gè)紅節(jié)點(diǎn)連著兩條紅鏈接，則將4-節(jié)點(diǎn)配平。?左旋轉(zhuǎn)?圖：左旋轉(zhuǎn)?右旋轉(zhuǎn)?圖：右旋轉(zhuǎn)?圖：3-節(jié)點(diǎn)和4-節(jié)點(diǎn)的旋轉(zhuǎn)?Code：右旋轉(zhuǎn)和左旋轉(zhuǎn)??顏色轉(zhuǎn)換?顏色轉(zhuǎn)換只應(yīng)用于4-節(jié)點(diǎn)。?圖：顏色轉(zhuǎn)換?Code：顏色轉(zhuǎn)換??紅黑樹插入算法?回顧之前的2-3-4樹的插入算法，它有兩個(gè)過程：沿著鏈接向下進(jìn)行分解4-節(jié)點(diǎn)和樹底下插入一個(gè)元素。?紅黑樹的插入算法和2-3-4樹的插入算法類似，它不僅包含前面兩個(gè)過程，還增加了向上進(jìn)行變換的過程，此過程是將3-節(jié)點(diǎn)左傾和4-節(jié)點(diǎn)配平。?紅黑樹插入算法會(huì)先從根節(jié)點(diǎn)開始，沿著左右鏈接向下進(jìn)行變換，目的是為了分解4-節(jié)點(diǎn)。如果該節(jié)點(diǎn)的左右孩子都是紅節(jié)點(diǎn)，則通過flipColors方法進(jìn)行顏色轉(zhuǎn)換，接著進(jìn)行下一個(gè)子節(jié)點(diǎn)；如果不是，則直接進(jìn)行下一個(gè)子節(jié)點(diǎn)。?到達(dá)樹底的時(shí)候，則意味著可以開始插入新的元素。?如果紅黑樹目前是一顆空樹，插入紅色的元素作為第一個(gè)節(jié)點(diǎn)，然后該節(jié)點(diǎn)變成黑色。如果不是一顆空樹，插入元素分為三種情況：向2-節(jié)點(diǎn)插入新元素、向3-節(jié)點(diǎn)插入新元素和向4-節(jié)點(diǎn)插入新元素。?向2-節(jié)點(diǎn)插入新元素?向2-節(jié)點(diǎn)插入新元素很簡單，如果新元素的值小于父節(jié)點(diǎn)，直接插入紅色的節(jié)點(diǎn)即可；如果新元素的值大于父節(jié)點(diǎn)，則產(chǎn)生一個(gè)紅色右鏈接，插完之后則將3-節(jié)點(diǎn)進(jìn)行左旋轉(zhuǎn)，將右鏈接變成左鏈接，被紅鏈接指向的節(jié)點(diǎn)變成紅色，被黑鏈接指向的節(jié)點(diǎn)變成黑色。?圖：向2-節(jié)點(diǎn)插入新元素?向3-節(jié)點(diǎn)插入新元素?因?yàn)榍懊娴?-節(jié)點(diǎn)進(jìn)行過旋轉(zhuǎn)，此時(shí)的3-節(jié)點(diǎn)肯定滿足左傾紅黑樹的性質(zhì)。向3-節(jié)點(diǎn)插入新元素分為三種情況：?1）新元素的值位于3-節(jié)點(diǎn)中的兩元素之間；?2）新元素的值小于3-節(jié)點(diǎn)中的最小元素；?3）新元素的值大于3-節(jié)點(diǎn)中的最大元素。?圖：向3-節(jié)點(diǎn)插入新元素?向4-節(jié)點(diǎn)插入新元素?向4-節(jié)點(diǎn)插入新元素之前需要先進(jìn)行顏色轉(zhuǎn)換，才可以進(jìn)行插入新的元素。?圖：向4-節(jié)點(diǎn)插入新元素?插完新元素之后需要滿足紅黑樹的性質(zhì)，則在沿著父節(jié)點(diǎn)的鏈接向上進(jìn)行變換，具體做法和向3-節(jié)點(diǎn)插入新元素的做法類似，通過左旋轉(zhuǎn)將3-節(jié)點(diǎn)左傾和左右旋轉(zhuǎn)將4-節(jié)點(diǎn)配平，沒有顏色轉(zhuǎn)換。?動(dòng)畫：2-3-4樹與紅黑樹的插入?Code：紅黑樹插入算法?
?紅黑樹刪除算法?紅黑樹刪除算法也需要進(jìn)行旋轉(zhuǎn)和顏色轉(zhuǎn)換操作，在插入算法中為了待插入元素所在的節(jié)點(diǎn)不是4-節(jié)點(diǎn)，所以在沿著左右鏈接向下進(jìn)行變換時(shí)將4-節(jié)點(diǎn)分解成3個(gè)2-節(jié)點(diǎn)，中間的2-節(jié)點(diǎn)與父節(jié)點(diǎn)合并；而在刪除算法中為了待刪除元素所在的節(jié)點(diǎn)不是2-節(jié)點(diǎn)，所以在沿著左右鏈接向下進(jìn)行變換時(shí)將2-節(jié)點(diǎn)向其它不是2-節(jié)點(diǎn)的節(jié)點(diǎn)（兄弟節(jié)點(diǎn)或父節(jié)點(diǎn)）借一個(gè)元素過來，合并成3-節(jié)點(diǎn)。?所以，只要是2-節(jié)點(diǎn)的節(jié)點(diǎn)，如果兄弟節(jié)點(diǎn)不是2-節(jié)點(diǎn)，就將兄弟節(jié)點(diǎn)的與父節(jié)點(diǎn)鄰近的元素移到父節(jié)點(diǎn)，而父節(jié)點(diǎn)將與當(dāng)前節(jié)點(diǎn)鄰近的元素移到當(dāng)前節(jié)點(diǎn)；如果兄弟節(jié)點(diǎn)是2-節(jié)點(diǎn)，則將父節(jié)點(diǎn)的與當(dāng)前節(jié)點(diǎn)鄰近的元素移到當(dāng)前節(jié)點(diǎn)。（是不是很繞？待會(huì)在后面刪除最值算法中詳細(xì)給出）?然后刪除完一個(gè)元素之后需要進(jìn)行修復(fù)調(diào)整，將這個(gè)樹滿足紅黑樹的性質(zhì)。如果右鏈接是紅色，將右鏈接通過左旋轉(zhuǎn)變成左鏈接；如果有連續(xù)的左鏈接，通過右旋轉(zhuǎn)配平，然后進(jìn)行顏色轉(zhuǎn)換。?Code：向上變換（修復(fù)調(diào)整）??刪除最小元素?刪除最小元素算法和二分搜索樹一樣，一直遞歸它的左孩子，直到它的左孩子為空才進(jìn)行刪除這個(gè)最小元素。但是紅黑樹在遞歸的同時(shí)如何旋轉(zhuǎn)和顏色轉(zhuǎn)換是個(gè)問題。?刪除最小元素算法一直沿著左鏈接向下進(jìn)行轉(zhuǎn)換，對(duì)照2-3-4樹，我們可以給出三種情況，從根節(jié)點(diǎn)開始：?1）當(dāng)前節(jié)點(diǎn)（父節(jié)點(diǎn)位置）的左子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，直接進(jìn)行下一個(gè)節(jié)點(diǎn)（左子節(jié)點(diǎn)）；?2）當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)和右子節(jié)點(diǎn)都是2-節(jié)點(diǎn)，則將左子節(jié)點(diǎn)、當(dāng)前節(jié)點(diǎn)的最小元素和右子節(jié)點(diǎn)合并成4-節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)的左子節(jié)點(diǎn)是2-節(jié)點(diǎn)，右子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，則將右子節(jié)點(diǎn)的最小元素移到當(dāng)前節(jié)點(diǎn)的位置，當(dāng)前節(jié)點(diǎn)的最小元素移到左子節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)。?圖：沿著左鏈接向下進(jìn)行轉(zhuǎn)換?Code：沿著左鏈接向下變換??直到某元素左孩子為空的時(shí)候，此時(shí)的元素是這個(gè)樹的最小元素。因?yàn)橥ㄟ^前面的轉(zhuǎn)換，最小元素肯定被一個(gè)紅鏈接指向，刪除這個(gè)元素之后通過balance方法修復(fù)調(diào)整為紅黑樹。?Code：刪除最小元素算法??刪除最大元素?刪除最大元素算法和刪除最小元素算法類似的，也分為三種情況：?1）當(dāng)前節(jié)點(diǎn)（父節(jié)點(diǎn)位置）的右子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，直接進(jìn)行下一個(gè)節(jié)點(diǎn)（右子節(jié)點(diǎn)）；?2）當(dāng)前節(jié)點(diǎn)的右子節(jié)點(diǎn)和左子節(jié)點(diǎn)都是2-節(jié)點(diǎn)，則將右子節(jié)點(diǎn)、當(dāng)前節(jié)點(diǎn)的最大元素和左子節(jié)點(diǎn)合并成4-節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)；?3）當(dāng)前節(jié)點(diǎn)的右子節(jié)點(diǎn)是2-節(jié)點(diǎn)，左子節(jié)點(diǎn)不是2-節(jié)點(diǎn)，則將左子節(jié)點(diǎn)的最大元素移到當(dāng)前節(jié)點(diǎn)的位置，當(dāng)前節(jié)點(diǎn)的最大元素移到左子節(jié)點(diǎn)，然后進(jìn)行下一個(gè)節(jié)點(diǎn)。?圖：沿著右鏈接向下進(jìn)行變換?Code：沿著右鏈接向下變換??Code：刪除最大元素算法??刪除任意元素?學(xué)習(xí)過前面的刪除最小元素算法和刪除最大元素算法，刪除任意元素會(huì)變得很簡單。刪除最小元素算法會(huì)一直沿著左鏈接向下進(jìn)行變換，刪除最大元素算法會(huì)一直沿著右鏈接向下進(jìn)行變換，而刪除任意元素算法需要同時(shí)存在著左右鏈接向下進(jìn)行變換。?刪除任意元素算法需要先進(jìn)行命中查找，在命中查找的過程中會(huì)進(jìn)行沿著左右鏈接向下變換，如果查找命中則將右子樹的最小元素替換掉待刪除元素，然后進(jìn)行右子樹的刪除最小元素算法；如果查找未命中，則直接返回balance函數(shù)，向上將3-節(jié)點(diǎn)左傾或?qū)?-節(jié)點(diǎn)配平。?Code：刪除任意元素算法??動(dòng)畫：2-3-4樹與紅黑樹的刪除?學(xué)習(xí)完上面的算法之后，可以總結(jié)下紅黑樹的性質(zhì)：?1）每個(gè)節(jié)點(diǎn)或是紅色的，或是黑色的；?2）根節(jié)點(diǎn)是黑色的；?3）每個(gè)葉子節(jié)點(diǎn)（NIL）是黑色的；?4）如果一個(gè)節(jié)點(diǎn)是紅色的，則它的兩個(gè)子節(jié)點(diǎn)都是黑色的（NIL節(jié)點(diǎn)也是黑色的）；?5）對(duì)每個(gè)結(jié)點(diǎn)，從該節(jié)點(diǎn)到其所有后代葉子節(jié)點(diǎn)的簡單路徑上，均包含相同數(shù)目的黑色節(jié)點(diǎn)（黑鏈接平衡）。
推薦閱讀
評(píng)論
圖片
表情