?PDF、CDF、CCDF圖的區(qū)別

PDF：連續(xù)型隨機(jī)變量的概率密度函數(shù)是一個(gè)描述這個(gè)隨機(jī)變量的輸出值,在某個(gè)確定的取值點(diǎn)附近的可能性的函數(shù)。

概率密度函數(shù)，描述可能性的變化情況，比如正態(tài)分布密度函數(shù)，給定一個(gè)值, 判斷這個(gè)值在該正態(tài)分布中所在的位置后, 獲得其他數(shù)據(jù)高于該值或低于該值的比例。

CDF：能完整描述一個(gè)實(shí)數(shù)隨機(jī)變量x的概率分布，是概率密度函數(shù)的積分。隨機(jī)變量小于或者等于某個(gè)數(shù)值的概率P（X<=x）即：F(x) = P(X<=x)。

可使用 CDF 確定取自總體的隨機(jī)觀測(cè)值將小于或等于特定值的概率。還可以使用此信息來(lái)確定觀測(cè)值將大于特定值或介于兩個(gè)值之間的概率。

對(duì)于所有實(shí)數(shù)x,CDF（cumulative distribution function）,與概率密度函數(shù)PDF(probability density function）相對(duì)。任何一個(gè)CDF，是一個(gè)不減函數(shù)，累積和為1。累計(jì)分段概率值就是所有比給定x小的數(shù)在數(shù)據(jù)集中所占的比例。任意特定點(diǎn)處的填充x的 CDF 等于 PDF 曲線下直至該點(diǎn)左側(cè)陰影面積。

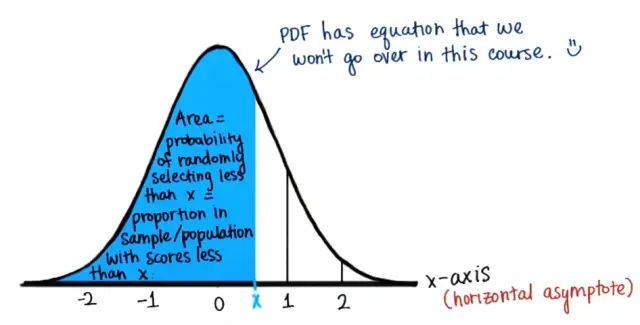
←概率密度函數(shù)PDF→

圖中陰影面積=隨機(jī)選擇一個(gè)小于x的值的概率=總體中小于x的所有值所占比例

上面的pdf描述了CDF的變化趨勢(shì)，即曲線的斜率。

CCDF：互補(bǔ)累積分布函數(shù)（complementary cumulative distribution function），是對(duì)連續(xù)函數(shù)，所有大于a的值，其出現(xiàn)概率的和。CDF 曲線從 0% 的概率上升到 100% 的概率，而 CCDF 曲線則從 100% 的概率下降到 0% 的概率。

累積分布函數(shù)（CDF）=∫PDF（曲線下的面積 = 1 或 100%）。

互補(bǔ)累積分布函數(shù)（CCDF）= 1-CDF。

?PDF與CDF對(duì)比示意圖

在 Python 中使用scipy.stats.norm.ppf()計(jì)算 CDF

import?numpy?as?np
from?scipy.stats?import?norm
import?matplotlib.pyplot?as?plt

#?均值10，方差1,正態(tài)分布模擬數(shù)據(jù)
data?=?np.random.normal(10,?1,?100)

#計(jì)算正態(tài)概率密度函數(shù)在x處的值
def?norm_dist_prob(theta):
????y?=?norm.pdf(theta,?loc=np.mean(data),?scale=np.std(data))
????return?y

#計(jì)算正態(tài)分布累積概率值
def?norm_dist_cdf(theta):
????y?=?norm.cdf(theta,loc=10,scale=1)
????return?y
????
#利用ppf找到適合的橫坐標(biāo)，百分點(diǎn)函數(shù)
#ppf分位點(diǎn)函數(shù)（CDF的逆）即累計(jì)分布函數(shù)的逆函數(shù)（分位點(diǎn)函數(shù)，給出分位點(diǎn)返回對(duì)應(yīng)的x值）。
#scipy.stats.norm.ppf(0.95， loc=0，scale=1)返回累積分布函數(shù)中概率等于0.95對(duì)應(yīng)的x值（CDF函數(shù)中已知y求對(duì)應(yīng)的x）。
x?=?np.linspace(norm.ppf(0.01,loc=np.mean(data),?scale=np.std(data)),
????????????????norm.ppf(0.99,loc=np.mean(data),?scale=np.std(data)),?len(data))??#linspace()?函數(shù)返回指定間隔內(nèi)均勻間隔數(shù)字的 ndarray。

y1=norm_dist_prob(x)
y2=norm_dist_cdf(x)
plt.plot(x,?y1,'g',label='pdf')
plt.plot(x,?y2,'r',label='cdf')
plt.show()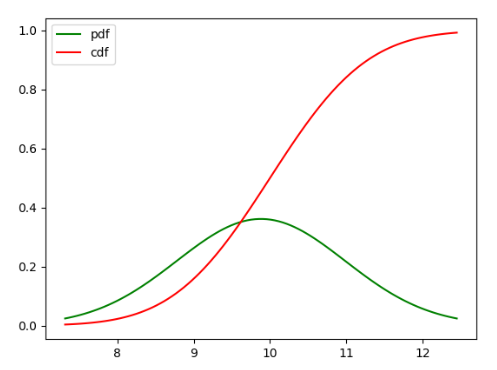

←PDF與CDF分布曲線對(duì)比→

Python中計(jì)算累積分布函數(shù)

利用某設(shè)備三種工況條件下監(jiān)測(cè)時(shí)間序列數(shù)據(jù)，對(duì)比分析不同工況下設(shè)備運(yùn)行性能差異。這里數(shù)據(jù)大家可自行構(gòu)造測(cè)試。

#CDF數(shù)據(jù)處理
def?Cumsum_cdf(DATA):
????denominator?=?len(DATA['VALS'])
????Data1?=?pd.Series(DATA['VALS'])

????#?#利用value_counts方法進(jìn)行分組頻數(shù)計(jì)算
????Fre=Data1.value_counts()
????#?#對(duì)獲得的表格整體按照索引自小到大進(jìn)行排序
????Fre_sort=Fre.sort_index(axis=0,ascending=True)
????#?#?每個(gè)數(shù)據(jù)出現(xiàn)頻數(shù)除以數(shù)據(jù)總數(shù)才能獲得該數(shù)據(jù)的概率
????#?#重置表格索引
????Fre_df=Fre_sort.reset_index()
????#?#將頻數(shù)轉(zhuǎn)換成概率
????Fre_df['VALS']=Fre_df['VALS']/denominator
????#?#將列表列索引重命名
????Fre_df.columns=['Rds','Fre']

????#?#?將數(shù)據(jù)列表從小到大排列，然后將每個(gè)數(shù)據(jù)出現(xiàn)的概率進(jìn)行疊加
????#?#利用cumsum函數(shù)進(jìn)行概率的累加并按照順序添加到表格中
????Fre_df['cumsum']=np.cumsum(Fre_df['Fre'])

????return?Fre_df
????
def?Cumulative_Distribution_Function(DATA,VAL1?=300):
????import?matplotlib.pyplot?as?plt
????from?scipy.special?import?jn,?jn_zeros
????plt.rcParams['font.sans-serif']?=?['SimHei']??#?用來(lái)正常顯示中文標(biāo)簽
????plt.rcParams['axes.unicode_minus']?=?False??#?用來(lái)正常顯示負(fù)號(hào)

????df_A1,df_A2,df_A3?=?DATA
????#cdf數(shù)據(jù)處理函數(shù),添加三條曲線
????Fre_A1?=?Cumsum_cdf(df_A1[df_A1.VALS?>?0])
????Fre_A2?=?Cumsum_cdf(df_A2[df_A2.VALS?>?0])
????Fre_A3?=?Cumsum_cdf(df_A3[df_A3.VALS?>?0])

????#?創(chuàng)建畫布，只有一張圖，也可以多張
????#?plot?=?plt.figure()
????fig,?ax1=?plt.subplots(figsize=(8,?4),?dpi=200)
????ax1.spines["right"].set_visible(False)
????ax1.spines["top"].set_visible(False)
????ax1.grid(ls="--",?lw=0.25,?color="#4E616C")

????#?按照Rds列為橫坐標(biāo)，累計(jì)概率分布為縱坐標(biāo)作圖
????#添加三條數(shù)據(jù)曲線
????ax1.plot(Fre_A1['Rds'],?Fre_A1['cumsum'],?label=f'工況1',?mfc="white",?ms=5)
????ax1.plot(Fre_A2['Rds'],?Fre_A2['cumsum'],?label=f'工況2',?mfc="white",?ms=5)
????ax1.plot(Fre_A3['Rds'],?Fre_A3['cumsum'],?label=f'工況3',?mfc="white",?ms=5)


????#?#?圖的標(biāo)題
????ax1.legend(loc='upper?left',
??????????????frameon=False,
??????????????edgecolor="None",fontsize=8)

????#峰值負(fù)載
????upper_peak?=?max(Fre_A1['Rds'].max(),Fre_A2['Rds'].max(),Fre_A3['Rds'].max())

????f1_A25?=?Fre_A3[Fre_A3['Rds']?/?VAL1?>=?0.25]["cumsum"].to_list()[0]
????f1_A50?=?Fre_A3[Fre_A3['Rds']?/?VAL1?>=?0.5]["cumsum"].to_list()[0]

????#?#?顯示坐標(biāo)點(diǎn)橫線、豎線
????peak?=?round(upper_peak/VAL1,2)*100
????
????#?#?峰值點(diǎn)負(fù)載率
????ax1.annotate(
????????f"$({peak}$%$,100$%$)$",?#?標(biāo)注文字
????????(upper_peak,1),
????????#?size="small",#medium
????????xytext=(-65,?-40),
????????textcoords="offset?points",
????????fontsize=10,
????????arrowprops=dict(
????????????arrowstyle="->",
????????????connectionstyle="arc3,rad=-0.3"),?)

????#25%、50%分界線
????plt.vlines(VAL1?*?0.25,?0,f1_A25,?colors="c",?linestyles="dashed")

????plt.vlines(VAL1?*?0.5,?0,?f1_A50,?colors="c",?linestyles="dashed")

????#峰值線
????plt.vlines(upper_peak,?0,1,colors="r",?linestyles="dashed")


????#添加陰影區(qū)域，工況1
????X?=?Fre_A1['Rds'].tolist()
????C?=?Fre_A1['cumsum'].tolist()
????x?=?np.array([i?for?i?in?X])
????plt.fill_between(x,C,where=(VAL1*0.5*0.8?'green')

????#標(biāo)注工況3,50%負(fù)載概率值
????ax1.annotate(
????????f"$(50$%$,{round(f1_A50,2)*100}$%$)$",?#?標(biāo)注文字
????????(VAL1*0.5,f1_A50),
????????#?size="small",#medium
????????xytext=(-65,?-40),
????????textcoords="offset?points",
????????fontsize=10,
????????arrowprops=dict(
????????????arrowstyle="->",
????????????connectionstyle="arc3,rad=-0.3"),?)

????#標(biāo)注分界線名稱
????ax1.text(
????????VAL1?*?0.27,?0.10,
????????f'25%負(fù)載率界限',
????????va="top",?ha="left",
????????size=8)

????ax1.text(
????????VAL1?*?0.52,?0.10,
????????f'50%負(fù)載率界限',
????????va="top",?ha="left",
????????size=8)

????#主題名稱
????team_?=?ax1.text(
????????x=0,?y=ax1.get_ylim()[1]?+?ax1.get_ylim()[1]?/?20,
????????s=f"Cumulative?probability",
????????color="#4E616C",
????????va='center',
????????ha='left',
????????size=8
????)
????#?橫軸名
????ax1.set_xlabel("用電量（kWh）",fontsize?=8)

????plt.savefig(r".\test.png",bbox_inches="tight")

????return?plt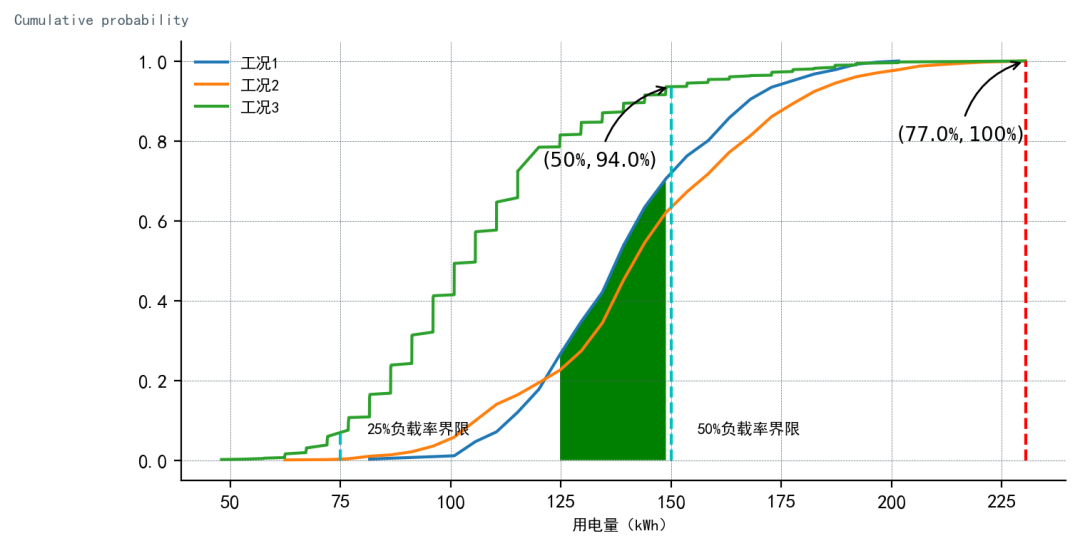

←某設(shè)備不同工況實(shí)際用能運(yùn)行曲線對(duì)比→

利用 CDF（概率累積分布函數(shù)）分析數(shù)據(jù)集分布情況。分析概率分布函數(shù)曲線可以快速、簡(jiǎn)明地描述并量化由不同工況下導(dǎo)致的長(zhǎng)期電能消耗中的細(xì)節(jié)差異。

注：

1、數(shù)據(jù)形式--dataframe

#?外部導(dǎo)入數(shù)據(jù)
DF?=?pd.read_excel(r".\ST\分析數(shù)據(jù).xlsx")
df_A1?=?DF[["工況1"]].copy()
df_A1?=?df_A1.rename(columns={'工況1':?'VALS'})
df_A2?=?DF[["工況2"]].copy()
df_A2?=?df_A2.rename(columns={'工況2':?'VALS'})
df_A3?=?DF[["工況3"]].copy()
df_A3?=?df_A3.rename(columns={'工況3':?'VALS'})
DATA?=?df_A1,df_A2,df_A3

VAL1?=300，VAL1這里表示設(shè)備功率值,其通常也作為異常參考閾值。這里不展開(kāi)業(yè)務(wù)相關(guān)分析。

2、標(biāo)注角度可按下圖調(diào)整，更多.annotate（）參數(shù)用法可上網(wǎng)查詢。

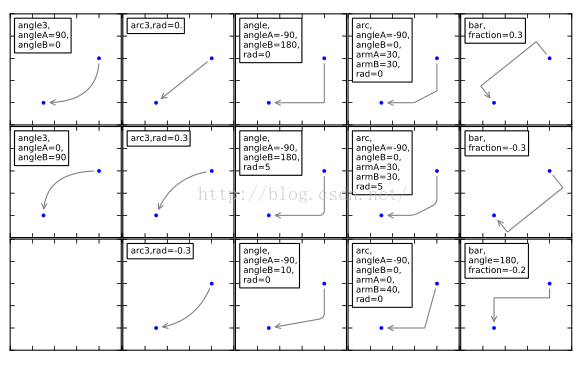
3、圖形美化自定義---參考以往推文一圖勝千言，圖解Matplotlib ！

??點(diǎn)擊關(guān)注｜設(shè)為星標(biāo)｜干貨速遞??

Python中概率累計(jì)分布函數(shù)（CDF）分析