【Python】Python實(shí)現(xiàn) 8 個(gè)概率分布公式及可視化
在本文中,我們將介紹一些常見的分布并通過Python 代碼進(jìn)行可視化以直觀地顯示它們。
現(xiàn)實(shí)世界中有幾個(gè)現(xiàn)象實(shí)例被認(rèn)為是統(tǒng)計(jì)性質(zhì)的(即天氣數(shù)據(jù)、銷售數(shù)據(jù)、財(cái)務(wù)數(shù)據(jù)等)。這意味著在某些情況下,我們已經(jīng)能夠開發(fā)出方法來幫助我們通過可以描述數(shù)據(jù)特征的數(shù)學(xué)函數(shù)來模擬自然。
“概率分布是一個(gè)數(shù)學(xué)函數(shù),它給出了實(shí)驗(yàn)中不同可能結(jié)果的發(fā)生概率。”
了解數(shù)據(jù)的分布有助于更好地模擬我們周圍的世界。它可以幫助我們確定各種結(jié)果的可能性,或估計(jì)事件的可變性。所有這些都使得了解不同的概率分布在數(shù)據(jù)科學(xué)和機(jī)器學(xué)習(xí)中非常有價(jià)值。
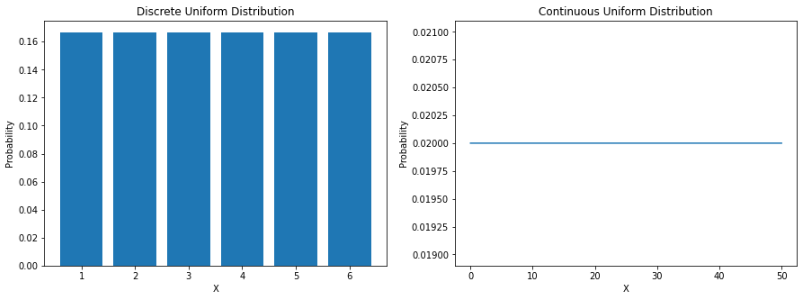
均勻分布
最直接的分布是均勻分布。均勻分布是一種概率分布,其中所有結(jié)果的可能性均等。例如,如果我們擲一個(gè)公平的骰子,落在任何數(shù)字上的概率是 1/6。這是一個(gè)離散的均勻分布。
但是并不是所有的均勻分布都是離散的——它們也可以是連續(xù)的。它們可以在指定范圍內(nèi)取任何實(shí)際值。a 和 b 之間連續(xù)均勻分布的概率密度函數(shù) (PDF) 如下:
讓我們看看如何在 Python 中對(duì)它們進(jìn)行編碼:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
# for continuous
a = 0
b = 50
size = 5000
X_continuous = np.linspace(a, b, size)
continuous_uniform = stats.uniform(loc=a, scale=b)
continuous_uniform_pdf = continuous_uniform.pdf(X_continuous)
# for discrete
X_discrete = np.arange(1, 7)
discrete_uniform = stats.randint(1, 7)
discrete_uniform_pmf = discrete_uniform.pmf(X_discrete)
# plot both tables
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(15,5))
# discrete plot
ax[0].bar(X_discrete, discrete_uniform_pmf)
ax[0].set_xlabel("X")
ax[0].set_ylabel("Probability")
ax[0].set_title("Discrete Uniform Distribution")
# continuous plot
ax[1].plot(X_continuous, continuous_uniform_pdf)
ax[1].set_xlabel("X")
ax[1].set_ylabel("Probability")
ax[1].set_title("Continuous Uniform Distribution")
plt.show()
高斯分布
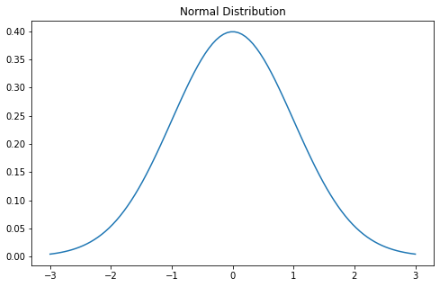
高斯分布可能是最常聽到也熟悉的分布。它有幾個(gè)名字:有人稱它為鐘形曲線,因?yàn)樗母怕蕡D看起來像一個(gè)鐘形,有人稱它為高斯分布,因?yàn)槭紫让枋鏊牡聡?guó)數(shù)學(xué)家卡爾·高斯命名,還有一些人稱它為正態(tài)分布,因?yàn)樵缙诘慕y(tǒng)計(jì)學(xué)家 注意到它一遍又一遍地再次發(fā)生。
正態(tài)分布的概率密度函數(shù)如下:
σ 是標(biāo)準(zhǔn)偏差,μ 是分布的平均值。要注意的是,在正態(tài)分布中,均值、眾數(shù)和中位數(shù)都是相等的。
當(dāng)我們繪制正態(tài)分布的隨機(jī)變量時(shí),曲線圍繞均值對(duì)稱——一半的值在中心的左側(cè),一半在中心的右側(cè)。并且,曲線下的總面積為 1。
mu = 0
variance = 1
sigma = np.sqrt(variance)
x = np.linspace(mu - 3*sigma, mu + 3*sigma, 100)
plt.subplots(figsize=(8, 5))
plt.plot(x, stats.norm.pdf(x, mu, sigma))
plt.title("Normal Distribution")
plt.show()
對(duì)于正態(tài)分布來說。經(jīng)驗(yàn)規(guī)則告訴我們數(shù)據(jù)的百分比落在平均值的一定數(shù)量的標(biāo)準(zhǔn)偏差內(nèi)。這些百分比是:
68% 的數(shù)據(jù)落在平均值的一個(gè)標(biāo)準(zhǔn)差內(nèi)。 95% 的數(shù)據(jù)落在平均值的兩個(gè)標(biāo)準(zhǔn)差內(nèi)。 99.7% 的數(shù)據(jù)落在平均值的三個(gè)標(biāo)準(zhǔn)差范圍內(nèi)。
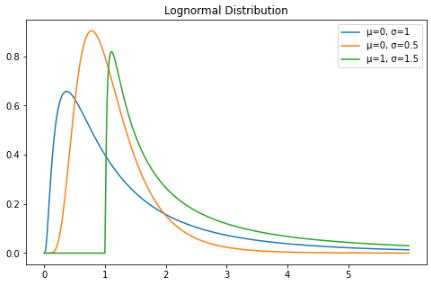
對(duì)數(shù)正態(tài)分布
對(duì)數(shù)正態(tài)分布是對(duì)數(shù)呈正態(tài)分布的隨機(jī)變量的連續(xù)概率分布。因此,如果隨機(jī)變量 X 是對(duì)數(shù)正態(tài)分布的,則 Y = ln(X) 具有正態(tài)分布。
這是對(duì)數(shù)正態(tài)分布的 PDF:
對(duì)數(shù)正態(tài)分布的隨機(jī)變量只取正實(shí)數(shù)值。因此,對(duì)數(shù)正態(tài)分布會(huì)創(chuàng)建右偏曲線。
讓我們?cè)?Python 中繪制它:
X = np.linspace(0, 6, 500)
std = 1
mean = 0
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
fig, ax = plt.subplots(figsize=(8, 5))
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=1")
ax.set_xticks(np.arange(min(X), max(X)))
std = 0.5
mean = 0
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=0, σ=0.5")
std = 1.5
mean = 1
lognorm_distribution = stats.lognorm([std], loc=mean)
lognorm_distribution_pdf = lognorm_distribution.pdf(X)
plt.plot(X, lognorm_distribution_pdf, label="μ=1, σ=1.5")
plt.title("Lognormal Distribution")
plt.legend()
plt.show()
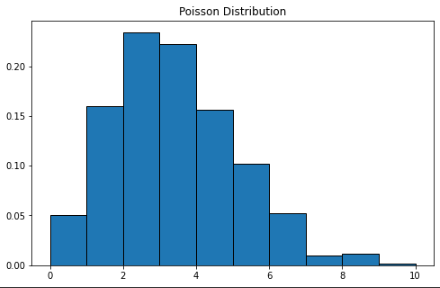
泊松分布
泊松分布以法國(guó)數(shù)學(xué)家西蒙·丹尼斯·泊松的名字命名。這是一個(gè)離散的概率分布,這意味著它計(jì)算具有有限結(jié)果的事件——換句話說,它是一個(gè)計(jì)數(shù)分布。因此,泊松分布用于顯示事件在指定時(shí)期內(nèi)可能發(fā)生的次數(shù)。
如果一個(gè)事件在時(shí)間上以固定的速率發(fā)生,那么及時(shí)觀察到事件的數(shù)量(n)的概率可以用泊松分布來描述。例如,顧客可能以每分鐘 3 次的平均速度到達(dá)咖啡館。我們可以使用泊松分布來計(jì)算 9 個(gè)客戶在 2 分鐘內(nèi)到達(dá)的概率。
下面是概率質(zhì)量函數(shù)公式:
λ 是一個(gè)時(shí)間單位的事件率——在我們的例子中,它是 3。k 是出現(xiàn)的次數(shù)——在我們的例子中,它是 9。這里可以使用 Scipy 來完成概率的計(jì)算。
from scipy import stats
print(stats.poisson.pmf(k=9, mu=3))
0.002700503931560479
泊松分布的曲線類似于正態(tài)分布,λ 表示峰值。
X = stats.poisson.rvs(mu=3, size=500)
plt.subplots(figsize=(8, 5))
plt.hist(X, density=True, edgecolor="black")
plt.title("Poisson Distribution")
plt.show()
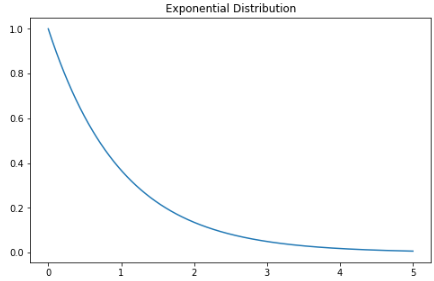
指數(shù)分布
指數(shù)分布是泊松點(diǎn)過程中事件之間時(shí)間的概率分布。指數(shù)分布的概率密度函數(shù)如下:
λ 是速率參數(shù),x 是隨機(jī)變量。
X = np.linspace(0, 5, 5000)
exponetial_distribtuion = stats.expon.pdf(X, loc=0, scale=1)
plt.subplots(figsize=(8,5))
plt.plot(X, exponetial_distribtuion)
plt.title("Exponential Distribution")
plt.show()
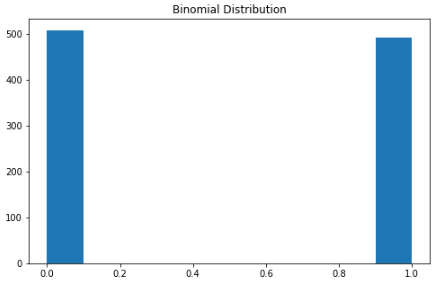
二項(xiàng)分布
可以將二項(xiàng)分布視為實(shí)驗(yàn)中成功或失敗的概率。有些人也可能將其描述為拋硬幣概率。
參數(shù)為 n 和 p 的二項(xiàng)式分布是在 n 個(gè)獨(dú)立實(shí)驗(yàn)序列中成功次數(shù)的離散概率分布,每個(gè)實(shí)驗(yàn)都問一個(gè)是 - 否問題,每個(gè)實(shí)驗(yàn)都有自己的布爾值結(jié)果:成功或失敗。
本質(zhì)上,二項(xiàng)分布測(cè)量?jī)蓚€(gè)事件的概率。一個(gè)事件發(fā)生的概率為 p,另一事件發(fā)生的概率為 1-p。
這是二項(xiàng)分布的公式:
P = 二項(xiàng)分布概率 = 組合數(shù) x = n次試驗(yàn)中特定結(jié)果的次數(shù) p = 單次實(shí)驗(yàn)中,成功的概率 q = 單次實(shí)驗(yàn)中,失敗的概率 n = 實(shí)驗(yàn)的次數(shù)
可視化代碼如下:
X = np.random.binomial(n=1, p=0.5, size=1000)
plt.subplots(figsize=(8, 5))
plt.hist(X)
plt.title("Binomial Distribution")
plt.show()
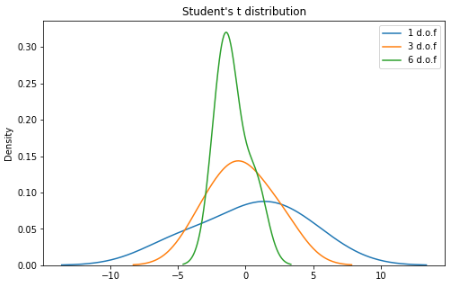
學(xué)生 t 分布
學(xué)生 t 分布(或簡(jiǎn)稱 t 分布)是在樣本量較小且總體標(biāo)準(zhǔn)差未知的情況下估計(jì)正態(tài)分布總體的均值時(shí)出現(xiàn)的連續(xù)概率分布族的任何成員。它是由英國(guó)統(tǒng)計(jì)學(xué)家威廉·西利·戈塞特(William Sealy Gosset)以筆名“student”開發(fā)的。
PDF如下:
n 是稱為“自由度”的參數(shù),有時(shí)可以看到它被稱為“d.o.f.” 對(duì)于較高的 n 值,t 分布更接近正態(tài)分布。
import seaborn as sns
from scipy import stats
X1 = stats.t.rvs(df=1, size=4)
X2 = stats.t.rvs(df=3, size=4)
X3 = stats.t.rvs(df=9, size=4)
plt.subplots(figsize=(8,5))
sns.kdeplot(X1, label = "1 d.o.f")
sns.kdeplot(X2, label = "3 d.o.f")
sns.kdeplot(X3, label = "6 d.o.f")
plt.title("Student's t distribution")
plt.legend()
plt.show()
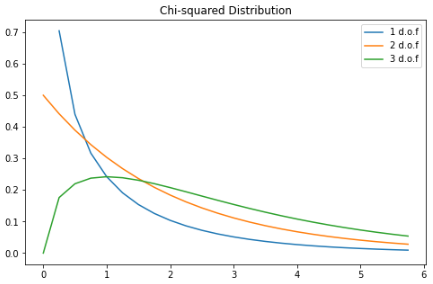
卡方分布
卡方分布是伽馬分布的一個(gè)特例;對(duì)于 k 個(gè)自由度,卡方分布是一些獨(dú)立的標(biāo)準(zhǔn)正態(tài)隨機(jī)變量的 k 的平方和。
PDF如下:
這是一種流行的概率分布,常用于假設(shè)檢驗(yàn)和置信區(qū)間的構(gòu)建。
在 Python 中繪制一些示例圖:
X = np.arange(0, 6, 0.25)
plt.subplots(figsize=(8, 5))
plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")
plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")
plt.plot(X, stats.chi2.pdf(X, df=3), label="3 d.o.f")
plt.title("Chi-squared Distribution")
plt.legend()
plt.show()
掌握統(tǒng)計(jì)學(xué)和概率對(duì)于數(shù)據(jù)科學(xué)至關(guān)重要。在本文展示了一些常見且常用的分布,希望對(duì)你有所幫助。
往期精彩回顧
適合初學(xué)者入門人工智能的路線及資料下載 (圖文+視頻)機(jī)器學(xué)習(xí)入門系列下載 機(jī)器學(xué)習(xí)及深度學(xué)習(xí)筆記等資料打印 《統(tǒng)計(jì)學(xué)習(xí)方法》的代碼復(fù)現(xiàn)專輯 機(jī)器學(xué)習(xí)交流qq群955171419,加入微信群請(qǐng)掃碼
