?常用的連續(xù)概率分布匯總

來源:Deephub IMBA 本文約1800字,建議閱讀5分鐘?
本文為你詳細介紹常用的連續(xù)概率分布。

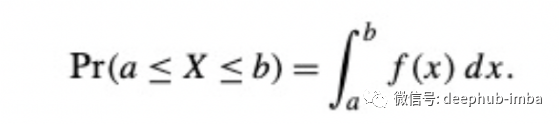
均勻分布


正態(tài)分布



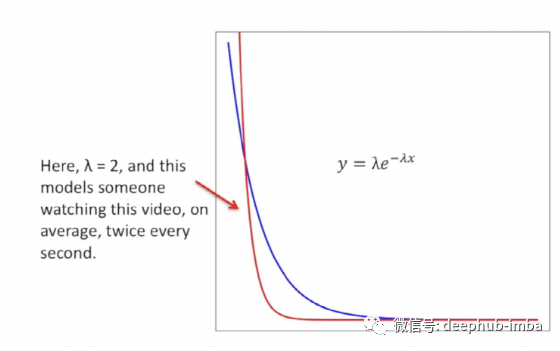
指數(shù)分布
t分布

伽瑪分布



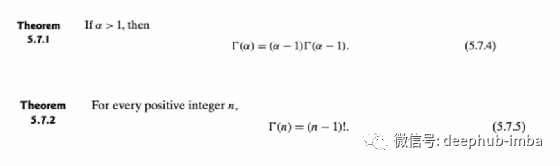
貝塔分布


F 分布
韋布爾分布
評論
圖片
表情
<b id="afajh"><abbr id="afajh"></abbr></b>
 下載APP
下載APP
來源:Deephub IMBA 本文約1800字,建議閱讀5分鐘?
本文為你詳細介紹常用的連續(xù)概率分布。

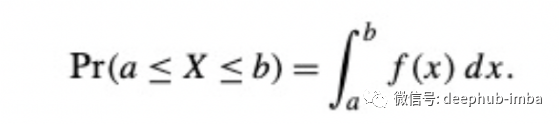










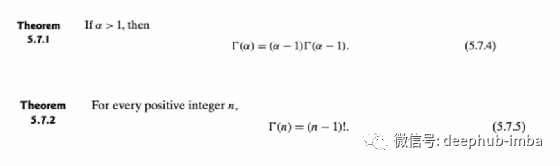


<b id="afajh"><abbr id="afajh"></abbr></b>