基于客戶細(xì)分的 K-Means 聚類算法（Python）
客群細(xì)分對于企業(yè)了解目標(biāo)受眾非常重要。根據(jù)受眾群體的不同，我們可以給采取不同的營銷策略。目前有許多無監(jiān)督的機(jī)器學(xué)習(xí)算法可以幫助公司識別他們的用戶群并創(chuàng)建消費(fèi)群體。
在本文中，我將分享一種目前比較流行的 K-Means 聚類的無監(jiān)督學(xué)習(xí)技術(shù)。K-Means的目標(biāo)是將所有可用的數(shù)據(jù)分組為彼此不同的不重疊的子組。K-Means聚類是數(shù)據(jù)科學(xué)家用來幫助公司進(jìn)行客戶細(xì)分的常用技術(shù)。
在本文中，你將了解以下內(nèi)容：
K-Means聚類的數(shù)據(jù)預(yù)處理 從頭構(gòu)建K-Means聚類算法 用于評估聚類模型性能的指標(biāo) 可視化構(gòu)建簇類 簇類構(gòu)建的解讀與分析
預(yù)備知識
在開始之前安裝以下庫：pandas、numpy、matplotlib、seaborn、sciket learn、kneed。完成后，我們就可以開始制作模型了！
本文中要的數(shù)據(jù)集可以文末下載，運(yùn)行以下代碼行以導(dǎo)入必要的庫并讀取數(shù)據(jù)集：
# Imports
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import sea
from kneed import KneeLocator
from sklearn.datasets import make_blobs
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
from mpl_toolkits.mplot3d import Axes3D
# reading the data frame
df = pd.read_csv('Mall_Customers.csv')
現(xiàn)在，讓我們看看數(shù)據(jù)：
df.head()
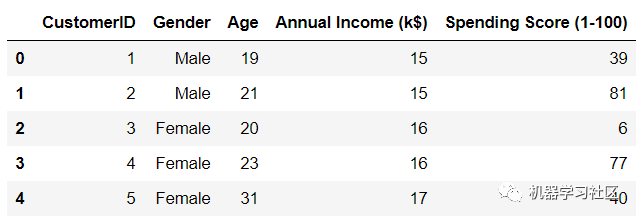數(shù)據(jù)集中有五個變量。CustomerID是數(shù)據(jù)集中每個客戶的唯一標(biāo)識符，我們可以刪除這個變量。它沒有為我們提供任何有用的集群信息。由于 gender 是一個分類變量，它需要編碼并轉(zhuǎn)換成數(shù)字。
在輸入模型之前，其他所有變量都將按正態(tài)分布進(jìn)行縮放。我們將標(biāo)準(zhǔn)化這些變量，平均值為0，標(biāo)準(zhǔn)偏差為1。
標(biāo)準(zhǔn)化變量
首先，讓我們標(biāo)準(zhǔn)化數(shù)據(jù)集中的所有變量，使它們在相同的范圍內(nèi)。
col_names = ['Annual Income (k$)', 'Age', 'Spending Score (1-100)']
features = df[col_names]
scaler = StandardScaler().fit(features.values)
features = scaler.transform(features.values)
scaled_features = pd.DataFrame(features, columns = col_names)
scaled_features.head()
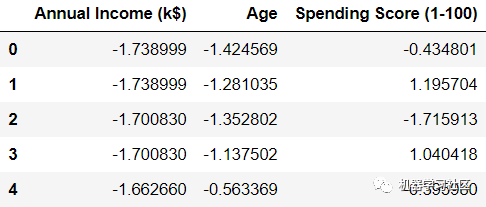我們可以看到所有的變量都被轉(zhuǎn)換了，現(xiàn)在都以零為中心。
熱編碼
變量"gender"是分類變量，我們需要把它轉(zhuǎn)換成一個數(shù)值變量，可以用pd.get_dummies()來處理。
gender = df['Gender']
newdf = scaled_features.join(gender)
newdf = pd.get_dummies(newdf, prefix=None, prefix_sep='_', dummy_na=False, columns=None, sparse=False, drop_first=False, dtype=None)
newdf = newdf.drop(['Gender_Male'],axis=1)
newdf.head()
讓我們再看一下數(shù)據(jù)：
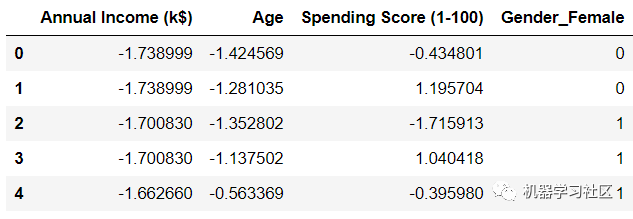
我們可以看到，性別變量已經(jīng)發(fā)生了變化，從數(shù)據(jù)框中刪除了“Gender_Male”。這是因為不需要再保留變量了。
建立聚類模型
讓我們構(gòu)建一個 K-means 聚類模型，并將其擬合到數(shù)據(jù)集中的所有變量上，我們用肘部圖可視化聚類模型的性能，它會告訴我們在構(gòu)建模型時使用的「最佳聚類數(shù)」。
SSE = []
for cluster in range(1,10):
kmeans = KMeans(n_jobs = -1, n_clusters = cluster, init='k-means++')
kmeans.fit(newdf)
SSE.append(kmeans.inertia_)
# converting the results into a dataframe and plotting them
frame = pd.DataFrame({'Cluster':range(1,10), 'SSE':SSE})
plt.figure(figsize=(12,6))
plt.plot(frame['Cluster'], frame['SSE'], marker='o')
plt.xlabel('Number of clusters')
plt.ylabel('Inertia')
可視化模型的性能：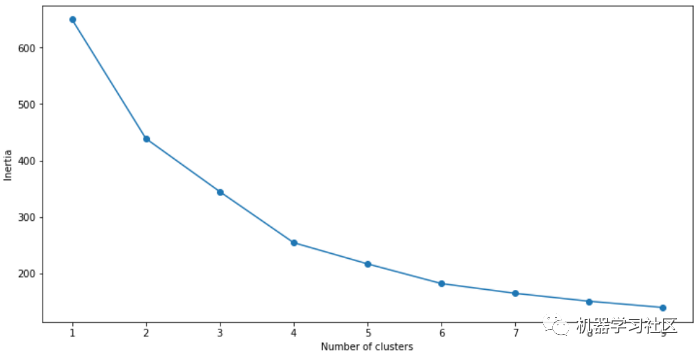
根據(jù)上面的肘部圖，我們可以看到最佳聚類數(shù)為「4」。
輪廓系數(shù)
輪廓系數(shù)或輪廓分?jǐn)?shù)是用于評估該算法創(chuàng)建的簇的質(zhì)量的方法。輪廓分?jǐn)?shù)在-1到+1之間。輪廓分?jǐn)?shù)越高，模型越好。輪廓分?jǐn)?shù)度量同一簇中所有數(shù)據(jù)點之間的距離。這個距離越小，輪廓分?jǐn)?shù)就越好。
讓我們計算一下我們剛剛建立的模型的輪廓分?jǐn)?shù)：
# First, build a model with 4 clusters
kmeans = KMeans(n_jobs = -1, n_clusters = 4, init='k-means++')
kmeans.fit(newdf)
# Now, print the silhouette score of this model
print(silhouette_score(newdf, kmeans.labels_, metric='euclidean'))
輪廓線得分約為「0.35」。這是一個不錯的模型，但我們可以做得更好，并嘗試獲得更高的簇群分離。
在我們嘗試這樣做之前，讓我們將剛剛構(gòu)建的聚類可視化，以了解模型的運(yùn)行情況：
clusters = kmeans.fit_predict(df.iloc[:,1:])
newdf["label"] = clusters
fig = plt.figure(figsize=(21,10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(newdf.Age[newdf.label == 0], newdf["Annual Income (k$)"][newdf.label == 0], df["Spending Score (1-100)"][newdf.label == 0], c='blue', s=60)
ax.scatter(newdf.Age[df.label == 1], newdf["Annual Income (k$)"][newdf.label == 1], newdf["Spending Score (1-100)"][newdf.label == 1], c='red', s=60)
ax.scatter(newdf.Age[df.label == 2], newdf["Annual Income (k$)"][newdf.label == 2], df["Spending Score (1-100)"][newdf.label == 2], c='green', s=60)
ax.scatter(newdf.Age[newdf.label == 3], newdf["Annual Income (k$)"][newdf.label == 3], newdf["Spending Score (1-100)"][newdf.label == 3], c='orange', s=60)
ax.view_init(30, 185)
plt.show()
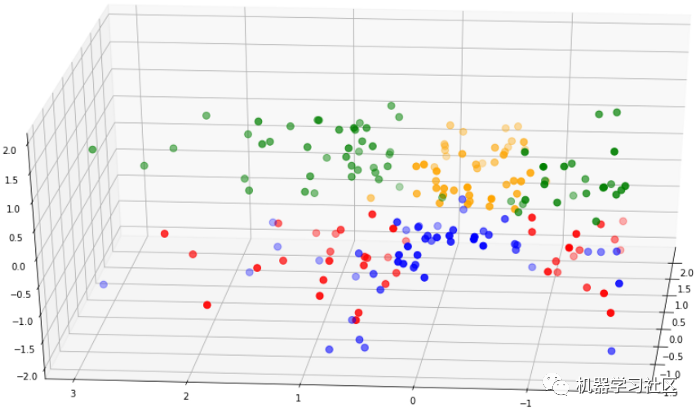
從上圖可以看出，簇類分離度不是很大。紅點與藍(lán)色混合，綠色與黃色重疊，這與輪廓分?jǐn)?shù)一起向我們表明該模型表現(xiàn)不佳。現(xiàn)在，讓我們創(chuàng)建一個比這個模型具有更好集群可分離性的新模型。
建立聚類模型2
對于這個模型，讓我們做一些特征選擇。我們可以使用一種叫做主成分分析（PCA）的技術(shù)。
PCA 是一種幫助我們降低數(shù)據(jù)集維數(shù)的技術(shù)。現(xiàn)在，讓我們在數(shù)據(jù)集上運(yùn)行PCA：
pca = PCA(n_components=4)
principalComponents = pca.fit_transform(newdf)
features = range(pca.n_components_)
plt.bar(features, pca.explained_variance_ratio_, color='black')
plt.xlabel('PCA features')
plt.ylabel('variance %')
plt.xticks(features)
PCA_components = pd.DataFrame(principalComponents)
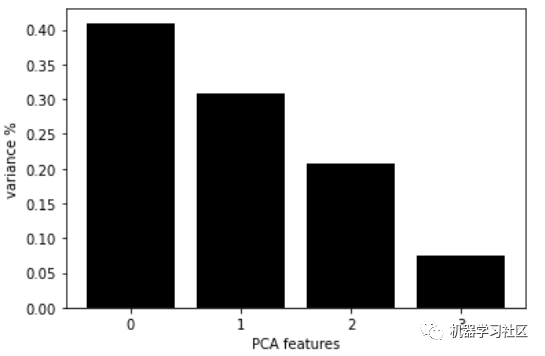這張圖表顯示了每個主成分分析的組成，以及它的方差。我們可以看到前兩個主成分解釋了大約70%的數(shù)據(jù)集方差。我們可以將這兩個組件輸入到模型中再次構(gòu)建模型，并選擇要使用的簇的數(shù)量
ks = range(1, 10)
inertias = []
for k in ks:
model = KMeans(n_clusters=k)
model.fit(PCA_components.iloc[:,:2])
inertias.append(model.inertia_)
plt.plot(ks, inertias, '-o', color='black')
plt.xlabel('number of clusters, k')
plt.ylabel('inertia')
plt.xticks(ks)
plt.show()
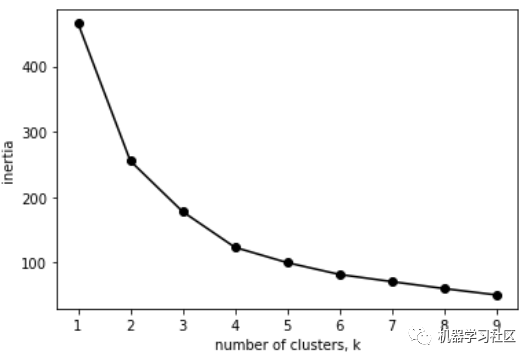同樣，看起來「最佳簇數(shù)是4」。我們可以用4個簇來計算此模型的輪廓分?jǐn)?shù)：
model = KMeans(n_clusters=4)
model.fit(PCA_components.iloc[:,:2])
# silhouette score
print(silhouette_score(PCA_components.iloc[:,:2], model.labels_, metric='euclidean'))
這個模型的輪廓分?jǐn)?shù)是「0.42」，這比我們之前創(chuàng)建的模型要好。我們可以像前面一樣可視化此模型：
model = KMeans(n_clusters=4)
clusters = model.fit_predict(PCA_components.iloc[:,:2])
newdf["label"] = clusters
fig = plt.figure(figsize=(21,10))
ax = fig.add_subplot(111, projection='3d')
ax.scatter(newdf.Age[newdf.label == 0], newdf["Annual Income (k$)"][newdf.label == 0], newdf["Spending Score (1-100)"][newdf.label == 0], c='blue', s=60)
ax.scatter(newdf.Age[newdf.label == 1], newdf["Annual Income (k$)"][newdf.label == 1], newdf["Spending Score (1-100)"][newdf.label == 1], c='red', s=60)
ax.scatter(newdf.Age[newdf.label == 2], newdf["Annual Income (k$)"][newdf.label == 2], newdf["Spending Score (1-100)"][newdf.label == 2], c='green', s=60)
ax.scatter(newdf.Age[newdf.label == 3], newdf["Annual Income (k$)"][newdf.label == 3], newdf["Spending Score (1-100)"][newdf.label == 3], c='orange', s=60)
ax.view_init(30, 185)
plt.show()
模型1與模型2
讓我們比較一下這個模型和第一個模型的聚類可分性：
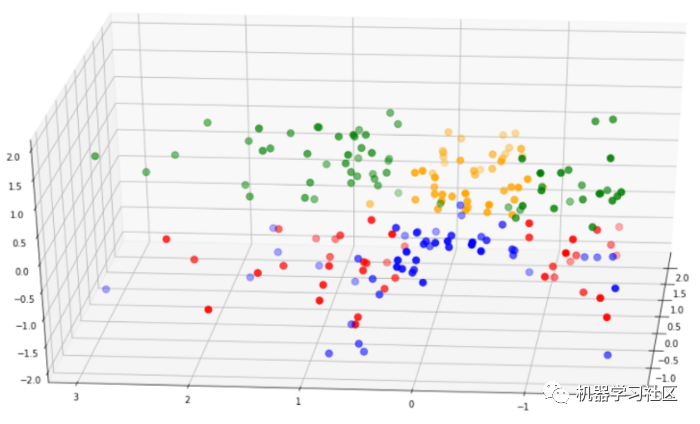
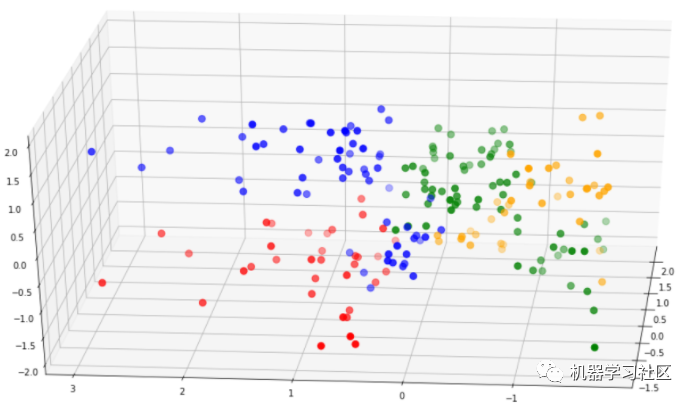第二個模型中的簇比第一個模型中的簇分離得好得多。此外，第二個模型的輪廓分?jǐn)?shù)要高得多。基于這些原因，我們可以選擇第二個模型進(jìn)行分析。
聚類分析
首先，讓我們將簇類映射回數(shù)據(jù)集，并查看數(shù)據(jù)幀。
df = pd.read_csv('Mall_Customers.csv')
df = df.drop(['CustomerID'],axis=1)
# map back clusters to dataframe
pred = model.predict(PCA_components.iloc[:,:2])
frame = pd.DataFrame(df)
frame['cluster'] = pred
frame.head()
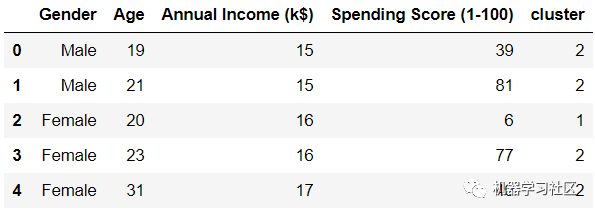數(shù)據(jù)幀中的每一行現(xiàn)在都分配給一個集群。要比較不同群集的屬性，請查找每個群集上所有變量的平均值：
avg_df = df.groupby(['cluster'], as_index=False).mean()
avg_df.show()
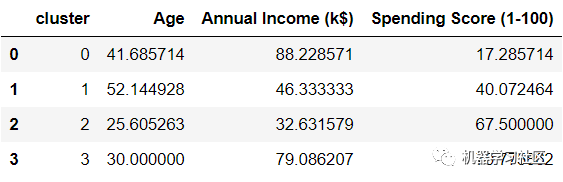如果我們將這些簇可視化，我們可以更容易地解釋它們。運(yùn)行以下代碼以獲得每個變量的不同可視化效果：
sns.barplot(x='cluster',y='Age',data=avg_df)
sns.barplot(x='cluster',y='Spending Score (1-100)',data=avg_df)
sns.barplot(x='cluster',y='Annual Income (k$)',data=avg_df)
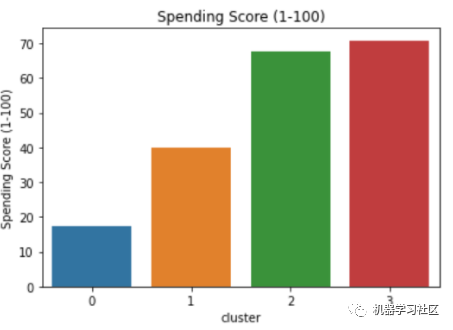
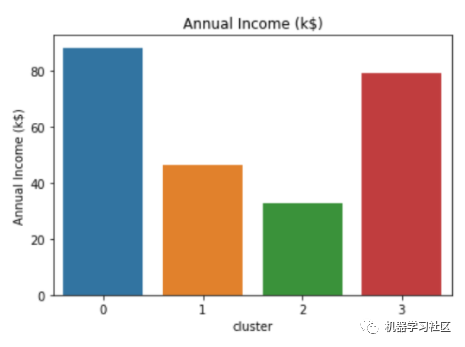
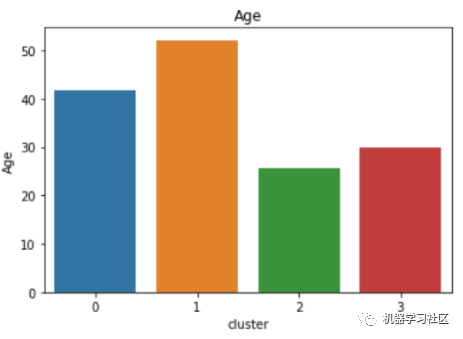
性別分類
df2 = pd.DataFrame(df.groupby(['cluster','Gender'])['Gender'].count())
df2.head()
各細(xì)分市場的主要特點
簇類0:
年平均收入高，支出低。 平均年齡在40歲左右，性別以男性為主。
簇類1：
中低收入，平均消費(fèi)能力。 平均年齡在50歲左右，性別以女性為主。
簇類2：
平均收入低，消費(fèi)分?jǐn)?shù)高。 平均年齡在25歲左右，性別以女性為主。
簇類3：
平均收入高，消費(fèi)分?jǐn)?shù)高。 平均年齡在30歲左右，性別以女性為主。
值得注意的是，計算年齡中位數(shù)將有助于更好地了解每個集群內(nèi)的年齡分布。
而且，女性在整個數(shù)據(jù)集中的代表性更高，這就是為什么大多數(shù)集群中女性的數(shù)量比男性多。我們可以找到每個性別相對于整個數(shù)據(jù)集中的數(shù)字的百分比，以便更好地了解性別分布。
為每個簇類構(gòu)建角色
作為一名數(shù)據(jù)科學(xué)家，能夠用你的分析講述一個故事是一項重要的技能，這將幫助你的客戶或利益相關(guān)者更容易理解你的發(fā)現(xiàn)。下面是一個基于創(chuàng)建的簇類構(gòu)建消費(fèi)者角色的示例：
簇類0
這個角色由對金錢非常謹(jǐn)慎的中年人組成。盡管與所有其他群體中的個人相比，他們的平均收入最高，但花費(fèi)最少。這可能是因為他們有經(jīng)濟(jì)責(zé)任——比如為孩子的高等教育存錢。
建議：促銷、優(yōu)惠券和折扣代碼將吸引這一領(lǐng)域的個人，因為他們傾向于少花錢。
簇類1
這部分人包括一個年齡較大的群體。他們掙的少，花的少，而且可能正在為退休儲蓄。
建議：針對這些人的營銷可以向這一領(lǐng)域的人推廣醫(yī)療保健相關(guān)產(chǎn)品。
簇類2
這一部分由較年輕的年齡組組成。這部分人最有可能是第一批求職者。與其他人相比，他們賺的錢最少。然而，這些人都是熱情的年輕人，他們喜歡過上好的生活方式，而且往往超支消費(fèi)。
建議：由于這些年輕人花費(fèi)很多，給他們提供旅游優(yōu)惠券或酒店折扣可能是個好主意。為他們提供折扣的頂級服裝和化妝品品牌也將很好地為這一部分。
簇類2
這部分人是由中年人組成的。這些人努力工作，積累了大量財富。他們也花大量的錢來過好的生活。
建議：由于他們的消費(fèi)能力和人口結(jié)構(gòu)，這些人很可能會尋找房產(chǎn)購買或投資。
結(jié)論
在本文中，我已經(jīng)詳細(xì)的建立了一個用于客戶細(xì)分的 K-Means 聚類模型。我們還探討了聚類分析，并分析了每個聚類中個體的行為。最后，我們看了一些可以根據(jù)集群中每個人的屬性提供的業(yè)務(wù)建議。
感謝你的分享，點贊，在看三連 