驚嘆！世界上最漂亮的排序算法！

直奔主題，世界上“最漂亮”的排序算法，只有6行。

void stooge_sort(int arr[], int i, int j){

         if (arr[i]>arr[j]) swap(arr[i], arr[j]);

         if (i+1>=j) return;

 

         int k=(j-i+1)/3;

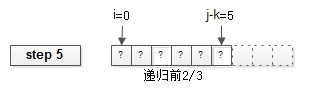
         stooge_sort(arr, i, j-k);

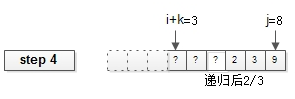
         stooge_sort(arr, i+k, j);

         stooge_sort(arr, i, j-k);

}

 

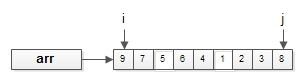
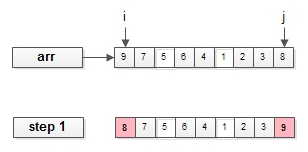
《算法導(dǎo)論》習(xí)題中的“完美排序”，由Howard、Fine等幾個(gè)教授提出，之所以稱為“完美排序”，是因?yàn)槠?strong>代碼實(shí)現(xiàn)，優(yōu)雅、工整、漂亮。

 

代碼不是很好理解，一步步講解下思路。

首先，排序傳入的參數(shù)是待排序的數(shù)組arr[i, j]；

 

第一步：比較i與j位置的元素，根據(jù)排序規(guī)則決定是否進(jìn)行置換。

畫外音：本栗子，假設(shè)排序規(guī)則是從小到大。

置換完成后，判斷排序是否結(jié)束，當(dāng)i和j相鄰時(shí)，排序結(jié)束。

 

第二步：將arr[i, j]三等分；

畫外音：總元素個(gè)數(shù)是j-i+1。

 

第三步：遞歸arr的前2/3半?yún)^(qū)。

 

第四步：遞歸arr的后2/3半?yún)^(qū)。

 

第五步：遞歸arr的前2/3半?yún)^(qū)。

 

排序結(jié)束。

 

神奇不神奇！！！

再看一遍，印象深刻不？

void stooge_sort(int arr[], int i, int j){

         if (arr[i]>arr[j]) swap(arr[i], arr[j]); // 比較

         if (i+1>=j) return; // 是否結(jié)束

 

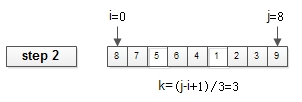
         int k=(j-i+1)/3; // 三等分

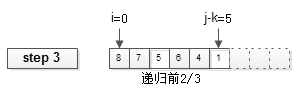
         stooge_sort(arr, i, j-k); // 前2/3半?yún)^(qū)

         stooge_sort(arr, i+k, j); // 后2/3半?yún)^(qū)

         stooge_sort(arr, i, j-k); // 前2/3半?yún)^(qū)

}

 

然并卵，除了代碼好看，完美排序毛用沒有，因?yàn)樗且粋€(gè)挺慢的算法。

 

由代碼很容易看出來：

（1）當(dāng)只有1個(gè)元素時(shí)，完美排序的時(shí)間也是1；

（2）當(dāng)有n個(gè)元素時(shí)，完美排序由一個(gè)常數(shù)計(jì)算，加上三次遞歸，每次遞歸數(shù)據(jù)量為(2/3)*n；

 

即，其時(shí)間復(fù)雜度遞歸式為：

T(1) = 1;

T(n) = 3T(2/3n) + 1;

 

通過遞歸式計(jì)算方法，最終得到，完美排序的時(shí)間復(fù)雜度是O(n^2.7)，比O(n^2)的排序都要慢。

 

完美排序的排序證明，不在文章中展開。從代碼直觀能感受到，通過swap和三次遞歸，趨勢上，小的元素會往前端走，大的元素會往后端走，直至完成排序。

畫外音：快速排序的過程是partition+兩次遞歸，也是小的元素往前端走，大的元素往后端走，直至完成排序。

希望這一分鐘，大家有收獲。

架構(gòu)師之路-分享可落地的技術(shù)文章

只有6行的完美排序，學(xué)到了嗎？

畫外音：今后面試手寫排序不再是問題。