排序算法第一篇-排序算法介紹

排序算法第一篇-排序算法介紹

在面試中，現(xiàn)在無論大小公司都會有算法的。其中排序算法也是一種很常見的面試題。比如冒泡，快排等。這些，排序算法自己看了一次又一次，可是過一段時間，又忘掉了。所以，這次就把算法是怎么推導(dǎo)出來的，詳細記錄下來。看看這次多久還會忘記。

本文主要介紹排序算法的分類、時間復(fù)雜度、空間復(fù)雜。為了后面的學習做準備的。

通過本文學習，將收獲到：排序算法分幾類？什么是算法的時間復(fù)雜度？是怎么算出來的？什么是算法的空間復(fù)雜度？常見的時間復(fù)雜度比較。

如果這些您都已經(jīng)知道了，可以不用耽誤時間看了。

約定：

文中的n2表示的是n的2次方(n2),n^2也是表示n的2次方；

n3表示的是n的3次方；

n^k表示的是n的k次方；

long2n表示的是以2為底的對數(shù)。

本文出自：凱哥Java(微信：kaigejava)學習Java版數(shù)據(jù)結(jié)構(gòu)與算法筆記。

一：介紹

排序又稱排序算法(Sort Algorithm),排序是將一組數(shù)據(jù)，依據(jù)指定的順序進行排序的過程。

二：分類

排序的分類分為兩大類

2.1：內(nèi)部排序

內(nèi)部排序是指將需要處理的所有數(shù)據(jù)一次性都加載到內(nèi)存中進行排序的。

如：冒泡、快排等這些算法都是內(nèi)部排序的

2.2：外部排序

數(shù)據(jù)量過大，無法全部加載到內(nèi)存中，需要借助于外部存儲進行排序的。

如：數(shù)據(jù)庫中數(shù)據(jù)8個G，內(nèi)存只有4個G的這種。

2.3：分類如下圖：

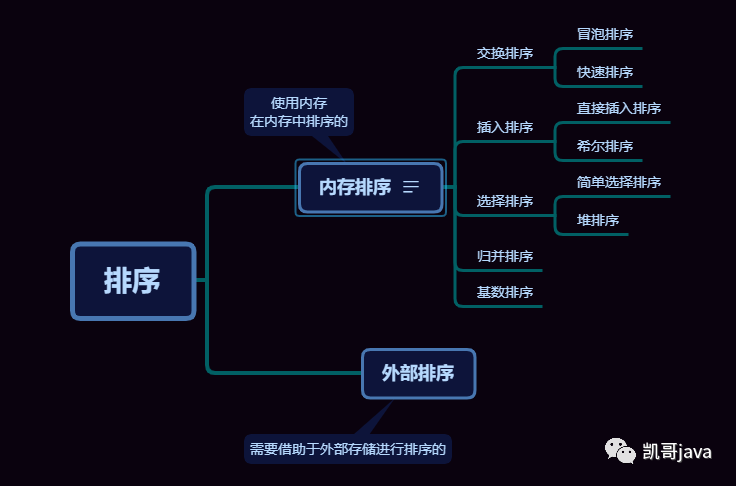
三：算法的時間復(fù)雜度

3.1：分類

衡量一個程序(算法)執(zhí)行時間有兩種方法

3.1.1：事后統(tǒng)計的方法

所謂的事后統(tǒng)計方法，顧名思義，就是程序(算法)已經(jīng)寫完了，運行后得到的結(jié)果。

這種方法雖然是可行的，但是有兩個問題：

①：要想對設(shè)計的算法運行的性能進行評估，需要實際運行該程序(浪費時間)；

②：運行所得的時間統(tǒng)計嚴重依賴于機器的硬件、軟件等環(huán)境因為。

這種方法有個嚴苛的要求：要在同一臺機器在相同狀態(tài)(軟硬件)下運行，才能比較哪個算法更快。

3.1.2：事前估算的方法

通過分析某個算法的時間復(fù)雜度來判斷哪個算法更優(yōu)。

3.2：時間頻度

概念：一個算法花費的時間與算法中語句執(zhí)行的次數(shù)成正比。哪個算法中語句執(zhí)行次數(shù)多，那么這個算法所花費的時間就多(這不廢話嗎)。

一個算法中語句執(zhí)行次數(shù)稱為語句頻度或時間頻度。記為：T(n).

(復(fù)雜的概念是，時間頻度：一個算法執(zhí)行所消耗的時間，從理論上是不能算出來的，想要具體數(shù)值，必須要將程序上機運行測試才能知道。但是我們不可能也沒必要對每個算法都上機進行測試的，只需要知道哪個算法花費的時間多，哪個算法花費的時間少就可以了。并且一個算法花費的時間與算法中語句執(zhí)行的次數(shù)成正比的，哪個算法中語句執(zhí)行次數(shù)多，那么這個程序花費的時間就多。一個算法中的語句執(zhí)行次數(shù)稱為語句頻度或者時間頻度，即為：T(n))

例如：我們知道的技術(shù)從1到100所有數(shù)字的和。這個就有兩種算法。分別如下：

①：使用for循環(huán)，從1到100循環(huán)出來，然后累加出來。代碼如下：

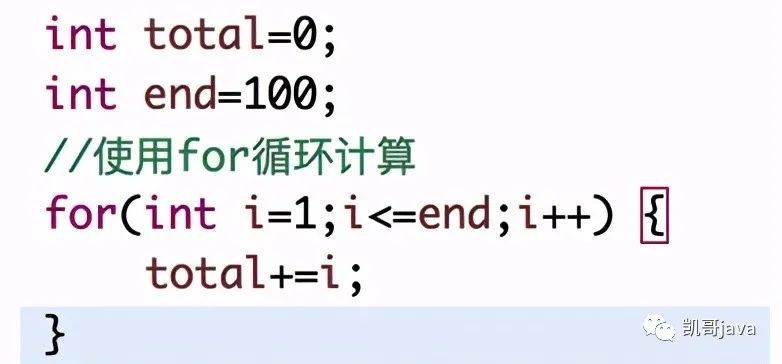
根據(jù)上面概念(注意對概念的理解,total和end這兩行相對于for循環(huán)來說，可以忽略。后面我們還會詳細講解還會忽略哪些)，我們來看下這個算法的時間頻度是多少呢？

在for循環(huán)中，實際需要執(zhí)行101次(+1的原因是因為，在for循環(huán)的時候，需要做最后一次判斷，才能推出。因此n個數(shù)的計算一共是n+1次操作)。所以其時間頻度就是：T(n)=n+1;

我們再來看看第二種算法：

是不是很簡單，只要一行代碼就執(zhí)行完成了。所以第二種算法的T(n)=1了。是不是很快呢？

時間頻度是不是一眼就看出來了？是不是不用在代碼運行下來比較運行時間了？

(ps：從上面簡單地從1到100求和算法中，我們是不是感受到算法的魅力了？感受到編程之美了？)

3.3：時間復(fù)雜度

在上面3.2中提到的時間頻度中,n稱為問題的規(guī)模，當n不斷變化的時候，時間頻度T(n)也會不斷變化。但是有時我們想知道它在變化的時候呈現(xiàn)什么樣的規(guī)律呢？為此，我們引入了時間復(fù)雜度概念。

一般情況下，算法中基本操作重復(fù)執(zhí)行的次數(shù)是問題規(guī)模n的某個函數(shù)，用T(n)表示。若有某個輔助函數(shù)f(n)，是的當n趨近于無窮大的時候，T(n)/f(n)的極限值為不等于零的參數(shù)，則稱為f(n)是T(n)的同數(shù)量級函數(shù)。記作T(n)=O(f(n)),稱O(f(n))為算法的漸進的時間復(fù)雜度。簡稱時間復(fù)雜度。這就是大O法。

在計算時間復(fù)雜度的時候，我們會忽略以下幾個數(shù)據(jù)值

3.3.1：忽略常數(shù)項

比如上面，我們計算1到100的第一種算法中，有兩行inttotal=0；和 int end = 100;這兩行代碼，這個數(shù)值是2，我們一般計算時間復(fù)雜度的時候，會忽略這個常數(shù)項的。為什么呢？請看下面四個函數(shù)，隨著n的增大而增大運行時間。

T(n) = 2n+20

T(n) = 2*n

T(n)=3n+10

T(n)=3*n

請看下圖隨著n的增大所呈現(xiàn)的規(guī)律：

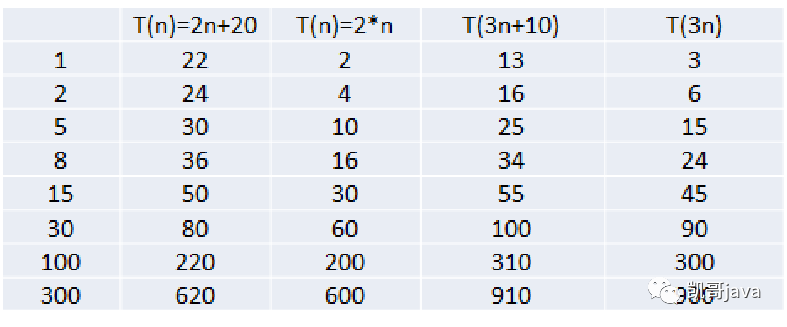
我們來看看，把這些數(shù)據(jù)使用折線圖展示：

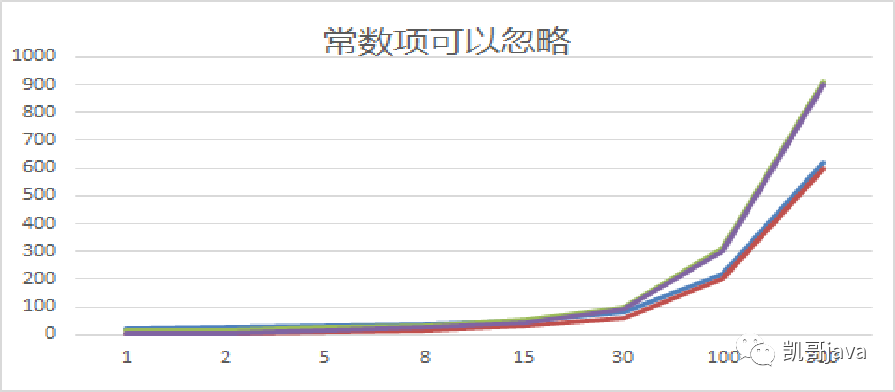
圖例說明：上面兩個是3*n及3n+10的，下面兩個是2n及2n+10的

從上面兩個圖表中我們可以得到以下結(jié)論：

①：2n+20和2*n隨著n的增加，執(zhí)行曲線無限接近(折線圖中下面兩個)，常量值20可以忽略了

②：3n+10和3*n隨著n的增加，執(zhí)行曲線無限接近(折線圖中上面兩個)，常量值10可以忽略了

所以，綜上所述，在計算程序(算法)時間復(fù)雜度的時候,常量值是可以忽略的

3.3.2：忽略低次項

請看下面四個函數(shù)，隨著n的增大又會呈現(xiàn)什么規(guī)律嗎？

T(n)=2n^2+3n+10

T(n)=2n^2

T(n)=n^2+5n+20

T(n)=n^2

說明：n^2表示n的2次方

我們來看看隨著n的增加，運行所消耗的時間。如下圖：

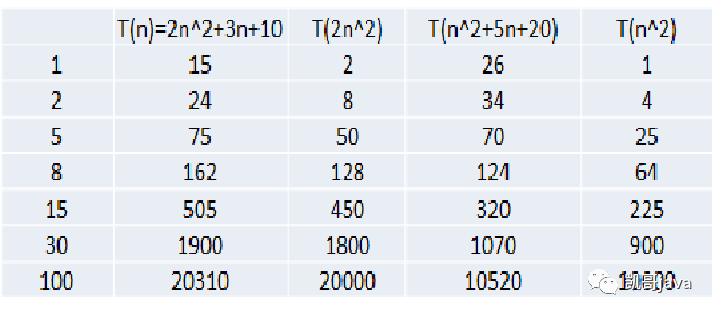
把上面數(shù)據(jù)，用折線圖表示，如下圖：

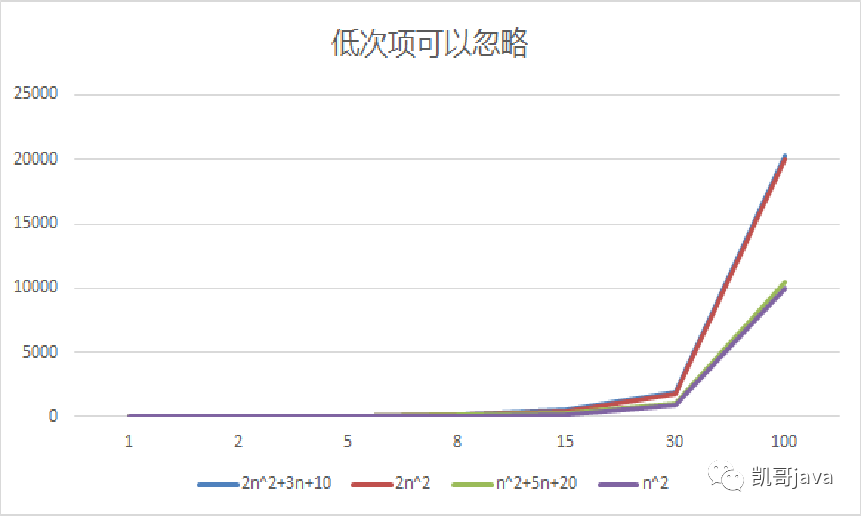
圖例說明：上面兩個是2n^2及2n^2+3n+10，下面兩個是n^2及 n^2+5n+20

從上面兩個圖中我們可以得到如下結(jié)論：

①：2n^2+3n+10和2n^2隨著n的增大，執(zhí)行曲線無限接近，可以忽略低次項及常量項：3n+10

②：n^2+5n+20和n^2隨著n的增大，執(zhí)行曲線無限接近，可以忽略低次項及常量項：5n+20

綜上所述，我們可以得到結(jié)論：在計算程序(算法)時間復(fù)雜度的時候，低次項(3n=3*n^1比n^2項數(shù)少)是可以忽略的

3.3.3：忽略系數(shù)

我們再來看看下面四個函數(shù)，看看它們隨著n的增大呈現(xiàn)出什么樣的規(guī)律

T(n)=3n^2+2n

T(n)=5n^2+7n

T(n)=n^3+5n

T(n)=6n^3+4n

隨著n的增加，運行時間所消耗耗時如下圖：

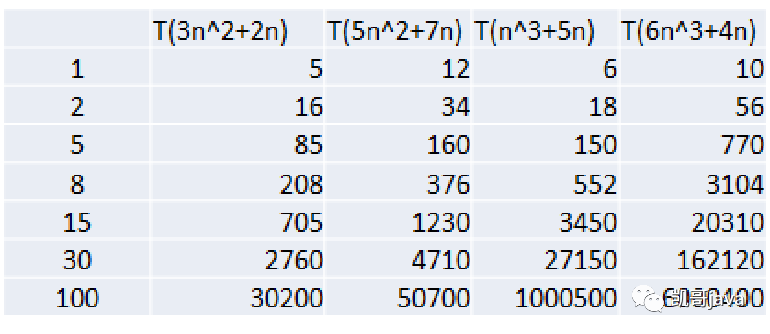
折線圖如下：

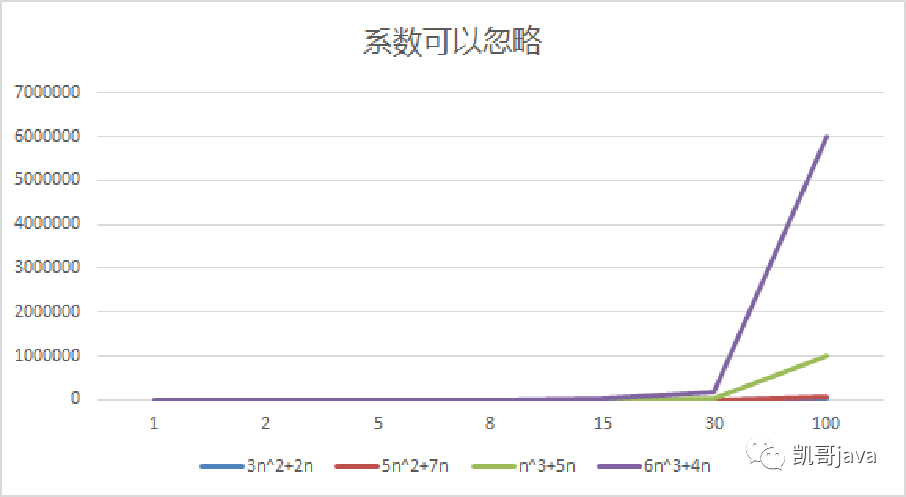
從上圖可以得到如下：

①：隨著n值變大，5n^2+7n和3n^2+2n，執(zhí)行曲線重合，說明這種情況下，系數(shù)5和3可以忽略；

②：n^3+5n和6n^3+4n，執(zhí)行曲線分離，說明多少次方是關(guān)鍵

3.3.4：總結(jié)：

• 計算時間復(fù)雜度的時候忽略常數(shù)項、忽略低次項、忽略系數(shù)

• T(n)不同，但時間復(fù)雜度可能相同。

如：T(n)=n2+7n+6與T(n)=3n^2+2n+2它們的T(n)不同，但時間復(fù)雜相同，都為O(n^2).

• 計算時間復(fù)雜度的方法用常數(shù)1代替運行時間中的所有加法常數(shù)T(n)=n^2+7n+6     =>T(n)=n^2+7n+1修改后的運行次數(shù)函數(shù)中，只保留最高階項T(n)=n^2+7n+1     => T（n）=n^2去除最高階項的系數(shù)T(n)=n^2 =>T(n)=n^2 => O(n^2)

3.4：常見的時間復(fù)雜度

• 常數(shù)階O(1)

• 對數(shù)階O(log2n)

• 線性階O(n)

• 線性對數(shù)階O(nlog2n)

• 平方階O(n^2)

• 立方階O(n^3)

• K次方階(n^k)

• 指數(shù)階O(2^n)

各個時間復(fù)雜度復(fù)雜度折線圖如下圖：

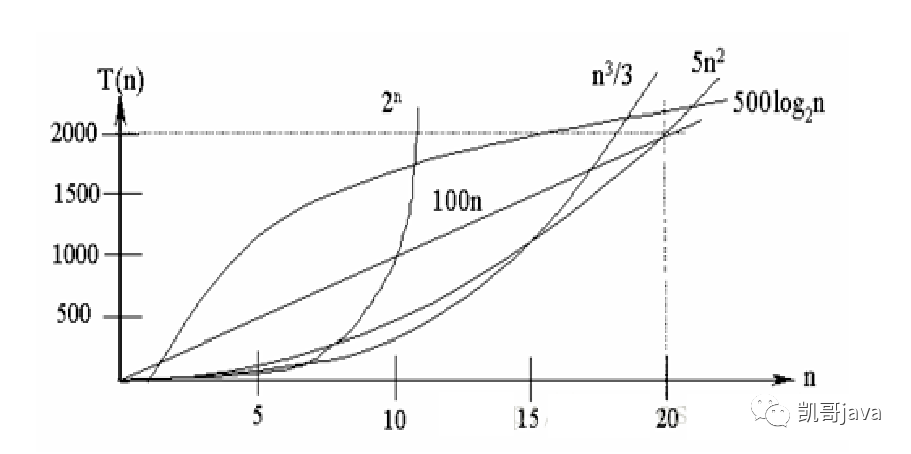
總結(jié)：

• 常見算法時間復(fù)雜度由小到大依次為：

O(1)<O(log2n)<O(n)<O(nlong2n)<O(n^2)<O(n^3)<O(n^K)<O（2^n）。隨著問題規(guī)模n的不斷增大，上述時間復(fù)雜度不斷增大,算法的執(zhí)行效率也越低；

• 從上圖折線圖中，我們可以看出，程序(算法)盡可能的避免使用指數(shù)階段的算法。

3.5：常見算法時間復(fù)雜度舉例

3.5.1：常數(shù)階O(1)

無論代碼執(zhí)行多少行，只要是沒有循環(huán)等復(fù)雜結(jié)構(gòu)，那這個代碼的時間復(fù)雜度就是O(1)

(計算時間復(fù)雜度的時候，忽略常數(shù)項)

代碼demo:

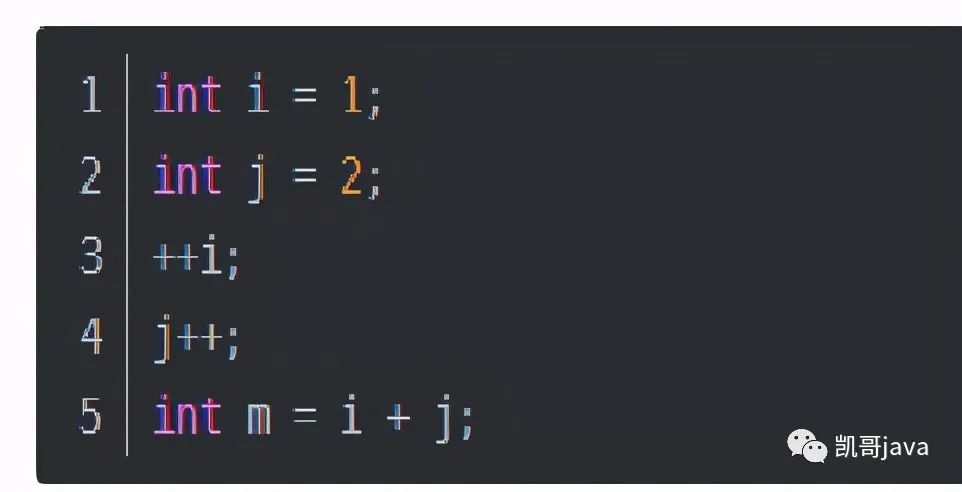
上述代碼在執(zhí)行的時候，消耗的時間并不是隨著某個變量的增長而增長，那么無論這類代碼有多長，即使有有幾萬幾十萬行，都是可以用O(1)來表示它的時間復(fù)雜度。

3.5.2：對數(shù)階O(log2n)

代碼敬上：

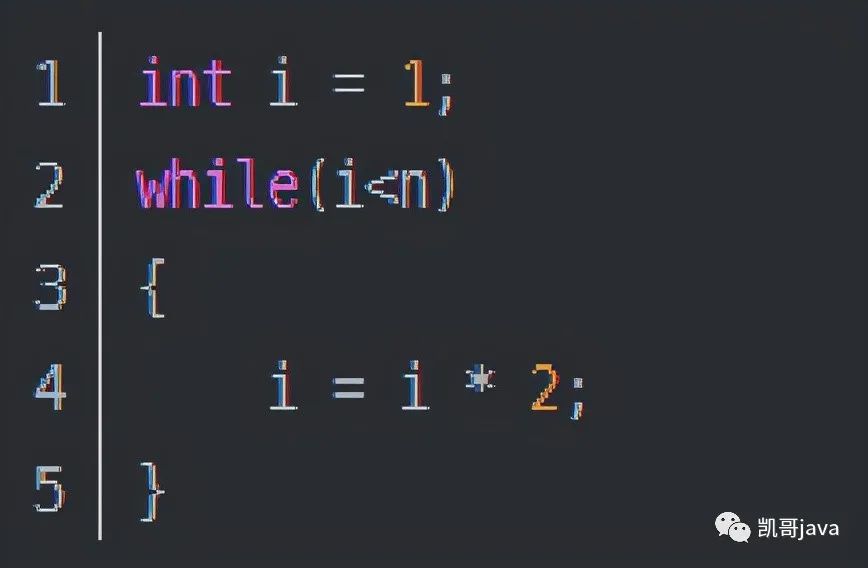
說明：

在while循環(huán)里面，每次都是將i*2的。n的值是固定的，所以在i乘完之后，i距離n就越來越近了。假設(shè)循環(huán)x次之后，i就大于n了，此時這個循環(huán)就退出了。也就是說2的x次方等于n了。那么x=log2n。也就是說當循環(huán)了log2n次以后，代碼就結(jié)束了。因此這個代碼的時間復(fù)雜度就是

O(log2n)。

O(log2n)的這個2時間上是隨著代碼變化的。如果i = i*3，那么時間復(fù)雜度就是O(log3n)

回顧下log的理解(這是初中知識點)：

如果a的x次方等于N（a>0,且a≠1），那么熟x就叫做以a為底的對數(shù)(logarithm)，記作x=logaN.

其中，a叫做對數(shù)的底數(shù)，N叫做真數(shù)，x叫做“以a為底N的對數(shù)”。

3.5.3：線性階O(n)

代碼如下：

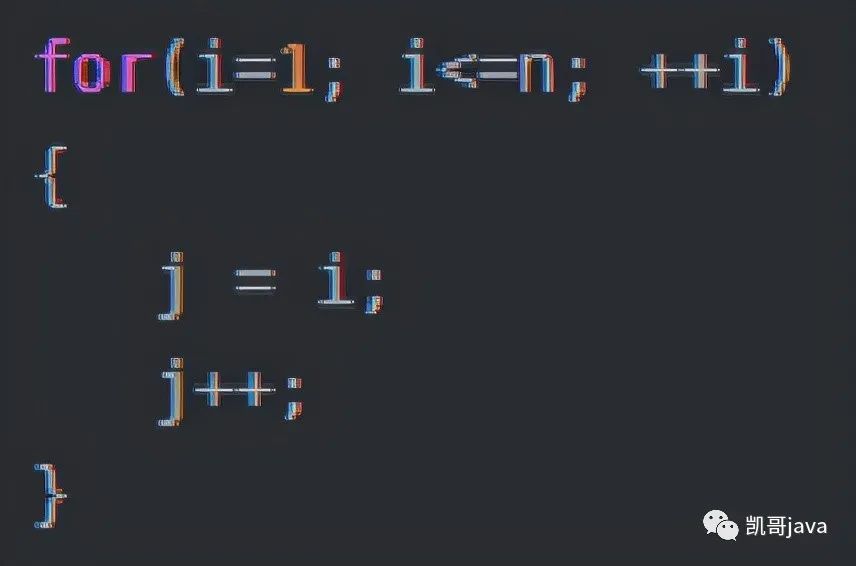
說明：

這段代碼，for循環(huán)里面的代碼會執(zhí)行n次。因此它所消耗的時間隨著n的變化而變化的，因此這類代碼都是可以用O(n)來表示它的時間復(fù)雜度。

3.5.4：線性對數(shù)階O(nlogn)

代碼如下：

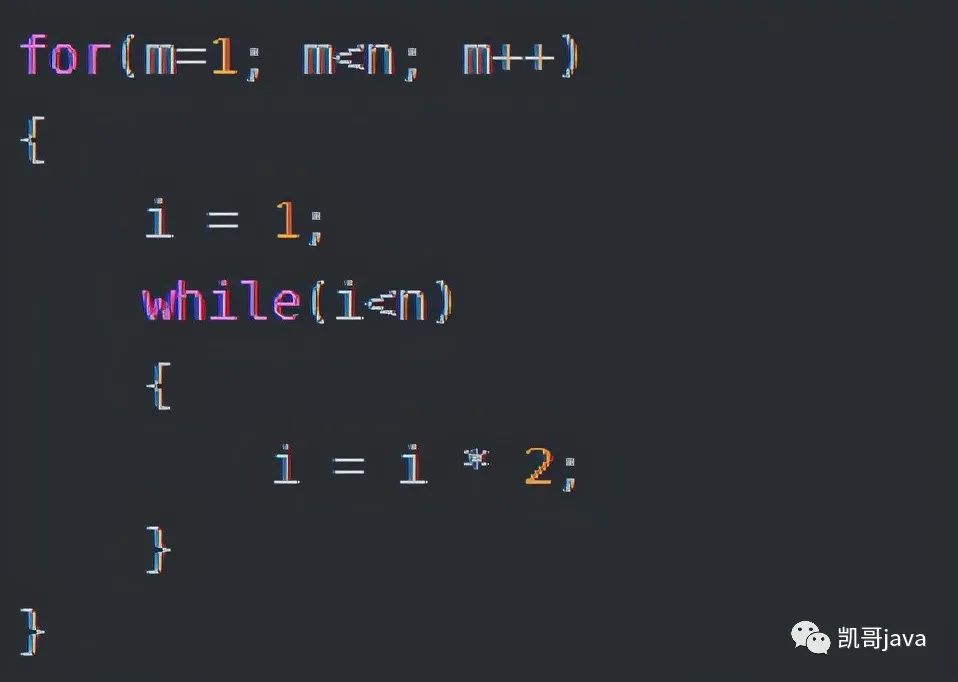
說明：

線性對數(shù)階O(nlogN)其實非常容易理解的。將時間復(fù)雜度為O(logn)的代碼循環(huán)了N次的話，那么它的時間復(fù)雜度就是n*O(logn)，也就是O(nlogN)

3.5.5：平方階O(n2)

代碼：

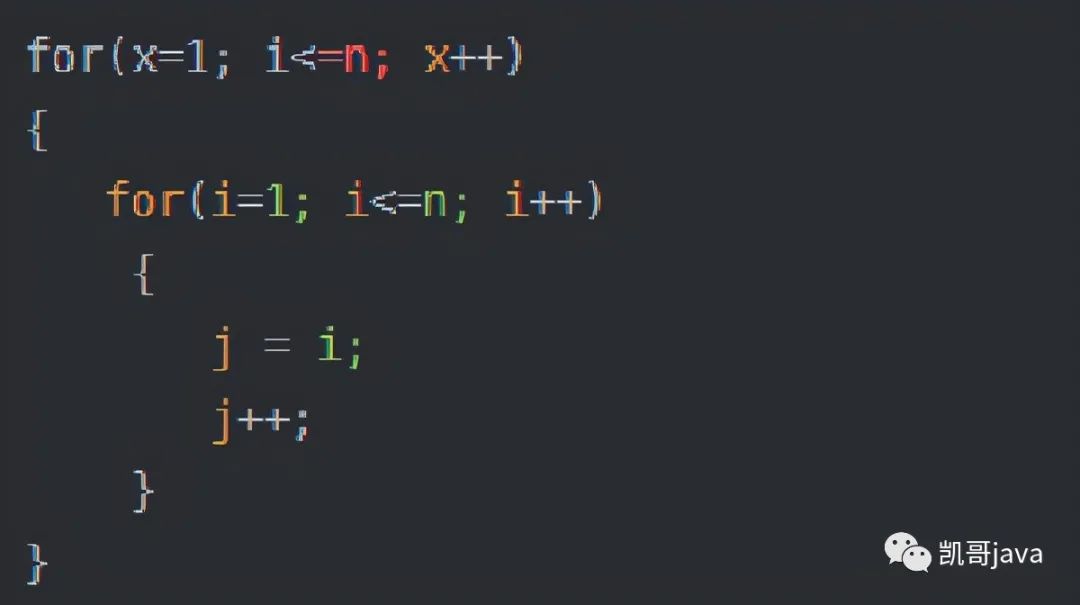
說明：

平方階O(n2)就容易理解了。如果把O(n)的代碼再嵌套循環(huán)一遍，它的時間復(fù)雜度就是O(n2)，

上圖中的代碼起始就是嵌套了2層n循環(huán)，它的時間復(fù)雜度就是O(n*n)，即時O(n2)。如果將其中一層循環(huán)的n修改成m，那么它的時間復(fù)雜度就變成了O(m*n).

3.5.6：立方階O(n3)、K次方階O(n^k)

說明：參考上面的O(n2)去理解就好了。O(n3)起始就相當于是三層n循環(huán)了。其他的一次類推。

3.6：平均時間復(fù)雜度和最壞時間復(fù)雜度

平均時間復(fù)雜度：

是指所有可能的輸入實例均以概率出現(xiàn)的情況下，該算法的運行時間

最壞時間復(fù)雜度：

是指在最壞情況下的時間復(fù)雜度稱為最壞時間復(fù)雜度。一般討論時間復(fù)雜度均是最壞情況下的時間復(fù)雜度。

這樣做的原因：最壞情況下的時間復(fù)雜度是算法在任何輸入實例上運行時間的界限。這就保證了算法的運行時間不會比最壞情況更長了。

平均時間復(fù)雜度和最壞時間復(fù)雜度是否一致，和算法有關(guān)。具體如下圖：

排序算法	平均時間	最壞情況	穩(wěn)定度	額外空間	備注
冒泡	O(n^2)	O(n^2)	穩(wěn)定	O(1)	n小的時候比較好
交換	O(n^2)	O(n^2)	不穩(wěn)定	O(1)	n小的時候比較好
選擇	O(n^2)	O(n^2)	不穩(wěn)定	O(1)	n小的時候比較好
插入	O(n^2)	O(n^2)	穩(wěn)定	O(1)	大部分已經(jīng)排序時比較好
基數(shù)	O(logRB)	O(logRB)	穩(wěn)定	O(n)	B是真書(0-9) R是基數(shù)(個十百)
Shell(希爾)	O(nlogn)	O(n^s) 1<s<2	不穩(wěn)定	O(1)	s是所選分組
快排	O(nlogn)	O(n^2)	不穩(wěn)定	O(nlogn)	n大時候較好
歸并	O(nlogn)	O(nlogn)	穩(wěn)定	O(1)	n大時候較好
堆	O(nlogn)	O(nlogn)	不穩(wěn)定	O(1)	n大時候較好

四：算法的空間復(fù)雜度

空間復(fù)雜度介紹

• 類似于時間復(fù)雜度的討論。一個算法的空間復(fù)雜度(Space Complexity)定義為該算法所消耗的存儲空間，它也是問題規(guī)模n的函數(shù)；

• 空間復(fù)雜度是對一個算法在運行過程中臨時占用存儲空間大小的量度。有的算法需要占用臨時工作單元數(shù)與解決問題的規(guī)模n有關(guān)。它們隨著n的增大而增大，當n較大的時候，將占用較多的存儲單元(存儲空間)。例如：在快排(快速排序)和歸并排序算法就屬于這種情況。

• 在做算法分析的時候，主要討論的是時間的復(fù)雜度。因為從用戶的使用體驗上來看，更看重的是程序執(zhí)行的速度的快慢。一般緩存產(chǎn)品(比如Redis)和技術(shù)排序算法本質(zhì)就是拿空間換時間的。

下節(jié)預(yù)告：

下節(jié)我們將講講冒泡排序和選擇排序。使用的是圖解+代碼一步一步推導(dǎo)出來演示的。歡迎大家一起學習。