如何從頻域的角度解釋CNN(卷積神經(jīng)網(wǎng)絡(luò))?
點擊上方“小白學(xué)視覺”,選擇加"星標(biāo)"或“置頂”
重磅干貨,第一時間送達
作者丨若羽
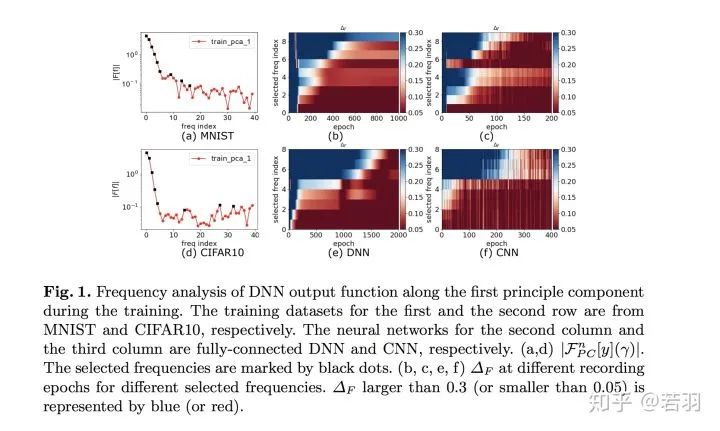
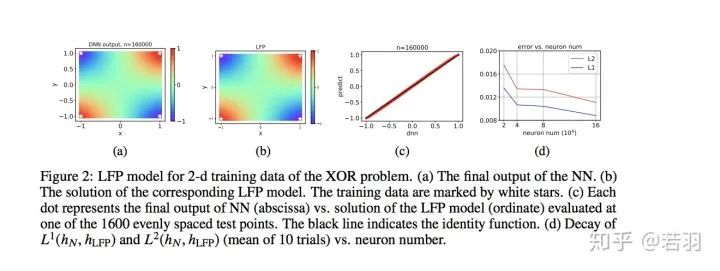
其次,與統(tǒng)計物理類似,LFP 模型只與網(wǎng)絡(luò)參數(shù)的一些宏觀統(tǒng)計量有關(guān),而與單個參數(shù)的具體行為無關(guān)。這種統(tǒng)計刻畫可以幫助我們準(zhǔn)確理解在參數(shù)極多的情況下 DNN 的學(xué)習(xí)過程,從而解釋 DNN 在參數(shù)遠(yuǎn)多于訓(xùn)練樣本數(shù)時較好的泛化能力。
在該工作中,我們通過一個等價的優(yōu)化問題來分析該 LFP 動力學(xué)的演化結(jié)果,并且給出了網(wǎng)絡(luò)泛化誤差的一個先驗估計。我們發(fā)現(xiàn)網(wǎng)絡(luò)的泛化誤差能夠被目標(biāo)函數(shù)f本身的一種 F-principle 范數(shù)(定義為?
 ?,γ(ξ) 是一個隨頻率衰減的權(quán)重函數(shù))所控制。
?,γ(ξ) 是一個隨頻率衰減的權(quán)重函數(shù))所控制。值得注意的是, 我們的誤差估計針對神經(jīng)網(wǎng)絡(luò)本身的學(xué)習(xí)過程,并不需要在損失函數(shù)中添加額外的正則項。關(guān)于該誤差估計我們將在之后的介紹文章中作進一步說明。


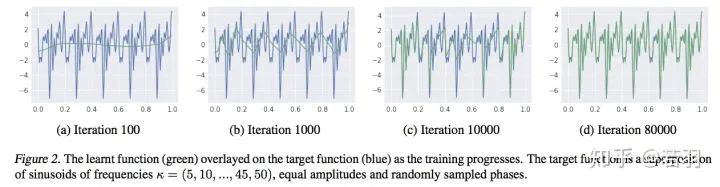
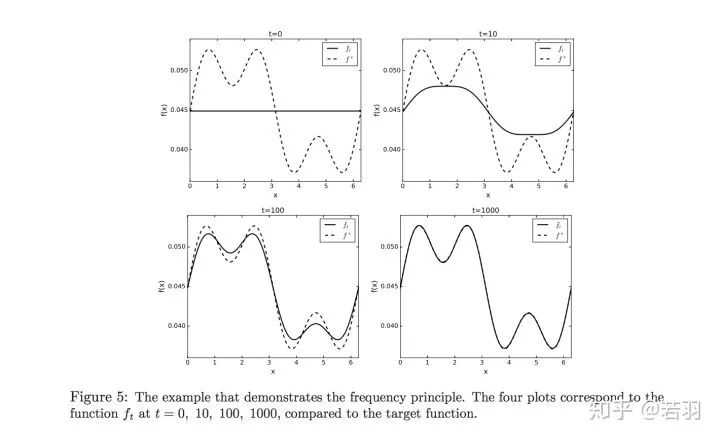
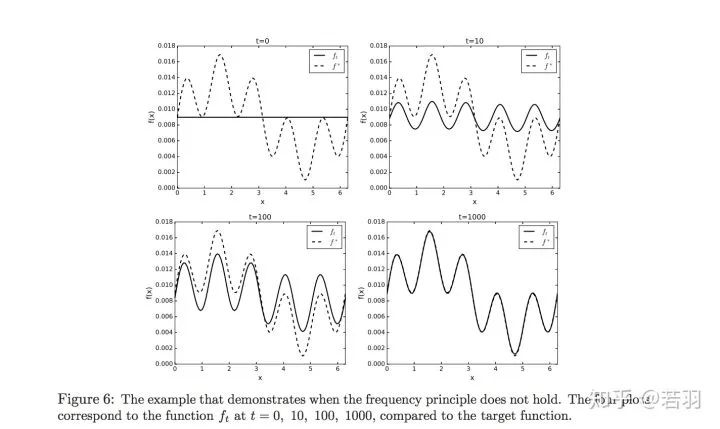
對函數(shù)做實驗: 
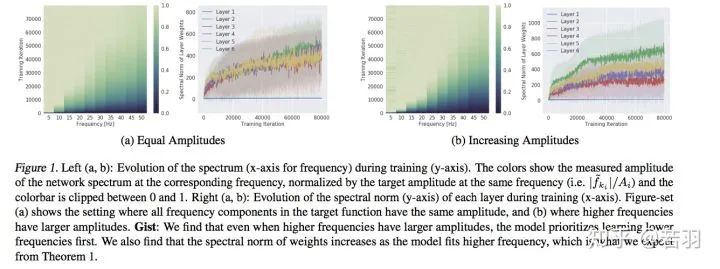


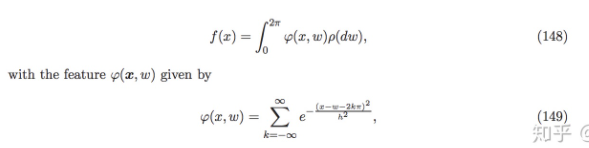
 ?概率測度
?概率測度






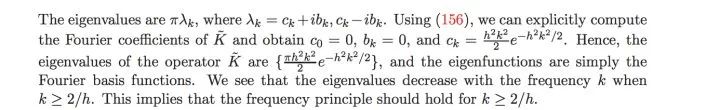
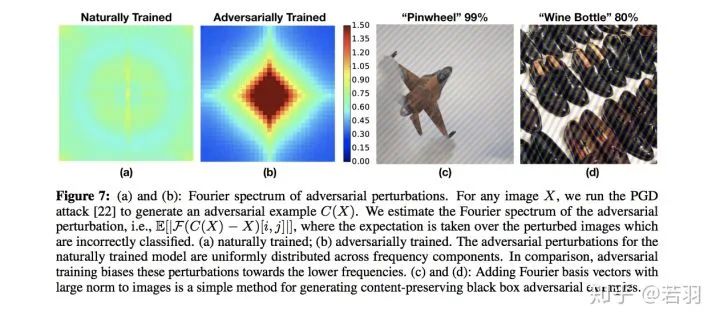
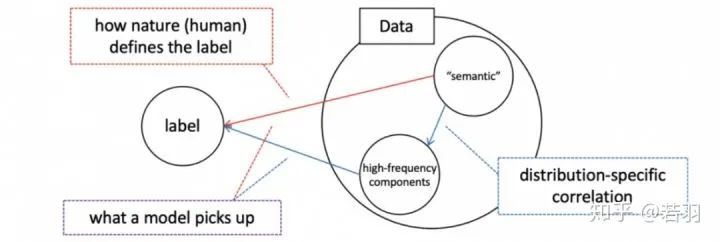

對于一個訓(xùn)練好的模型,我們調(diào)整其權(quán)重,使卷積核變得更加平滑;
直接在訓(xùn)練好的卷積核上將高頻信息過濾掉;
在訓(xùn)練卷積神經(jīng)網(wǎng)絡(luò)的過程中增加正則化,使得相鄰位置的權(quán)重更加接近。
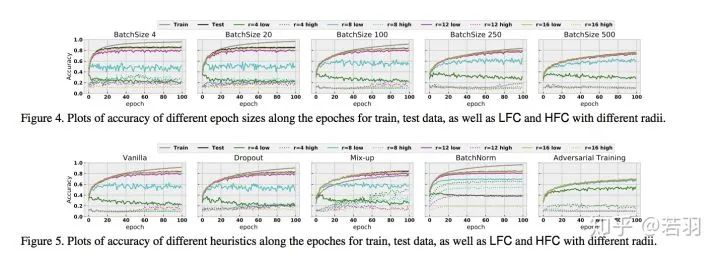
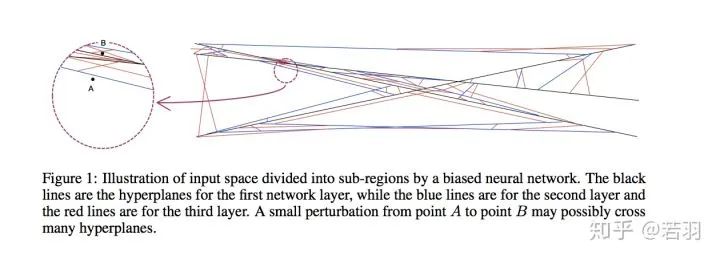


作者丨心似風(fēng)往
評論
圖片
表情
