囯产精品久久久久久久久久免费 ,在线激情小电影,黑人操亚洲比大片,日B视频在线观看,人妻少妇无码视频免费看,天天撸天天搞,日韩视频在线观看二区,色鸡鸡综合网

本文旨在介紹當前被大家廣為所知的超參自動優(yōu)化方法，像網格搜索、隨機搜索、貝葉斯優(yōu)化和Hyperband，并附有相關的樣例代碼供大家學習。

一、網格搜索(Grid Search)

網格搜索是暴力搜索，在給定超參搜索空間內，嘗試所有超參組合，最后搜索出最優(yōu)的超參組合。sklearn已實現(xiàn)該方法，使用樣例如下:

from sklearn import svm, datasetsfrom sklearn.model_selection import GridSearchCVimport pandas as pd
# 導入數(shù)據(jù)iris = datasets.load_iris()# 定義超參搜索空間parameters = {'kernel':('linear', 'rbf'), 'C':[1, 10]}# 初始化模型svc = svm.SVC()# 網格搜索clf = GridSearchCV(estimator = svc,                   param_grid = parameters,                   scoring = 'accuracy',                   n_jobs = -1,                   cv = 5)clf.fit(iris.data, iris.target)返回：GridSearchCV(cv=5, estimator=SVC(), n_jobs=-1,                   param_grid={'C': [1, 10], 'kernel': ('linear', 'rbf')},                   scoring='accuracy')
# 打印結果print('詳細結果:\n', pd.DataFrame.from_dict(clf.cv_results_))print('最佳分類器:\n', clf.best_estimator_)print('最佳分數(shù):\n', clf.best_score_)print('最佳參數(shù):\n', clf.best_params_).返回：詳細結果:    mean_fit_time  std_fit_time  mean_score_time  std_score_time param_C  ... split3_test_score split4_test_score  mean_test_score  std_test_score  rank_test_score0       0.000788      0.000394         0.000194        0.000389       1  ...          0.966667               1.0         0.980000        0.016330                11       0.000804      0.000402         0.000199        0.000399       1  ...          0.933333               1.0         0.966667        0.021082                42       0.000593      0.000484         0.000593        0.000484      10  ...          0.966667               1.0         0.973333        0.038873                33       0.000593      0.000484         0.000399        0.000489      10  ...          0.966667               1.0         0.980000        0.016330                1[4 rows x 15 columns]最佳分類器: SVC(C=1, kernel='linear')最佳分數(shù):0.9800000000000001最佳參數(shù): {'C': 1, 'kernel': 'linear'}

sklearn.model_selection.GridSearchCV[1]的重要參數(shù)說明:

estimator: scikit-learn模型。
param_grid: 超參搜索空間，即超參數(shù)字典。
scoring: 在交叉驗證中使用的評估策略。
n_jobs: 并行任務數(shù)，-1為使用所有CPU。
cv: 決定采用幾折交叉驗證。

二、隨機搜索(Randomized Search)

隨機搜索是在搜索空間中采樣出超參組合，然后選出采樣組合中最優(yōu)的超參組合。隨機搜索的好處如下圖所示：

圖1: 網格搜索和隨機搜索的對比[2]

解釋圖1，如果目前我們要搜索兩個參數(shù)，但參數(shù)A重要而另一個參數(shù)B并沒有想象中重要，網格搜索9個參數(shù)組合(A, B)，而由于模型更依賴于重要參數(shù)A，所以只有3個參數(shù)值是真正參與到最優(yōu)參數(shù)的搜索工作中。反觀隨機搜索，隨機采樣9種超參組合，在重要參數(shù)A上會有9個參數(shù)值參與到搜索工作中，所以，在某些參數(shù)對模型影響較小時，使用隨機搜索能讓我們有更多的探索空間。

同樣地，sklearn實現(xiàn)了隨機搜索[3]，樣例代碼如下:

from sklearn import svm, datasetsfrom sklearn.model_selection import RandomizedSearchCVimport pandas as pdfrom scipy.stats import uniform

# 導入數(shù)據(jù)iris = datasets.load_iris()# 定義超參搜索空間distributions = {'kernel':['linear', 'rbf'], 'C':uniform(loc=1, scale=9)}# 初始化模型svc = svm.SVC()# 網格搜索clf = RandomizedSearchCV(estimator = svc,                         param_distributions = distributions,                         n_iter = 4,                         scoring = 'accuracy',                         cv = 5,                         n_jobs = -1,                         random_state = 2021)clf.fit(iris.data, iris.target)返回：RandomizedSearchCV(cv=5, estimator=SVC(), n_iter=4, n_jobs=-1,                         param_distributions={'C': <scipy.stats._distn_infrastructure.rv_frozen object at 0x000001F372F9A190>,                                              'kernel': ['linear', 'rbf']},                         random_state=2021, scoring='accuracy')

# 打印結果print('詳細結果:\n', pd.DataFrame.from_dict(clf.cv_results_))print('最佳分類器:\n', clf.best_estimator_)print('最佳分數(shù):\n', clf.best_score_)print('最佳參數(shù):\n', clf.best_params_)返回：詳細結果:    mean_fit_time  std_fit_time  mean_score_time  std_score_time  param_C  ... split3_test_score split4_test_score  mean_test_score  std_test_score  rank_test_score0       0.000598      0.000489         0.000200        0.000400   6.4538  ...          0.966667               1.0         0.986667        0.016330                11       0.000997      0.000002         0.000000        0.000000  4.99782  ...          0.966667               1.0         0.980000        0.026667                32       0.000798      0.000399         0.000399        0.000488  3.81406  ...          0.966667               1.0         0.980000        0.016330                33       0.000598      0.000488         0.000200        0.000399  5.36286  ...          0.966667               1.0         0.986667        0.016330                1[4 rows x 15 columns]最佳分類器: SVC(C=6.453804509266643)最佳分數(shù):0.9866666666666667最佳參數(shù): {'C': 6.453804509266643, 'kernel': 'rbf'}

相比于網格搜索，sklearn隨機搜索中主要改變的參數(shù)是param_distributions，負責提供超參值分布范圍。

三、貝葉斯優(yōu)化(Bayesian Optimization)

我寫本文的目的主要是沖著貝葉斯優(yōu)化來的，一直有所耳聞卻未深入了解，所以我就來查漏補缺了。以下內容主要基于Duane Rich在《How does Bayesian optimization work?》[4]的回答。

調優(yōu)的目的是要找到一組最優(yōu)的超參組合，能使目標函數(shù)f達到全局最小值。

$x^{*}=\underset{x\in X}{argmin}f(x)$ 舉個例子，若學習率設置過大，模型可能會在代價函數(shù)的全局最優(yōu)點附近不斷來回震蕩，甚至跳出全局最優(yōu)點，而設置過小，又可能會陷入局部最優(yōu)，因此調學習率這一參數(shù)，是為了讓模型能收斂到代價函數(shù)的全局最小值。可是在機器學習中，目標函數(shù) $f$ 常是被稱作expensive blackbox function，計算開銷大且不一定為凸函數(shù)。為此，貝葉斯優(yōu)化出現(xiàn)了，它特別適合針對expensive blackbox function找到全局最優(yōu)。

假設我們的真實的目標函數(shù) $f(x)$ 長下圖這樣：

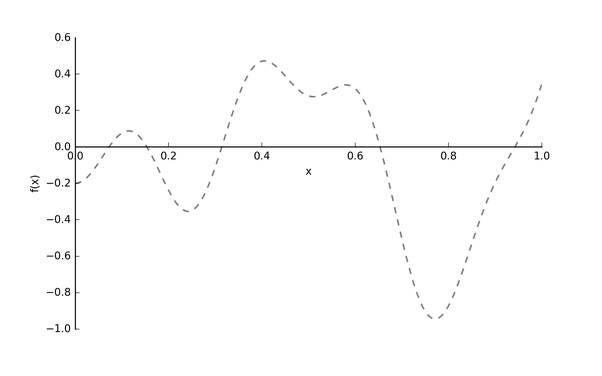
圖2: 目標函數(shù)f(x)[4]

注意: 目標函數(shù) $f(x)$ 的 $x$ 是指超參數(shù)，我們希望找到最優(yōu)的超參 $x$ 去得到最小的 $f(x)$ 。為什么用虛線表示 $f(x)$ 呢？因為它是黑箱函數(shù)(blackbox function)。

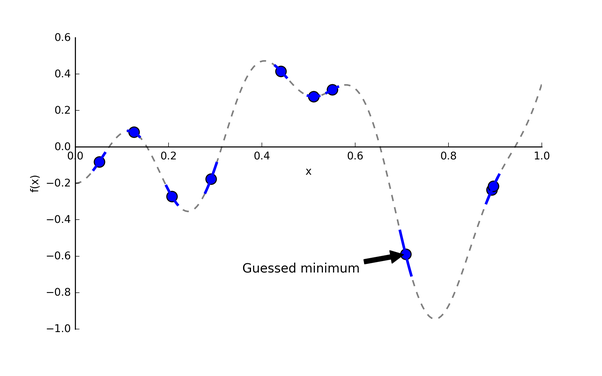
現(xiàn)在，我們怎么找到 $f(x)$ 全局最小值點呢？我們能不能先在 $f(x)$ 上隨機采樣10個點，然后取它們的最小值呢？

圖3: 隨機采樣10個點的目標函數(shù)f(x)[4]

圖3里確實有個點挺靠近全局最優(yōu)點的，那是不是在它附近再采樣幾個點，不斷重復就行了？沒那么簡單，萬一起始采樣點在局部最小值附近，那這種方法會很容易陷入局部最優(yōu)。關于“如何找到下一個合適的點”這個問題，我們先放一放，因為我們漏掉一個重點：每次嘗試一種超參值 $x$ ，計算 $f(x)$ 的代價是昂貴的，為了減輕開銷，貝葉斯優(yōu)化采用了代理模型(surrogate model)，代理模型可以被看作是一個簡單模型去擬合原本復雜且不好理解的模型，簡單來說，就是 $f(x)$ 計算太昂貴了，我們就用代理模型去代替它。

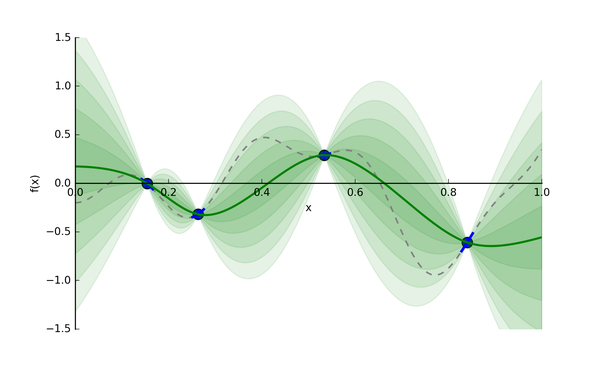
貝葉斯優(yōu)化使用了高斯過程(gasussian processes, GP)去構建代理模型，高斯過程的細節(jié)這里暫時不講，有興趣的小伙伴可以自行查閱資料了解。基于給定的輸入和輸出，GP會推斷出一個模型(這里為代理模型)。假設我們從昂貴的 $f(x)$ 采樣了4個點，然后我們把這4個點交給GP，它會返回一個代理模型，如下圖所示：

圖4: 目標函數(shù)f(x)和代理模型[4]

綠色實線就是GP猜的代理模型，綠色條帶是輸出分布的標準差(即為Uncertainty)。我們有了代理模型，后續(xù)我們去找下一個合適的超參值，就能帶入到計算開銷相對較小的代理模型中，評估給定超參值的情況。

現(xiàn)在，我們來思考回之前提到的問題:"如何找到下一個合適的點?"，這個問題本質是在問:“哪里有全局最小的點？”，為了解決這個問題，我們要關注兩個地方:

(1) 已開發(fā)區(qū)域: 在綠色實線上最低的超參點。因為很可能它附近存在全局最優(yōu)點。

(2) 未探索區(qū)域: 綠色實線上還未被探索的區(qū)域。比如圖4，相比于0.15-0.25區(qū)間，0.65-0.75區(qū)間更具有探索價值(即該區(qū)間Uncertainty更大)。探索該區(qū)域有利于減少我們猜測的方差。

為了實現(xiàn)以上探索和開發(fā)的平衡(exploration-exploitation trade-off)，貝葉斯優(yōu)化使用了采集函數(shù)(acquisition function)，它能平衡好全局最小值的探索和開發(fā)。采集函數(shù)有很多選擇，其中最常見的是expectated of improvement(EI)[5]，我們先看一個utility function:

$u(x)=max(0,f^{'}-f(x))$ $f^{'}$ 是目前觀察到的最小值， $x$ 是超參值，我們希望上述utility function輸出越大越好(即找到的 $x$ 能獲得比當前最小值還小)，基于 $u(x)$ ，EI采集函數(shù)如下所示:

$\begin{aligned}a_{EI}(x)&=\mathbb{E}[u(x)|x,D]\\&=\int_{-\infty }^{f^{'}}(f^{'}-f)N(f;\mu(x),K(x,x))df\\&=(f^{'}-\mu(x))\phi (f^{'}-f)N(f^{'};\mu(x),K(x,x))+K(x,x)N(f^{'};\mu(x),K(x,x))\end{aligned}$

具有最高的EI的超參值 $x$ 會被選擇。EI有兩部分：

(1) 減少均值函數(shù) $\mu(x)$ ，提高EI。

(2) 增加方差 $K(x, x)$ ，提高EI。

所以EI的提高是建立在均值和方差的trade-off，也是exploration和exploitation的trade-off。

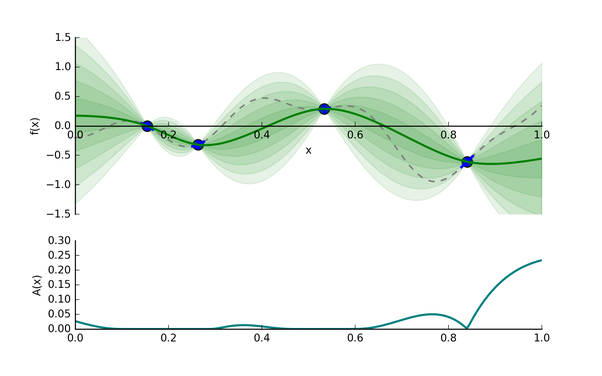
圖5: 采集函數(shù)A(x)

圖5我們可以看到， $x=1$ 時EI最大，所以我們下一個超參值 $x$ 應該選1。

講到這里，我們來看下完整的貝葉斯優(yōu)化步驟是怎樣的：

圖6: 貝葉斯優(yōu)化-SMBO

SMBO是簡潔版的貝葉斯優(yōu)化，偽代碼如圖6所示，具體如下：

(1) 準備輸入: expensive blackbox function $f$ ，超參搜索空間 $X$ ，采樣數(shù)據(jù)集 $D$ (超參組合 $x$ ，對應 $f(x)$ 輸出值)，采集函數(shù) $S$ 和用數(shù)據(jù)集 $D$ 擬合的代理模型M。

(2) 基于 $X$ 和 $f$ ，采樣得到數(shù)據(jù)集 $D={(x_1, y_1), ..., (x_i, y_i)}$ 。

(3) 循環(huán)選 $T$ 次參數(shù)：

用當前數(shù)據(jù)集 $D$ 擬合代理模型 $M$ ，實現(xiàn)模型更新。
選擇使采集函數(shù) $S$ 最大的超參組合 $x$ 。
將 $x$ 帶入 $f$ 中，得到輸出值 $y$ 。(注意這里 $f$ 的計算開銷大)
將新的 $(x, y)$ 加入到現(xiàn)有數(shù)據(jù)集 $D$ 中。

目前，Hyperopt[6]開源代碼庫已實現(xiàn)基于TPE(Tree-structured Parzen Estimator Approach)的貝葉斯優(yōu)化，圖6我們能看到GP構建的概率模型是 $p(y|x)$ ，而TPE是 $p(x|y)$ 和 $p(y)$ ，關于TPE和GP的對比討論，建議閱讀論文[7]。TPE樣例代碼如下：

from sklearn import svm, datasetsfrom sklearn.model_selection import cross_val_scorefrom hyperopt import hp, fmin, tpe, space_evalimport pandas as pd
# 導入數(shù)據(jù)iris = datasets.load_iris()
# step1: 定義目標函數(shù)def objective(params):      # 初始化模型并交叉驗證      svc = svm.SVC(**params)      cv_scores = cross_val_score(svc, iris.data, iris.target, cv=5)      # 返回loss = 1 - accuracy (loss必須被最小化)      loss = 1 - cv_scores.mean()      return loss
# step2: 定義超參搜索空間space = {'kernel':hp.choice('kernel', ['linear', 'rbf']),         'C':hp.uniform('C', 1, 10)}
# step3: 在給定超參搜索空間下，最小化目標函數(shù)best = fmin(objective, space, algo=tpe.suggest, max_evals=100)返回: best_loss: 0.013333333333333308(即accuracy為0.9866666666666667)
# step4: 打印結果print(best)返回:{'C': 6.136181888987526, 'kernel': 1}(PS:kernel為0-based index,這里1指rbf)

四、Hyperband

除了格子搜索、隨機搜索和貝葉斯優(yōu)化，還有其它自動調參方式。例如Hyperband optimization[8]，Hyperband本質上是隨機搜索的一種變種，它使用早停策略和Sccessive Halving算法去分配資源，結果是Hyperband能評估更多的超參組合，同時在給定的資源預算下，比貝葉斯方法收斂更快，下圖展示了Hyperband的早停和資源分配:

圖7: Hyperband的超參選擇和評估

在Hyperband之后，還出現(xiàn)了BOHB，它混合了貝葉斯優(yōu)化和Hyperband。Hyperband和BOHB的開源代碼可參考HpBandSter庫[9]，這里不展開細講。

五、總結

上面我們用Iris鳶尾花數(shù)據(jù)集試了不同的超參自動調優(yōu)方法，發(fā)現(xiàn)貝葉斯優(yōu)化和隨機搜索都比格子搜索好。從一些論文反映，貝葉斯優(yōu)化是更香的，但是貝葉斯優(yōu)化好像在實踐中用的不是那么多，網上也有很多分享者，像Nagesh Singh Chauhan，說的那樣：

As a general rule of thumb, any time you want to optimize tuning hyperparameters, think Grid Search and Randomized Search! [10]
Hyperparameter Optimization for Machine Learning Models - Nagesh Singh Chauhan

為什么呢？我想原因是貝葉斯的開銷太大了，前面有提到，在每次循環(huán)選超參值的時候，貝葉斯優(yōu)化都需要將 $x$ 帶入昂貴的目標函數(shù) $f$ 中，去得到輸出值y，當目標函數(shù)特別復雜時，這種情況的評估開銷是很大的，更何況隨著搜索空間和搜索次數(shù)的變大，計算會越發(fā)昂貴。在知乎《為什么基于貝葉斯優(yōu)化的自動調參沒有大范圍使用？》[11]中，很多知乎主也給出了很認真的回復，建議有興趣的朋友移步閱讀。

寫這篇文章的過程中，我主要學到了2點，一是隨機搜索在某些時候會比格子搜索好，二是了解貝葉斯優(yōu)化的機理。這里，談談我比賽和個人實踐中的體會，我很少會花過多時間在超參的調優(yōu)上，因為它帶來的收益是有限的，很多時候比起壓榨模型來說，思考和挖掘數(shù)據(jù)特征能帶來更多的收益，所以我想這也是為什么上面說：在任何想要調優(yōu)超參時，先用格子搜索或隨機搜索吧。總之，希望這篇文章對大家有幫助，我們下期再見~

參考資料

[1] sklearn.model_selection.GridSearchCV, 官方文檔: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.GridSearchCV.html#sklearn.model_selection.GridSearchCV

[2] Bergstra, J., & Bengio, Y. (2012). Random search for hyper-parameter optimization. Journal of machine learning research, 13(2).

[3] sklearn.model_selection.RandomizedSearchCV, 官方文檔: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.RandomizedSearchCV.html#sklearn.model_selection.RandomizedSearchCV

[4] Quora: How does Bayesian optimization work? - Duane Rich, 回答: https://www.quora.com/How-does-Bayesian-optimization-work

[5] Bayesian Optimization (2018). - Cse.wustl.edu. 課程Note: https://www.cse.wustl.edu/~garnett/cse515t/spring_2015/files/lecture_notes/12.pdf

[6] Hyperopt: Distributed Hyperparameter Optimization, 代碼: https://github.com/hyperopt/hyperopt#getting-started

[7] Bergstra, J., Bardenet, R., Bengio, Y., & Kégl, B. (2011, December). Algorithms for hyper-parameter optimization. In 25th annual conference on neural information processing systems (NIPS 2011) (Vol. 24). Neural Information Processing Systems Foundation.

[8] Li, L., Jamieson, K., DeSalvo, G., Rostamizadeh, A., & Talwalkar, A. (2017). Hyperband: A novel bandit-based approach to hyperparameter optimization. The Journal of Machine Learning Research, 18(1), 6765-6816.

[9] HpBandSter開源代碼庫, 代碼: https://github.com/automl/HpBandSte

[10] Hyperparameter Optimization for Machine Learning Models - Nagesh Singh Chauhan, 文章: [https://www.kdnuggets.com/2020/05/hyperparameter-optimization-machine-learning-models.html

[11] 為什么基于貝葉斯優(yōu)化的自動調參沒有大范圍使用？- 知乎, 問答: https://www.zhihu.com/question/33711002

干貨學習，點贊三連↓

機器學習調參自動優(yōu)化方法