機(jī)器學(xué)習(xí)基礎(chǔ)：用 Lasso 做特征選擇

Lasso 回歸是機(jī)器學(xué)習(xí)模型中的常青樹(shù)，在工業(yè)界應(yīng)用十分廣泛。在很多項(xiàng)目，尤其是特征選擇中都會(huì)見(jiàn)到他的影子。

Lasso 給簡(jiǎn)單線性回歸加了 L1 正則化，可以將不重要變量的系數(shù)收縮到 0 ，從而實(shí)現(xiàn)了特征選擇。本文重點(diǎn)也是在講解其原理后演示如何用其進(jìn)行特征選擇，希望大家能收獲一點(diǎn)新知識(shí)。

lasso 原理

Lasso就是在簡(jiǎn)單線性回歸的目標(biāo)函數(shù)后面加了一個(gè)1-范數(shù)

回憶一下：在線性回歸中如果參數(shù)θ過(guò)大、特征過(guò)多就會(huì)很容易造成過(guò)擬合，如下如所示：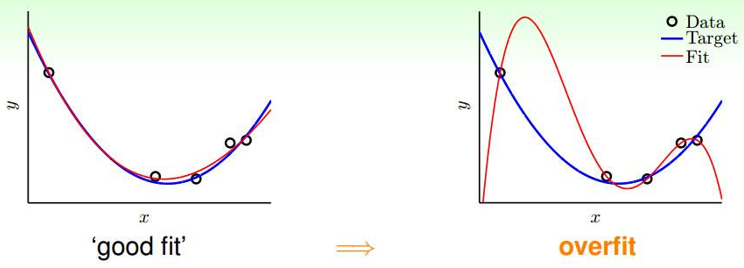

李宏毅老師的這張圖更有視覺(jué)沖擊力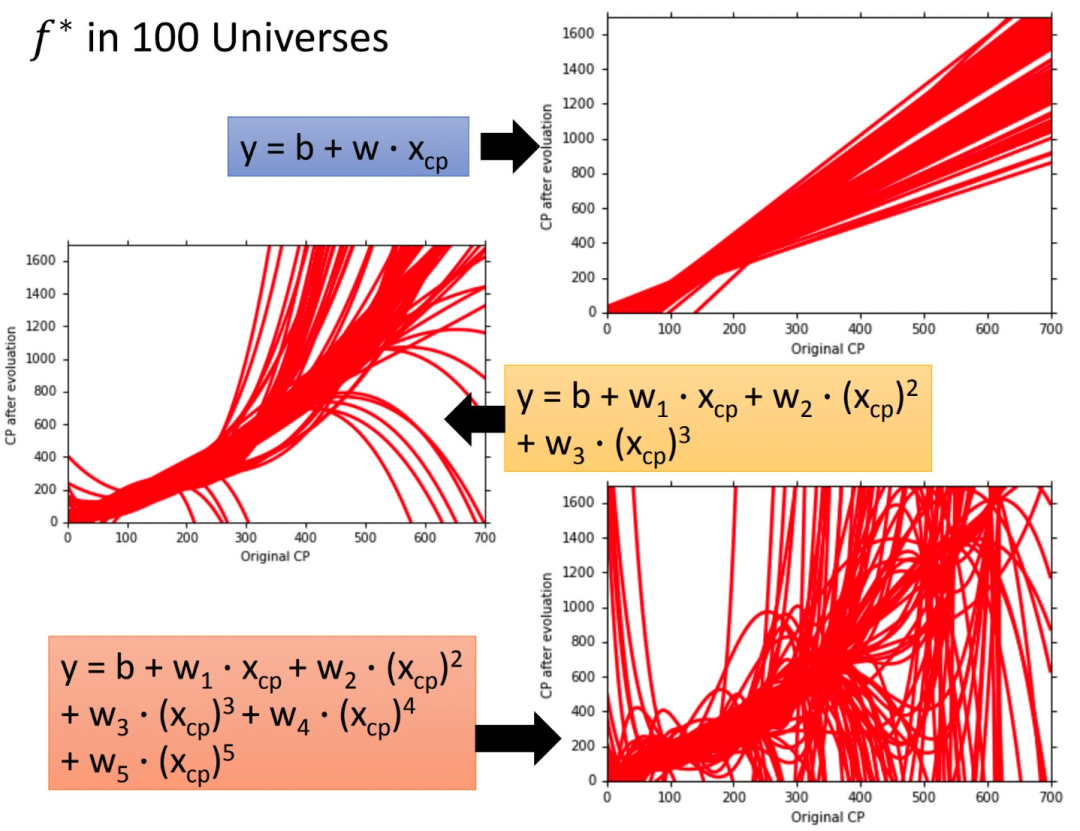

為了防止過(guò)擬合(θ過(guò)大)，在目標(biāo)函數(shù)后添加復(fù)雜度懲罰因子，即正則項(xiàng)來(lái)防止過(guò)擬合，增強(qiáng)模型泛化能力。正則項(xiàng)可以使用L1-norm(Lasso)、L2-norm(Ridge)，或結(jié)合L1-norm、L2-norm(Elastic Net)。

lasso回歸的代價(jià)函數(shù)

矩陣形式：

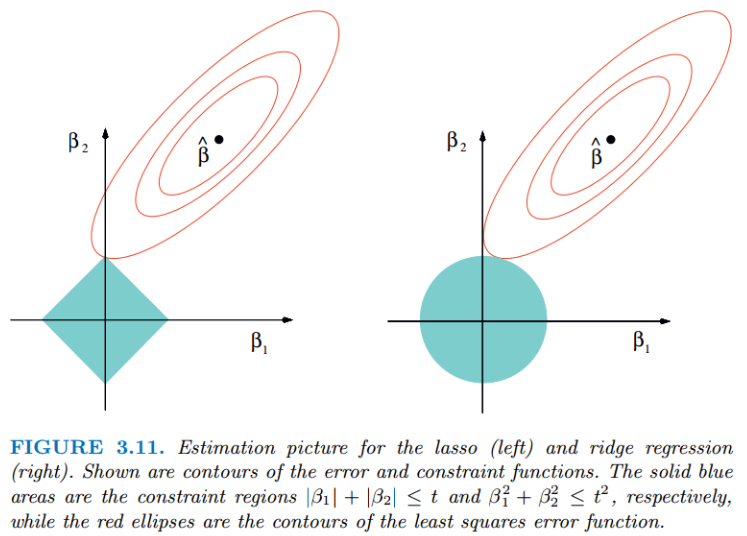
無(wú)論嶺回歸還是lasso回歸，本質(zhì)都是通過(guò)調(diào)節(jié)來(lái)實(shí)現(xiàn)模型誤差和方差的平衡調(diào)整。紅色的橢圓和藍(lán)色的區(qū)域的切點(diǎn)就是目標(biāo)函數(shù)的最優(yōu)解，可以看出Lasso的最優(yōu)解更容易切到坐標(biāo)軸上，形成稀疏結(jié)果（某些系數(shù)為零）。Ridge回歸在不拋棄任何一個(gè)特征的情況下，縮小了回歸系數(shù)，使得模型相對(duì)而言比較的穩(wěn)定，但和Lasso回歸比，這會(huì)使得模型的特征留的特別多，模型解釋性差。

今天我們的重點(diǎn)是Lasso，優(yōu)化目標(biāo)是：

上式不是連續(xù)可導(dǎo)的，因此常規(guī)的解法如梯度下降法、牛頓法、就沒(méi)法用了。常用的方法：坐標(biāo)軸下降法與最小角回歸法 (LARS)。

這部分就不展開(kāi)了，感興趣的同學(xué)可以看下劉建平老師的文章《Lasso回歸算法：坐標(biāo)軸下降法與最小角回歸法小結(jié) 》，這里不過(guò)多贅述。
https://www.cnblogs.com/pinard/p/6018889.html

想深入研究，可以看下Coordinate Descent和LARS的論文 https://www.stat.cmu.edu/~ryantibs/convexopt-S15/lectures/22-coord-desc.pdf
https://arxiv.org/pdf/math/0406456.pdf

scikit-learn 提供了這兩種優(yōu)化算法的Lasso實(shí)現(xiàn)，分別是

sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, 
normalize='deprecated', precompute=False, copy_X=True,
max_iter=1000, tol=0.0001, warm_start=False, 
positive=False, random_state=None, selection='cyclic')


sklearn.linear_model.lars_path(X, y, Xy=None, *, Gram=None,
max_iter=500, alpha_min=0, method='lar', copy_X=True, 
eps=2.220446049250313e-16, copy_Gram=True, verbose=0, 
return_path=True, return_n_iter=False, positive=False)

用 Lasso 找重要特征

在機(jī)器學(xué)習(xí)中，面對(duì)海量的數(shù)據(jù)，首先想到的就是降維，爭(zhēng)取用盡可能少的數(shù)據(jù)解決問(wèn)題，Lasso方法可以將特征的系數(shù)進(jìn)行壓縮并使某些回歸系數(shù)變?yōu)?，進(jìn)而達(dá)到特征選擇的目的，可以廣泛地應(yīng)用于模型改進(jìn)與選擇。

scikit-learn 的Lasso實(shí)現(xiàn)中，更常用的其實(shí)是LassoCV(沿著正則化路徑具有迭代擬合的套索（Lasso）線性模型)，它對(duì)超參數(shù)使用了交叉驗(yàn)證，來(lái)幫忙我們選擇一個(gè)合適的。不過(guò)GridSearchCV+Lasso也能實(shí)現(xiàn)調(diào)參，這里就列一下LassoCV的參數(shù)、屬性和方法。

### 參數(shù)
eps：路徑的長(zhǎng)度。eps=1e-3意味著alpha_min / alpha_max = 1e-3。
n_alphas:沿正則化路徑的Alpha個(gè)數(shù)，默認(rèn)100。
alphas：用于計(jì)算模型的alpha列表。如果為None，自動(dòng)設(shè)置Alpha。
fit_intercept：是否估計(jì)截距，默認(rèn)True。如果為False，則假定數(shù)據(jù)已經(jīng)中心化。
tol：優(yōu)化的容忍度，默認(rèn)1e-4：如果更新小于tol，優(yōu)化代碼將檢查對(duì)偶間隙的最優(yōu)性，并一直持續(xù)到它小于tol為止
cv：定交叉驗(yàn)證拆分策略

### 屬性

alpha_：交叉驗(yàn)證選擇的懲罰量
coef_：參數(shù)向量（目標(biāo)函數(shù)公式中的w）。
intercept_：目標(biāo)函數(shù)中的截距。
mse_path_：每次折疊不同alpha下測(cè)試集的均方誤差。
alphas_：對(duì)于每個(gè)l1_ratio，用于擬合的alpha網(wǎng)格。
dual_gap_：最佳a(bǔ)lpha（alpha_）優(yōu)化結(jié)束時(shí)的雙重間隔。
n_iter_ int：坐標(biāo)下降求解器運(yùn)行的迭代次數(shù)，以達(dá)到指定容忍度的最優(yōu)alpha。

### 方法

fit(X, y[, sample_weight, check_input]) 用坐標(biāo)下降法擬合模型。
get_params([deep]) 獲取此估計(jì)器的參數(shù)。
path(X, y, *[, l1_ratio, eps, n_alphas, …]) 計(jì)算具有坐標(biāo)下降的彈性網(wǎng)路徑。
predict(X) 使用線性模型進(jìn)行預(yù)測(cè)。
score(X, y[, sample_weight]) 返回預(yù)測(cè)的確定系數(shù)R ^ 2。
set_params(**params) 設(shè)置此估算器的參數(shù)。

Python實(shí)戰(zhàn)

波士頓房?jī)r(jià)數(shù)據(jù)為例

## 導(dǎo)入庫(kù) 
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso
import warnings
warnings.filterwarnings('ignore')
##  讀取數(shù)據(jù)
url = r'F:\100-Days-Of-ML-Code\datasets\Regularization_Boston.csv'
df = pd.read_csv(url)

scaler=StandardScaler()
df_sc= scaler.fit_transform(df)
df_sc = pd.DataFrame(df_sc, columns=df.columns)
y = df_sc['price']
X = df_sc.drop('price', axis=1) # becareful inplace= False
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)

Lasso調(diào)參數(shù)，主要就是選擇合適的alpha，上面提到LassoCV，GridSearchCV都可以實(shí)現(xiàn)，這里為了繪圖我們手動(dòng)實(shí)現(xiàn)。

alpha_lasso = 10**np.linspace(-3,1,100)
lasso = Lasso()
coefs_lasso = []

for i in alpha_lasso:
    lasso.set_params(alpha = i)
    lasso.fit(X_train, y_train)
    coefs_lasso.append(lasso.coef_)
    
plt.figure(figsize=(12,10))
ax = plt.gca()
ax.plot(alpha_lasso, coefs_lasso)
ax.set_xscale('log')
plt.axis('tight')
plt.xlabel('alpha')
plt.ylabel('weights: scaled coefficients')
plt.title('Lasso regression coefficients Vs. alpha')
plt.legend(df.drop('price',axis=1, inplace=False).columns)
plt.show()

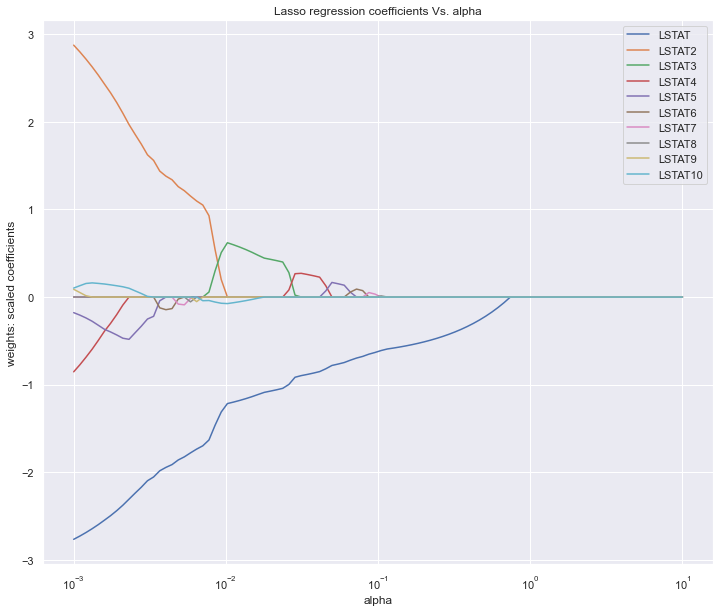圖中展示的是不同的變量隨著alpha懲罰后，其系數(shù)的變化，我們要保留的就是系數(shù)不為0的變量，alpha值不斷增大系數(shù)才變?yōu)?的變量在模型中越重要。

我們也可以按系數(shù)絕對(duì)值大小倒序看下特征重要性，可以設(shè)置更大的alpha值，就會(huì)看到更多的系數(shù)被壓縮為0了。

lasso = Lasso(alpha=10**(-3))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))

LSTAT2 2.876424
LSTAT 2.766566
LSTAT4 0.853773
LSTAT5 0.178117
LSTAT10 0.102558
LSTAT9 0.088525
LSTAT8 0.001112
dtype: float64

lasso = Lasso(alpha=10**(-2))
model_lasso = lasso.fit(X_train, y_train)
coef = pd.Series(model_lasso.coef_,index=X_train.columns)
print(coef[coef != 0].abs().sort_values(ascending = False))

LSTAT 1.220552
LSTAT3 0.625608
LSTAT10 0.077125
dtype: float64

或者直接畫個(gè)柱狀圖

fea = X_train.columns
a = pd.DataFrame()
a['feature'] = fea
a['importance'] = coef.values

a = a.sort_values('importance',ascending = False)
plt.figure(figsize=(12,8))
plt.barh(a['feature'],a['importance'])
plt.title('the importance features')
plt.show()

總結(jié)

Lasso回歸方法的優(yōu)點(diǎn)是可以彌補(bǔ)最小二乘估計(jì)法和逐步回歸局部最優(yōu)估計(jì)的不足，可以很好地進(jìn)行特征的選擇，有效地解決各特征之間存在多重共線性的問(wèn)題。

缺點(diǎn)是當(dāng)存在一組高度相關(guān)的特征時(shí)，Lasso回歸方法傾向于選擇其中的一個(gè)特征，而忽視其他所有的特征，這種情況會(huì)導(dǎo)致結(jié)果的不穩(wěn)定性。

雖然Lasso回歸方法存在弊端，但是在合適的場(chǎng)景中還是可以發(fā)揮不錯(cuò)的效果的。