CVPR 2022 Oral | 回歸標(biāo)簽不平衡? 試試Balanced MSE

在CVPR 2022上，商湯科技-南洋理工大學(xué)聯(lián)合AI研究中心S-Lab與新加坡國立大學(xué)的研究者針對不平衡回歸問題提出Balanced MSE損失函數(shù)。

標(biāo)簽不平衡經(jīng)常出現(xiàn)在現(xiàn)實世界中的視覺回歸問題中，而常用的MSE損失函數(shù)在預(yù)測少見標(biāo)簽時往往會產(chǎn)生很大的誤差。Balanced MSE從統(tǒng)計的視角解決標(biāo)簽的不平衡，同時適用于一維與多維回歸；其具有簡單、靈活的實現(xiàn)形式，不需要提前對標(biāo)簽分布進行計算也可以輕松接入訓(xùn)練中。

論文名稱：Balanced MSE for Imbalanced Visual Regression

論文地址：http://arxiv.org/pdf/2203.16427

項目地址：https://sites.google.com/view/balanced-mse/home

源碼地址：https://github.com/jiawei-ren/BalancedMSE

Balanced MSE的相關(guān)代碼目前已經(jīng)開源，歡迎各位同學(xué)使用和交流。

問題和挑戰(zhàn)

標(biāo)簽的不平衡是現(xiàn)實世界中視覺回歸里常見的問題，例如在年齡回歸問題中，可能大部分訓(xùn)練樣本都來自于成年人，老人與兒童的訓(xùn)練樣本則相對較少。

常用的Mean Square Error (MSE) 損失函數(shù)在少見樣本上的表現(xiàn)往往不盡如人意，因此越來越多的研究開始重視不平衡回歸，大規(guī)模評測集也在最近被提出[1]。相比于已經(jīng)被廣泛研究的不平衡分類，針對不平衡回歸的研究工作相對較少。較早的研究試圖通過生成的方法來增加少見標(biāo)簽的訓(xùn)練樣本[2]，但樣本生成在面對圖像等高維數(shù)據(jù)時可行性較低。

最近的研究主要采用重加權(quán)來提高少見標(biāo)簽在訓(xùn)練集中的權(quán)重[1]，但重加權(quán)在不平衡分類中已被證明效果有限[3]，我們也通過實驗在不平衡回歸上驗證了這一點。因此，不平衡回歸問題還處于一個起步階段，目前依然缺少行之有效的方法。

方法介紹

為了填補不平衡回歸方法的空白，我們提出了Balanced MSE損失函數(shù)，從統(tǒng)計的視角解決標(biāo)簽的不平衡。

1. 重新思考MSE損失函數(shù)

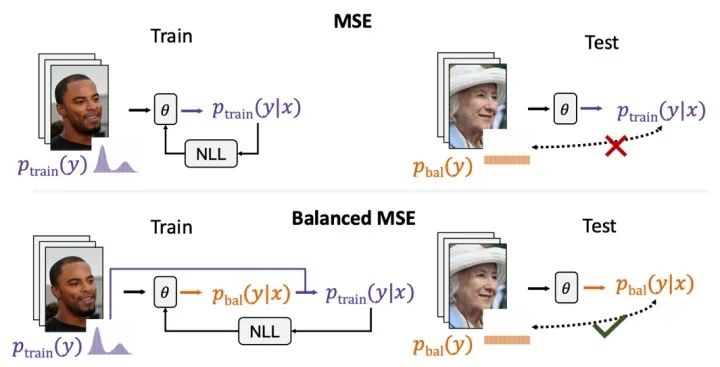
我們首先重新審視了常用的MSE損失函數(shù)，發(fā)現(xiàn)當(dāng)訓(xùn)練數(shù)據(jù)不平衡時，MSE會被標(biāo)簽分布所影響而傾向于預(yù)測常見的標(biāo)簽。當(dāng)測試集是平衡的或衡量指標(biāo)是平衡的時候，MSE的這一特點會導(dǎo)致模型在整體標(biāo)簽上的平均表現(xiàn)變差。我們沿著這個思路，使用概率的方法擺脫了不平衡的標(biāo)簽分布對MSE的影響。我們將改進后的損失函數(shù)稱作Balanced MSE。

2. 統(tǒng)一視角下的不平衡分類與回歸

其實從統(tǒng)計的視角解決標(biāo)簽不平衡的思路在不平衡分類中也被深入討論過，其中我們在NeurIPS 2020的工作Balanced Softmax [4]在長尾視覺分類上帶來了顯著的性能提升。然而由于MSE損失函數(shù)的概率意義很少被提及，這個思路在不平衡回歸問題上是首次被探討。

不僅如此，我們也通過我們的兩篇工作，Balanced Softmax與Balanced MSE，第一次將不平衡分類與不平衡回歸融入了統(tǒng)一的框架中討論。未來更多的不平衡分類技巧也可通過這個框架被引入不平衡回歸的領(lǐng)域中。

3. 靈活的實現(xiàn)

我們?yōu)锽alanced MSE中關(guān)于標(biāo)簽分布的積分計算提供了靈活的實現(xiàn)方式。我們提出的實現(xiàn)中既可以使用傳統(tǒng)的分段標(biāo)簽分布，也可以使用使用高斯混合模型擬合的標(biāo)簽分布，甚至可以不依賴任何預(yù)先處理的標(biāo)簽分布。

這里我們著重介紹不依賴預(yù)處理標(biāo)簽分布的實現(xiàn)方式，我們稱為BMC。BMC從每個訓(xùn)練batch中估計標(biāo)簽分布信息，因此不需要進行任何額外的操作即可替換常用的MSE損失函數(shù)。

BMC的形式也十分有趣，可以等價于將訓(xùn)練batch中對每個標(biāo)簽看作類別進行分類。其中，分類的logit由標(biāo)簽與預(yù)測之間的L2距離獲得，非常類似自監(jiān)督學(xué)習(xí)中使用的contrastive loss。得益于此，BMC可以簡單地通過分類中的的交叉熵?fù)p失函數(shù)快速實現(xiàn)。

實驗結(jié)果

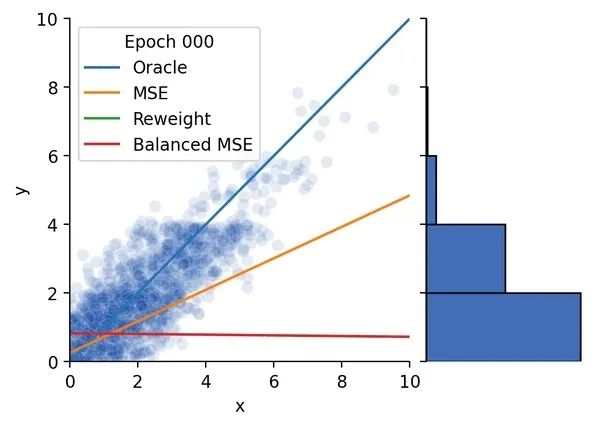
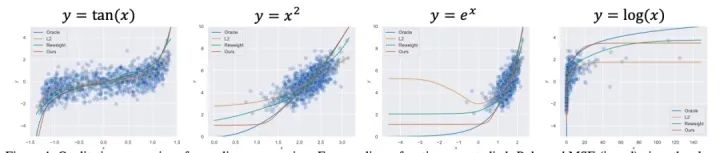
我們在首先使用合成數(shù)據(jù)集對Balanced MSE進行了實驗。圖4 展示了Balanced MSE在不同的標(biāo)簽分布下都能得到最接近真實線性關(guān)系的結(jié)果，而重加權(quán)方法的表現(xiàn)則隨著標(biāo)簽分布越來越不平衡變得越來越差。

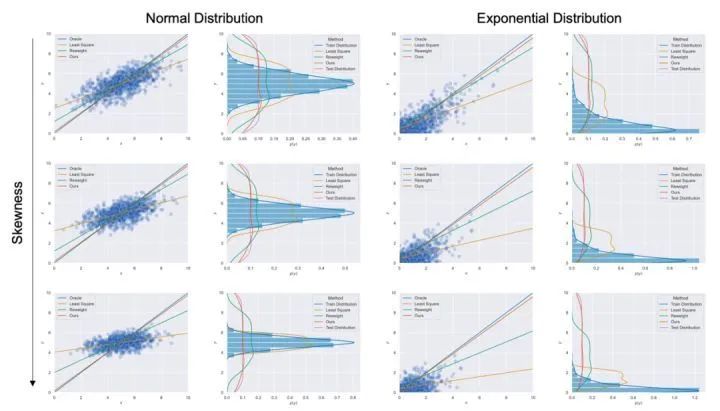
圖5和圖6分別展示了Balanced MSE在多維不平衡回歸與非線性不平衡回歸中依然能取得當(dāng)前最好的表現(xiàn)。

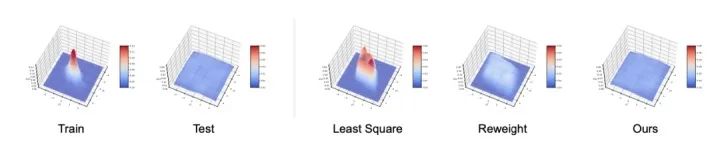
除此之外，我們在三個真實數(shù)據(jù)集上驗證了Balanced MSE的效果，其中包括包含兩個一維不平衡回歸問題：年齡回歸與深度回歸，以及一個我們提出的多維不平衡回歸問題：人體mesh估計[5]。

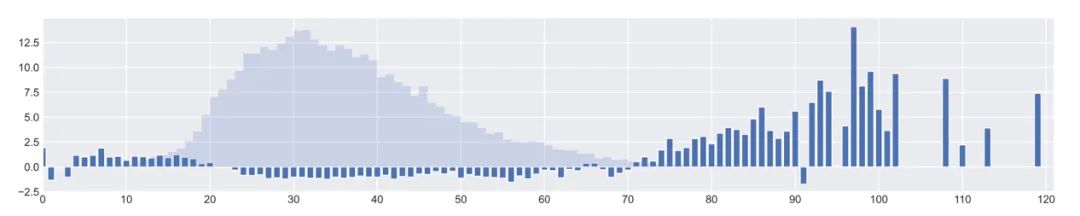
我們的方法均顯著超過了當(dāng)前的最優(yōu)算法。圖7中可以看到Balanced MSE顯著提升了對兒童和老人等少數(shù)群體的年齡估計表現(xiàn)。圖8顯示Balanced MSE可以有效估計少見的姿態(tài)，能夠幫助恢復(fù)出完整的動作幅度。

結(jié)語

我們針對不平衡回歸的問題設(shè)定，從統(tǒng)計的視角下重新思考了常用的MSE損失函數(shù)，發(fā)現(xiàn)MSE會受到不平衡標(biāo)簽分布的影響而做出不準(zhǔn)確的預(yù)測。為解決這個問題，我們提出了Balanced MSE損失函數(shù)，并給出了靈活的實現(xiàn)形式，包括不需要預(yù)先計算標(biāo)簽分布的實現(xiàn)。

Balanced MSE在一維與多維的不平衡回歸問題上都超過了最好的現(xiàn)有方法。結(jié)合我們之前的工作Balanced Softmax，我們?yōu)椴黄胶夥诸惻c回歸提供了一個統(tǒng)一的視角，希望更多的不平衡分類技巧可以借此引入不平衡回歸問題中。

作者信息

任嘉瑋 | 南洋理工大學(xué)S-Lab一年級博士生，導(dǎo)師是Ziwei Liu助理教授，以一作身份發(fā)表三篇頂會論文，曾獲得COCO 2019 全景分割挑戰(zhàn)冠軍。目前研究興趣是不平衡學(xué)習(xí)、3D表征學(xué)習(xí)和數(shù)字人。

公眾號后臺回復(fù)“CVPR 2022”獲取論文合集打包下載～

覺得有用麻煩給個在看啦~??