Vue 3.0 diff 算法及原理

轉(zhuǎn)自:GitHub - liuhanqu
Vue 3.0 采取的 diff 算法和 2.0 的雙端比較有點不同。大概的原理如下
// c1: a b [ c d e ] f g
// c2: a b [ d e c h ] f g
假如有如上的 c1 和 c2 新舊 children,在 diff 的時候,會有一個預(yù)處理的過程。
先從前往后比較,當(dāng)節(jié)點不同時,不再往后進(jìn)行比較。接著又從后往前進(jìn)行比較,當(dāng)節(jié)點不同時,不再往前進(jìn)行比較。
經(jīng)過預(yù)處理之后,c1 和 c2 真正需要進(jìn)行 diff 的部分如下所示:
// c1: c d e
// c2: d e c h
最后利用 “最長遞增子序列”,完成上述差異部分的比較,提高 diff 效率。
處理相同的前后節(jié)點
預(yù)處理過程代碼如下所示:
const patchKeyedChildren = (
c1,
c2,
container,
parentAnchor,
parentComponent,
parentSuspense,
isSVG,
optimized
) => {
let i = 0;
const l2 = c2.length
let e1 = c1.length - 1
let e2 = c2.length - 1
// 1. sync from start
while (i <= e1 && i <= e2) {
const n1 = c1[i]
const n2 = c2[i]
if (isSameVNodeType(n1, n2)) {
patch(
n1,
n2,
container,
parentAnchor,
parentComponent,
parentSuspense,
isSVG,
optimized
)
} else {
break
}
i++
}
// 2. sync from end
while (i <= e1 && i <= e2) {
const n1 = c1[e1]
const n2 = c2[e2]
if (isSameVNodeType(n1, n2)) {
patch(
n1,
n2,
container,
parentAnchor,
parentComponent,
parentSuspense,
isSVG,
optimized
)
} else {
break
}
e1--
e2--
}
}
僅有節(jié)點新增或移除
進(jìn)行預(yù)處理還有一個好處,就是在某些情況下,我們可以明確的知道有節(jié)點的新增或者刪除。
節(jié)點新增
i、e1、e2 滿足下述關(guān)系時,可以認(rèn)為是有節(jié)點新增
// 3. common sequence + mount
// (a b)
// (a b) c
// i = 2, e1 = 1, e2 = 2
// (a b)
// c (a b)
// i = 0, e1 = -1, e2 = 0
if (i > e1) {
if (i <= e2) {
const nextPos = e2 + 1;
const anchor = nextPos < l2 ? c2[nextPos] : parentAnchor
while (i <= e2) {
patch(
null,
c2[i],
container,
anchor,
parentComponent,
parentSuspense,
isSVG
)
i++
}
}
} else if {
//
} else {
//
}
節(jié)點移除
i、e1、e2 滿足下述關(guān)系時,可以認(rèn)為是有節(jié)點被移除
// 4. common sequence + unmount
// (a b) c
// (a b)
// i = 2, e1 = 2, e2 = 1
// a (b c)
// (b c)
// i = 0, e1 = 0, e2 = -1
if (i > e1) {
//
} else if (i > e2) {
while (i <= e1) {
unmount(c1[i], parentComponent, parentSuspense, true)
i++
}
} else {
//
}
有節(jié)點移動、新增或刪除
有時候情況可能沒有上述那么地簡單,即 i、e1、e2 并不滿足上述兩種情形時,我們就要尋找其中需要被移除、新增的節(jié)點,又或是判斷哪些節(jié)點需要進(jìn)行移動。
為此,我們需要去遍歷 c1 中還沒有進(jìn)行處理的節(jié)點,然后查看在 c2 中是否有對應(yīng)的節(jié)點(key 相同)。沒有,則說明該節(jié)點已經(jīng)被移除,那就執(zhí)行 unmount 操作。
首先,為了快速確認(rèn) c1 的節(jié)點在 c2 中是否有對應(yīng)的節(jié)點及所在的位置,對 c2 中的節(jié)點建立一個映射 (key: index)
// 5. unknown sequence
// [i ... e1 + 1]: a b [c d e] f g
// [i ... e2 + 1]: a b [d e c h] f g
// i = 2, e1 = 4, e2 = 5
if (i > e1) {
//
} else if (i > e2) {
//
} else {
const s1 = i
const s2 = i
const keyToNewIndexMap = new Map()
// 5.1 build key:index map for newChildren
for (i = s2; i <= e2; i++) {
const nextChild = c2[i]
if (nextChild.key !== null) {
keyToNewIndexMap.set(nextChild.key, i)
}
}
}
接著,定義以下幾個變量
let j
let patched = 0
const toBePatched = e2 - s2 + 1 // c2 中待處理的節(jié)點數(shù)目
let moved = false
// used to track whether any node has moved
let maxNewIndexSoFar = 0 // 已遍歷的待處理的 c1 節(jié)點在 c2 中對應(yīng)的索引最大值
// works as Map<newIndex, oldIndex>
// Note that oldIndex is offset by +1
// and oldIndex = 0 is a special value indicating the new node has
// no corresponding old node.
// used for determining longest stable subsequence
const newIndexToOldIndexMap = new Array(toBePatched) // 用于后面求最長遞增子序列
for (i = 0; i < toBePatched; i++) {
newIndexToOldIndexMap[i] = 0
}
然后,遍歷 c1 中待處理的節(jié)點,判斷否 c2 中是有相同 key 的節(jié)點存在。
沒有,說明該節(jié)點已經(jīng)被移除,unmount。 有,調(diào)用 patch 函數(shù)。并記錄節(jié)點在 c1 中的索引。同時,記錄節(jié)點在 c2 中的最大索引,假如節(jié)點在 c2 中的索引位置小于這個最大索引,那么說明是有元素需要進(jìn)行移動。
// 5.2 loop through old children left to be patched and try to patch
// matching nodes & remove nodes that are no longer present
for (i = s1; i <= e1; i++) {
const prevChild = c1[i]
// (A)
let newIndex
if (prevChild.key !== null) {
newIndex = keyToNewIndexMap.get(prevChild.key)
} else {
for (j = s2; i <= e2; j++) {
if (
newIndexToOldIndexMap[j - s2] === 0 &&
isSameVNodeType(prevChild, c2[j])
) {
newIndex = j
break
}
}
}
if (newIndex === void 0) {
unmount(prevChild, parentComponent, parentSuspense, true)
} else {
newIndexToOldIndexMap[newIndex - s2] = i + 1 // (B)
if (newIndex >= maxNewIndexSoFar) {
maxNewIndexSoFar = newIndex
} else {
moved = true
}
patch(
prevChild,
c2[i],
container,
null,
parentComponent,
parentSuspense,
isSVG,
optimized
)
patched++ // (C)
}
}
是不是 c1 中的所有節(jié)點都需要在 c2 中尋找對應(yīng)節(jié)點,然后調(diào)用 patch 呢。
注意到上面的代碼 (C),我們會更新已經(jīng) patched 的節(jié)點的數(shù)目,那么當(dāng) patched > toBePatched,可以認(rèn)為接下來遍歷的 c1 中的節(jié)點都是多余的了,直接移除就好。
所以在上面的 (A) 處需要補(bǔ)充一下代碼
if (patched >= toBePatched) {
// all new children have been patched so this can only be a removal
unmount(prevChild, parentComponent, parentSuspense, true)
continue
}
到這里,就是較難理解的部分了。
開篇我們說過,預(yù)處理過后,剩下的節(jié)點會借助最長遞增子序列來提高 diff 效率。
求解最長遞增子序列,主要的目的就是為了減少 dom 元素的移動,也可以理解為最少的 dom 操作。
首先,我們需要求解得到最長遞增子序列
// generate longest stable subsequence only when nodes have moved
const increasingNewIndexSequence = moved
? getSequence(newIndexToOldIndexMap)
: EMPTY_ARR
先看看這里的 newIndexToOldIndexMap 的值是什么。
結(jié)合一下具體的例子,假設(shè) c1 、c2 如下圖所示
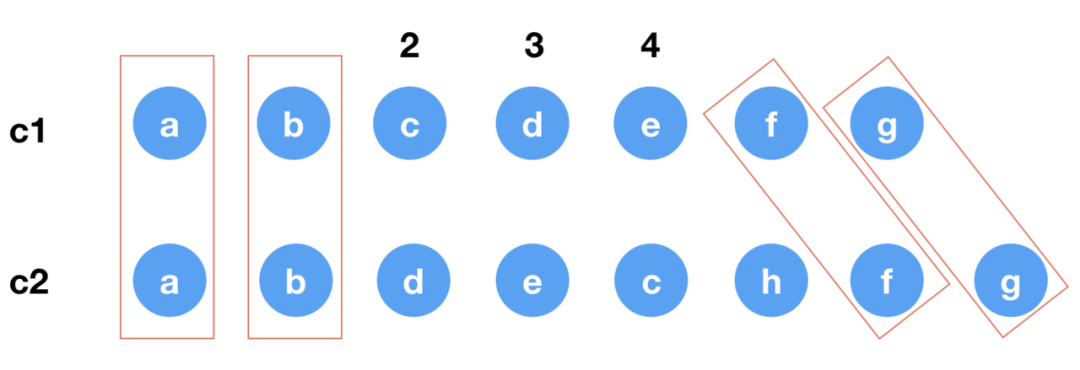
定義并初始化 newIndexToOldIndexMap
const newIndexToOldIndexMap = new Array(toBePatched)
for (i = 0; i < toBePatched; i++) {
newIndexToOldIndexMap[i] = 0
}
toBePatched 即預(yù)處理后,c2 中待處理的節(jié)點數(shù)目。對應(yīng)這里的例子,會有
toBePatched = 4
newIndexToOldIndexMap = [0, 0, 0, 0]
注意到上面 5.2 遍歷 c1 中節(jié)點的代碼的 (B) 處,有
// 這里是 i + 1,不是 i
// 因為 0 是一個特殊值,表示這個是新增的節(jié)點
newIndexToOldIndexMap[newIndex - s2] = i + 1 // (B)
所以處理完 c1 中的節(jié)點后,將有
moved = true
newIndexToOldIndexMap = [4, 5, 3, 0]
那么,increasingNewIndexSequence 的值就是 getSequence(newIndexToOldIndexMap)的返回值
// [4, 5, 3, 0] --> 最長遞增子序列是 [4, 5]
// 對應(yīng)的索引是 [0, 1]
increasingNewIndexSequence = [0, 1]
在求解得到最長遞增子序列之后,剩下的就是遍歷 c2 中的待處理節(jié)點,判斷是否節(jié)點是否屬于新增,是否需要進(jìn)行移動。
j = increasingNewIndexSequence.length - 1
// looping backwards so that we can use last patched node as anchor
// 注意:這里是從后往前遍歷
for (i = toBePatched - 1; i >= 0; i--) {
const nextIndex = s2 + i
const nextChild = c2[nextIndex]
const anchor =
nextIndex + 1 < l2 ? (c2[nextIndex + 1]).el : parentAnchor
// newIndexToOldIndexMap 里的值默認(rèn)初始化為 0
// 這里 === 0 表示 c2 中的節(jié)點在 c1 中沒有對應(yīng)的節(jié)點,屬于新增
if (newIndexToOldIndexMap[i] === 0) {
// mount new
patch(
null,
nextChild,
container,
anchor,
parentComponent,
parentSuspense,
isSVG
)
} else if (moved) {
// move if:
// There is no stable subsequence (e.g. a reverse)
// OR current node is not among the stable sequence
// j < 0 --> 最長遞增子序列為 []
if (j < 0 || i !== increasingNewIndexSequence[j]) {
move(nextChild, container, anchor, MoveType.REORDER)
} else {
j--
}
}
}
最長遞增子序列
在計算機(jī)科學(xué)中,最長遞增子序列(longest increasing subsequence)問題是指,在一個給定的數(shù)值序列中,找到一個子序列,使得這個子序列元素的數(shù)值依次遞增,并且這個子序列的長度盡可能地大。最長遞增子序列中的元素在原序列中不一定是連續(xù)的。-- 維基百科
對于以下的原始序列
0, 8, 4, 12, 2, 10, 6, 14, 1, 9, 5, 13, 3, 11, 7, 15
最長遞增子序列為
0, 2, 6, 9, 11, 15.
值得注意的是原始序列的最長遞增子序列并不一定唯一,對于該原始序列,實際上還有以下兩個最長遞增子序列
0, 4, 6, 9, 11, 15
0, 4, 6, 9, 13, 15
最后
至此,Vue 3.0 的 diff 代碼就分析完了,歡迎一起討論。
具體的代碼:https://github.com/vuejs/vue-next/blob/master/packages/runtime-core/src/renderer.ts
- EOF -
