阿里-測(cè)試開發(fā)面經(jīng)(四)
點(diǎn)擊藍(lán)字關(guān)注我們,獲取更多面經(jīng)

節(jié)點(diǎn)定義:
struct TreeNode{int val;TreeNode *left,*right;TreeNode(int val){this->val = val;this ->left = this->right = NULL;}};
先序遍歷
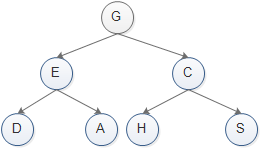
以上面這張圖為例樹的三種遍歷方式:
先序遍歷:先訪問根節(jié)點(diǎn),然后訪問左孩子,最后訪問右孩子。
所以,上面遍歷的結(jié)果是:GEDACHS。
1.遞歸實(shí)現(xiàn)
void preOrder(TreeNode *root){if (root==NULL)return;cout<<root->val<<endl;preOrder(root->left);preOrder(root->right);}
2.使用輔助棧
實(shí)現(xiàn)思路:1.將根節(jié)點(diǎn)入棧
2.每次從棧頂彈出一個(gè)節(jié)點(diǎn),訪問該節(jié)點(diǎn)
3.把當(dāng)前節(jié)點(diǎn)的右孩子入棧
4.把當(dāng)前節(jié)點(diǎn)的左孩子入棧
具體實(shí)現(xiàn):
void preOrder2(TreeNode *root){if (root == NULL)return;stack<TreeNode*> stk; //開辟一個(gè)棧空間stk.push(root);while(!stk.empty()){TreeNode* pNode = stk.pop();cout<<pNode->val;if (pNode->right!=NULL)stk.push(pNode->right);if (pNode->left!=NULL)stk.push(pNode->left);}}
3.Morris遍歷
Morris遍歷,常數(shù)的空間即可在O(n)時(shí)間內(nèi)完成二叉樹的遍歷。
O(1)空間進(jìn)行遍歷困難之處在于在遍歷的子結(jié)點(diǎn)的時(shí)候如何重新返回其父節(jié)點(diǎn)?
在Morris遍歷算法中,通過修改葉子結(jié)點(diǎn)的左右空指針來指向其前驅(qū)或者后繼結(jié)點(diǎn)來實(shí)現(xiàn)的。
其本質(zhì):線索二叉樹(Threaded Binary Tree),通過利用葉子節(jié)點(diǎn)空的right指針,指向中序遍歷的后繼節(jié)點(diǎn),從而避免了對(duì) stack 的依賴。
具體實(shí)現(xiàn):
void preOrder(TreeNode* root){if (root == NULL)return;TreeNode* pNode = root;while(pNode != NULL){if (pNode->left == NULL){cout<<pNode->val<<endl;pNode = pNode->right;}else{TreeNode* pPre = pNode->left;while(pPre->right != NULL && pPre->right != pNode){pPre = pPre->right;}if (pPre->right == NULL){/* code */pPre->right = pNode;cout<<pNode->val<<endl;pNode = pNode->left;}else{pPre->right = NULL;pNode = pNode->right;}}}}
中序遍歷
中序遍歷:先訪問左孩點(diǎn),然后訪問根節(jié)點(diǎn),最后訪問右孩子。
所以,上面遍歷的結(jié)果是:DEAGHCS。
1.遞歸實(shí)現(xiàn)
void InOrder(TreeNode *root){if (root==NULL)return;InOrder(root->left);cout<<root->val<<endl;InOrder(root->right);}
2.使用輔助棧
實(shí)現(xiàn)思路:
初始化一個(gè)二叉樹結(jié)點(diǎn)pNode指向根結(jié)點(diǎn);
若pNode非空,那么就把pNode入棧,并把pNode變?yōu)槠渥蠛⒆樱唬ㄖ钡阶钭筮叺慕Y(jié)點(diǎn))
若pNode為空,彈出棧頂?shù)慕Y(jié)點(diǎn),并訪問該結(jié)點(diǎn),將pNode指向其右孩子(訪問最左邊的結(jié)點(diǎn),并遍歷其右子樹)
具體實(shí)現(xiàn):
void InOrder(TreeNode *root){if (root==NULL){return;}stack<TreeNode*> stk;TreeNode *pNode = root;while(pNode!=NULL || !stk.empty()){if (pNode != NULL){stk.push(pNode);pNode = pNode->left;}else{pNode = stk.pop();stk.pop();cout<<pNode->val<<endl;pNode = pNode->right;}}}
3.Morris遍歷
實(shí)現(xiàn)思路:
1.如果當(dāng)前節(jié)點(diǎn)pNode的左孩子為空,那么輸出該節(jié)點(diǎn),并把該節(jié)點(diǎn)的右孩子作為當(dāng)前節(jié)點(diǎn)
2.如果當(dāng)前節(jié)點(diǎn)pNode的左孩子非空,那么找出該節(jié)點(diǎn)在中序遍歷的前驅(qū)結(jié)點(diǎn)prev
當(dāng)?shù)谝淮卧L問該前驅(qū)結(jié)點(diǎn)prev時(shí),其右孩子必定為空,那么就將其右孩子設(shè)置為當(dāng)前結(jié)點(diǎn),以便根據(jù)這個(gè)指針返回到當(dāng)前結(jié)點(diǎn)pNode中,并將當(dāng)前結(jié)點(diǎn)pNode設(shè)置為其左孩子;
當(dāng)該前驅(qū)結(jié)點(diǎn)pPre的右孩子為當(dāng)前結(jié)點(diǎn),那么就輸出當(dāng)前結(jié)點(diǎn),并把前驅(qū)結(jié)點(diǎn)的右孩子設(shè)置為空(恢復(fù)樹的結(jié)構(gòu)),將當(dāng)前結(jié)點(diǎn)更新為當(dāng)前結(jié)點(diǎn)的右孩子;
3.重復(fù)以上兩步,直到當(dāng)前結(jié)點(diǎn)為空。
具體實(shí)現(xiàn):
void InOrder(TreeNode *root){if (root == NULL)return;TreeNode* pNode = root;while(pNode != NULL){if (pNode->left == NULL){cout<<pNode->val<<endl;pNode = pNode->right;}else{TreeNode* pPre = pNode->left;while(pPre->right != NULL && pPre->right != pNode){pPre = pPre->right;}if (pPre->right == NULL){/* code */pPre->right = pNode;pNode = pNode->left;}else{pPre->right = NULL;cout<<pNode->val<<endl;pNode = pNode->right;}}}}
后序遍歷
后序遍歷:先訪問左孩子,然后訪問右孩子,最后訪問根節(jié)點(diǎn)。
所以,上面遍歷的結(jié)果是:DAEHSCG。
1.遞歸實(shí)現(xiàn)
void PostOrder(TreeNode *root){if (root==NULL)return;PostOrder(root->left);PostOrder(root->right);cout<<root->val<<endl;}
2.使用輔助棧
void postOrder(TreeNode *root) {if(root == NULL)return;stack<TreeNode *> stk;stk.push(root);TreeNode *prev = NULL;while(!stk.empty()) {TreeNode *pNode = stk.top();if(!prev || prev->left == pNode || prev->right == pNode) { // traverse downif(pNode->left)stk.push(pNode->left);else if(pNode->right)stk.push(pNode->right);/* else {cout << pNode->val << endl;stk.pop();}*/}else if(pNode->left == prev) { // traverse up from leftif(pNode->right)stk.push(pNode->right);}/* else if(pNode->right == prev) { // traverse up from rightcout << pNode->val << endl;stk.pop();}*/else {cout << pNode->val << endl;stk.pop();}prev = pNode;}}
雙輔助棧實(shí)現(xiàn)思路:
設(shè)置兩個(gè)棧stk, stk2;
將根結(jié)點(diǎn)壓入第一個(gè)棧stk;
彈出stk棧頂?shù)慕Y(jié)點(diǎn),并把該結(jié)點(diǎn)壓入第二個(gè)棧stk2;
將當(dāng)前結(jié)點(diǎn)的左孩子和右孩子先后分別入棧stk;
當(dāng)所有元素都?jí)喝雜tk2后,依次彈出stk2的棧頂結(jié)點(diǎn),并訪問之。
第一個(gè)棧的入棧順序是:根結(jié)點(diǎn),左孩子和右孩子;于是,壓入第二個(gè)棧的順序是:根結(jié)點(diǎn),右孩子和左孩子。
因此,彈出的順序就是:左孩子,右孩子和根結(jié)點(diǎn)。
void PostOrder2(TreeNode *root){ //兩個(gè)棧實(shí)現(xiàn)if (root == NULL)return;stack<TreeNode*> stk,stk2;stk.push(root);while(!stk.empty()){TreeNode* pNode = stk.top();stk.pop();stk2.push(pNode);// 將根節(jié)點(diǎn)壓棧if (pNode->left != NULL) // 如果左孩子不為空,則壓棧{stk.push(pNode->left);}if (pNode->right != NULL) // 如果左孩子不為空,則壓棧{stk.push(pNode->right);}}while(!stk2.empty()){cout<<stk2.top()->val<<endl;stk2.pop();}}
3.Morris遍歷實(shí)現(xiàn)
實(shí)現(xiàn)思路:
1.先建立一個(gè)臨時(shí)結(jié)點(diǎn)dummy,并令其左孩子為根結(jié)點(diǎn)root,將當(dāng)前結(jié)點(diǎn)設(shè)置為dummy;
2.如果當(dāng)前結(jié)點(diǎn)的左孩子為空,則將其右孩子作為當(dāng)前結(jié)點(diǎn);
3.如果當(dāng)前結(jié)點(diǎn)的左孩子不為空,則找到其在中序遍歷中的前驅(qū)結(jié)點(diǎn),
-如果前驅(qū)結(jié)點(diǎn)的右孩子為空,將它的右孩子設(shè)置為當(dāng)前結(jié)點(diǎn),將當(dāng)前結(jié)點(diǎn)更新為當(dāng)前結(jié)點(diǎn)的左孩子;
-如果前驅(qū)結(jié)點(diǎn)的右孩子為當(dāng)前結(jié)點(diǎn),倒序輸出從當(dāng)前結(jié)點(diǎn)的左孩子到該前驅(qū)結(jié)點(diǎn)這條路徑上所有的結(jié)點(diǎn)。將前驅(qū)結(jié)點(diǎn)的右孩子設(shè)置為空,將當(dāng)前結(jié)點(diǎn)更新為當(dāng)前結(jié)點(diǎn)的右孩子。
4.重復(fù)以上過程,直到當(dāng)前結(jié)點(diǎn)為空。
具體實(shí)現(xiàn):
void reverse(TreeNode* p1,TreeNode *p2){if (p1 == p2)return;TreeNode* x = p1;TreeNode* y = p1->right;while(true){TreeNode* tmp = y->right;y->right = x;x = y;y = tmp;if (x == p2)break;}}void printReverse(TreeNode* p1,TreeNode *p2){reverse(p1,p2);TreeNode* pNode = p2;while(true){cout<<pNode->val<<endl;if (pNode == p1)break;pNode = pNode->right;}reverse(p2,p1);}void PostOrder3(TreeNode* root){if(root == NULL)return;TreeNode *dummy = new TreeNode(-1);dummy->left = root;TreeNode *pNode = dummy;while(pNode != NULL) {if(pNode->left == NULL)pNode = pNode->right;else {TreeNode *pPrev = pNode->left;while(pPrev->right != NULL && pPrev->right != pNode)pPrev = pPrev->right;if(pPrev->right == NULL) {pPrev->right = pNode;pNode = pNode->left;}else {printReverse(pNode->left, pPrev);pPrev->right = NULL;pNode = pNode->right;}}}}
總結(jié)
上述三種遍歷方式時(shí)間復(fù)雜度和空間復(fù)雜度分析:
1.遞歸遍歷和非遞歸遍歷 時(shí)間復(fù)雜度0(n) 空間復(fù)雜度O(n)
2.Morris遍歷 時(shí)間復(fù)雜度0(n) 空間復(fù)雜度O(1)
更多面經(jīng)
掃描二維碼
獲取更多面經(jīng)
扶搖就業(yè)
