常見排序算法原理及JS代碼實(shí)現(xiàn)
來源:SegmentFault 思否社區(qū)
作者:Warren

本文只是將作者學(xué)習(xí)的過程以及算法理解進(jìn)行簡單的分享,提供多一個角度的理解說明,或許讓你的困惑能得以解決(代碼或說明若有問題,歡迎留言、聯(lián)系更正!以免造成更多困惑)
如果要更深入研究這些算法的同學(xué),社區(qū)中同類型更優(yōu)秀,單個算法更深入剖析的文章也是比比皆是,這里或許作為一個常見排序算法入門學(xué)習(xí)了解更準(zhǔn)確
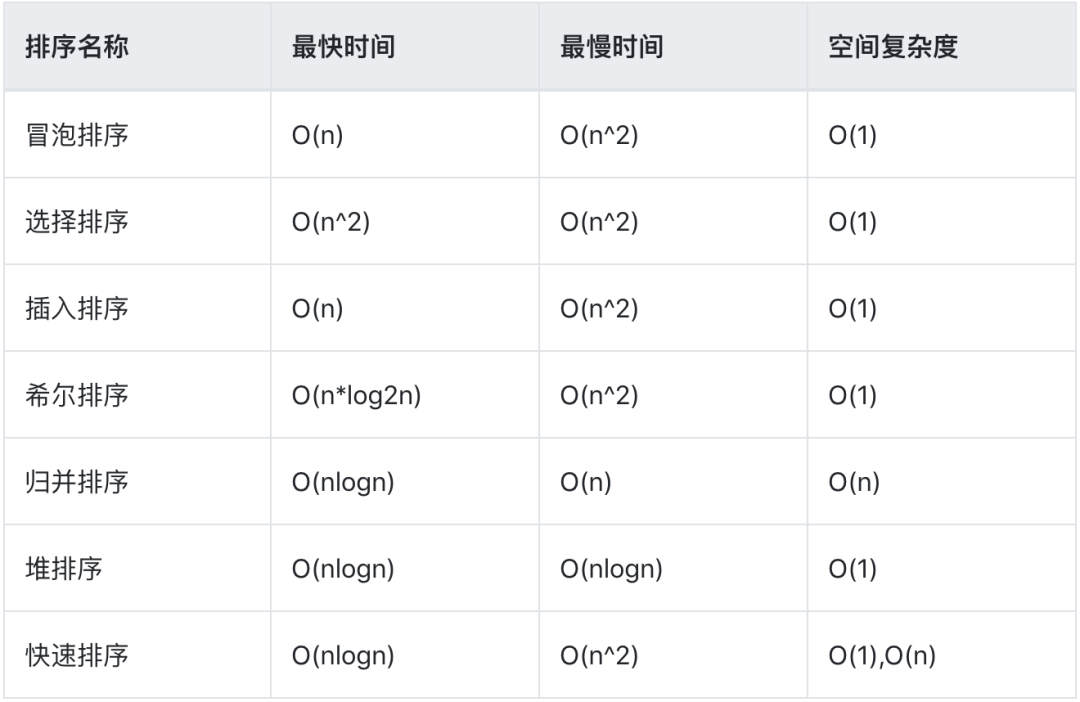
以上時間和空間復(fù)雜度會根據(jù)算法的優(yōu)化有所不同
生成測試所用,包含隨機(jī)十萬條數(shù)據(jù)的數(shù)組
const arr = []for (let i = 0; i < 100000; i++) {arr.push(Math.random())}
以下標(biāo)注的時間均為對該隨機(jī)數(shù)組的數(shù)據(jù)排序的時間,這里的時間只是作為一個參考,因?yàn)椴]有控制到只有唯一變量(每個排序算法用到的數(shù)組長度相同,但數(shù)組值不同),所以這里的時間只反應(yīng)常規(guī)情況
運(yùn)行時間的計算使用?console.time()
數(shù)組 sort() 方法
實(shí)現(xiàn)也是基于快排做了很多的優(yōu)化算法,以保障各種情況都能穩(wěn)定較快的實(shí)現(xiàn)排序?查看C++實(shí)現(xiàn)源碼
時間:≈ 75ms
function sortCompare(array) {array.sort((a, b) => (a-b))}
冒泡排序
原理:依次比較兩個相鄰的元素,將較大的放到右邊(升序排列)
一輪循環(huán)只找到一個最值,然后通過多次這樣的循環(huán)(所以有兩層嵌套循環(huán)),獲得一個排序結(jié)果
以下是經(jīng)過簡單優(yōu)化的算法實(shí)現(xiàn):
時間:≈ 21899ms
function bubbling(array) {const len = array.lengthlet sorted = true/* 每找到一個最值,需要一次循環(huán) */for (let i = 0; i < len; i++) {/* 必須每輪循環(huán)前,假設(shè)是排好序后的數(shù)組,防止只需要前幾次循環(huán)就排好的情況 */sorted = true/* 這里的循環(huán)是找出當(dāng)前輪的最值 *//* len-1-i 保障 j+1 能取到,同時放到最后的數(shù),不用參與下一輪的循環(huán),因?yàn)樗呀?jīng)是上一輪找出的最值 */for (let j = 0; j < len - 1 - i; j++) {if (array[j] > array[j + 1]) {let temp = array[j]array[j] = array[j + 1]array[j + 1] = tempsorted = false}}/* 如果是已經(jīng)排好序了就直接退出循環(huán),此時最優(yōu)時間復(fù)雜度 O(n) */if (sorted) break}return array}
選擇排序
原理:從剩余未排序序列中找到最小(大)元素,放置在已排序序列的末尾位置,以此循環(huán),直到所有元素均排序完畢
時間:≈ 6353ms
function selectionSort(array) {let len = array.lengthfor (let i = 0; i < len; i++) {/* 默認(rèn)開始的第一個值的位置放置下一個最小值 */let minIndex = i/* 查找剩余數(shù)值中的最小值,從 i + 1 開始的目的是避免與自身進(jìn)行一次比較 */for (let j = i + 1; j < len; j++) {if(array[minIndex] > array[j]) {minIndex = j}}/* 將最小值和當(dāng)前位置(i)的值進(jìn)行交換 */let temp = array[minIndex]array[minIndex] = array[i]array[i] = temp}return array}
插入排序
原理:將未排序隊(duì)列中的數(shù)值,逐個與已排序隊(duì)列中的數(shù)進(jìn)行比較,當(dāng)出現(xiàn)大于或小于已排序隊(duì)列中的某個數(shù)時,進(jìn)行插入操作
注意與選擇排序的區(qū)別,選擇排序是在未排序的數(shù)中找最值,然后交換位置,插入排序則是在已排序的的數(shù)中找對應(yīng)的第一個相對最值
時間:≈ 2416ms
function insertionSort(array) {let len = array.lengthfor (let i = 1; i < len; i++) {/* 記錄當(dāng)前未排序的數(shù),該數(shù)將會和有序數(shù)列中的數(shù)進(jìn)行比較 */let current = array[i]/* 有序數(shù)列的最后一個數(shù)(如果是從小到大排列,也就是最大的數(shù)) */let endIndex = i - 1while (endIndex >=0 && array[endIndex] > current) {/* 將有序數(shù)列中的數(shù),逐一與當(dāng)前未排序數(shù)進(jìn)行比較直到,找出比當(dāng)前未排序數(shù)小的數(shù)即停止 */array[endIndex + 1] = array[endIndex]endIndex--}/* 將最后一個往后移動空出來的位置賦值為,當(dāng)前未排序數(shù) */array[endIndex+1] = current}return array}
希爾排序
原理:
插入排序的一種優(yōu)化
設(shè)置一個增量,將數(shù)組中的數(shù)按此增量進(jìn)行分組(比如增量為4,那下標(biāo)為0,4,8...的數(shù)為一組) 對分組的數(shù)進(jìn)行插入排序 縮小增量 重復(fù)步驟1、2、3,直到增量為1 當(dāng)增量為1時,對整個數(shù)組進(jìn)行一次插入排序,輸出最后結(jié)果
時間復(fù)雜度與增量選取有關(guān),以下算法時間復(fù)雜度為 O(n^(3/2))
非穩(wěn)定排序(2個相等的數(shù),在排序完成后,原來在前面的數(shù)還是在前面,即為穩(wěn)定排序)
時間:≈ 35ms
function shellSort(array) {let len = array.length, gap = 1;/* 此處獲取一個最大增量,增量的獲取方法不固定,這里采用比較常見的方式,一定要保證最后能取到1 */while(gap < len/3) {gap = gap*3+1;}/* 每更新一次增量就進(jìn)行一次插入排序 */while(gap>0) {/* 以下邏輯與插入排序一致,當(dāng)增量變?yōu)?時即完全一致 */for (let i = gap; i < len; i++) {/* 這里要循環(huán)到數(shù)組最后是因?yàn)橐U袭?dāng)前分組中的每一個數(shù)都經(jīng)過排序,所以當(dāng)前分組靠前的數(shù)據(jù)會被與后面的數(shù)據(jù)進(jìn)行多次排序 */let current = array[i]let endIndex = i - gapwhile(endIndex>=0 && array[endIndex] > current) {array[endIndex + gap] = array[endIndex]endIndex -= gap}array[endIndex+gap] = current}gap = Math.floor(gap/3)}return array}
分治法:把一個復(fù)雜的問題分成兩個或更多的相同或相似的子問題,再把子問題分成更小的子問題……直到最后子問題可以簡單的直接求解,原問題的解即子問題的解的合并
歸并排序
原理:將當(dāng)前數(shù)組,遞歸分組,比較大小后再一 一合并分組,是采用分治法的一個應(yīng)用
獲取一個中間位置的值,然后以該位置為中心點(diǎn)分組 遞歸進(jìn)行分組 比較當(dāng)前兩個分組,將其合并為一個數(shù)組
時間:≈ 1170ms
function mergeSort(array) {const len = array.lengthif(len<2) return arrayconst middle = Math.floor(len/2)/* 取中間值進(jìn)行分組 */const left = array.slice(0, middle)const right = array.slice(middle)/* 遞歸分組 */return merge(mergeSort(left), mergeSort(right))}function merge(left, right) {const result = []/* 兩個分組都有值時,逐個進(jìn)行比較 */while (left.length && right.length) {if(left[0] <= right[0]) {result.push(left.shift())} else {result.push(right.shift())}}/* 只有一個分組時,表明其全部為最大值,直接全部放入結(jié)果數(shù)組即可 */if(left.length){result.push(...left)}if(right.length){result.push(...right)}return result}
堆排序
分為大頂堆(子節(jié)點(diǎn)都小于父節(jié)點(diǎn)),小頂堆(子節(jié)點(diǎn)都大于父節(jié)點(diǎn))
原理:
根據(jù)給定的數(shù)據(jù)創(chuàng)建堆 將堆頂和堆尾互換,將堆長度減1 遞歸步驟1、2
時間:≈ 46ms
function heapSort(array) {let length = array.length/* 第一個非葉子節(jié)點(diǎn)(葉子節(jié)點(diǎn):沒有子節(jié)點(diǎn)的節(jié)點(diǎn)):n/2 -1 *//* 為什么從這個點(diǎn)開始,也是因?yàn)檫@是最后一個擁有子節(jié)點(diǎn)的父節(jié)點(diǎn),其可能會發(fā)生父子節(jié)點(diǎn)交換 */const node = Math.floor(length/2) - 1/* 第一步先將數(shù)組構(gòu)建為堆 這里是大頂堆 */for (let i = node; i >= 0 ; i--) {maxHeap(array, i, length)}/* 第二步 將堆頂元素與堆尾元素交換 再將前 (n-1) 個數(shù)重復(fù)構(gòu)建堆 */for (let j = length - 1; j > 0; j--) {swap(array, 0, j)length--/* 這里相當(dāng)于把第一個葉子節(jié)點(diǎn)改變了,所以下面從 0 開始, 當(dāng)前堆的堆尾前一個數(shù)為結(jié)束 重新構(gòu)建堆 */maxHeap(array, 0, length)}return array}function maxHeap(array, i, length) {/* 左子節(jié)點(diǎn) */let left = i*2 + 1/* 右子節(jié)點(diǎn) */let right = i*2 + 2/* 父節(jié)點(diǎn) */let parent = i/* 找出子節(jié)點(diǎn)中比父節(jié)點(diǎn)大的數(shù)進(jìn)行交換 */if(left < length && array[left] > array[parent]) {parent = left}/* 這里兩個條件都觸發(fā)也沒有關(guān)系,只要保障,一個比父節(jié)點(diǎn)大的子節(jié)點(diǎn)被移上去即可 */if(right < length && array[right] > array[parent]) {parent = right}if(parent !== i) {swap(array,i, parent)/* 表示有數(shù)據(jù)移動,所以要重排一下數(shù)據(jù)移動后,所影響到的父子節(jié)點(diǎn),也就是此時的 parent 節(jié)點(diǎn)和其子節(jié)點(diǎn) */maxHeap(array, parent, length)}}function swap(arr, i, j) {var temp = arr[i];arr[i] = arr[j];arr[j] = temp;}
快速排序
原理:
在數(shù)組中找一個基準(zhǔn) 數(shù)組中的數(shù)與該基準(zhǔn)相比較,比它小的放在其前面,比它大的放在其后面(分區(qū)操作) 再遞歸的去操作基準(zhǔn)前、后的分區(qū)
方式一:
需要 O(n) 的額外存儲空間,和歸并排序一樣
但是代碼更清晰的體現(xiàn)快排的思想
時間:≈ 77ms
function quickSort (array) {if (array.length < 2) return array;const pivot = array[0];let left = []let right = []for (let i = 1, length = array.length; i < length; i++) {if(array[i] < pivot) {left.push(array[i])} else {right.push(array[i])}}return quickSort(left).concat([pivot], quickSort(right));}
方式二:
原地排序
時間:≈ 34ms
function quickSort(array, left, right) {if(left<right) {pivotIndex = fill(array, left, right)quickSort(array, left, pivotIndex-1)quickSort(array, pivotIndex+1, right)}return array}function fill(array, left, right) {const pivotValue = array[left]while(left < right){/* 右邊大于基準(zhǔn)的數(shù)據(jù)不需要移動位置 *//* 這里或下面的循環(huán),一定要確保有一處把相等的情況包含在內(nèi) */while(array[right] >= pivotValue && left < right){right--}/* 將右邊第一個掃描到的小于基準(zhǔn)的數(shù)據(jù)移動到左邊的空位 */array[left] = array[right]/* 左邊小于基準(zhǔn)的數(shù)據(jù)不需要移動位置 */while(array[left] < pivotValue && left < right){left++}array[right] = array[left]}/* 這里right和left 相等了 */array[right] = pivotValuereturn right}
還有一些更好的優(yōu)化,比如基準(zhǔn)數(shù)的選取,避免最壞時間復(fù)雜度情況的發(fā)生,可自行探索
總結(jié):
在實(shí)際項(xiàng)目中可能直接用到這些算法就能解決掉業(yè)務(wù)需求的情況并不多,甚至直接用 Array.sort()?也能解決。
但是業(yè)務(wù)需求千變?nèi)f化,多種多樣,總有需要你從底層去更改、優(yōu)化、變異算法的情況,此時就需要用你理解的這些基本算法的原理來快速解決業(yè)務(wù)問題。

