點(diǎn)擊上方“程序員大白”，選擇“星標(biāo)”公眾號(hào)
重磅干貨，第一時(shí)間送達(dá)

跳表(SkipList)

簡(jiǎn)介

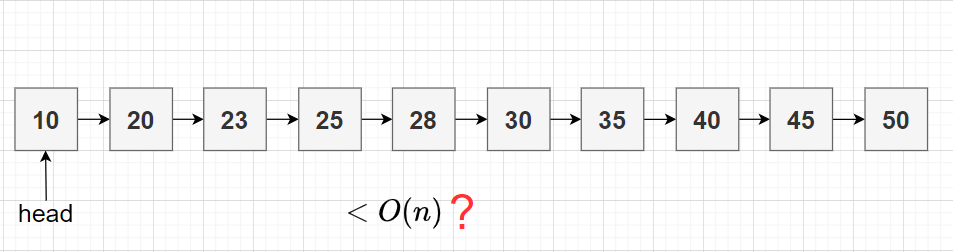
首先，我們?cè)谛睦锼伎家粋€(gè)問(wèn)題：排序單鏈表的查找時(shí)間復(fù)雜度能否比好呢？

對(duì)于一個(gè)已經(jīng)排好序的單鏈表來(lái)說(shuō)，想要查詢其中的一個(gè)數(shù)據(jù)，也只能從頭開(kāi)始遍歷鏈表，不能跳過(guò)節(jié)點(diǎn)（skip nodes）查找，這樣效率很低，時(shí)間復(fù)雜度為。

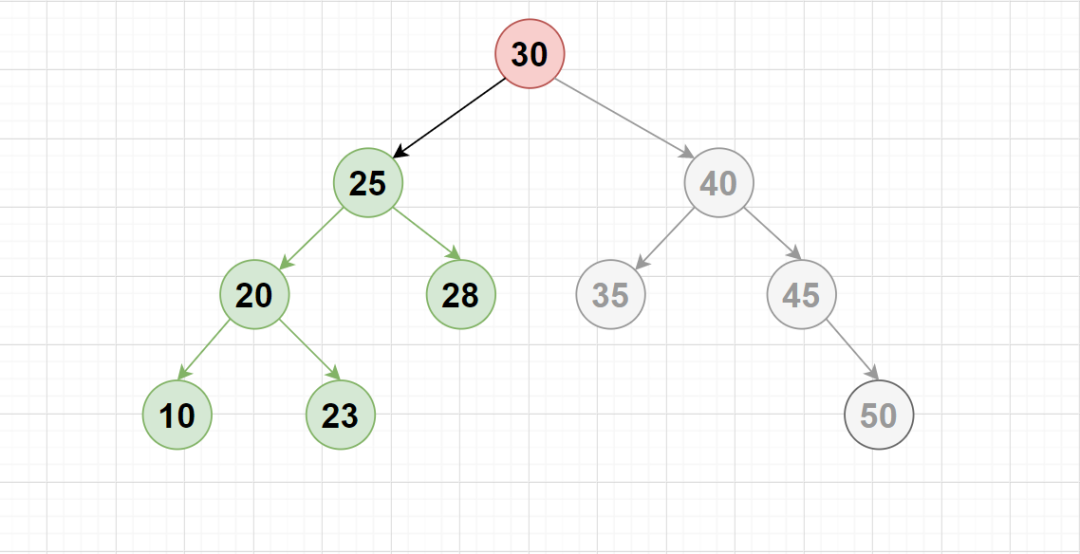
如上圖所示，對(duì)于平衡二叉搜索樹(shù)（AVL 樹(shù)），在與根進(jìn)行一次比較后，我們跳過(guò)了幾乎一半的節(jié)點(diǎn)。

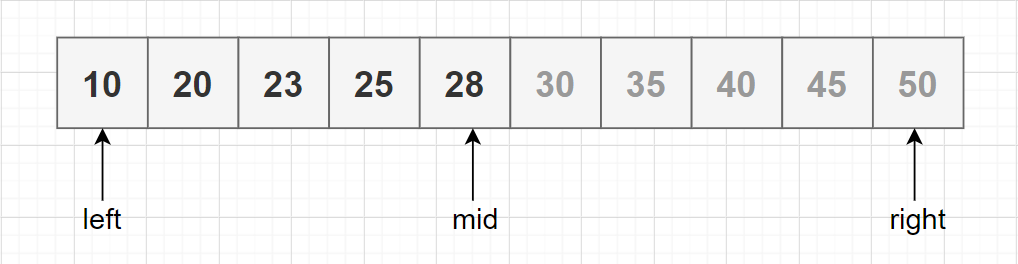
對(duì)于排序的數(shù)組，我們可以隨機(jī)訪問(wèn)，并且可以對(duì)數(shù)組應(yīng)用二分查找法。

那我們是不是可以對(duì)排序單鏈表進(jìn)行增強(qiáng)（比如像二分查找一樣）來(lái)提高查找速度呢？那就是 跳表（Skip List）。

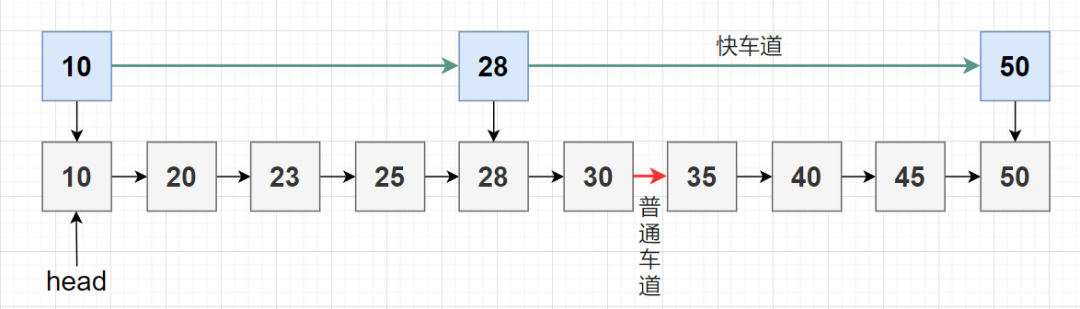
這個(gè)想法很簡(jiǎn)單，我們通過(guò)創(chuàng)建多層鏈表，這樣我們就可以跳過(guò)一些節(jié)點(diǎn)。

如上圖中例子，其中包含 10個(gè)節(jié)點(diǎn)和兩層。上層是只連接主要車(chē)站的 “快車(chē)道”，下層是連接每個(gè)車(chē)站的 “普通車(chē)道”。就像你從北京出發(fā)，自駕到西藏，如果你走 “國(guó)道”，你可能要路過(guò)很多站點(diǎn)，速度也會(huì)比較慢；但是也有直達(dá)的 “高速公路” 呀（京藏高速），高速公路上的出站口少，但是你到達(dá)目的地更快呀。

假設(shè)我們要查找 35，我們從“快車(chē)道” 的第一個(gè)節(jié)點(diǎn)開(kāi)始，一直沿著“快車(chē)道”前進(jìn)，直到找到下一個(gè)節(jié)點(diǎn)大于 35 的節(jié)點(diǎn)。一旦我們?cè)凇翱焖佘?chē)道”上找到這樣的節(jié)點(diǎn)( 28 就是我們找到的節(jié)點(diǎn)，28 的下一個(gè)節(jié)點(diǎn) 50 大于 35)，我們就使用節(jié)點(diǎn) 28 的指針移動(dòng)到 “普通車(chē)道” ，并在 “普通車(chē)道” 上線性查找 35 。在圖中的例子中，我們從“普通車(chē)道”上的 28 開(kāi)始，通過(guò)線性搜索，我們找到了 35。

原本需要 6 次才能查找到元素 35 ，現(xiàn)在僅查找了 4 次。

那么圖中的兩層情況下的時(shí)間復(fù)雜度是多少？

最壞情況下的時(shí)間復(fù)雜度是“快車(chē)道”上的節(jié)點(diǎn)數(shù)加上“普通車(chē)道”上的一個(gè)段（段表示兩個(gè)“快車(chē)道”節(jié)點(diǎn)之間的“普通車(chē)道”節(jié)點(diǎn)的數(shù)目）的節(jié)點(diǎn)數(shù)。

因此，如果我們?cè)凇罢＼?chē)道”上有 n 個(gè)節(jié)點(diǎn)，在“快速車(chē)道”上有節(jié)點(diǎn)，并且我們將 “普通車(chē)道” 均分，那么在 “普通車(chē)道” 的每一段中都有個(gè)節(jié)點(diǎn)。實(shí)際上是具有兩層跳表結(jié)構(gòu)的最優(yōu)除法。通過(guò)這種規(guī)則，搜索遍歷鏈表節(jié)點(diǎn)將為。因此，在增加空間的情況下，可以將時(shí)間復(fù)雜度降低到。

那么我們能將時(shí)間復(fù)雜度降得更低嗎？

通過(guò)增加更多的層可以進(jìn)一步降低跳表的時(shí)間復(fù)雜度。實(shí)際上，在個(gè)額外空間的情況下，查找、插入和刪除的期望時(shí)間復(fù)雜度都可以達(dá)到。

跳表的插入操作

在深入理解跳表的插入操作之前，一定要解決跳表的層數(shù)問(wèn)題！！！

層數(shù)的確定

鏈表中的每個(gè)元素都由一個(gè)節(jié)點(diǎn)表示，節(jié)點(diǎn)的層級(jí)是在插入鏈表時(shí)隨機(jī)選擇的。跳表中節(jié)點(diǎn)的層級(jí)不取決于節(jié)點(diǎn)中的元素?cái)?shù)量，而是由下面一個(gè)算法確定的，算法的 Java 代碼為：

private int randomLevel() {
 int level = 1; 
    while (Math.random() < P && level < MaxLevel {
        level++;
    }
    return level;
}

MaxLevel 是跳表層數(shù)的上限。它可以確定為，是中的節(jié)點(diǎn)總數(shù)。上述算法保證了隨機(jī)層數(shù)永遠(yuǎn)不會(huì)大于 MaxLevel 。這里 P 是第 i+1 層節(jié)點(diǎn)的個(gè)數(shù)與第 i 層節(jié)點(diǎn)個(gè)數(shù)的比值，比如，就表示第 i 層的節(jié)點(diǎn)個(gè)數(shù)是第 i+1 層節(jié)點(diǎn)個(gè)數(shù)的兩倍，理論情況下如下圖所示，跳表可以和 AVL 樹(shù)達(dá)到幾乎一樣的效果：

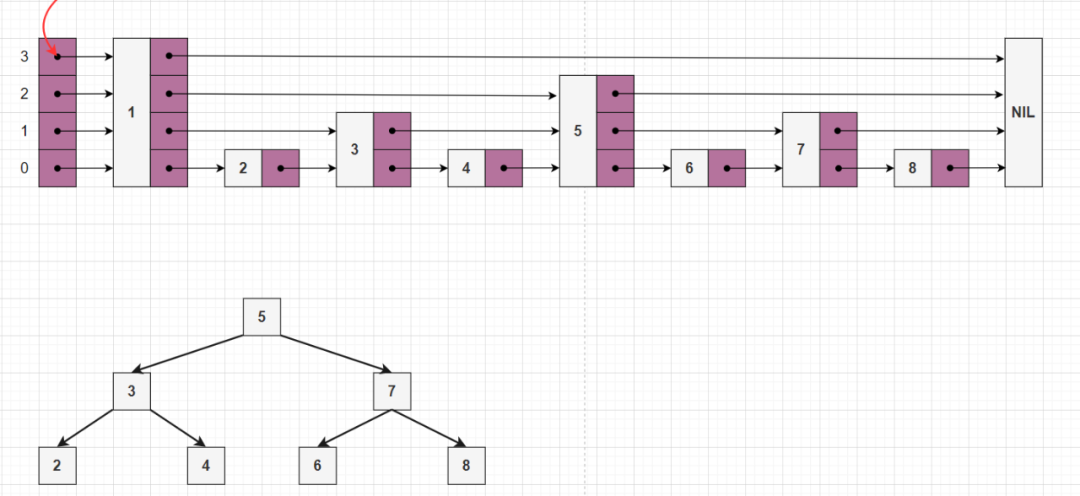
理論來(lái)講，對(duì)于，一級(jí)索引中元素個(gè)數(shù)應(yīng)該占原始數(shù)據(jù)的 50% （原始數(shù)據(jù) 8 個(gè)，第一層索引 4 個(gè)），二級(jí)索引中元素個(gè)數(shù)占原始的 25%，三級(jí)索引占原始數(shù)據(jù)的 12.5% ，一直到最頂層。

對(duì)于每一個(gè)新插入的節(jié)點(diǎn)，都需要調(diào)用 randomLevel() 生成一個(gè)合理的層數(shù)。該randomLevel() 方法會(huì)隨機(jī)生成 1 ~ MaxLevel 之間的數(shù)，且：的概率返回 1，的概率返回 2，的概率返回 3 ...

節(jié)點(diǎn)結(jié)構(gòu)

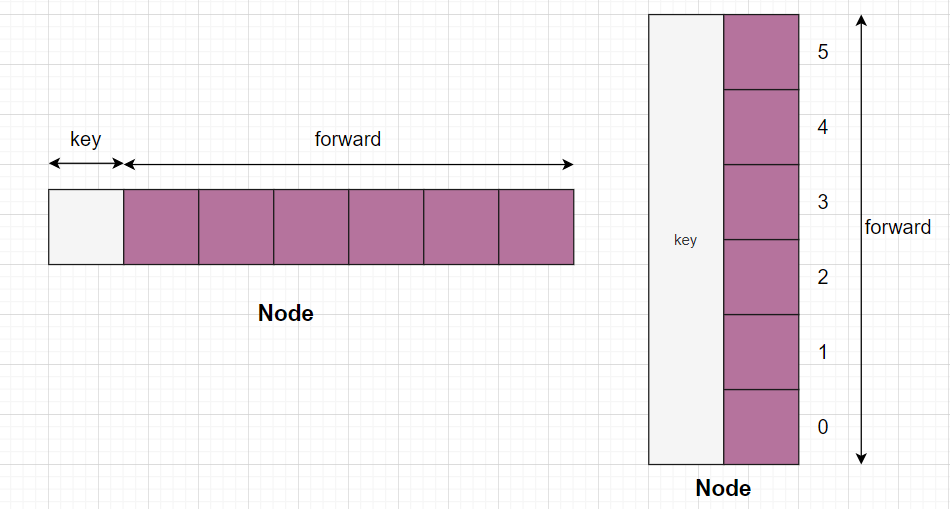
每個(gè)節(jié)點(diǎn)由一個(gè)關(guān)鍵字 key 和一個(gè)前向數(shù)組 forwards[] 組成，該數(shù)組存儲(chǔ)指向不同層的節(jié)點(diǎn)的指針。i 層的節(jié)點(diǎn)的前向數(shù)組保存了從第 0 層到第 i 層前向節(jié)點(diǎn)的指針。

public class Node {
        private int key = -1; //結(jié)點(diǎn)的 key 
        private Node forwards[] = new Node[MAX_LEVEL];  // 結(jié)點(diǎn)key 所對(duì)應(yīng)的前向數(shù)組
}

插入操作

我們將從列表的最高層開(kāi)始，將當(dāng)前節(jié)點(diǎn)的下一個(gè)節(jié)點(diǎn)的 key 與要插入的 key 進(jìn)行比較。基本思想是：

如果下一個(gè)節(jié)點(diǎn)的 key 小于要插入的 key ，則我們?cè)谕粚由侠^續(xù)前進(jìn)查找。
如果下一個(gè)節(jié)點(diǎn)的 key 大于要插入的 key ，則我們將指向當(dāng)前節(jié)點(diǎn) i 的指針存儲(chǔ)在 update[i] 處，并向下移動(dòng)一層，繼續(xù)搜索。

在第 0 層，我們一定會(huì)找到一個(gè)位置來(lái)插入給定的 key 。

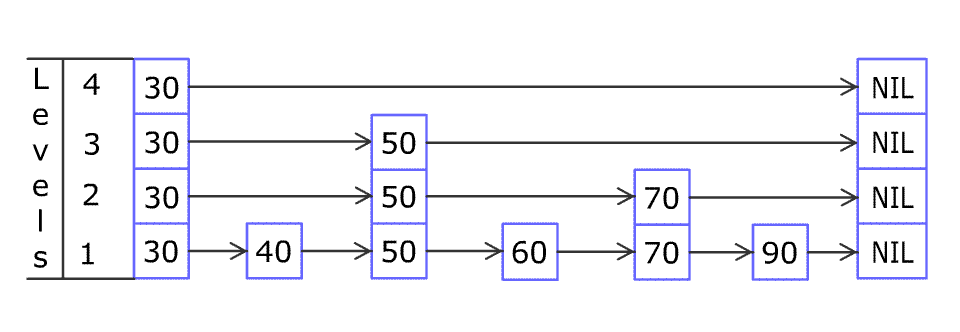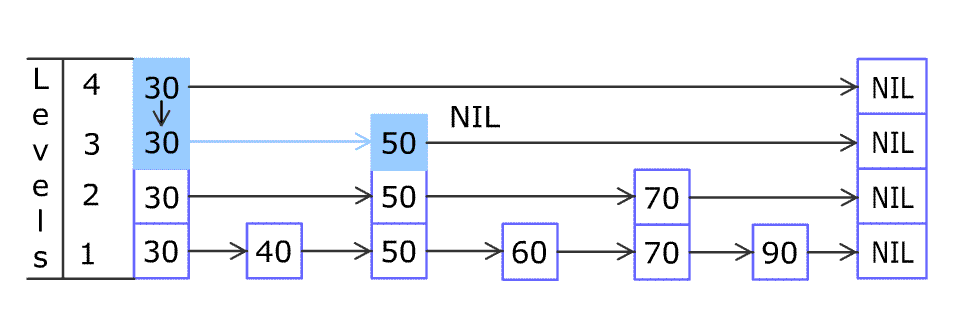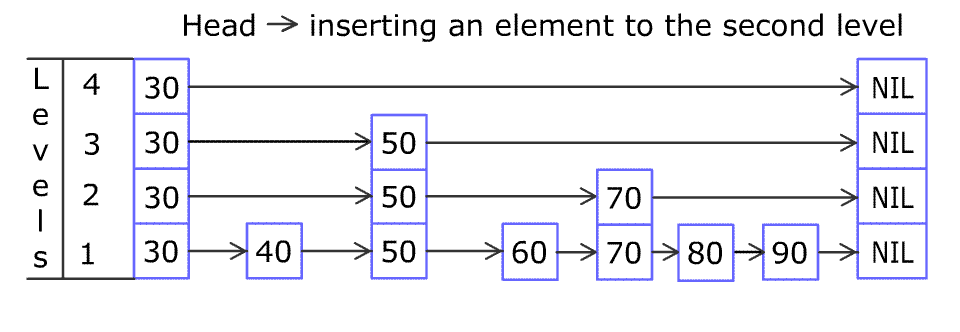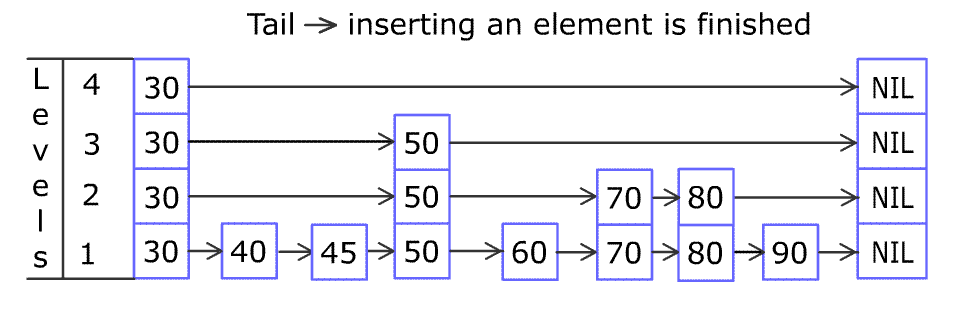
以下是插入操作的偽代碼：

public void insert(int key) {
    int level = randomLevel();
    Node newNode = new Node();
    newNode.key = key;
    newNode.maxLevel = level;
    // 創(chuàng)建 update 數(shù)組并初始化
    Node update[] = new Node[level];
    for (int i = 0; i < level; ++i) {
        update[i] = head;
    }
    // 將查找路徑上結(jié)點(diǎn)的前向結(jié)點(diǎn)設(shè)置為新插入結(jié)點(diǎn)
    Node current = head;
    for (int i = level - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < key) {
            current = current.forwards[i];
        }
        update[i] = current;// 第 i 層需要修改的節(jié)點(diǎn)為 p
    }
    current = current.forwards[0];
    if (current == null || current.key != key) {
        // 在第0到level層插入新結(jié)點(diǎn)
        for (int i = 0; i < level; ++i) {
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }
    }
    // 更新跳表的層數(shù)
    if (currentLevel < level) currentLevel = level;
}

在這里，update[i] 表示插入值為 key 的節(jié)點(diǎn)時(shí)，第 i 層需要修改的節(jié)點(diǎn)為 p，也就是位于查找路徑上的節(jié)點(diǎn) 。考慮以下示例，我們想要在其中插入值 17，設(shè)隨機(jī)層數(shù)為 randomLevel() == 2 ，update[] 函數(shù)就包含兩個(gè)元素，update[1] 存儲(chǔ)的是 key 為 9 的結(jié)點(diǎn)的地址，update[0] 存儲(chǔ)的是值為 12 的結(jié)點(diǎn)的地址，當(dāng)插入值 17 之后，9 和 12 的前向結(jié)點(diǎn)就變成了 17 ，而 17 的前向結(jié)點(diǎn)就變成了**9** 和 12 原始的前向結(jié) 25 和 19 。

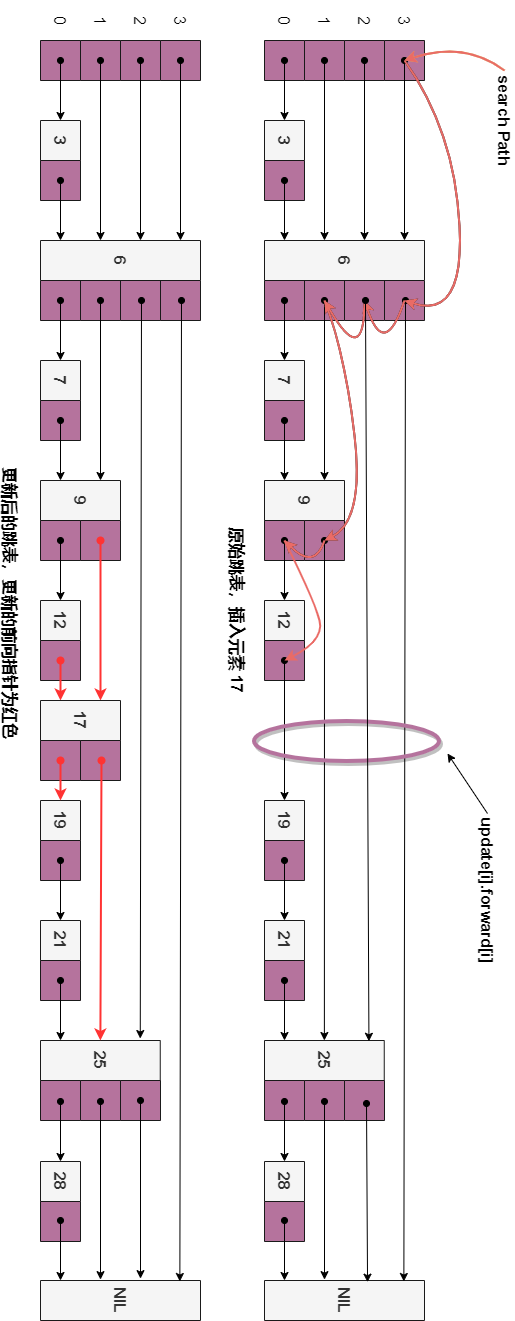
跳表的查找操作

跳表的查找操縱非常類(lèi)似于在跳表插入操作中搜索插入元素的位置的方法。基本的想法是：

下一個(gè)節(jié)點(diǎn)的關(guān)鍵字 key 小于查找的關(guān)鍵字，則我們?cè)谕粚由侠^續(xù)前進(jìn)查找。
下一個(gè)節(jié)點(diǎn)的關(guān)鍵字 key 大于查找的關(guān)鍵字，則我們將指向當(dāng)前節(jié)點(diǎn)i的指針存儲(chǔ)在 update[i] 處，并向下移動(dòng)一層，繼續(xù)搜索。

在最底層（第 0 層），如果最右邊元素的前向元素的值等于搜索關(guān)鍵字的值，則我們找到了關(guān)鍵字，否則未找到。

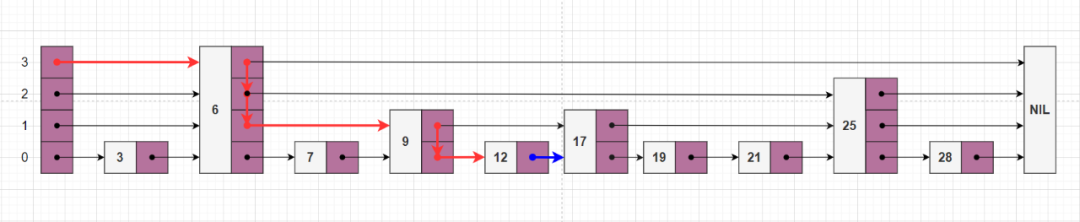
如圖所示，查找關(guān)鍵字 17 ，紅色的路線表示查找路徑，其中的藍(lán)色箭頭表示最右邊元素 12 的前向指針，該指針的值 17 與查找的關(guān)鍵字 key 相等，返回值為 key 的結(jié)點(diǎn)。

實(shí)現(xiàn)代碼相當(dāng)簡(jiǎn)單了：

public Node search(int key) {
    Node current = head;
    for (int i = currentLevel - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < value) {
            current = current.forwards[i];
        }
    }
    // current.key = 12
    if (current.forwards[0] != null && current.forwards[0].key == key) {
        return current.forwards[0];
    } else {
        return null;
    }
}

其中 currentLevel 表示當(dāng)前跳表的層數(shù)，如上圖中的 currentLevel = 4 。

跳表的刪除操作

在刪除元素 key 之前，使用上述查找方法在跳表中定位元素。如果找到了元素，就像我們?cè)趩捂湵碇兴龅哪菢樱匦屡帕兄羔樢詣h除列表中的元素。

我們從最底層（第 0 層）開(kāi)始向上重新排列，直到 update[i] 的下一個(gè)元素不是 key 。刪除元素后，可能會(huì)導(dǎo)致跳表層數(shù) currentLevel 的降低，最后對(duì)其進(jìn)行更新即可。

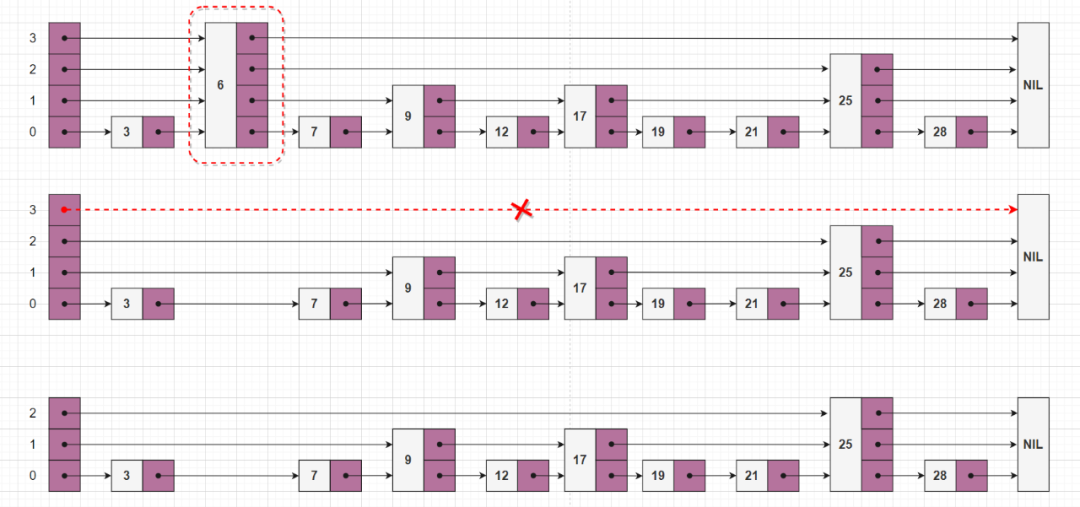
如上圖所示，刪除 key = 6 的結(jié)點(diǎn)之后，第三層沒(méi)有了元素(紅色虛線箭頭)。所以我們將跳表的層數(shù)減 1。

public void delete(int key) {
    Node[] update = new Node[currentLevel];
    Node current = head;
    // 查找要?jiǎng)h除結(jié)點(diǎn)的前序結(jié)點(diǎn)并保存至 update[] 中
    for (int i = currentLevel - 1; i >= 0; --i) {
        while (current.forwards[i] != null && current.forwards[i].key < key) {
            current = current.forwards[i];
        }
        update[i] = current;
    }
    // 將 update[] 的前向結(jié)點(diǎn)設(shè)置為要?jiǎng)h除結(jié)點(diǎn)的forwords[i]
    if (current.forwards[0] != null && current.forwards[0].key == key) {
        for (int i = currentLevel - 1; i >= 0; --i) {
            if (update[i].forwards[i] != null && update[i].forwards[i].data == key) {
                update[i].forwards[i] = update[i].forwards[i].forwards[i];
            }
        }
    }
    // 更新跳表的層數(shù)
    while (currentLevel > 1 && head.forwards[currentLevel] == null) {
        currentLevel--;
    }
}

復(fù)雜度分析

空間復(fù)雜度

跳表的 期望空間復(fù)雜度 為。

在最壞的情況下，每一層有序鏈表等于初始有序鏈表，即跳表的 最差空間復(fù)雜度 為。

時(shí)間復(fù)雜度

跳表的查找、插入和刪除操作的時(shí)間復(fù)雜度均取決于查找的時(shí)間，查找的 最壞時(shí)間復(fù)雜 為。

平均時(shí)間復(fù)雜度 為。大家就當(dāng)二分查找。

當(dāng)然按照論文中的證明，沒(méi)有這么簡(jiǎn)單了。

跳表的應(yīng)用

適用場(chǎng)景：節(jié)點(diǎn)插入和刪除操作比較少，查詢頻次較多的情況。

使用跳表的產(chǎn)品：

Lucene, elasticSearch
Redis：Redis sorted set的內(nèi)部使用 HashMap 和跳表(SkipList)來(lái)保證數(shù)據(jù)的存儲(chǔ)和有序，HashMap 里放的是成員到 score 的映射，而跳躍表里存放的是所有的成員，排序依據(jù)是 HashMap 里存的 score ，使用跳表的結(jié)構(gòu)可以獲得比較高的查找效率，并且在實(shí)現(xiàn)上比較簡(jiǎn)單。
HBase MemStore 內(nèi)部數(shù)據(jù)存儲(chǔ)


推薦閱讀
國(guó)產(chǎn)小眾瀏覽器因屏蔽視頻廣告，被索賠100萬(wàn)（后續(xù)）
年輕人“不講武德”：因看黃片上癮，把網(wǎng)站和786名女主播起訴了
中國(guó)聯(lián)通官網(wǎng)被發(fā)現(xiàn)含木馬腳本，可向用戶推廣色情APP
張一鳴：每個(gè)逆襲的年輕人，都具備的底層能力

關(guān)于程序員大白

程序員大白是一群哈工大，東北大學(xué)，西湖大學(xué)和上海交通大學(xué)的碩士博士運(yùn)營(yíng)維護(hù)的號(hào)，大家樂(lè)于分享高質(zhì)量文章，喜歡總結(jié)知識(shí)，歡迎關(guān)注[程序員大白]，大家一起學(xué)習(xí)進(jìn)步！

圖解：什么是跳表？