圖解:什么是并查集?
點擊上方“程序員大白”,選擇“星標”公眾號
重磅干貨,第一時間送達
Uion-Find 算法
在計算機科學中,并查集(英文:Disjoint-set data structure,直譯為不交集數(shù)據(jù)結構)是一種數(shù)據(jù)結構,用于處理一些不交集(Disjoint sets,一系列沒有重復元素的集合)的合并及查詢問題。并查集支持如下操作:
查詢:查詢某個元素屬于哪個集合,通常是返回集合內(nèi)的一個“代表元素”。這個操作是為了判斷兩個元素是否在同一個集合之中。 合并:將兩個集合合并為一個。 添加:添加一個新集合,其中有一個新元素。添加操作不如查詢和合并操作重要,常常被忽略。
由于支持查詢和合并這兩種操作,并查集在英文中也被稱為聯(lián)合-查找數(shù)據(jù)結構(Union-find data structure)或者合并-查找集合(Merge-find set)。
并查集是用于計算最小生成樹的迪杰斯特拉算法中的關鍵。由于最小生成樹在網(wǎng)絡路由等場景下十分重要,并查集也得到了廣泛的引用。此外,并查集在符號計算,寄存器分配等方面也有應用。
引論
設計一個算法大致分為六個步驟:
定義問題(define the problem) 設計一個算法來解決問題(Find an algorithm to solve it) 判斷算法是否足夠高效?(Fast Enough?) 如果不夠高效,思考為什么,并進行優(yōu)化。(If not,figure out why ?) 尋找一種方式來處理問題 (Find a way to address the problem) 迭代設計,直到滿足條件 (Iterate until satisfied.)
我們從一個基本問題:網(wǎng)絡連通性(Network connectivity)出發(fā),該問題可以抽象為:
一組對象。 UNION 命令:連接兩個對象。 FIND 查詢:是否有路徑將一個對象連接到另一個對象?

并查集的對象可以是下面列出的任何類型:
網(wǎng)絡中的計算機 互聯(lián)網(wǎng)上的 web 頁面 計算機芯片中的晶體管。 變量名稱別名。 數(shù)碼照片中的像素。 復合系統(tǒng)中的金屬點位。

圖 1 連通圖
在編程的時候,為了方便起見,我們對這些對象從 0 到 n-1 進行編號,從而用一個整形數(shù)字表示對象。隱藏與 Union-find 不相關的細節(jié);可以使用整數(shù)快速獲取與對象相關的信息(數(shù)組的下標);可以使用符號表對對象進行轉化。
簡化有助于我們理解連通性的本質。
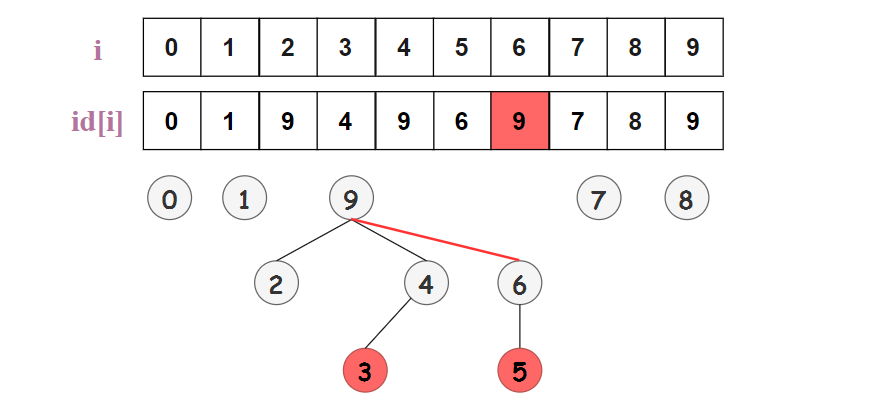
如圖 1 所示,假設我們有編號為 [0,1,2,3,4,5,6,7,8,9] 的 10 個對象,對象的不相交集合為 : {{0},{1},{2,3,9},{5,6},{7},{4,8}} 。
Find 查詢:2 和 9 是否在一個集合當中呢?
答:{{0},{1},{2,3,9},{5,6},{7},{4,8}} 。
Union 命令:合并包含 3 和 8 的集合。
答:{{0},{1},{2,3,4,8,9},{5,6},{7}} 。
連接組件(Connected Component):一組相互連接的頂點.
每一次 Union 命令會將組(連通分量)的數(shù)量減少 1 個。
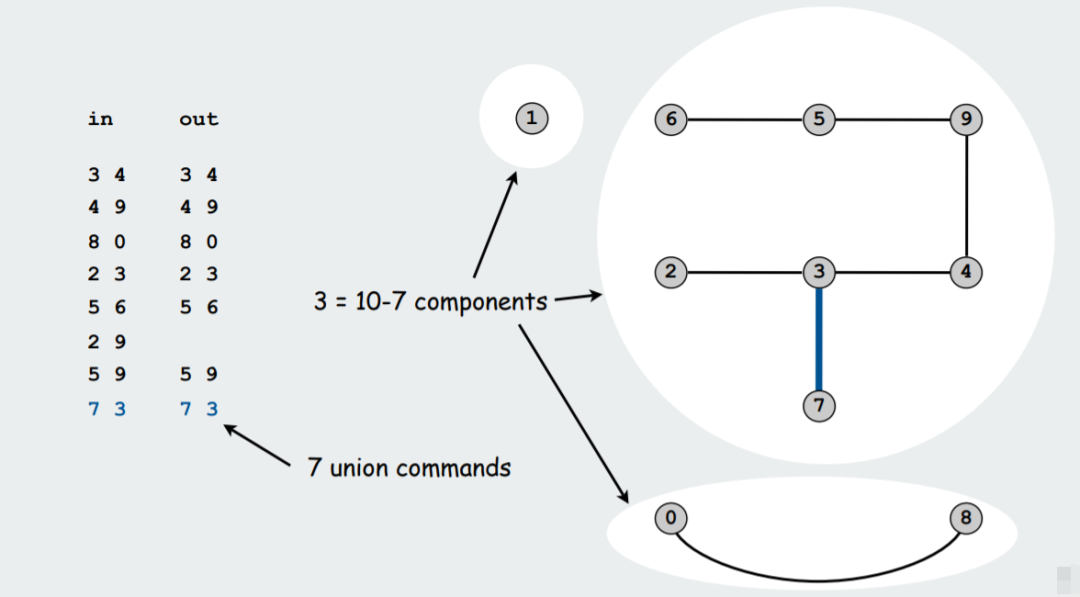
如上圖所示,初始時,每一個頂點為一個組,我們執(zhí)行了 7 次 Union 操作后,變成了 3 個組。其中 {2 9} 不算做一次 Union 操作,是因為在 Union 之前,我們使用 Find 查找命令,會發(fā)現(xiàn) {2 9} 此時已經(jīng)位于同一個組 {2 3 4 5 6 9} 當中。
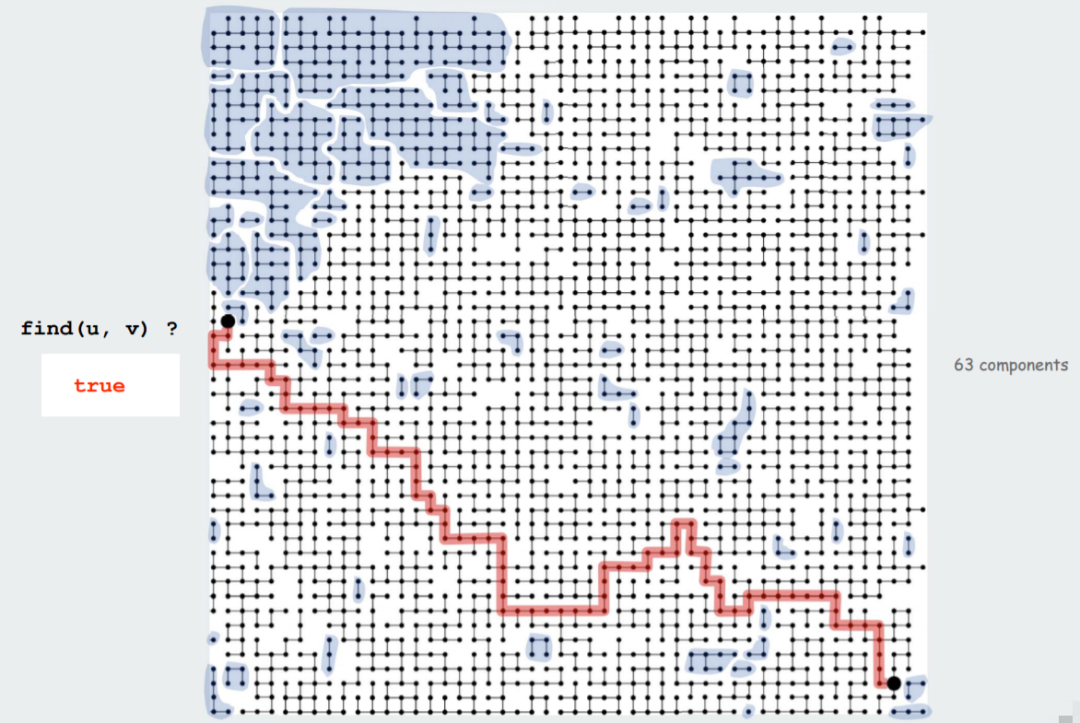
以網(wǎng)絡連通性問題為例,如下圖所示,find(u,v) 可以判斷頂點 u 和 v 是否聯(lián)通?

如下圖所示,圖中共包含 63 個組,其中對象 u 和 對象 v 在同一個集合當中,我們可以找到一條從對象 u 到對象 v 的路徑(紅色路線)但是我們并不關心這條路勁本身,只關心他們是否聯(lián)通:
上面的問題看似很復雜,但也很容易抽象為 Union-Find 模型:
對象。 對象的不相交集(Disjoint Set)。 Find 查詢:兩個對象是否在同一集合中? Union 命令:將包含兩個對象的集合替換為它們的并集。
現(xiàn)在目標就是為 Union-Find 設計一個高效的數(shù)據(jù)結構:
Find 查詢和 Union 命令可以混合使用。 Find 和 Union 的操作數(shù)量 M 可能很大。 對象數(shù)量 N 可能很大。
Quick-Find
設計一個大小為 N 的整型數(shù)組 id[],如果 p 和 q 有相同的 id ,即 id[p] = id[q],則認為 p 和 q 是聯(lián)通的,位于同一個集合中,如下圖所示,5 和 6 是聯(lián)通的,2、3、4 和 9 是聯(lián)通的。

Find(p,q) 查詢操作只需要判斷 p 和 q 是否具有相同的 id,即 id[p] 是否等于 id[q] ;比如查詢 Find(2,9),id[2] = id[9] = 9 ,則 2 和 9 是聯(lián)通的。
Union(p,q) 操作:合并包含 p 和 q 的所有組,將輸入中所有 id 為 id[p] 的對象 id 修改為 id[q]。比如 Union(3,6) ,需要將 id 為 id[3] = 9 的所有對象 {2,3,4,9} 的 id 均修改為 id[6] = 6 ,如下圖所示。
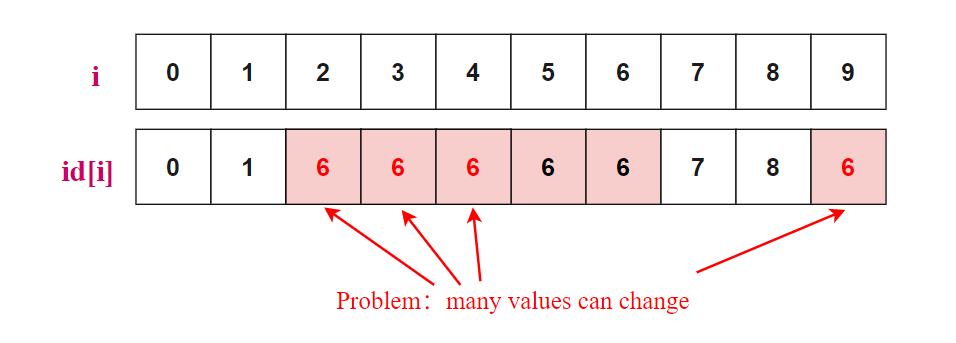
Find(u,v) 的時間復雜度為 ,Union(p,q) 的時間復雜度為 量級 ,每一次 Union 操作需要更新很多元素 i 的 index id[i] 。
以下圖為例,我們依次執(zhí)行 Union(3,4), Union(4,9), Union(8,0), Union(2,3),......,Union(6,1) 操作,整形數(shù)組 id[] 中元素的變化過程。

實現(xiàn)
public class QuickFind
{
private int[] id;
public QuickFind(int N)
{
id = new int[N];
for (int i = 0; i < N; i++){
id[i] = i;
}
}
public boolean find(int p, int q)
{
return id[p] == id[q];
}
public void unite(int p, int q)
{
int pid = id[p];
for (int i = 0; i < id.length; i++) {
if (id[i] == pid) {
id[i] = id[q];
}
}
}
}
復雜度分析
Quick-find 算法的 find 函數(shù)非常簡單,只是判斷 id[p] == id[q] 并返回,時間復雜度為 ,而 Union(u,v) 函數(shù)因為無法確定誰的 ID 與 id[q] 相同,所以每次都要把整個數(shù)組遍歷一遍,如果一共有 個對象,則時間復雜度為 。綜合一下,表示如果 Union 操作執(zhí)行 次,總共 個對象(數(shù)組大小),則時間復雜度為 量級,。
因為這個算法 Find 操作很快,而 Union 操作卻很慢,所以將其稱為 Quick-Find 算法。
Quick-Union
回憶 Quick-Find 中 union 函數(shù),就像是暴力法,遍歷所有對象的 id[] ,然后把有著相同 id 的數(shù)全部改掉, Quick-Union 算法則是引入 “樹” 的概念來優(yōu)化 union 函數(shù),我們把每一個數(shù)的 id 看做是它的父結點。比如說,id[3] = 4,就表示 3 的父結點為 4。
與 Quick-Find 算法使用一樣的數(shù)據(jù)結構,但是 id[] 數(shù)組具有不同的含義:
大小為 的整型數(shù)組 id[]解釋: id[i]表示i的父結點i的根結點為id[id[id[...id[i]...]]]
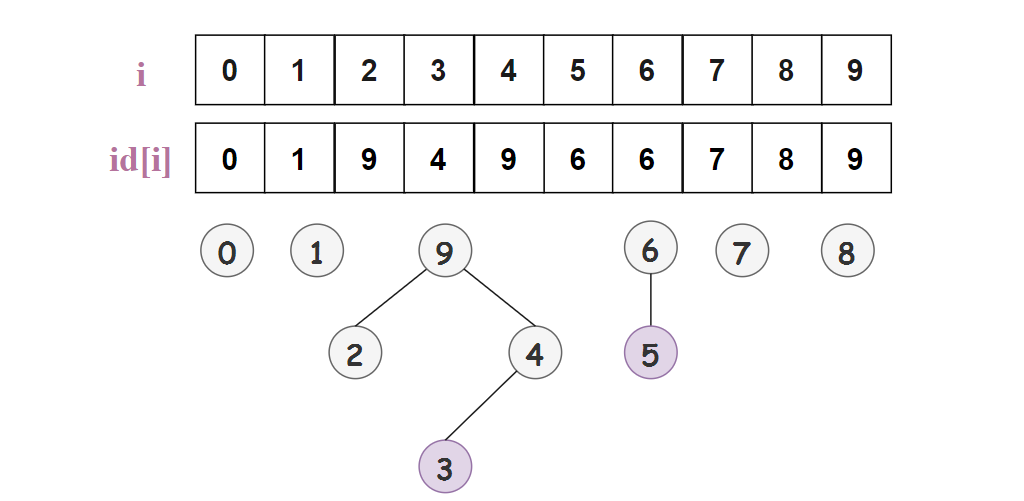
如圖所示,id[2] = 9 就表示 2 的父結點為 9;3 的根節(jié)點為 9 (3 的父結點為 4,4 的父結點為 9,9的父結點還是 9,也就是根結點了),5 的根結點為 6 。
那么 Find(p,q) 操作就變成了判斷 p 和 q 的根結點是否相同,比如 Find(2,3) ,2 和 3 的根結點 9 相同,所以 2 和 3 是聯(lián)通的。
Union(p,q) 操作就是將 q 根結點的 id 設置為 p 的根結點的 id。如上圖所示,Union(3,5) 就是將 5 的根結點的 6 設置為 3 的根結點 9 ,即 id[5] = 9 ,僅更新一個元素的 id 。
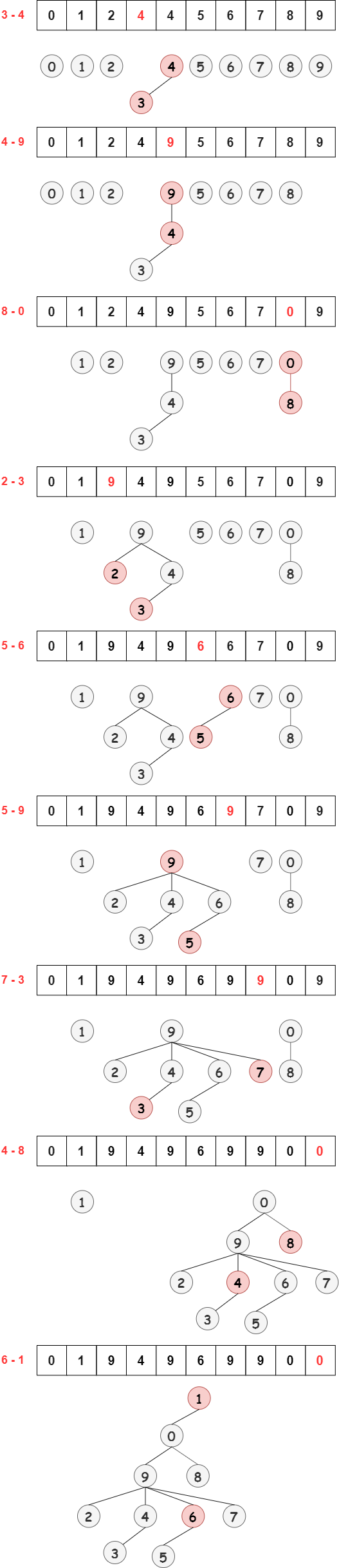
對于原數(shù)組 i = {0,1,2,3,4,5,6,7,8,9} 及 id 數(shù)組 id[10] = {0,1,2,3,4,5,6,7,8,9} ,依次執(zhí)行 Union(3,4) ,Union(4,9) ,Union(8,0) ,Union(2,3) ,Union(5,6) ,Union(5,9) ,Union(7,3) ,Union(4,8) ,Union(6,2) 的過程中如下:
實現(xiàn)代碼
public class QuickUnion
{
private int[] id;
public QuickUnion(int N) {
id = new int[N];
for (int i = 0; i < N; i++) id[i] = i;
}
private int root(int i) {
while (i != id[i]) i = id[i];
return i;
}
public boolean find(int p, int q) {
return root(p) == root(q);
}
public void unite(int p, int q) {
int i = root(p);
int j = root(q);
id[i] = j;
}
}
復雜度分析
對于 Find(p,q) 操作,只需要找到 p 的根結點和 q 的根結點,檢查它們是否相等。合并操作就是找到兩個根節(jié)點并將第一個根節(jié)點的 id 記錄值設為第二個根節(jié)點 。
與 Quick-Find 算法相比, Quick-Union 算法對于問題規(guī)模較大時是更加高效。不幸的是,Quick-Union 算法快了一些但是依然太慢了,相對 Quick-Find 的慢,它是另一種慢。有些情況下它可以很快,而有些情況下它還是太慢了。但 Quick-Union 算法依然是用來求解動態(tài)連通性問題的一個快速而優(yōu)雅的設計。
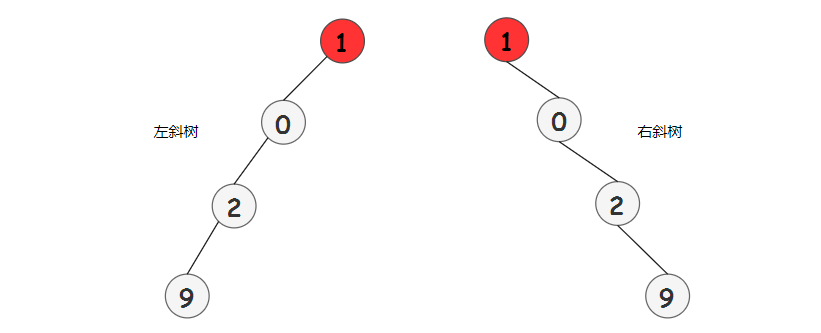
Quick-Union 算法的缺點在于樹可能太高了。這意味著查找操作的代價太大了。你可能需要回溯一棵瘦長的樹(斜樹),每個對象只是指向下一個節(jié)點,那么對葉子節(jié)點執(zhí)行一次查找操作,需要回溯整棵樹,只進行查找操作就需要花費 N 次數(shù)組訪問,如果操作次數(shù)很多的話這就太慢了。
Find 操作:最好時間復雜度為 ,最壞為 ,平均 。
Union 操作:最好時間復雜度為 ,最壞為 ,平均
當進行 次 Union 操作,那么平均時間復雜度就是 。
Weighted Quick-Union
好,我們已經(jīng)看了快速合并和快速查找算法,兩種算法都很容易實現(xiàn),但是不支持巨大的動態(tài)連通性問題。那么,我們該怎么改進呢?
一種非常有效的改進方法,叫做加權。也許我們在學習前面兩個算法的時候你已經(jīng)想到了。這個改進的想法是在實現(xiàn) Quick-Union 算法的時候執(zhí)行一些操作避免得到一顆很高的樹。
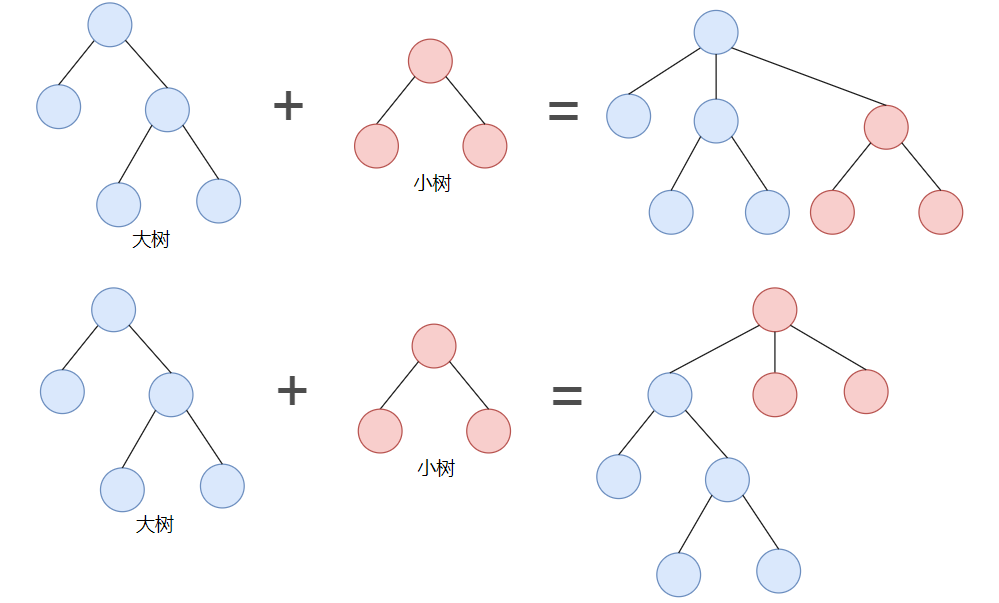
如果一棵大樹和一棵小樹合并,避免將大樹放在小樹的下面,就可以一定程度上避免更高的樹,這個加權操作實現(xiàn)起來也相對容易。我們可以跟蹤每棵樹中對象的個數(shù),然后我們通過確保將小樹的根節(jié)點作為大樹的根節(jié)點的子節(jié)點以維持平衡,所以,我們避免將大樹放在小樹下面的情況。
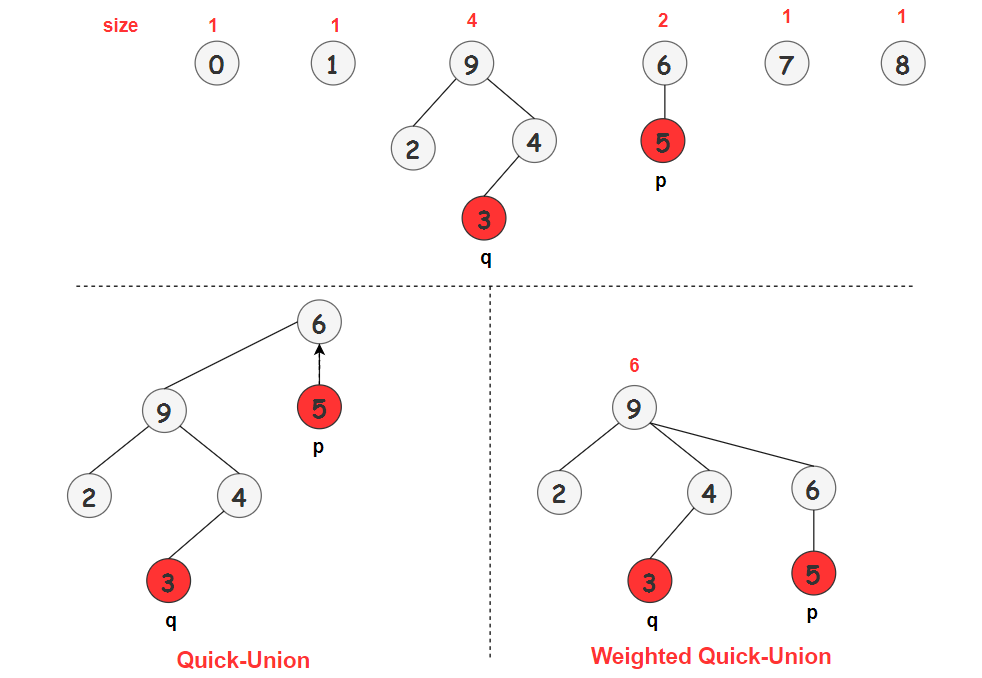
如上圖所示,以 Union(5,3) 為例,5 的根結點為 6,3 的根結點為 9 :
Quick-Union:以 9 為根結點樹將作為 6 的子樹 Weighted Quick-Union:以 6 為根結點的樹將作為 9 的子樹。
我們可以看一下 Weighted Quick-Union 操作的例子:

可以看到 Weighted Quick-Union 所生成的樹很 “胖”,剛好滿足我們的需求。
實現(xiàn)代碼
Weighted Quick-Union 的實現(xiàn)基本和 Quick-Union 一樣,我們只需要維護一個數(shù)組 sz[] ,用來保存以 i 為根的樹中的對象個數(shù),比如 sz[0] = 1 ,就表示以 0 為根的樹包含 1 個對象。
public class WeightedQuickUnion
{
private int[] id;
private int[] sz;
public WeightedQuickUnion(int N) {
id = new int[N];
sz = new int[N];
for (int i = 0; i < N; i++) {
id[i] = i;
sz[i] = 1; // 初始時,每一個結點為一棵樹,sz[i] = 1
}
}
private int root(int i) {
while (i != id[i]) i = id[i];
return i;
}
public boolean find(int p, int q) {
return root(p) == root(q);
}
public void unite(int p, int q) {
int i = root(p);
int j = root(q);
if (sz[i] < sz[j]) {
id[i] = j;
sz[j] += sz[i];
} else {
id[j] = i;
sz[i] += sz[j];
}
}
}
復雜度分析
對于加權 Quick-Union 算法處理 個對象和 條連接時最多訪問 次,其中 為常數(shù),即時間復雜度為 量級。與 Quick-Find 算法(以及某些情況下的 Quick-Union 算法)的時間復雜度 形成鮮明對比。
Find 操作:
Union 操作:
Union-Find
Union-Find 算法是在 Weighted Quick-Union 的基礎之上進一步優(yōu)化,即路徑壓縮的 Weighted Quick-Union 算法。Weighted Quick-Union 算法通過對 Union 操作進行加權保證 Quick-Union 算法可能出現(xiàn)的 “瘦高” 情況發(fā)生。而 Union-Find 算法是通過路徑壓縮進一步將 Weighted Quick-Union 算法的樹高降低。
所謂 路徑壓縮 ,就是在計算結點 i 的根之后,將回溯路徑上的每個被檢查結點的 id 設置為**root(i)**。
如下圖所示,root(9)=0 ,從結點 9 到根結點 0 的路徑為 9→6→3→1→0 ,則將 6,3,1 的根結點設置為 0 。這樣一來,樹的高度一下子就變矮了,而且對于 Union 和 Find 操作沒有任何影響。
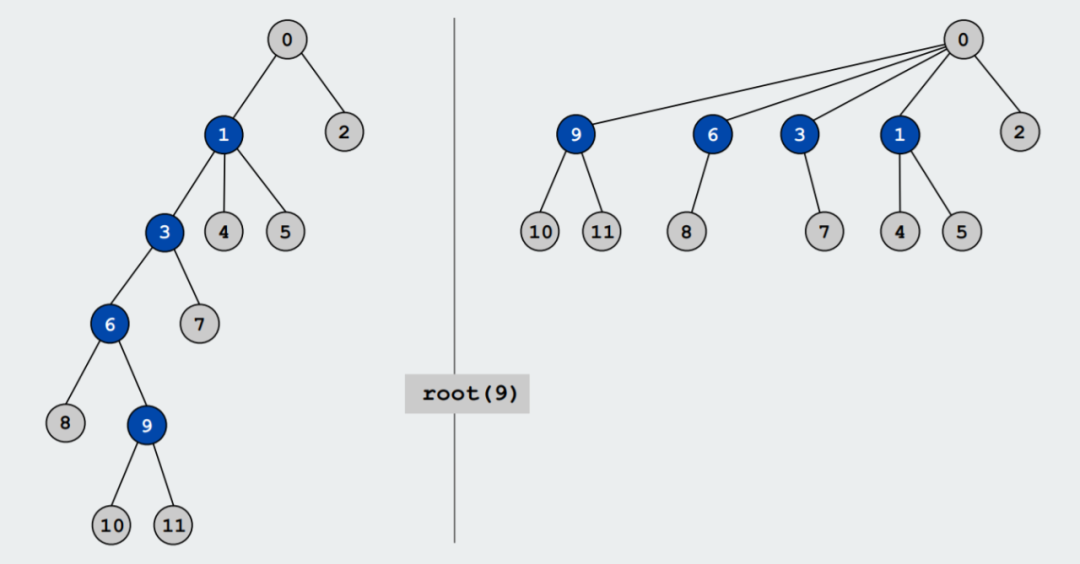
路徑壓縮:
標準實現(xiàn):在 root()中添加第二個循環(huán),將每個被遍歷到的結點的的 id 設置為根結點。
private int root(int i) {
int root = i;
// 找到結點 i 的根結點 root
while (root != id[root]) root = id[root];
// 每個被遍歷到的結點的的 id 設置為根結點 root
while (i != root) {
int tmp = id[i];
id[i] = root;
i = tmp;
}
return root;
}
簡化的實現(xiàn):使路徑中的所有其他結點指向其祖父結點,即 id[i] = id[id[i]]。
private int root(int i) {
while (i != id[i]) {
id[i] = id[id[i]]; // 簡化的方法
i = id[i];
}
return i;
}
在實踐中,我們沒有理由不選擇簡化的方式,簡化的方式同樣可以使樹幾乎完全平坦,如下圖所示:

復雜度分析
定理:從一個空數(shù)據(jù)結構開始,對 個對象執(zhí)行 次 Union 和 Find 操作的任何序列都需要 時間。時間復雜度的具體證明非常困難,但這并不妨礙算法的簡單性!
路徑壓縮的加權 Quick-Union (Weigthed Quick-Union with Path Compression)算法雖是最優(yōu)算法,但是并非所有操作都能在常數(shù)時間內(nèi)完成。也就是,WQUPC 算法的每個操作在最壞情況下(即均攤后)都不是常數(shù)級別的,而且不存在其他算法能夠保證 Union-Find 算法的所有操作在均攤后都是常數(shù)級別。
各類算法時間復雜度對比
| 算法 | Union | Find | 最壞時間復雜度 |
|---|---|---|---|
| Quick-Find | N | 1 | MN |
| Quick-Union | tree Height | tree Height | MN |
| Weighted Quick-Union | lg N | lg N | N+MlogN |
| WQUPC | Very near to 1 (amortized) | Very near to 1 (amortized) | (N+M)logN |
對于大規(guī)模的數(shù)據(jù),比如包含 個頂點, 條邊的圖,WQUPC 可以將時間從 3000 年降低到 1 分鐘之內(nèi)就可以處理完,而這是超級計算機也無法匹敵的。對于同一問題,使用一部手機運行的 WQUPC 輕松擊敗在超級計算機 上運行的Quick-Find 算法,這也許就是算法的魅力。
并查集的應用
網(wǎng)絡連通性問題 滲濾 圖像處理。 最近公共祖先。 有限狀態(tài)自動機的等價性。 Hinley-Milner 的多態(tài)類型推斷。 Kruskal 的最小生成樹算法。 游戲(圍棋、十六進制)。 在 Fortran 中的編譯語句的等價性問題
推薦閱讀
國產(chǎn)小眾瀏覽器因屏蔽視頻廣告,被索賠100萬(后續(xù))
年輕人“不講武德”:因看黃片上癮,把網(wǎng)站和786名女主播起訴了
關于程序員大白
程序員大白是一群哈工大,東北大學,西湖大學和上海交通大學的碩士博士運營維護的號,大家樂于分享高質量文章,喜歡總結知識,歡迎關注[程序員大白],大家一起學習進步!


