圖解:什么是哈希?
為什么要有哈希?
假設(shè)我們要設(shè)計(jì)一個(gè)系統(tǒng)來(lái)存儲(chǔ)將員工手機(jī)號(hào)作為主鍵的員工記錄,并希望高效地執(zhí)行以下操作:
插入電話號(hào)碼和相應(yīng)的信息。(插入) 搜索電話號(hào)碼并獲取信息。(查找) 刪除電話號(hào)碼及相關(guān)信息。(刪除)
我們可以考慮使用以下數(shù)據(jù)結(jié)構(gòu)來(lái)維護(hù)不同電話所對(duì)應(yīng)的信息:
數(shù)組 鏈表 平衡二叉樹(紅黑樹等等) 直接訪問(wèn)表
對(duì)于數(shù)組和鏈表而言,我們需要以線性的方式進(jìn)行查找,這在實(shí)際應(yīng)用中代價(jià)太大;如果我們使用數(shù)組且保證數(shù)組中電話號(hào)碼有序排列,那么使用二分查找可將查找電話號(hào)碼的時(shí)間復(fù)雜度降到 ,但同時(shí)由于要維持?jǐn)?shù)組的有序性,插入和刪除操作的代價(jià)將變大 。
對(duì)于平衡二叉查找樹而言,插入、查找和刪除操作的時(shí)間復(fù)雜度均為 ,這似乎已經(jīng)看著很不錯(cuò)了,那么是否有更好的數(shù)據(jù)結(jié)構(gòu)呢?
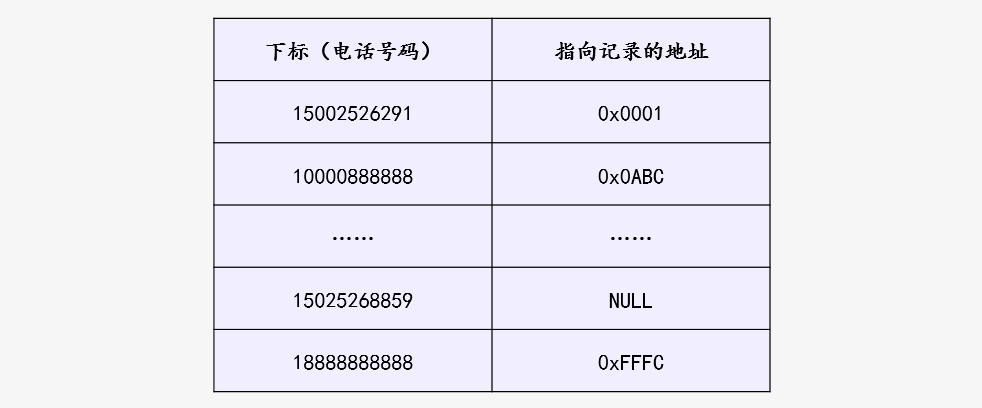
再來(lái)看直接訪問(wèn)表的方式,首先創(chuàng)建一個(gè)大數(shù)組(至少能夠用電話號(hào)碼作為數(shù)組下標(biāo)),如果電話號(hào)碼沒(méi)有出現(xiàn)在數(shù)組當(dāng)中,就在相應(yīng)下標(biāo)填充 NULL ;如果電話號(hào)碼出現(xiàn)了,則下標(biāo)中數(shù)據(jù)填充該電話號(hào)碼關(guān)聯(lián)的記錄的地址。
這樣一來(lái),插入、查找和刪除的時(shí)間復(fù)雜度將降為 ,比如插入一條記錄(15002629900,0xFF0A “可愛(ài)的讀者”),只需要將手機(jī)號(hào)碼 15002629900 當(dāng)做下標(biāo),然后在該下標(biāo)的位置填充記錄的地址,即 arr[15002629900] = 0xFF0A;
但是直接訪問(wèn)表有實(shí)踐上的限制。首先需要申請(qǐng)額外的存儲(chǔ)空間,并且存在大量的空間浪費(fèi)。比如對(duì)于一個(gè)含有 n 位的電話號(hào)碼,我們需要 的空間復(fù)雜度,其中 m 表示數(shù)據(jù)本身所占用的空間。另外一個(gè)問(wèn)題是,編程語(yǔ)言本身提供的整型無(wú)法表示電話號(hào)碼。
由于上述限制,使用直接訪問(wèn)表并不是最明智的方法。而哈希則是解決以上問(wèn)題的最好數(shù)據(jù)結(jié)構(gòu),并且與上面所提到的數(shù)據(jù)結(jié)構(gòu)(數(shù)組,鏈表,AVL樹)在實(shí)踐中相比,性能非常好。通過(guò)哈希,可以在 的時(shí)間復(fù)雜度內(nèi)實(shí)現(xiàn)插入、查找和刪除操作(在合理的假設(shè)下),最壞情況下為 的時(shí)間復(fù)雜度。
哈希是對(duì)直接訪問(wèn)表的改進(jìn)。使用哈希函數(shù)將給定的電話號(hào)碼或任何其他鍵轉(zhuǎn)換為較小的數(shù)字,將該較小的數(shù)字稱為哈希表的索引(哈希值)
什么是哈希表?
哈希表和直接訪問(wèn)表很類似,同樣是一個(gè)用于存儲(chǔ)指向給定電話號(hào)碼對(duì)應(yīng)記錄的指針的數(shù)組,只不過(guò),此時(shí)的數(shù)組下標(biāo)不再是電話號(hào)碼,而是經(jīng)過(guò)哈希函數(shù)映射后的輸出值。
什么是哈希函數(shù)?
哈希函數(shù)用于將一個(gè)大數(shù)(手機(jī)號(hào)碼)或字符串映射為一個(gè)可以作為哈希表索引的較小整數(shù)的函數(shù)。比如活動(dòng)開發(fā)中經(jīng)常使用的 MD5 和 SHA 都是歷史悠久的Hash算法。
[lovefxs@localhost?~]$?echo?-n??"I?love?J"??|?openssl?md5?
(stdin)=?ef821d9b424fd5f0aac7faf029152e04
一個(gè)好的哈希函數(shù)應(yīng)該滿足四個(gè)條件:
執(zhí)行效率要高(效率高)
對(duì)于一段很長(zhǎng)的字符串或者二進(jìn)制文本也能快速計(jì)算出哈希值。
散列結(jié)果應(yīng)當(dāng)具有同一性(輸出值盡量均勻,越均勻沖突就越少)。(同一性)
例如對(duì)于電話號(hào)碼而言,一個(gè)好的哈希函數(shù)應(yīng)該考慮電話號(hào)碼的后四位,而一個(gè)糟糕的哈希算法可能考慮電話號(hào)碼的前四位,因?yàn)楹笏奈桓袇^(qū)分性,相當(dāng)于輸入更加分散,那么輸出也可能更加均勻,當(dāng)然這兩種選擇方式都不是什么好辦法,只是希望大家理解同一性原理。
雪崩效應(yīng)(微小的輸入值變化使得輸出值發(fā)生巨大的變化)。
[lovefxs@localhost?~]$?echo?-n??"I?love?J"??|?openssl?md5?
(stdin)=?ef821d9b424fd5f0aac7faf029152e04
[lovefxs@localhost?~]$?echo?-n??"I?love?Y"??|?openssl?md5?
(stdin)=?fb49af24bebae07658650ae8eb1c0f5b
其中輸入 I love J 和 I love Y 只改變了一個(gè)字母,輸出值卻千差萬(wàn)別。
從哈希函數(shù)的輸出值不可反向推導(dǎo)出原始的數(shù)據(jù)。(不可反向推導(dǎo))
比如上面的原始數(shù)據(jù) I love J ?與經(jīng)過(guò) MD5 算法映射后的輸出值之間沒(méi)有對(duì)應(yīng)關(guān)系。
什么是 Hash 碰撞?
由于哈希函數(shù)的原理是將輸入空間的一個(gè)較大的值映射成 hash 空間內(nèi)一個(gè)較小的值,那么就會(huì)出現(xiàn)兩個(gè)不同的輸入值被映射到了同一個(gè)較小的輸出值。當(dāng)一個(gè)新插入的值被哈希函數(shù)映射到了哈希表中一個(gè)已經(jīng)被占用的槽,就認(rèn)為產(chǎn)生了 Hash 碰撞(沖突)。
那么這種沖突是否可以避免呢?
答案是只能緩解,不可避免。
由于哈希函數(shù)的原理是將輸入空間一個(gè)較大的值映射到一個(gè)較小的 Hash 空間內(nèi),而 Hash空間一般遠(yuǎn)小于輸入的空間。根據(jù)抽屜原理,一定會(huì)存在不同的輸入被映射成同一輸出的情況。
何為抽屜原理?
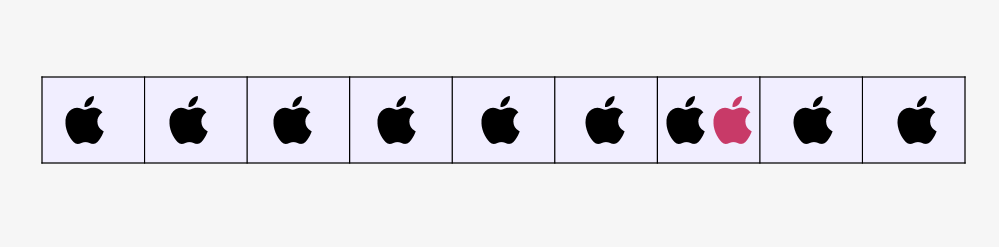
桌上有十個(gè)蘋果,要把這十個(gè)蘋果放到九個(gè)抽屜里,無(wú)論怎樣放,我們會(huì)發(fā)現(xiàn)至少會(huì)有一個(gè)抽屜里面放不少于兩個(gè)蘋果。這一現(xiàn)象就是“抽屜原理”。抽屜原理的一般含義為:“如果每個(gè)抽屜代表一個(gè)集合,每一個(gè)蘋果就可以代表一個(gè)元素,假如有n+1個(gè)元素放到n個(gè)集合中去,其中必定有一個(gè)集合里至少有兩個(gè)元素。” 抽屜原理有時(shí)也被稱為鴿巢原理。它是組合數(shù)學(xué)中一個(gè)重要的原理
知道了為什么哈希碰撞不可避免,那哈希碰撞該如何緩解呢?
Hash 碰撞的解決方案?
鏈地址法 開放地址法 再哈希
鏈地址法
鏈地址法的思想就是將所有發(fā)生碰撞的元素用一個(gè)單鏈表串起來(lái)。
我們以一個(gè)簡(jiǎn)單的哈希函數(shù) H(key) = key MOD 7 (除數(shù)取余法)對(duì)一組元素 [50, 700, 76, 85, 92, 73, 101] 進(jìn)行映射,來(lái)理解鏈地址法處理 Hash 碰撞。
除數(shù)為 7 ,初始化一個(gè)大小為 7 的空 Hash 表:

然后插入元素 50 ,首先對(duì) 50 % 7 = 1 ,得到其哈希值 1 ,在下標(biāo)為 1 的位置插入 50 :

然后計(jì)算 700 % 7 = 0 ,76 % 7 = 6 ,得到的哈希值均未發(fā)生碰撞,填入相應(yīng)位置:

然后計(jì)算 85 % 7 = 1 , 但是下標(biāo)為 1 的位置已經(jīng)有元素 50 ,發(fā)生了碰撞,所以使用單鏈表將 85 和 50 鏈接起來(lái):
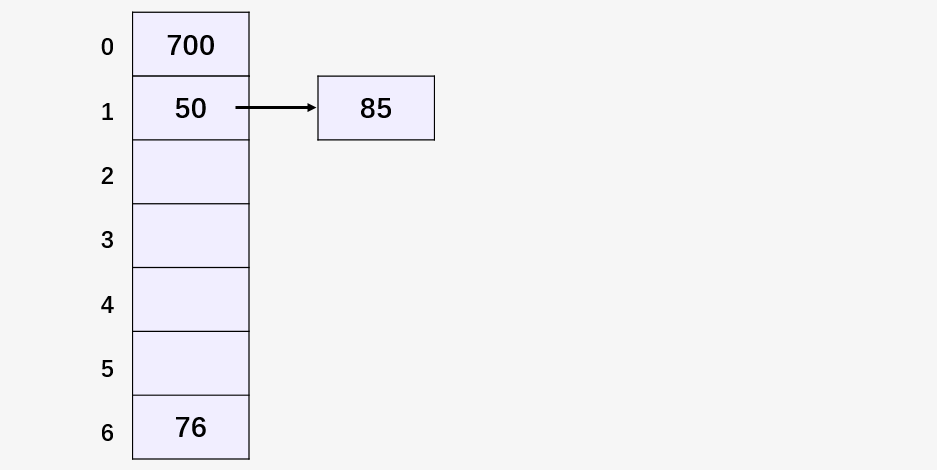
以同樣的方式插入所有元素得到如下的哈希表。鏈地址法解決沖突的方式與圖的鄰接表存儲(chǔ)方式在樣式上很相似,思想還是蠻簡(jiǎn)單,發(fā)生沖突,就用單鏈表組織起來(lái)。
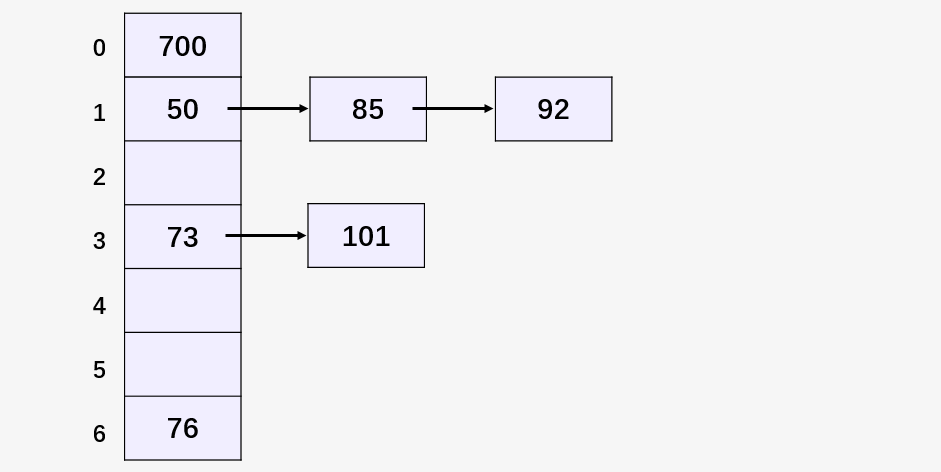
鏈地址法實(shí)現(xiàn)
首先創(chuàng)建一個(gè)空的哈希表,哈希表的表長(zhǎng)為 。
哈希函數(shù):Hash(key) = key % N
插入:計(jì)算要插入關(guān)鍵字 key 的哈希值 Hash(key) ,然后在哈希表中找到對(duì)應(yīng)哈希值的位置,再將 key 插入鏈表的末尾;
刪除:計(jì)算要?jiǎng)h除關(guān)鍵字 key 的哈希值 Hash(key) ,然后在哈希表中找到對(duì)應(yīng)哈希值的位置,再將 key 充鏈表中刪除。
查找:計(jì)算要查找關(guān)鍵字 key 的哈希值 Hash(key) ,然后在哈希表中找到對(duì)應(yīng)哈希值的位置,從該位置開始進(jìn)行單鏈表的線性查找。
using?namespace?std;?
??
class?Hash?
{?
????int?N;????//?哈希表的表長(zhǎng)??
????//?指向?qū)?yīng)存儲(chǔ)下標(biāo)的指針。
????list<int>?*table;?
public:?
????Hash(int?V);?
????void?insertKey(int?x);?
????void?deleteKey(int?key);?????
????int?hashFunction(int?x)?{?
????????return?(x?%?N);?
????}?
??
????void?displayHash();?
};?
??
Hash::Hash(int?b)?
{?
????this->N?=?b;?
????table?=?new?list<int>[N];?
}?
??
void?Hash::insertKey(int?key)?
{?
????int?index?=?hashFunction(key);?
????table[index].push_back(key);??
}?
??
void?Hash::deleteKey(int?key)?
{?
?//計(jì)算key的哈希值?Hash(key)
?int?index?=?hashFunction(key);?
??
????//找到?index
????list?<int>?::?iterator?i;?
????for?(i?=?table[index].begin();?
??????i?!=?table[index].end();?i++)?{?
?????if?(*i?==?key){
???break;?
????????}
??}?
??//如果找到了對(duì)應(yīng)的key,刪除之
??if?(i?!=?table[index].end())?
????table[index].erase(i);?
}?
??
//?輸出哈希表
void?Hash::displayHash()?{?
????for?(int?i?=?0;?i?????????cout?<?????for?(auto?x?:?table[i]){
?????????cout?<"?-->?"?<????????}?
?????cout?<endl;?
????}?
}?
?
int?main()?
{?
????int?a[]?=?{50,?700,?76,?85,?92,?73,?101};?
????int?n?=?sizeof(a)/sizeof(a[0]);?
??
????Hash?h(7);
????for?(int?i?=?0;?i?????????h.insertKey(a[i]);??
????}??
????h.deleteKey(92);?
????h.displayHash();?
??
????return?0;?
}?
鏈地址法的優(yōu)缺點(diǎn):
優(yōu)點(diǎn):
實(shí)現(xiàn)起來(lái)簡(jiǎn)單; 哈希表永遠(yuǎn)不會(huì)溢出,我們可以向單鏈表中添加更多的元素; 對(duì)于哈希函數(shù)和裝填因子(后面會(huì)說(shuō))的選擇沒(méi)啥要求; 在不知道要插入和刪除關(guān)鍵字多少和頻率的情況下,鏈地址法有絕對(duì)優(yōu)勢(shì)。
缺點(diǎn):
由于使用鏈表來(lái)存儲(chǔ)關(guān)鍵字,鏈地址法的緩存性能不佳。開放尋址法使用連續(xù)的地址空間進(jìn)行存儲(chǔ),所以緩存性能更好。 浪費(fèi)空間(因?yàn)楣1淼挠行┪恢脧奈幢皇褂茫?/section> 如果鏈表太長(zhǎng),在最壞的情況下查找的時(shí)間復(fù)雜度將變?yōu)? 。 需要額外的空間存儲(chǔ)鏈表指針。
鏈地址法的性能
假設(shè)任何一個(gè)關(guān)鍵字都以相等的相等的概率被映射到哈希表的任意一個(gè)槽位。
其中 ?表示哈希表的槽位數(shù), 表示插入到哈希表中的關(guān)鍵字的數(shù)目。
裝填因子(load factor) (將 n 個(gè)球隨機(jī)均勻地扔進(jìn) m 個(gè)箱子里的概率)。
期望的查找,插入和刪除的時(shí)間均等于
當(dāng) 為 量級(jí)時(shí),鏈地址法的插入、查找和刪除操作的時(shí)間復(fù)雜度就是 量級(jí)。
極端情況下我們將 n 個(gè)數(shù)都扔進(jìn)了同一個(gè)槽,也就是 n 個(gè)數(shù)形成了一個(gè)單鏈表,那么時(shí)間復(fù)雜度將降為 ,但這個(gè)概率微乎其微。
開放地址法
與鏈地址法一樣,開放地址法也是一個(gè)經(jīng)典的處理沖突的方式。只不過(guò),對(duì)于開放地址法,所有的元素都是存儲(chǔ)在哈希表當(dāng)中的,所以無(wú)論任何時(shí)候都要保證哈希表的槽位數(shù) ?大于或等于關(guān)鍵字的數(shù)目 (必要的時(shí)候,我們還會(huì)復(fù)制舊數(shù)據(jù),然后對(duì)哈希表進(jìn)行動(dòng)態(tài)擴(kuò)容)。
開放地址法分三種方式。
線性探測(cè)法(Linear Probing)
設(shè) Hash(key) 表示關(guān)鍵字 key 的哈希值, 表示哈希表的槽位數(shù)(哈希表的大小)。
線性探測(cè)法則可以表示為:
如果 Hash(x) % M 已經(jīng)有數(shù)據(jù),則嘗試 (Hash(x) + 1) % M ;
如果 (Hash(x) + 1) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 2) % M ;
如果 (Hash(x) + 2) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 3) % M ;
......
我們同樣以哈希函數(shù) H(key) = key MOD 7 (除數(shù)取余法)對(duì) [50, 700, 76, 85, 92, 73, 101] 進(jìn)行映射,來(lái)理解線性探測(cè)法處理 Hash 碰撞。
依次計(jì)算 50 % 7 = 1 、700 % 7 = 0 及 76 % 7 = 6 ,均沒(méi)有發(fā)生沖突(碰撞),則直接放入相應(yīng)的位置:
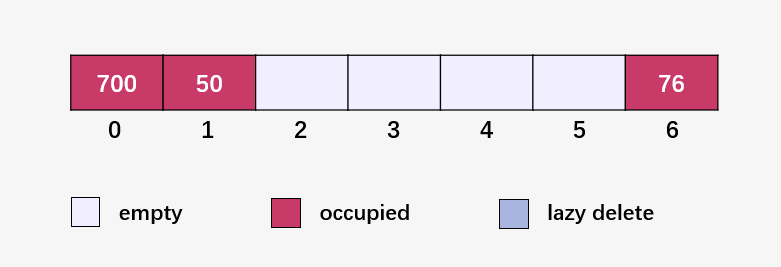
計(jì)算 85 % 7 = 1 ,但是下標(biāo) 1 的位置已經(jīng)有元素 50 ,發(fā)生碰撞,則尋找下一個(gè)可以存放元素 85 的空位 (85 % 7 + 1) % 7 = 2 ,下標(biāo)二沒(méi)有元素,所以將 85 放進(jìn)去:
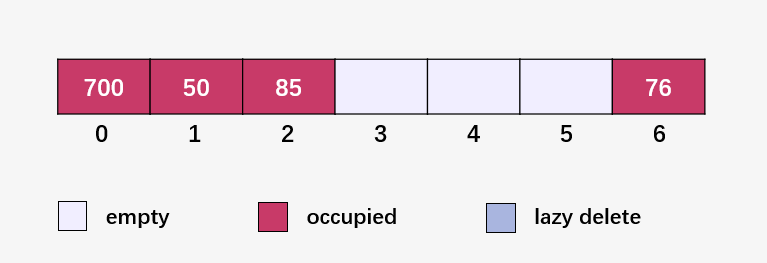
計(jì)算 92 % 7 = 1 ,50 已經(jīng)在 1 的位置,發(fā)生碰撞;線性探測(cè)下一個(gè)位置 (92 % 7 + 1) % 7 = 2 ,85 已經(jīng)在 2 的位置,發(fā)生碰撞;線性探測(cè)下一個(gè)位置 ?(92 % 7 + 2) % 7 = 3 ,此時(shí)為空位,填入 92 :
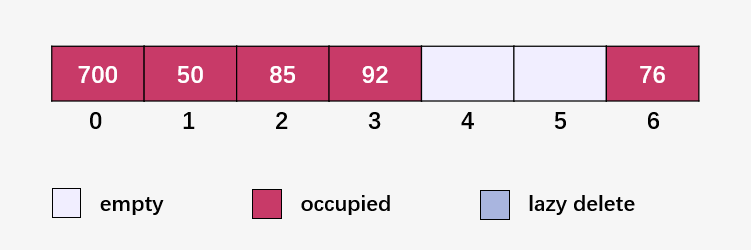
計(jì)算 73 % 7 = 3 ,92 已經(jīng)占用了 3 號(hào)位置,發(fā)生碰撞;線性探測(cè)下一個(gè)位置 (73 % 7 + 1) % 7 = 4 ,此時(shí)為空位,填入 73 :
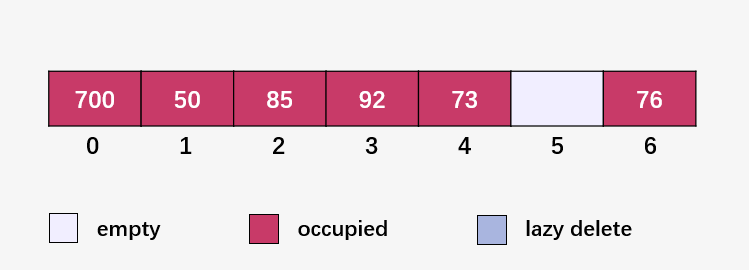
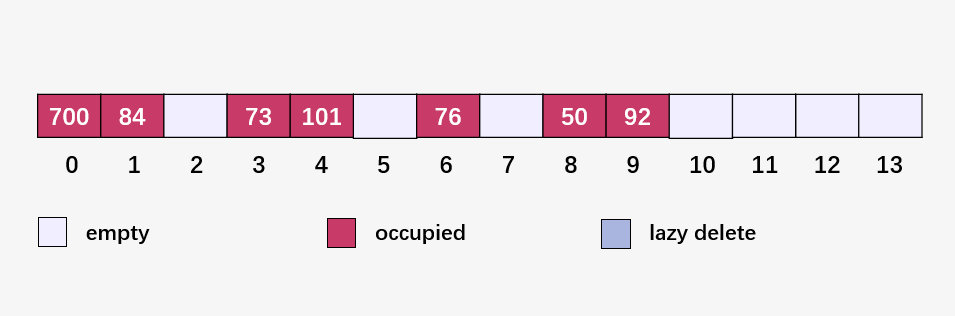
計(jì)算 101 % 7 = 3 , 3 號(hào)位置已經(jīng)有元素,發(fā)生碰撞;線性探測(cè)下一個(gè)位置 (101 % 7 + 1) % 7 = 4 ,4 號(hào)位置已有元素,發(fā)生碰撞;線性探測(cè)下一個(gè)位置 (101 % 7 + 2) % 7 = 5 , 此時(shí)為空,填入 101 :
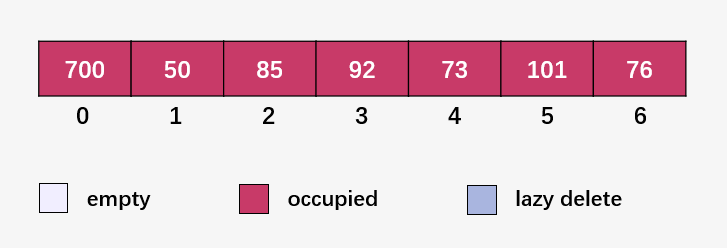
到這里你不難看出線性探測(cè)的缺陷,容易產(chǎn)生聚集(發(fā)生碰撞的元素形成組,比如 [50,85,92,73,101] 之間均是由于碰撞而緊挨著),而且發(fā)生碰撞的情況大大增加,需要花費(fèi)更多的時(shí)間來(lái)尋找空閑的槽位和查找元素。
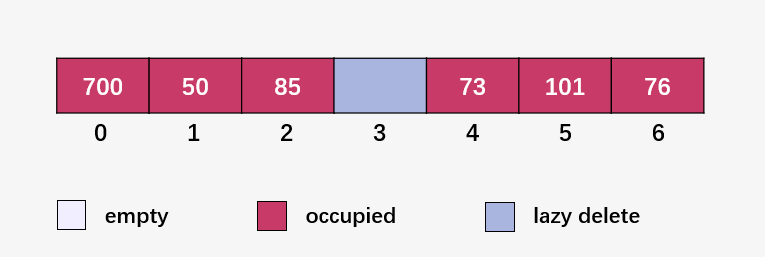
至于(lazy delete)懶刪除就是并不將存儲(chǔ)空間釋放,只是將里面的數(shù)據(jù)清除。
比如刪除元素 92 ,先計(jì)算 92 % 7 = 1 ,但是發(fā)現(xiàn)下標(biāo) 1 是 50,線性向下探測(cè) (92 % 7 + 1) % 7 = 2 ,下標(biāo) 2 為 85,繼續(xù)線性向下探測(cè) (92 % 7 + 2) % 7 = 3 ,發(fā)現(xiàn)下標(biāo) 3 剛好為 92,將該存儲(chǔ)單元的數(shù)據(jù)清空。
平方探測(cè)法(Quadratic Probing)
所謂 Quadratic Probing,就是每次向下探測(cè)的寬度變成了 ,其中的 表示迭代次數(shù)。
設(shè) Hash(key) 表示關(guān)鍵字 key 的哈希值, 表示哈希表的槽位數(shù)(哈希表的大小)。
平方探測(cè)法則可以表示為:
如果 Hash(x) % M 已經(jīng)有數(shù)據(jù),則嘗試 (Hash(x) + 1 * 1) % M ;
如果 (Hash(x) + 1 * 1) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 2 * 2) % M ;
如果 (Hash(x) + 2 * 2) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 3 * 3) % M ;
............
雙重哈希(Double Hashing)
對(duì)于雙重哈希,我們需要一個(gè)新的哈希函數(shù) Hash2(key) ,而且對(duì)于第 i 次迭代探測(cè),我們查找的位置為 i * Hash2(key) .
設(shè) Hash(key) 表示關(guān)鍵字 key 的一個(gè)哈希值, Hash2(key) 表示關(guān)鍵字 key 的另一個(gè)哈希值, 表示哈希表的槽位數(shù)(哈希表的大小)。
雙重哈希探測(cè)法則可以表示為:
如果 Hash(x) % M 已經(jīng)有數(shù)據(jù),則嘗試 (Hash(x) + 1 * Hash2(x)) % M ;
如果 (Hash(x) + 1 * Hash2(x)) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 2 * Hash2(x)) % M ;
如果 (Hash(x) + 2 * Hash2(x)) % M 也有數(shù)據(jù)了,則嘗試 (Hash(x) + 3 * Hash2(x)) % M ;
............
開放地址法的實(shí)現(xiàn)
using?namespace?std;?
??
//?哈希表的大小?
#define?TABLE_SIZE?13?
??
//?用于定義?Hash2(key)
#define?PRIME?7?
class?DoubleHash?{?
????//?定義一個(gè)哈希表?
????int*?hashTable;?//int[]?hashTable;
????int?curr_size;?
??
public:?
????//?判斷哈希表是否滿了
????bool?isFull()?
????{?
????????//當(dāng)前的大小大于哈希表的大小
????????return?(curr_size?==?TABLE_SIZE);?
????}?
??
????//?哈希函數(shù)1
????int?hash1(int?key)?
????{?
????????return?(key?%?TABLE_SIZE);?
????}?
??
????//?哈希函數(shù)2
????int?hash2(int?key)?
????{?
????????return?(PRIME?-?(key?%?PRIME));?
????}?
???
????DoubleHash()?
????{?
????????hashTable?=?new?int[TABLE_SIZE];?
????????curr_size?=?0;?
????????for?(int?i?=?0;?i?????????????hashTable[i]?=?-1;???
????????}
????}?
??
????//?插入操作
????void?insertHash(int?key)?
????{?
????????//?判斷哈希表是否已滿
????????if?(isFull())?
????????????return;?
??
????????//?獲取哈希函數(shù)1計(jì)算的結(jié)果
????????int?index?=?hash1(key);?
??
????????//?如果發(fā)生碰撞?
????????if?(hashTable[index]?!=?-1)?{?
????????????//由哈希函數(shù)2獲取另一個(gè)哈希值
????????????int?index2?=?hash2(key);?
????????????int?i?=?1;?
????????????while?(1)?{?
????????????????//得到雙重哈希的索引,對(duì)于線性探測(cè),平方探測(cè)改這里就可以
????????????????int?newIndex?=?(index?+?i?*?index2)?%?TABLE_SIZE;?
??
????????????????//如果新的哈希值newIndex為空,退出循環(huán)。
????????????????if?(hashTable[newIndex]?==?-1)?{?
????????????????????hashTable[newIndex]?=?key;?
????????????????????break;?
????????????????}?
????????????????i++;?
????????????}?
????????}?
????????else{
????????????hashTable[index]?=?key;?
????????}
????????curr_size++;?
????}?
??
????//?哈希表查找操作
????void?search(int?key)?
????{?
????????int?index1?=?hash1(key);?
????????int?index2?=?hash2(key);?
????????int?i?=?0;?
????????while?(hashTable[(index1?+?i?*?index2)?%?TABLE_SIZE]?!=?key)?{?
????????????if?(hashTable[(index1?+?i?*?index2)?%?TABLE_SIZE]?==?-1)?{?
????????????????cout?<":\t哈希表中不存在"?<endl;?
????????????????//java?這里自己改成響應(yīng)輸出
????????????????return;?
????????????}?
????????????i++;?
????????}?
????????cout?<"找到啦!"?<endl;?
????}?
??
????//?打印輸出
????void?displayHash()?
????{?
????????for?(int?i?=?0;?i?????????????if?(hashTable[i]?!=?-1)?
????????????????cout?<"?-->?"
?????????????????????<endl;?
????????????else
????????????????cout?<endl;?
????????}?
????}?
};?
int?main()?
{?
????int?a[]?=?{50,?700,?76,?85,?92,?73,?101};?
????int?n?=?sizeof(a)?/?sizeof(a[0]);?
??
????//創(chuàng)建哈希表,插入a[]中的元素
????DoubleHash?h;?
????for?(int?i?=?0;?i?????????h.insertHash(a[i]);?
????}?
????//查找
????h.search(36);?//不存在
????h.search(101);?//存在
????//打印輸出
????h.displayHash();?
????return?0;?
}?
至于線性探測(cè)和平方探測(cè)的實(shí)現(xiàn)比較簡(jiǎn)單,只需要修改一下代碼中 newIndex 的計(jì)算方式即可。
線性探測(cè):
int?newIndex?=?(index?+?i)?%?TABLE_SIZE;?
平方探測(cè):
int?newIndex?=?(index?+?i*i)?%?TABLE_SIZE;?
以上三種探測(cè)方法的比較:
線性探測(cè)具有最佳的緩存性能,但會(huì)受到原始聚集(primary cluster)的影響。線性探測(cè)易于計(jì)算。
何為原始聚集(原始聚集是相對(duì)于線性探測(cè)而言的)?
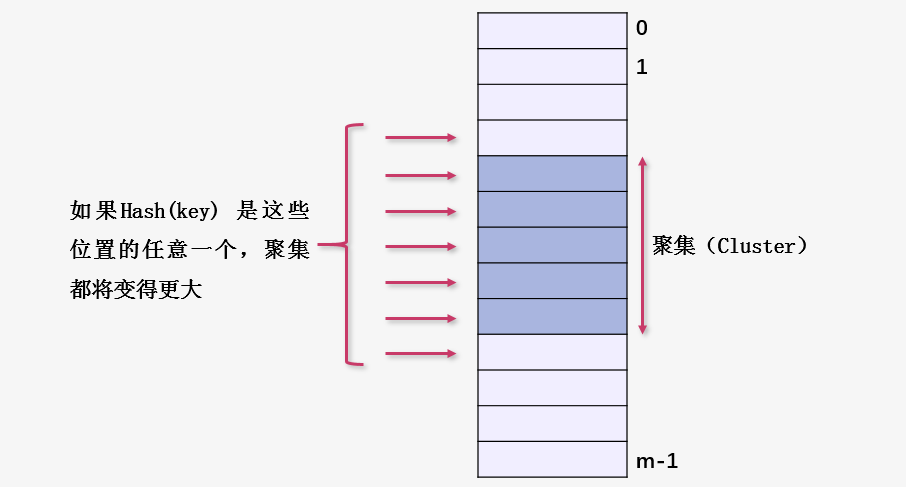
如圖所示,如果對(duì)于任意一個(gè)關(guān)鍵字 key ,其哈希值 Hash(key) 指向圖中從左向右的紅色箭頭的任意位置,聚集(圖中的淺藍(lán)色區(qū)域)都將得到擴(kuò)充,而隨著聚集的不斷擴(kuò)充,這個(gè)聚集會(huì)越來(lái)越大。
還不理解聚集的概念的話,我們一起看個(gè)例子:
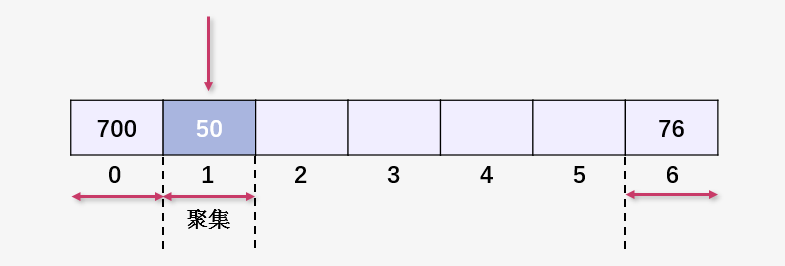
上圖中的 700,50,76 在插入的時(shí)候均未產(chǎn)生碰撞,所以以元素本身單位構(gòu)成聚集(聚集的大小為 1,此時(shí)可以認(rèn)為不是聚集)。
但是之后插入的元素就不一樣了,85 與 50 發(fā)生碰撞,插入到了 50 的后面,導(dǎo)致聚集變大。
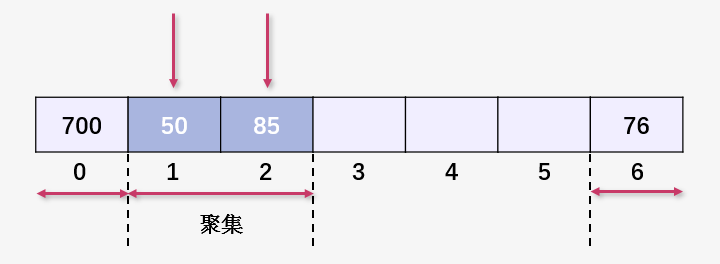
插入 92 與 50 發(fā)生碰撞,線性探測(cè)插入到了 85 之后,聚集進(jìn)一步擴(kuò)大。
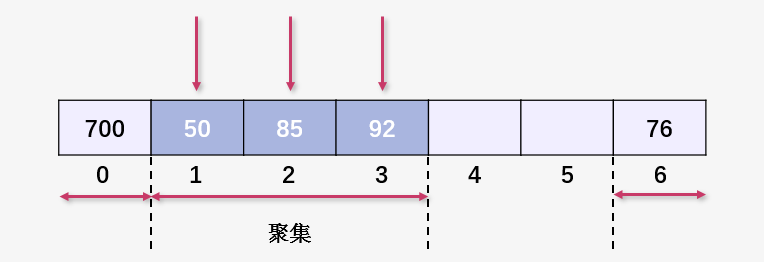
插入 73 與 92 產(chǎn)生碰撞,線性探測(cè)插入到 92 之后,聚集進(jìn)一步擴(kuò)大。
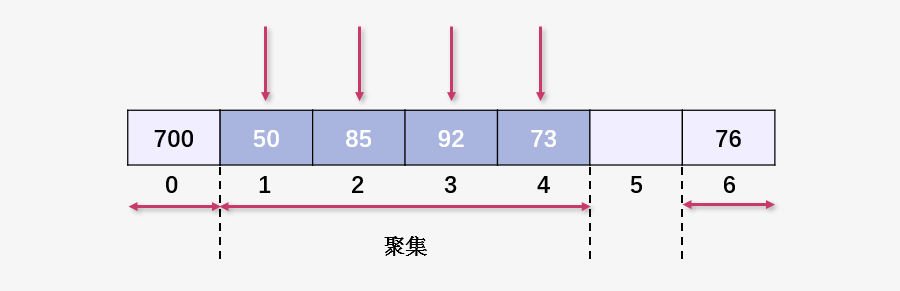
插入 101 與 92 產(chǎn)生碰撞,線性探測(cè)插入到 73 之后,聚集進(jìn)一步擴(kuò)大。

這就是原始聚集的概念,顯然聚集越大,產(chǎn)生碰撞的可能越來(lái)越大,哈希算法的性能也會(huì)受到影響。
平方探測(cè)在緩存性能和受聚集影響方面介于兩者中間,平方探測(cè)隨解決了線性探測(cè)的原始聚集問(wèn)題,但是同時(shí)也會(huì)產(chǎn)生更細(xì)的二次聚集問(wèn)題。
二重探測(cè)的緩存性能較差,但不用擔(dān)心聚集的情況,但同時(shí)由于要計(jì)算兩個(gè)散列函數(shù),時(shí)間性能方面受限。
開放地址法的性能分析
與鏈地址法類似,假設(shè)任何一個(gè)關(guān)鍵字都以相等的相等的概率被映射到哈希表的任意一個(gè)槽位。
其中 ?表示哈希表的槽位數(shù), 表示插入到哈希表中的關(guān)鍵字的數(shù)目。
裝填因子(load factor) (對(duì)于開放地址法而言, m > n)。
期望的插入、查找和刪除的時(shí)間 .
所以對(duì)于開放地址法而言,插入、查找和刪除的時(shí)間復(fù)雜度為 .
這里你一定會(huì)有困惑,舉個(gè)栗子, ,那么 則表示最多探測(cè)10次就可以查找、插入或刪除一個(gè)元素。
至于為什么是 ?
對(duì)這個(gè)感興趣的小伙伴,推薦看看嚴(yán)蔚敏老師的書籍《數(shù)據(jù)結(jié)構(gòu)(C語(yǔ)言版)》262 頁(yè)的證明。
開放地址法與鏈地址法的比較
所謂比較,算是對(duì)前面的一個(gè)總結(jié):
| No | 鏈地址法 | 開放地址法 |
|---|---|---|
| 1 | 易于實(shí)現(xiàn) | 需要更多的計(jì)算 |
| 2 | 使用鏈地址法,哈希表永遠(yuǎn)不會(huì)填充滿,不用擔(dān)心溢出。 | 哈希表可能被填滿,需要通過(guò)拷貝來(lái)動(dòng)態(tài)擴(kuò)容。 |
| 3 | 對(duì)于哈希函數(shù)和裝載因子不敏感 | 需要額外關(guān)注如何規(guī)避聚集以及裝載因子的選擇。 |
| 4 | 適合不知道插入和刪除的關(guān)鍵字的數(shù)量和頻率的情況 | 適合插入和刪除的關(guān)鍵字已知的情況。 |
| 5 | 由于使用鏈表來(lái)存儲(chǔ)關(guān)鍵字,緩存性能差。 | 所有關(guān)鍵字均存儲(chǔ)在同一個(gè)哈希表中,所以可以提供更好的緩存性能。 |
| 6 | 空間浪費(fèi)(哈希表中的有些鏈一直未被使用) | 哈希表中的所有槽位都會(huì)被充分利用。 |
| 7 | 指向下一個(gè)結(jié)點(diǎn)的指針要消耗額外的空間。 | 不存儲(chǔ)指針。 |
再哈希(Rehashing)
對(duì)于開放地址法而言,插入、查找和刪除的時(shí)間復(fù)雜度為 ,意味著哈希算法的時(shí)間復(fù)雜度取決于裝填因子 , ?越大,開放地址法的時(shí)間復(fù)雜度也就越高。
裝填因子 .
一般將裝填因子的值設(shè)置為 0.75,隨著填入哈希表中記錄數(shù)的增加,裝填因子就會(huì)增大甚至超過(guò)設(shè)置的默認(rèn)值 0.75,意味著哈希算法的時(shí)間復(fù)雜度的增加。為了解決裝填因子超過(guò)默認(rèn)設(shè)置的值 0.75,可以對(duì)數(shù)組(哈希表)進(jìn)行擴(kuò)容(二倍擴(kuò)容),并將原哈希表中的值進(jìn)行 再哈希,存儲(chǔ)到二倍大小的新數(shù)組(哈希表)中,從而保證裝填因子維持在一個(gè)較低的值(不超過(guò) 0.75),哈希算法的時(shí)間復(fù)雜度保證在 量級(jí)。
這就是為什么需要在哈希的原因所在,下面我們一起看一下再哈希的實(shí)現(xiàn)。
再哈希可以大致分為四個(gè)步驟:
對(duì)于每一次向哈希表中添加新的鍵值對(duì),檢查裝填因子 的大小; 如果 ,則進(jìn)行 再哈希 。 對(duì)于再哈希而言,創(chuàng)建一個(gè)新的數(shù)組(原數(shù)組的兩倍大小)作為哈希表。 遍歷原數(shù)組中的每一個(gè)元素,并將其插入到新的數(shù)組當(dāng)中。
我們依舊以 [50, 700, 76, 85, 92, 73, 101] 為例進(jìn)行說(shuō)明,其中可能會(huì)省略部分計(jì)算步驟。
開辟一個(gè)大小為 7 的空數(shù)組:
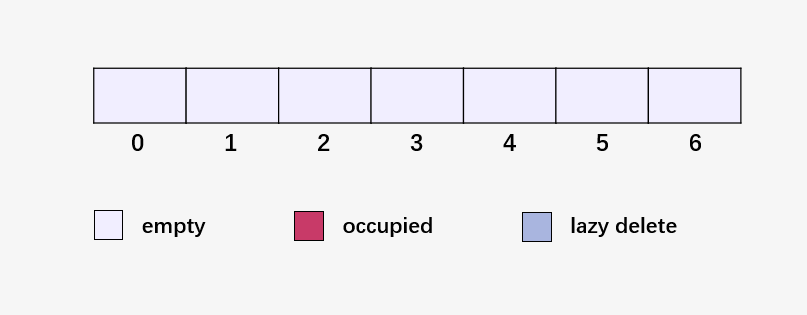
接下來(lái)就是插入并檢查裝填因子 ,我們將裝填因子自己寫到了圖中:
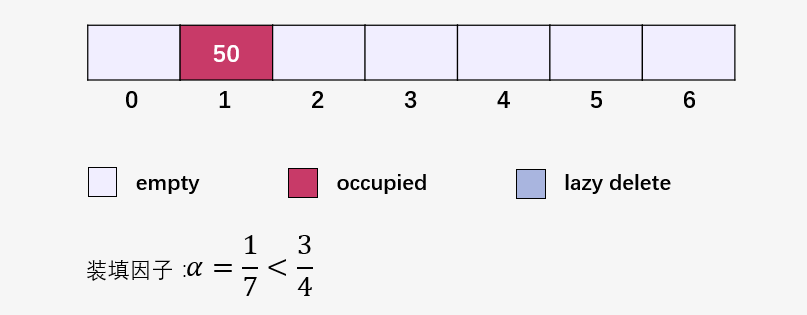
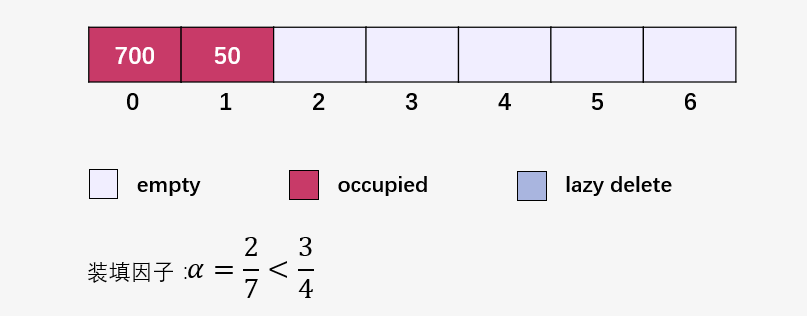
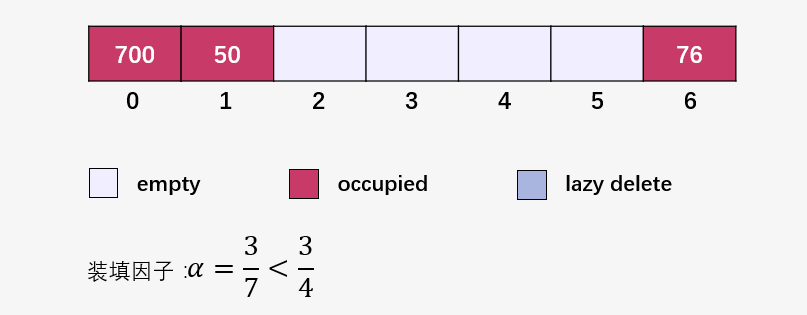
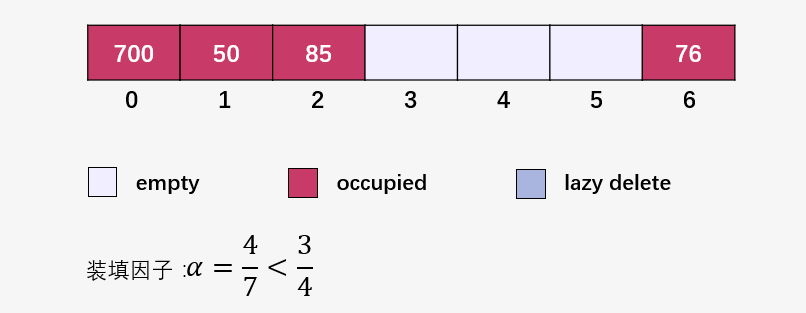
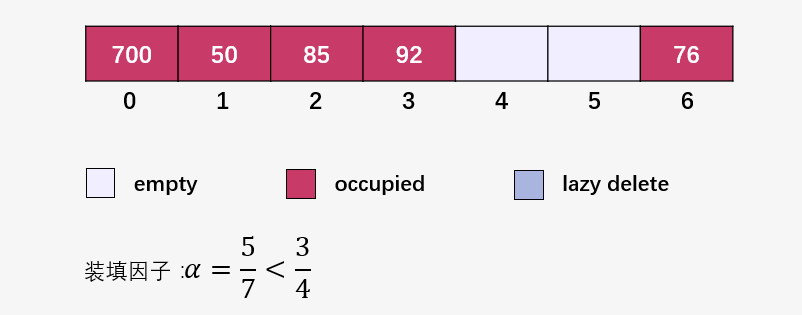
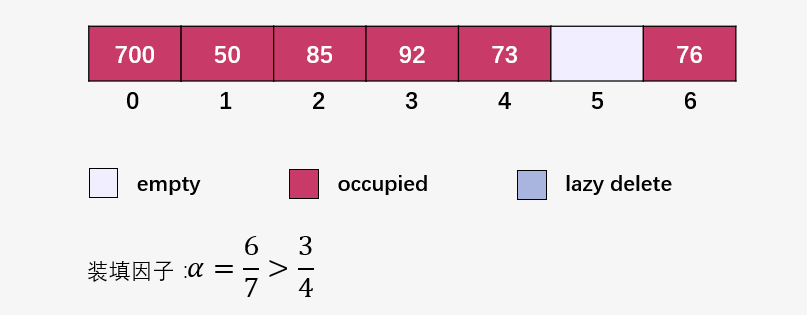
此時(shí)要注意啦,此時(shí)裝填因子 ,創(chuàng)建一個(gè)長(zhǎng)度為 14 的新數(shù)組(原始數(shù)組的兩倍):

此時(shí)的數(shù)組長(zhǎng)度為 14 ,我們的哈希函數(shù)也變了,由原來(lái)的 Hash(key) = key % 7 變成了 Hash(key) = key % 14 。然后遍歷原始數(shù)組,并將原始數(shù)組中的元素映射到新的數(shù)組當(dāng)中:
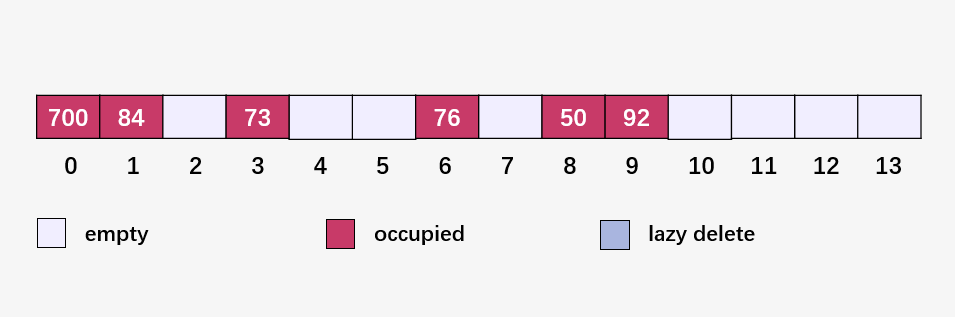
然后計(jì)算 101 % 14 = 3 ,插入到 73 的后面:
這就是再哈希,我相信你也理解啦!但是我們的實(shí)現(xiàn)可能不是這樣的,我們將插入的是一個(gè)鍵值對(duì),比如 [<50, "I">, <700, "Love">, <76, "Data">, <85, "Structure">, <92, "and">, <73, "Jing">, <101, "Yu">] 。此外代碼是以鏈地址法來(lái)實(shí)現(xiàn)再哈希的奧!可不是畫圖講的開放地址法線性探測(cè),如果不會(huì)寫開放地址法再哈希可以評(píng)論區(qū)留言,我寫了發(fā)你學(xué)習(xí)!
再哈希實(shí)現(xiàn)
import?java.util.ArrayList;?
??
class?Map<K,?V>?{?
??
????class?MapNode<K,?V>?{?
??
????????K?key;?
????????V?value;?
????????MapNode?next;?//鏈地址法
??
????????public?MapNode(K?key,?V?value)?
????????{?
????????????this.key?=?key;?
????????????this.value?=?value;?
????????????next?=?null;?
????????}?
????}?
??
????//?鍵值對(duì)就存儲(chǔ)在
????ArrayList?>?hashTable;?
??
????//?裝填因子?alpha?的分子?--?表中填入的記錄數(shù)
????int?size;?
??
????//?裝填因子 alpha 的分母?--?哈希表的長(zhǎng)度。
????int?numHashTable;?
??
????//?默認(rèn)的裝填因子?0.75?
????final?double?DEFAULT_LOAD_FACTOR?=?0.75;?
??
????public?Map()?
????{?
????????numHashTable?=?5;?
??
????????hashTable?=?new?ArrayList<>(numHashTable);?
??
????????for?(int?i?=?0;?i?????????????//?初始化哈希表?
????????????hashTable.add(null);?
????????}?
????}?
??
????private?int?getBucketInd(K?key)?
????{?
??
????????//?Using?the?inbuilt?function?from?the?object?class?
????????int?hashCode?=?key.hashCode();?
??
????????//?array?index?=?hashCode%numHashTable?
????????return?(hashCode?%?numHashTable);?
????}?
??
????public?void?insert(K?key,?V?value)?
????{?
????????//?獲取插入的關(guān)鍵字?key?的哈希值
????????int?bucketInd?=?getBucketInd(key);?
??
????????MapNode?head?=?hashTable.get(bucketInd);?
??
????????//插入?K-V
????????while?(head?!=?null)?{?
????????????if?(head.key.equals(key))?{?
????????????????head.value?=?value;?
????????????????return;?
????????????}?
????????????head?=?head.next;?
????????}?
???
????????MapNode?newElementNode?=?new?MapNode(key,?value);?
?
????????head?=?hashTable.get(bucketInd);?
????????newElementNode.next?=?head;?
??
????????hashTable.set(bucketInd,?newElementNode);?
?
????????size++;?
??
????????//?計(jì)算當(dāng)前的裝填因子?
????????double?loadFactor?=?(1.0?*?size)?/?numHashTable;?
??
????????//?裝填因子?>?0.75,執(zhí)行再哈希
????????if?(loadFactor?>?DEFAULT_LOAD_FACTOR)?{??
????????????rehash();?
????????}?
????}?
??
????private?void?rehash()?
????{?
??
????????System.out.println("\n***Rehashing?Started***\n");?
??
????????//?保存原始哈希表
????????ArrayList?>?temp?=?hashTable;?
??
????????//創(chuàng)建新的數(shù)組(原始數(shù)組的兩倍)
????????hashTable?=?new?ArrayList?>(2?*?numHashTable);?
??
????????for?(int?i?=?0;?i?2?*?numHashTable;?i++)?{??
????????????buckets.add(null);?
????????}?
????????//?將舊數(shù)組中數(shù)據(jù)拷貝到新數(shù)組中
????????size?=?0;?
????????numHashTable?*=?2;?
??
????????for?(int?i?=?0;?i?????????????MapNode?head?=?temp.get(i);?
??
????????????while?(head?!=?null)?{?
????????????????K?key?=?head.key;?
????????????????V?val?=?head.value;?
?
????????????????insert(key,?val);?
????????????????head?=?head.next;?
????????????}?
????????}??
????}?
??
????public?void?printMap()?
????{?
????????ArrayList?>?temp?=?hashTable;?
??
????????System.out.println("當(dāng)前的哈希表:");?
????????for?(int?i?=?0;?i?????????????//?獲取哈希表當(dāng)前?i?的頭結(jié)點(diǎn)
????????????MapNode?head?=?temp.get(i);?
??
????????????while?(head?!=?null)?{?
????????????????System.out.println("key?=?"?+?head.key?+?",?
???????????????????????????????????val?=?"?+?head.value);?
??
????????????????head?=?head.next;?
????????????}?
????????}?
????????System.out.println();?
????}?
}?
??
public?class?Rehashing?{?
??
????public?static?void?main(String[]?args)?
????{?
??
????????//?創(chuàng)建一個(gè)哈希表?
????????Map?map?=?new?Map();?
??
????????//?插入元素[<50,?"I">,?<700,?"Love">,?<76,?"Data">,?
????????//<85,?"Structure">,?<92,?"and">,?<73,?"Jing">,?<101,?"Yu">]
????????map.insert(50,?"I");?
????????map.printMap();?
??
????????map.insert(700,?"Love");?
????????map.printMap();?
??
????????map.insert(76,?"Data");?
????????map.printMap();?
??
????????map.insert(85,?"Structure");?
????????map.printMap();?
??
????????map.insert(92,?"and");?
????????map.printMap();?
????????map.insert(73,?"Jing");?
????????map.printMap();?
????????map.insert(101,?"Yu");?
????????map.printMap();?
????}?
}?
哈希算法的應(yīng)用
哈希算法在日常生活中的應(yīng)用非常普遍,包括信息摘要(Message Digest),密碼校驗(yàn)(Password Verification),數(shù)據(jù)結(jié)構(gòu)(編程語(yǔ)言),編譯操作(Compiler Operation),Rabin-Karp 算法(模式匹配算法),負(fù)載均衡等等。
當(dāng)你注冊(cè)一個(gè)網(wǎng)站在客戶端輸入郵箱和密碼時(shí),客戶端會(huì)對(duì)用戶輸入的密碼進(jìn)行 hash 運(yùn)算,然后在服務(wù)端的數(shù)據(jù)庫(kù)中保存用戶密碼的 Hash 值,從而保護(hù)用戶的數(shù)據(jù)。
C++ 當(dāng)中的 unordered_set & unordered_map ,以及 Java 中 HashSet & HashMap 和 Python 中的 dict 等各種編程語(yǔ)言均實(shí)現(xiàn)了哈希表數(shù)據(jù)結(jié)構(gòu)。
Rabin-Karp 算法利用哈希來(lái)查找字符串的任意一組模式,并且可以用來(lái)檢查抄襲。
可以利用一致性哈希解決負(fù)載均衡問(wèn)題。
同樣可以用于版本校驗(yàn)、防篡改、密碼校驗(yàn),此外還廣泛應(yīng)用于各類數(shù)據(jù)庫(kù)當(dāng)中(包括MySQL、Redis等等)。
關(guān)于哈希算法應(yīng)用的詳細(xì)內(nèi)容大家可以看看參考資料[1]。
參考資料
[1] https://www.zhihu.com/question/26762707/answer/890181997
[2] https://hit-alibaba.github.io/interview/basic/algo/Hash-Table.html
[3] 嚴(yán)蔚敏老師的《數(shù)據(jù)結(jié)構(gòu)(C語(yǔ)言)》版。
[4] https://www.cs.princeton.edu/~rs/AlgsDS07/10Hashing.pdf
[5] http://courses.csail.mit.edu/6.006/fall09/lecture_notes/lecture05.pdf
[6] http://courses.csail.mit.edu/6.006/fall11/lectures/lecture10.pdf
[7] https://www.cse.cuhk.edu.hk/irwin.king/_media/teaching/csc2100b/tu6.pdf
來(lái)個(gè)直擊靈魂的三連吧!
