如何看待李沐老師提出的「用隨機梯度下降來優(yōu)化人生」?
來源:知乎
電光幻影煉金術(上海交大計算機第一名)回答:
看完李沐老師的文章,深受啟發(fā)。本人閱讀大量文獻,提出了下面“反向利用隨機梯度下降優(yōu)化人生“的方案。下文與李沐老師的文章的原文(在引用塊里)一一對應進行回答。
李沐:目標要大。不管是人生目標還是目標函數(shù),你最好不要知道最后可以走到哪里。如果你知道,那么你的目標就太簡單了,可能是個凸函數(shù)。你可以在一開始的時候給自己一些小目標,例如期末考個80分,訓練一個線性模型。但接下來得有更大的目標,財富自由也好,100億參數(shù)的變形金剛也好,得足夠一顆賽艇。
反向:目標要小而具體。如果目標過大,很容易導致因為噪聲過大,獎勵過于稀疏而發(fā)散[1]。收斂情況很好的,往往是圖片分類這種目標非常明確而具體的任務。與之相反,在真實機器人面臨的搜索空間很大的場景,隨機梯度下降很容易發(fā)散[2]。
李沐:堅持走。不管你的目標多復雜,隨機梯度下降都是最簡單的。每一次你找一個大概還行的方向(梯度),然后邁一步(下降)。兩個核心要素是方向和步子的長短。但最重要的是你得一直走下去,能多走幾步就多走幾步。
反向:該放棄時就要放棄。一個簡單也很有效的解決梯度策略發(fā)散的技巧就是拋棄過大的梯度[3]。如果遇到很大的梯度還不選擇拋棄或者裁剪,很容易會導致發(fā)散的結果。除此之外,很多場合使用隨機梯度下降訓練幾個epoch會發(fā)現(xiàn)梯度越來越大,這時候一定要及時停下來檢查數(shù)據(jù)。不然一晚上過后只能得到一個NAN(發(fā)散)的結果,白白浪費寶貴的算力資源。
李沐:痛苦的卷。每一步里你都在試圖改變你自己或者你的模型參數(shù)。改變帶來痛苦。但沒有改變就沒有進步。你過得很痛苦不代表在朝著目標走,因為你可能走反了。但過得很舒服那一定在原地踏步。需要時刻跟自己作對。
反向:拒絕內(nèi)卷。優(yōu)化有兩種模式,一種很陡峭曲折的(比較艱難,對應內(nèi)卷),一種是比較平滑的(比較輕松,對應佛系和不卷)。這里我引用一篇頂會論文中[4]的可視化結果,

上圖左邊的(a)優(yōu)化曲面不平滑,對應很內(nèi)卷的殘酷場景;右邊的(b)是很平滑的過程,對應不內(nèi)卷的自由發(fā)展。那么究竟是(a)好呢,還是(b)好呢?想必大家已經(jīng)猜到了,(b)這種優(yōu)化模式要遠遠好于(a),錯誤率小兩倍多(錯誤率:(b)5.89%,(a)13.31%)。因此,大家一定要學會拒絕內(nèi)卷,保護自己平滑的成長過程。
李沐: 四處看看。每一步走的方向是你對世界的認識。如果你探索的世界不怎么變化,那么要么你的目標太簡單,要么你困在你的舒適區(qū)了。隨機梯度下降的第一個詞是隨機,就是你需要四處走走,看過很多地方,做些錯誤的決定,這樣你可以在前期邁過一些不是很好的舒適區(qū)。
反向:別走太遠。正則化是深度學習乃至機器學習中非常常見的技巧,要想取得好的收斂效果,往往需要加以約束,不能走得太遠[3]。放任自我也會容易導致發(fā)散。
李沐: 贏在起點。起點當然重要。如果你在終點附近起步,可以少走很多路。而且終點附近的路都比較平,走著舒服。當你發(fā)現(xiàn)別人不如你的時候,看看自己站在哪里。可能你就是運氣很好,贏在了起跑線。如果你跟別人在同一起跑線,不見得你能做更好。
反向:起點不重要。Facebook公司Kaiming大神的一篇論文[5]用大量實驗事實證明,接受預訓練的模型,雖然一開始會好一些,但是后面跟隨機初始化的模型相差無幾。有實驗結果圖為證:
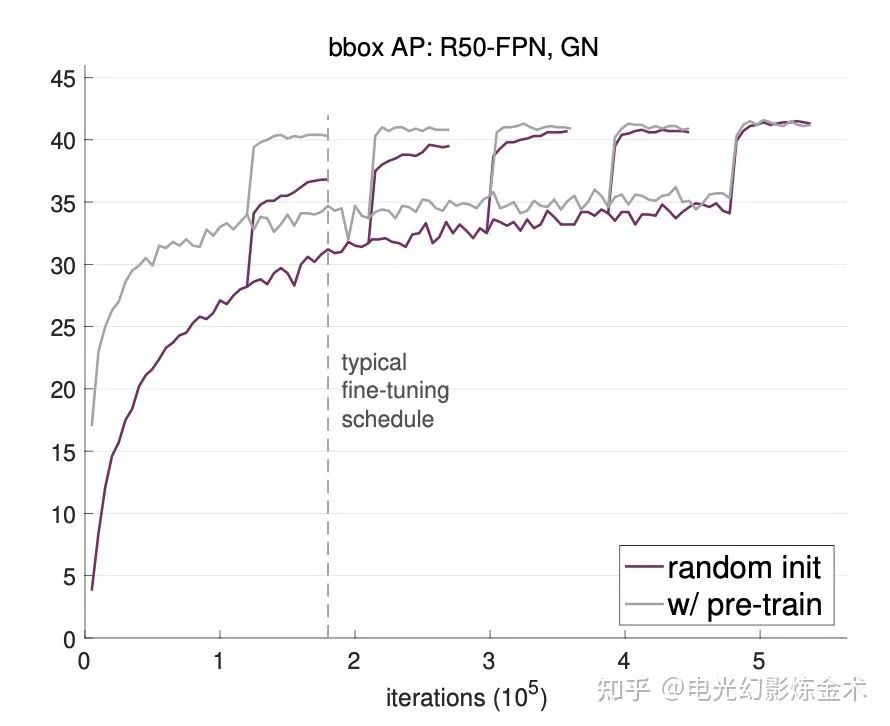
李沐: 很遠也能到達。如果你是在隨機起點,那么做好準備前面的路會非常不平坦。越遠離終點,越人跡罕見。四處都是懸崖。但隨機梯度下降告訴我們,不管起點在哪里,最后得到的解都差不多。當然這個前提是你得一直按照梯度的方向走下去。如果中間梯度炸掉了,那么你隨機一個起點,調(diào)整步子節(jié)奏,重新來。
反向:太遠就到不了了。如果間隔時間太長,獎勵函數(shù)的折損會非常嚴重,導致強化學習的成功率不高。這也是強化學習目前只能在模擬器中成功(無法在真實的機器人上被廣泛應用)的主要原因之一。

李沐:簡單最好。當然有比隨機梯度下降更復雜的算法。他們想每一步看想更遠更準,想步子邁最大。但如果你的目標很復雜,簡單的隨機梯度下降反而效果最好。深度學習里大家都用它。關注當前,每次抬頭瞄一眼世界,快速做個決定,然后邁一小步。小步快跑。只要你有目標,不要停,就能到達。
反向:越結構化的模型越好。文獻顯示[6],拓撲結構較復雜的模型,在同樣的梯度下降算法之后會產(chǎn)生更小的泛化誤差。而過于簡單的模型,往往會容易收斂到平凡解,喪失足夠的泛化能力。

不是很懂優(yōu)化這塊,歡迎批評指點。
有些點沒講到,是因為找不到特別好的文獻,或者讀起來沒那么有趣。
如果要我說,人生反正不是監(jiān)督學習,更像是強化學習甚至無監(jiān)督學習。
當然,也可能人生就是隨機挑戰(zhàn)。
Towser回答:
然而,除了優(yōu)化算法還有初始化:有些人有預訓練模型,一出生就在最優(yōu)點附近,隨便走兩步就比大多數(shù)人吭哧吭哧走半天效果還好;有些人出生在懸崖邊上,一步走錯就萬劫不復。
然而,除了優(yōu)化算法還有損失函數(shù):有些人的損失函數(shù)是強凸的,優(yōu)化的方向非常明確,或者是有很強的正則項,走錯的時候可以把他往回拉;有些人的損失函數(shù)數(shù)值極其不穩(wěn)定,動不動就爆 NaN/Inf。
就算是優(yōu)化算法,也要看你能拿到什么信息:有些人是一階優(yōu)化,跟著梯度信息慢慢往前走;有些人是零階優(yōu)化,拿不到梯度信息,就只能自己摸黑瞎走走。
參考
^Hare, Joshua. "Dealing with sparse rewards in reinforcement learning." arXiv preprint arXiv:1910.09281 (2019).
^Peters, Jan, and Stefan Schaal. "Policy gradient methods for robotics." 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE, 2006.
^abSchulman, John, et al. "Proximal policy optimization algorithms." arXiv preprint arXiv:1707.06347 (2017).
^Li, Hao, et al. "Visualizing the loss landscape of neural nets." arXiv preprint arXiv:1712.09913 (2017).
^He, Kaiming, Ross Girshick, and Piotr Dollár. "Rethinking imagenet pre-training." Proceedings of the IEEE/CVF International Conference on Computer Vision. 2019.
^Corneanu, Ciprian A., Sergio Escalera, and Aleix M. Martinez. "Computing the testing error without a testing set." Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. 2020.
——The End——
為了方便大家學習,我們建立微信交流群,歡迎大家加我的微信,邀你進群!
微商無關人員勿擾!



