Python時間序列分析全面指南(附代碼)
作者：Selva Prabhakaran? ? ? ? ???
翻譯：陳超? ? ? ? ? ?校對：王可汗
本文約7500字，建議閱讀20+分鐘
本文介紹了時間序列的定義、特征并結合實例給出了時間序列在Python中評價指標和方法。
內容
1. 什么是時間序列？
2. 如何在Python中導入時間序列？
3. 什么是面板數(shù)據(jù)？
4.?時間序列可視化
5.?時間序列的模式
6.?時間序列的加法和乘法
7. 如何將時間序列分解？
8.?平穩(wěn)和非平穩(wěn)時間序列
9. 如何獲取平穩(wěn)的時間序列？
10. 如何檢驗平穩(wěn)性？
11. 白噪音和平穩(wěn)序列的差異是什么？
12. 如何去除時間序列的線性分量？
13. 如何消除時間序列的季節(jié)性？
14. 如何檢驗時間序列的季節(jié)性？
15. 如何處理時間序列中的缺失值？
16. 什么是自回歸和偏自回歸函數(shù)？
17. 如何計算偏自回歸函數(shù)？
18.?滯后圖
19. 如何估計時間序列的預測能力？
20. 為什么以及怎樣使時間序列平滑？
21. 如何使用Granger因果檢驗來獲知時間序列是否對預測另一個序列幫助？
22.?下一步是什么?
? 1. 什么是時間序列?時間序列是在規(guī)律性時間間隔記錄的觀測值序列。
依賴于觀測值的頻率，典型的時間序列可分為每小時、每天、每周、每月、每季度和每年為單位記錄。有時，你可能也會用到以秒或者分鐘為單位的時間序列，比如，每分鐘用戶點擊量和訪問量等等。
1.1 為什么要分析時間序列呢？
因為它是你做序列預測前的一步準備過程。而且，時間序列預測擁有巨大的商業(yè)重要性，因為對商業(yè)來說非常重要的需求和銷量、網站訪問人數(shù)、股價等都是時間序列數(shù)據(jù)。
1.2 所以時間序列分析包括什么內容呢？
時間序列分析包括理解序列內在本質的多個方面以便于你可更好地了解如何做出有意義并且精確的預測。
2. 如何在Python中導入時間序列？
讓我們用pandas包里的read.csv()讀取時間序列數(shù)據(jù)（一個澳大利亞藥品銷售的csv文件）作為一個pandas數(shù)據(jù)框。加入parse_dates=[‘date’]參數(shù)將會把日期列解析為日期字段。
from dateutil.parser import parse
import matplotlib as mpl
import matplotlib.pyplot as plt
import seaborn as sns
import numpy as np
import pandas as pd
plt.rcParams.update({'figure.figsize': (10, 7), 'figure.dpi': 120})
# Import as Dataframe
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])
df.head()
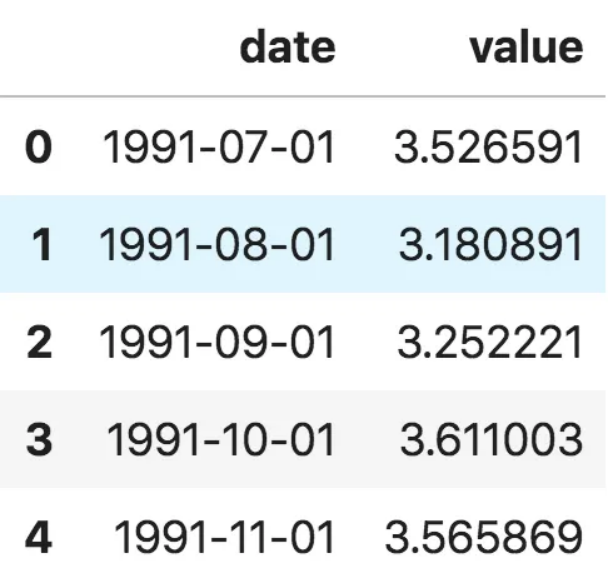
此外，你也可以將其導入為date作為索引的pandas序列。你只需要固定pd.read_csv()里的index_col參數(shù)。
ser = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
ser.head()
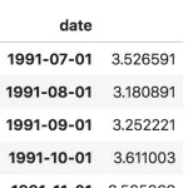
注意，在此序列當中，‘value’列的位置高于date以表明它是一個序列。
3. 什么是面板數(shù)據(jù)？
面板數(shù)據(jù)也是基于時間的數(shù)據(jù)集。
差異在于，除了時間序列，它也包括同時測量的一個或多個相關變量。
通常來看，面板數(shù)據(jù)當中的列包括了有助于預測Y的解釋型變量，假設這些列將在未來預測階段有用。
面板數(shù)據(jù)的例子如下：
# dataset source: https://github.com/rouseguy
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/MarketArrivals.csv')
df = df.loc[df.market=='MUMBAI', :]
df.head()
?
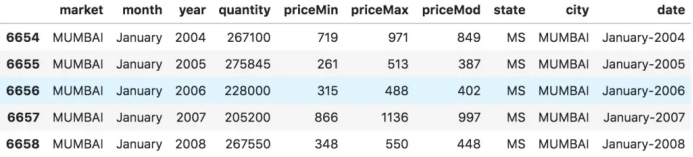
4. 時間序列可視化
# Time series data source: fpp pacakge in R.
import matplotlib.pyplot as plt
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
# Draw Plot
def plot_df(df, x, y, title="", xlabel='Date', ylabel='Value', dpi=100):
plt.figure(figsize=(16,5), dpi=dpi)
plt.plot(x, y, color='tab:red')
plt.gca().set(title=title, xlabel=xlabel, ylabel=ylabel)
plt.show()
plot_df(df, x=df.index, y=df.value, title='Monthly anti-diabetic drug sales in Australia from 1992 to 2008.')
?
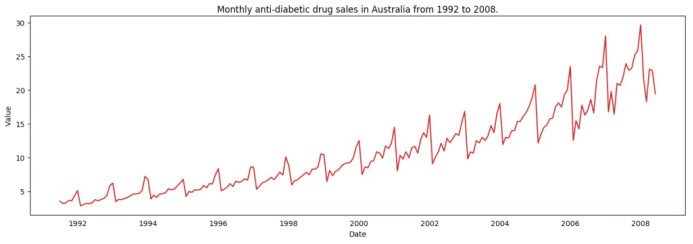?時間序列可視化
# Import data
df = pd.read_csv('datasets/AirPassengers.csv', parse_dates=['date'])
x = df['date'].values
y1 = df['value'].values
# Plot
fig, ax = plt.subplots(1, 1, figsize=(16,5), dpi= 120)
plt.fill_between(x, y1=y1, y2=-y1, alpha=0.5, linewidth=2, color='seagreen')
plt.ylim(-800, 800)
plt.title('Air Passengers (Two Side View)', fontsize=16)
plt.hlines(y=0, xmin=np.min(df.date), xmax=np.max(df.date), linewidth=.5)
plt.show()
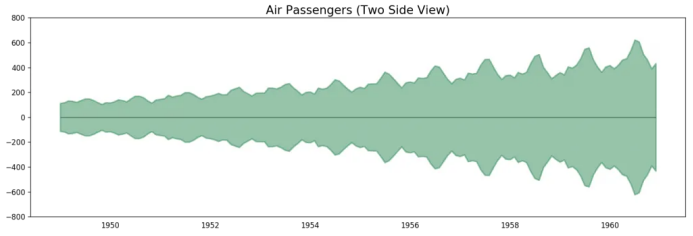
因為這是一個月度時間序列，每年遵循特定的重復模式，你可以把每年作為一個單獨的線畫在同一張圖上。這可以讓你同時比較不同年份的模式。
4.1 時間序列的季節(jié)圖
# Import Data
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
df.reset_index(inplace=True)
# Prepare data
df['year'] = [d.year for d in df.date]
df['month'] = [d.strftime('%b') for d in df.date]
years = df['year'].unique()
# Prep Colors
np.random.seed(100)
mycolors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)
# Draw Plot
plt.figure(figsize=(16,12), dpi= 80)
for i, y in enumerate(years):
if i > 0:
plt.plot('month', 'value', data=df.loc[df.year==y, :], color=mycolors[i], label=y)
plt.text(df.loc[df.year==y, :].shape[0]-.9, df.loc[df.year==y, 'value'][-1:].values[0], y, fontsize=12, color=mycolors[i])
# Decoration
plt.gca().set(xlim=(-0.3, 11), ylim=(2, 30), ylabel='$Drug Sales$', xlabel='$Month$')
plt.yticks(fontsize=12, alpha=.7)
plt.title("Seasonal Plot of Drug Sales Time Series", fontsize=20)
plt.show()
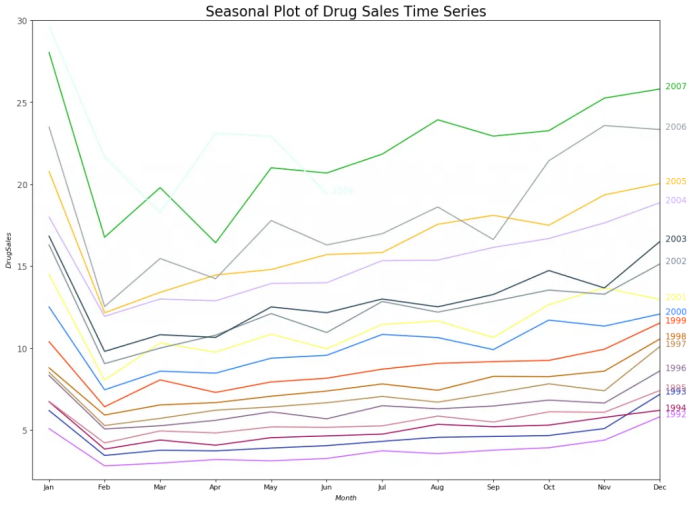
每年二月會迎來藥品銷售的急速下降，而在三月會再度上升，接下來的4月又開始下降，以此類推。很明顯，該模式在特定的某一年中重復，且年年如此。
然而，隨著年份推移，藥品銷售整體增加。你可以很好地看到該趨勢并且在年份箱線圖當中看到它是怎樣變化的。同樣地，你也可以做一個月份箱線圖來可視化月度分布情況。
4.2 月度（季節(jié)性）箱線圖和年度（趨勢）分布
你可以季節(jié)間隔將數(shù)據(jù)分組，并看看在給定的年份或月份當中值是如何分布的，以及隨時間推移它們是如何比較的。
# Import Data
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
df.reset_index(inplace=True)
# Prepare data
df['year'] = [d.year for d in df.date]
df['month'] = [d.strftime('%b') for d in df.date]
years = df['year'].unique()
# Draw Plot
fig, axes = plt.subplots(1, 2, figsize=(20,7), dpi= 80)
sns.boxplot(x='year', y='value', data=df, ax=axes[0])
sns.boxplot(x='month', y='value', data=df.loc[~df.year.isin([1991, 2008]), :])
# Set Title
axes[0].set_title('Year-wise Box Plot\n(The Trend)', fontsize=18);
axes[1].set_title('Month-wise Box Plot\n(The Seasonality)', fontsize=18)
plt.show()
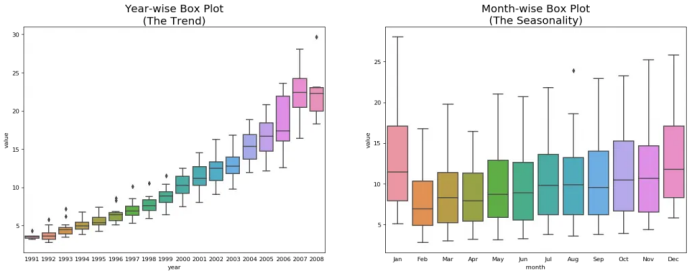
箱線圖將年度和月度分布變得很清晰。并且，在閱讀箱線圖當中，12月和1月明顯有更高的藥品銷售量，可被歸因于假期折扣季。
到目前為止，我們已經看到了識別模式的相似之處。現(xiàn)在怎樣才能從通常模式當中找到離群值呢？
5. 時間序列的模式
當在時間序列當中觀測到增加或降低的斜率時，即可觀測到相應的趨勢。然而季節(jié)性只有在由于季節(jié)性因素導致不同的重復模式在規(guī)律性的間隔之間被觀測到時才能發(fā)現(xiàn)。可能是由于當年的特定月份，特定月份的某一天、工作日或者甚至是當天某個時間。
然而，并不是所有時間序列必須有一個趨勢和/或季節(jié)性。時間序列可能沒有不同的趨勢但是有一個季節(jié)性。反之亦然。
所以時間序列可以被看做是趨勢、季節(jié)性和誤差項的整合。
fig, axes = plt.subplots(1,3, figsize=(20,4), dpi=100)
pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/guinearice.csv', parse_dates=['date'], index_col='date').plot(title='Trend Only', legend=False, ax=axes[0])
pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv', parse_dates=['date'], index_col='date').plot(title='Seasonality Only', legend=False, ax=axes[1])
pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/AirPassengers.csv', parse_dates=['date'], index_col='date').plot(title='Trend and Seasonality', legend=False, ax=axes[2])
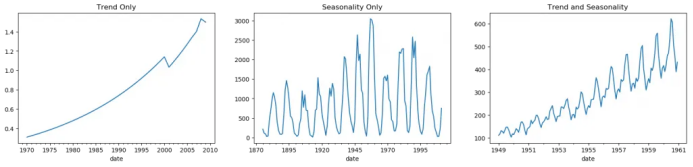
另一個需要考慮的方面是循環(huán)的行為。當序列當中上升和下降模式并不在固定的日歷間隔出現(xiàn)時，就會出現(xiàn)循環(huán)的行為。需注意不要混淆循環(huán)的效應和季節(jié)的效應。
所以，怎樣區(qū)分循環(huán)的和季節(jié)性的模式呢？
如果模式不是基于固定的日歷頻率，那它就是循環(huán)的。因為，循環(huán)效應不像季節(jié)性那樣受到商業(yè)和其他社會經濟因素的影響。
6. 時間序列的加法和乘法
加法時間序列： 值=基線水平+趨勢+季節(jié)性+誤差
乘法時間序列： 值=基線水平*趨勢*季節(jié)性*誤差
7. 怎樣分解時間序列的成分？
statsmodels包里的seasonal_decompose使用起來非常方便。
from statsmodels.tsa.seasonal import seasonal_decompose
from dateutil.parser import parse
# Import Data
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
# Multiplicative Decomposition
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
# Additive Decomposition
result_add = seasonal_decompose(df['value'], model='additive', extrapolate_trend='freq')
# Plot
plt.rcParams.update({'figure.figsize': (10,10)})
result_mul.plot().suptitle('Multiplicative Decompose', fontsize=22)
result_add.plot().suptitle('Additive Decompose', fontsize=22)
plt.show()
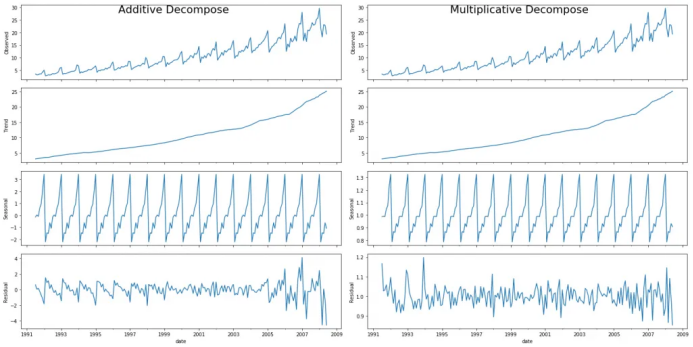
在序列開始時，設置extrapolate_trend='freq'?來注意趨勢和殘差中缺失的任何值。
如果你仔細看加法分解當中的殘差，它有一些遺留模式。乘法分解看起來非常隨意，這很好。所以理想狀況下，乘法分解應該在這種特定的序列當中優(yōu)先選擇。
趨勢，季節(jié)性和殘差成分的數(shù)值輸出被存儲在result_mul 當中。讓我們提取它們并導入數(shù)據(jù)框中。
# Extract the Components ----
# Actual Values = Product of (Seasonal * Trend * Resid)
df_reconstructed = pd.concat([result_mul.seasonal, result_mul.trend, result_mul.resid, result_mul.observed], axis=1)
df_reconstructed.columns = ['seas', 'trend', 'resid', 'actual_values']
df_reconstructed.head()
如果你檢查一下seas, trend 和 resid列的乘積，應該確實等于actual_values。
8. 平穩(wěn)和非平穩(wěn)時間序列
也就是說，這種序列的統(tǒng)計屬性例如均值，方差和自相關是隨時間不變的常數(shù)。序列的自相關只是與前置值的相關，之后會詳細介紹。
平穩(wěn)時間序列也沒有季節(jié)效應。
所以如何識別一個序列是否平穩(wěn)呢？讓我們通過實例來展示一下：
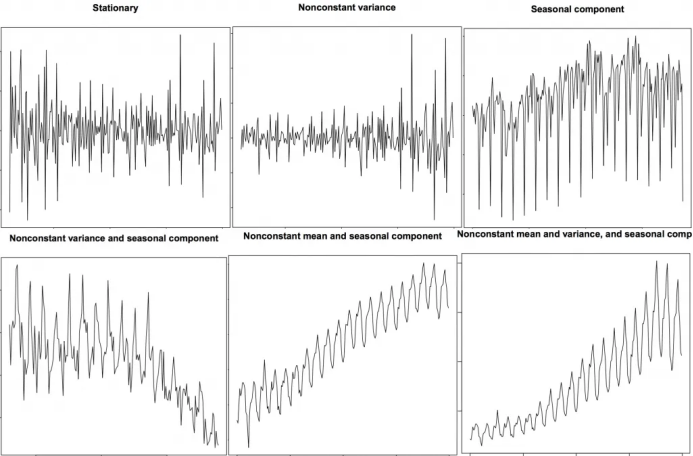
上圖來自R語言的 TSTutorial。
所以為什么平穩(wěn)序列是重要的呢？為什么我要提到它？
我將展開講一下，但是要理解它只是有可能通過使用特定的轉換方法實現(xiàn)任何時間序列的平穩(wěn)化。大多數(shù)統(tǒng)計預測方法都用于平穩(wěn)時間序列。預測的第一步通常是做一些轉換將非平穩(wěn)數(shù)據(jù)轉化為平穩(wěn)數(shù)據(jù)。
9. 如何獲取平穩(wěn)的時間序列？
1. 差分序列（一次或多次）； 2. 對序列值進行l(wèi)og轉換； 3. 對序列值去n次根式值； 4. 結合上述方法。
實現(xiàn)數(shù)據(jù)平穩(wěn)化最常見也最方便的方法是對序列進行差分至少一次，直到它變得差不多平穩(wěn)為止。
9.1 所以什么是差分？
如果Y_t是t時刻的Y值，那么第一次差分Y = Yt – Yt-1。在簡化的格式當中，差分序列就是從當前值中減去下一個值。
如果第一次差分不能使數(shù)據(jù)平穩(wěn)，你可以第二次差分，以此類推。
例如，考慮如下序列: [1, 5, 2, 12, 20]
一次差分: [5-1, 2-5, 12-2, 20-12] = [4, -3, 10, 8] 二次差分: [-3-4, -10-3, 8-10] = [-7, -13, -2]
9.2? 為什么要在預測之前將非平穩(wěn)數(shù)據(jù)平穩(wěn)化？
一個重要的原因是自回歸預測模型必須是利用序列自身的滯后量作為預測變量的線性回歸模型。
我們知道線性回歸在預測變量（X變量）與其他變量不相關時效果最佳。所以序列平穩(wěn)化也因為移除所有持續(xù)的自相關而解決了這個問題，因此使得模型中的預測變量（序列的滯后值）幾乎獨立。
現(xiàn)在我們已經建立了序列平穩(wěn)化非常重要的概念，那怎樣檢驗給定序列是否平穩(wěn)化呢？
10. 怎樣檢驗平穩(wěn)性?
另外一種方法是將序列分成2或多個連續(xù)的部分，計算概要統(tǒng)計量例如均值，方差和自相關。如果統(tǒng)計量顯著差異，序列可能不是平穩(wěn)的。
盡管如此，你需要一個方法來從量化的角度判斷一個給定序列是否平穩(wěn)。可以通過‘Unit Root Tests單位根檢驗’來實現(xiàn)。這里有多種變式，但這些檢驗都是用來檢測時間序列是否非平穩(wěn)并且擁有一個單位根。
有多種單位根檢驗的具體應用：
1.?增廣迪基·富勒檢驗（ADF Test）； 2. 科維亞特夫斯基-菲利普斯-施密特-辛-KPSS檢驗（趨勢平穩(wěn)性）； 3. 菲利普斯 佩龍檢驗（PP Test）。
最常用的是ADF檢驗，零假設是時間序列只有一個單位根并且非平穩(wěn)。所以ADF檢驗p值小于0.05的顯著性水平，你拒絕零假設。
KPSS檢驗，另一方面，用于檢驗趨勢平穩(wěn)性。零假設和p值解釋與ADH檢驗相反。下面的代碼使用了python中的statsmodels包來做這兩種檢驗。
from statsmodels.tsa.stattools import adfuller, kpss
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])
# ADF Test
result = adfuller(df.value.values, autolag='AIC')
print(f'ADF Statistic: {result[0]}')
print(f'p-value: {result[1]}')
for key, value in result[4].items():
print('Critial Values:')
print(f' {key}, {value}')
# KPSS Test
result = kpss(df.value.values, regression='c')
print('\nKPSS Statistic: %f' % result[0])
print('p-value: %f' % result[1])
for key, value in result[3].items():
print('Critial Values:')
print(f' {key}, {value}')
ADF Statistic: 3.14518568930674
p-value: 1.0
Critial Values:
1%, -3.465620397124192
Critial Values:
5%, -2.8770397560752436
Critial Values:
10%, -2.5750324547306476
KPSS Statistic: 1.313675
p-value: 0.010000
Critial Values:
10%, 0.347
Critial Values:
5%, 0.463
Critial Values:
2.5%, 0.574
Critial Values:
1%, 0.739
11. 白噪音和平穩(wěn)序列的差異是什么？
無論怎樣，在白噪音當中是沒有特定模式的。如果你將FM廣播的聲音信號作為時間序列，你在頻道之間的頻段聽到的空白聲就是白噪音。
從數(shù)學上來看，均值為0的完全隨機的數(shù)字序列是白噪音。
randvals = np.random.randn(1000)
pd.Series(randvals).plot(title='Random White Noise', color='k')
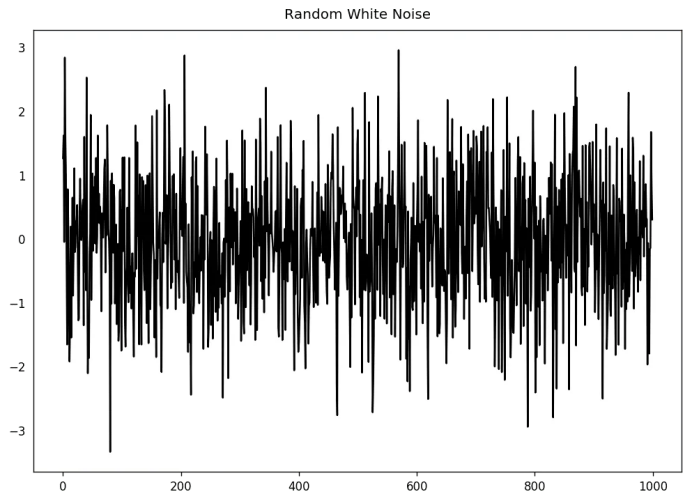
12. 怎樣將時間序列去趨勢化？
1. 從時間序列當中減去最優(yōu)擬合線。最佳擬合線可從以時間步長為預測變量獲得的線性回歸模型當中獲得。對更復雜的模型，你可以使用模型中的二次項（x^2）； 2. 從我們之前提過的時間序列分解當中減掉趨勢成分； 3. 減去均值； 4. 應用像Baxter-King過濾器(statsmodels.tsa.filters.bkfilter)或者Hodrick-Prescott 過濾器?(statsmodels.tsa.filters.hpfilter)來去除移動的平均趨勢線或者循環(huán)成分。
讓我們來用一下前兩種方法。
# Using scipy: Subtract the line of best fit
from scipy import signal
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])
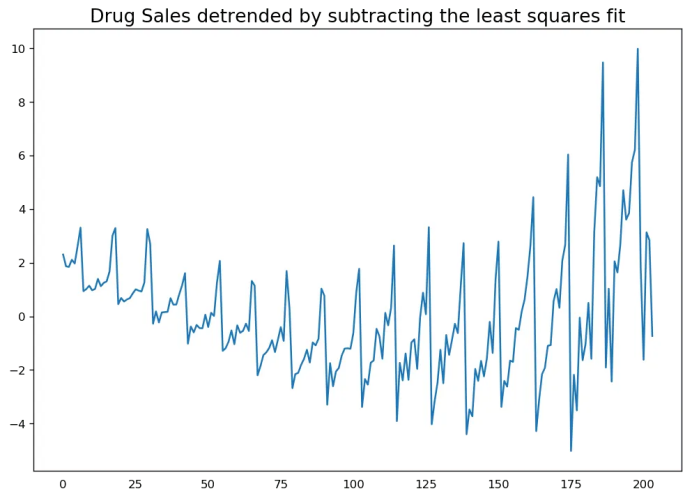
detrended = signal.detrend(df.value.values)
plt.plot(detrended)
plt.title('Drug Sales detrended by subtracting the least squares fit', fontsize=16)
# Using statmodels: Subtracting the Trend Component.
from statsmodels.tsa.seasonal import seasonal_decompose
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
detrended = df.value.values - result_mul.trend
plt.plot(detrended)
plt.title('Drug Sales detrended by subtracting the trend component', fontsize=16)
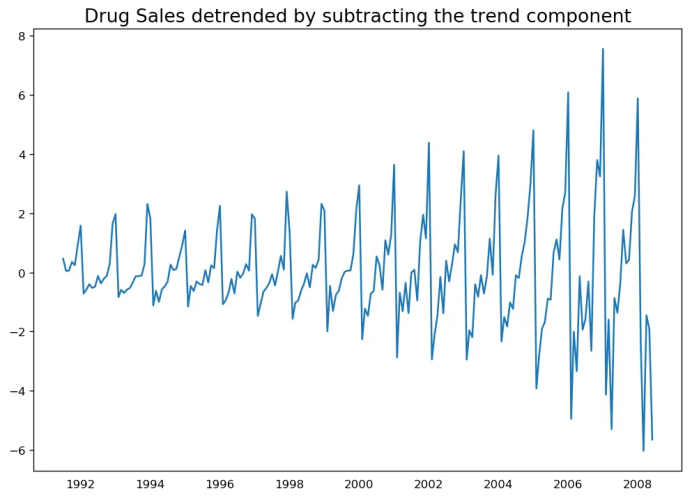
13. 怎樣對時間序列去季節(jié)化?
1. 取一個以長度為季節(jié)窗口的移動平均線。這將在這個過程中使序列變得平滑； 2. 序列季節(jié)性差分（從當前值當中減去前一季節(jié)的值）； 3. 將序列值除以從STL分解當中獲得的季節(jié)性指數(shù)。
如果除以季節(jié)性指數(shù)后仍沒辦法得到良好的結果，再試一下序列對數(shù)轉換然后再做。你之后可以通過去指數(shù)恢復到原始尺度。
# Subtracting the Trend Component.
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')
# Time Series Decomposition
result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')
# Deseasonalize
deseasonalized = df.value.values / result_mul.seasonal
# Plot
plt.plot(deseasonalized)
plt.title('Drug Sales Deseasonalized', fontsize=16)
plt.plot()
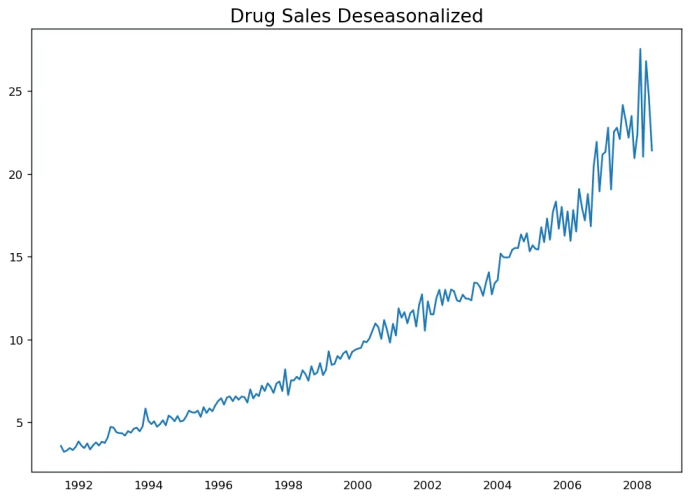
14. 怎樣檢驗時間序列的季節(jié)性？
1. 一天的每個小時； 2. 一月的每天； 3. 每周； 4. 每月； 5. 每年。
然而，如果你想要一個更權威的季節(jié)性檢驗，使用自回歸函數(shù)（ACF）圖。更多關于自回歸的信息將在下一部分介紹。但是當強季節(jié)性模式出現(xiàn)時，ACF圖通常揭示了在季節(jié)窗的倍數(shù)處明顯的重復峰值。
例如，藥品銷售時間序列是每年都有重復模式的一個月度序列。所以，你可以看到第12,24和36條線等的峰值。
我必須警告你在現(xiàn)實世界的數(shù)據(jù)集當中，這樣強的模式很難見到，并且有可能被各種噪音所扭曲，所以你需要一雙仔細的眼睛來捕獲這些模式。
from pandas.plotting import autocorrelation_plot
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
plt.rcParams.update({'figure.figsize':(9,5), 'figure.dpi':120})
autocorrelation_plot(df.value.tolist())
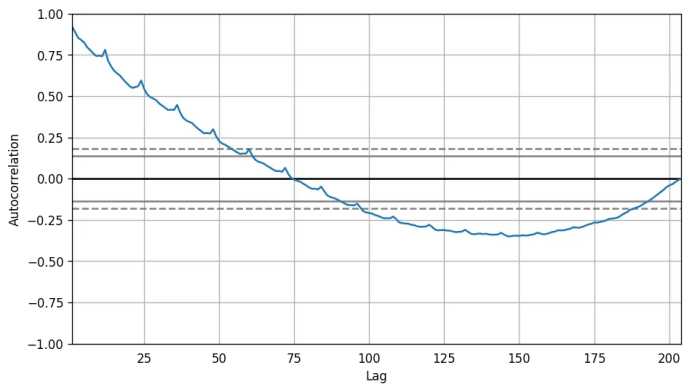
除此之外，如果你想做統(tǒng)計檢驗，CHT檢驗可以檢驗季節(jié)性差異是否對序列平穩(wěn)化有必要。
15. 如何處理時間序列當中的缺失值？
其次，當處理時間序列時，你通常不應該用序列均值來替代缺失值，尤其是序列非平穩(wěn)的時候，一個快捷粗略的處理方法來說你應該做的是向前填充之前的值。
然而，依賴于序列的本質，你想要在得出結論之前嘗試多種方法。有效的缺失值處理方法有：
-
向后填充；
-
線性內插；
-
二次內插；
-
最鄰近平均值；
-
對應季節(jié)的平均值。
為了衡量缺失值的表現(xiàn)，我在時間序列當中手動引入缺失值，使用上述方法處理并衡量處理值和真實值之間的均方誤差。
# # Generate dataset
from scipy.interpolate import interp1d
from sklearn.metrics import mean_squared_error
df_orig = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date').head(100)
df = pd.read_csv('datasets/a10_missings.csv', parse_dates=['date'], index_col='date')
fig, axes = plt.subplots(7, 1, sharex=True, figsize=(10, 12))
plt.rcParams.update({'xtick.bottom' : False})
## 1. Actual -------------------------------
df_orig.plot(title='Actual', ax=axes[0], label='Actual', color='red', style=".-")
df.plot(title='Actual', ax=axes[0], label='Actual', color='green', style=".-")
axes[0].legend(["Missing Data", "Available Data"])
## 2. Forward Fill --------------------------
df_ffill = df.ffill()
error = np.round(mean_squared_error(df_orig['value'], df_ffill['value']), 2)
df_ffill['value'].plot(title='Forward Fill (MSE: ' + str(error) +")", ax=axes[1], label='Forward Fill', style=".-")
## 3. Backward Fill -------------------------
df_bfill = df.bfill()
error = np.round(mean_squared_error(df_orig['value'], df_bfill['value']), 2)
df_bfill['value'].plot(title="Backward Fill (MSE: " + str(error) +")", ax=axes[2], label='Back Fill', color='firebrick', style=".-")
## 4. Linear Interpolation ------------------
df['rownum'] = np.arange(df.shape[0])
df_nona = df.dropna(subset = ['value'])
f = interp1d(df_nona['rownum'], df_nona['value'])
df['linear_fill'] = f(df['rownum'])
error = np.round(mean_squared_error(df_orig['value'], df['linear_fill']), 2)
df['linear_fill'].plot(title="Linear Fill (MSE: " + str(error) +")", ax=axes[3], label='Cubic Fill', color='brown', style=".-")
## 5. Cubic Interpolation --------------------
f2 = interp1d(df_nona['rownum'], df_nona['value'], kind='cubic')
df['cubic_fill'] = f2(df['rownum'])
error = np.round(mean_squared_error(df_orig['value'], df['cubic_fill']), 2)
df['cubic_fill'].plot(title="Cubic Fill (MSE: " + str(error) +")", ax=axes[4], label='Cubic Fill', color='red', style=".-")
# Interpolation References:
# https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html
# https://docs.scipy.org/doc/scipy/reference/interpolate.html
## 6. Mean of 'n' Nearest Past Neighbors ------
def knn_mean(ts, n):
out = np.copy(ts)
for i, val in enumerate(ts):
if np.isnan(val):
n_by_2 = np.ceil(n/2)
lower = np.max([0, int(i-n_by_2)])
upper = np.min([len(ts)+1, int(i+n_by_2)])
ts_near = np.concatenate([ts[lower:i], ts[i:upper]])
out[i] = np.nanmean(ts_near)
return out
df['knn_mean'] = knn_mean(df.value.values, 8)
error = np.round(mean_squared_error(df_orig['value'], df['knn_mean']), 2)
df['knn_mean'].plot(title="KNN Mean (MSE: " + str(error) +")", ax=axes[5], label='KNN Mean', color='tomato', alpha=0.5, style=".-")
## 7. Seasonal Mean ----------------------------
def seasonal_mean(ts, n, lr=0.7):
"""
Compute the mean of corresponding seasonal periods
ts: 1D array-like of the time series
n: Seasonal window length of the time series
"""
out = np.copy(ts)
for i, val in enumerate(ts):
if np.isnan(val):
ts_seas = ts[i-1::-n] # previous seasons only
if np.isnan(np.nanmean(ts_seas)):
ts_seas = np.concatenate([ts[i-1::-n], ts[i::n]]) # previous and forward
out[i] = np.nanmean(ts_seas) * lr
return out
df['seasonal_mean'] = seasonal_mean(df.value, n=12, lr=1.25)
error = np.round(mean_squared_error(df_orig['value'], df['seasonal_mean']), 2)
df['seasonal_mean'].plot(title="Seasonal Mean (MSE: " + str(error) +")", ax=axes[6], label='Seasonal Mean', color='blue', alpha=0.5, style=".-")
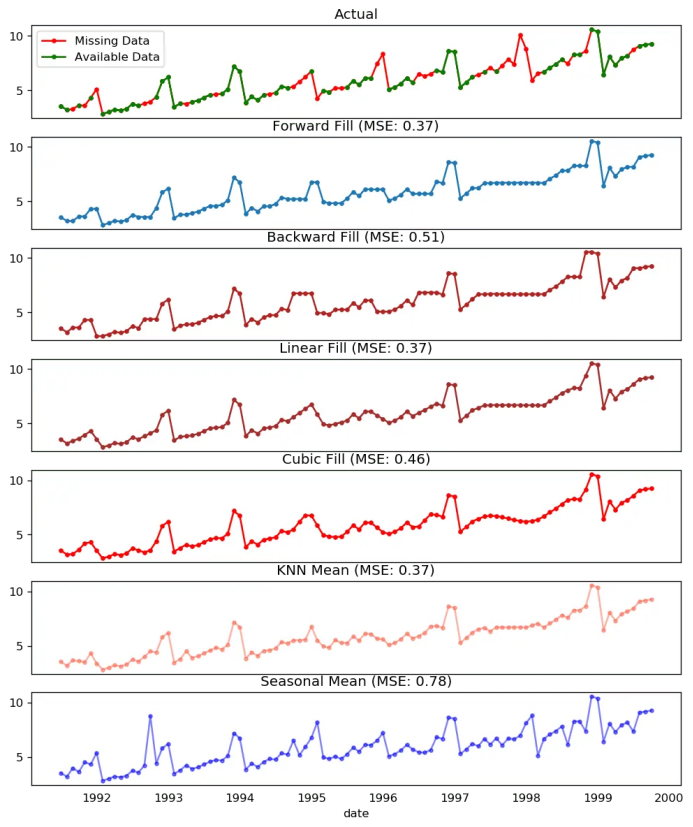?缺失值處理
1. 如果你有解釋變量，可以使用像隨機森林或k-鄰近算法的預測模型來預測它。 2. 如果你有足夠多的過去觀測值，可以預測缺失值。 3. 如果你有足夠的未來觀測值，回測缺失值。 4. 從之前的周期預測相對應的部分。
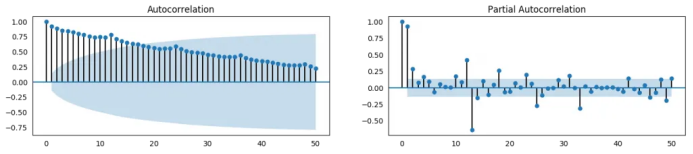
16. 什么是自相關和偏自相關函數(shù)？
偏自相關也會傳遞相似的信息但是它傳遞的是序列和它滯后量的純粹相關，排除了其他中間滯后量對相關的貢獻。
from statsmodels.tsa.stattools import acf, pacf
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
fig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)
plot_acf(df.value.tolist(), lags=50, ax=axes[0])
plot_pacf(df.value.tolist(), lags=50, ax=axes[1])
17. 怎樣計算偏自相關函數(shù)?
序列滯后量（k）的偏自相關是Y的自回歸方程中滯后量的系數(shù)。Y的自回歸方程就是Y及其滯后量作為預測項的線性回歸。
For Example, if?Y_t?is the current series and?Y_t-1?is the lag 1 of?Y, then the partial autocorrelation of lag 3 (Y_t-3) is the coefficient $\alpha_3$ of?Y_t-3?in the following equation: 例如，如果Y_t是當前的序列，Y_t-1是Y的滯后量1，那么滯后量3（Y_t-3）的偏自相關就是下面方程中Y_t-3的系數(shù)
:
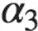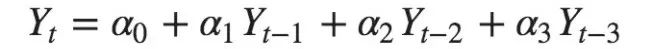
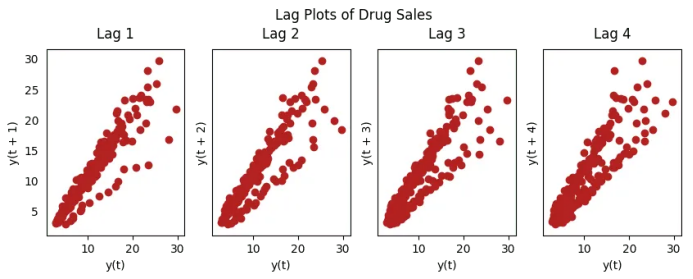
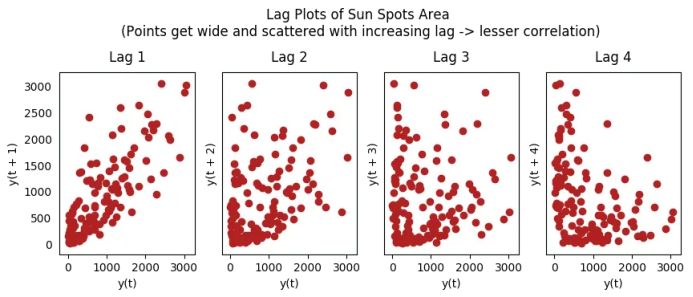
18. 滯后圖
在下面太陽黑子面積時間序列的例子當中，隨著n_lag增加，圖越來越分散。
from pandas.plotting import lag_plot
plt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})
# Import
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
# Plot
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)
fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)
for i, ax in enumerate(axes.flatten()[:4]):
lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick')
ax.set_title('Lag ' + str(i+1))
fig.suptitle('Lag Plots of Drug Sales', y=1.05)
plt.show()
?
19. 怎樣估計時間序列的預測能力?
近似熵越高，預測越難。另一個更好的選項是“樣本熵”。
樣本熵類似與近似熵，但是在估計小時間序列的復雜性上結果更一致。例如，較少樣本點的隨機時間序列 “近似熵”可能比一個更規(guī)律的時間序列更低，然而更長的時間序列可能會有一個更高的“近似熵”。
樣本熵可以很好地處理這個問題。請看如下演示：
# https://en.wikipedia.org/wiki/Approximate_entropy
ss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')
a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')
rand_small = np.random.randint(0, 100, size=36)
rand_big = np.random.randint(0, 100, size=136)
def ApEn(U, m, r):
"""Compute Aproximate entropy"""
def _maxdist(x_i, x_j):
return max([abs(ua - va) for ua, va in zip(x_i, x_j)])
def _phi(m):
x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x]
return (N - m + 1.0)**(-1) * sum(np.log(C))
N = len(U)
return abs(_phi(m+1) - _phi(m))
print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.651
print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.537
print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143
print(ApEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 0.716
0.6514704970333534
0.5374775224973489
0.0898376940798844
0.7369242960384561
# https://en.wikipedia.org/wiki/Sample_entropy
def SampEn(U, m, r):
"""Compute Sample entropy"""
def _maxdist(x_i, x_j):
return max([abs(ua - va) for ua, va in zip(x_i, x_j)])
def _phi(m):
x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]
C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))]
return sum(C)
N = len(U)
return -np.log(_phi(m+1) / _phi(m))
print(SampEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.78
print(SampEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.41
print(SampEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 1.79
print(SampEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 2.42
0.7853311366380039
0.41887013457621214
inf
2.181224235989778
del sys.path[0]
20. 為何要以及怎樣對時間序列進行平滑處理?
-
在信號當中減小噪聲的影響從而得到一個經過噪聲濾波的序列近似。
-
平滑版的序列可用于解釋原始序列本身的特征。
-
趨勢更好地可視化。
怎樣對序列平滑處理？ 讓我們討論一下以下方法：
1. 使用移動平均； 2. 做LOESS光滑（局部回歸）； 3.?做LOWESS光滑（局部加權回歸）。
移動均值就是定義寬度的滾動窗口的均值。但是你必須明智地選擇窗口寬度，因為大范圍窗口可能會造成序列過度平滑。例如，窗口大小等于季節(jié)持續(xù)時間時（例如：12為月度序列），將有效地抵消季節(jié)效應。
LOESS，局部回歸的簡寫，適應于每個點鄰近的多元回歸。可通過statsmodels包使用，你可以使用frac參數(shù)確定被納入擬合回歸模型的鄰近數(shù)據(jù)點的百分比來控制平滑度。
下載數(shù)據(jù)集:?Elecequip.csv
from statsmodels.nonparametric.smoothers_lowess import lowess
plt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})
df_orig = pd.read_csv('datasets/elecequip.csv', parse_dates=['date'], index_col='date')
df_ma = df_orig.value.rolling(3, center=True, closed='both').mean()
df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])
df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])
fig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)
df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')
df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')
df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')
df_ma.plot(ax=axes[3], title='Moving Average (3)')
fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)
plt.show()
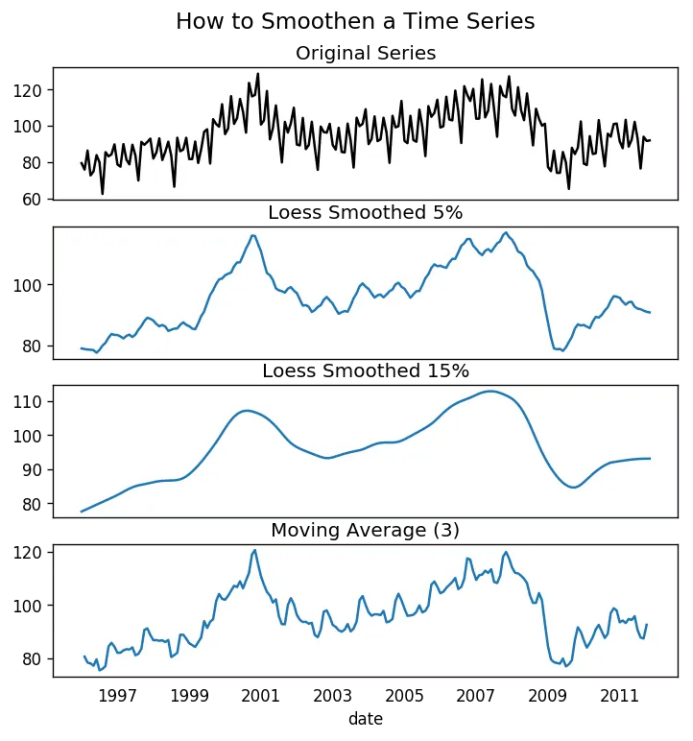
21. 如何使用Granger因果檢驗得知是否一個時間序列有助于預測另一個序列？
? Granger因果檢驗被用于檢驗是否一個時間序列可以預測另一個序列。 Granger因果檢驗是如何工作 的？它基于如果X引起Y的變化，Y基于之前的Y值和之前的X值的預測效果要優(yōu)于僅基于之前的Y值的預測效果。
所以需要了解Granger因果檢驗不能應用于Y的滯后量引起Y自身的變化的情況，而通常僅用于外源變量（不是Y的滯后量）。
它在statsmodel包中得到了很好的實現(xiàn)。 它采納2列數(shù)據(jù)的二維數(shù)組作為主要參數(shù)，被預測值是第一列，而預測變量（X）在第二列。
零假設檢驗：第二列的序列不能Granger預測第一列數(shù)據(jù)。如果p值小于顯著性水平（0.05），你可以拒絕零假設并得出結論：X的滯后量確實有用。
第二個參數(shù)maxlag決定有多少Y的滯后量應該納入檢驗當中。
from statsmodels.tsa.stattools import grangercausalitytests
df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])
= df.date.dt.month
'month']], maxlag=2)
Granger Causality
number of lags (no zero) 1
ssr based F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1
ssr based chi2 test: chi2=55.6014 , p=0.0000 , df=1
likelihood ratio test: chi2=49.1426 , p=0.0000 , df=1
parameter F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1
Granger Causality
number of lags (no zero) 2
ssr based F test: F=162.6989, p=0.0000 , df_denom=197, df_num=2
ssr based chi2 test: chi2=333.6567, p=0.0000 , df=2
likelihood ratio test: chi2=196.9956, p=0.0000 , df=2
parameter F test: F=162.6989, p=0.0000 , df_denom=197, df_num=2
在上述例子當中， 實際上所有檢驗的p值只能無限接近于0 。所以“月份”實際上可以用于預測航空乘客的數(shù)量。
22. 下一步是什么？
在下一篇文章當中，我將帶你了解使用ARIMA ?（Autoregressive Integrated Moving Average，自回歸求和移動平均模式）建立時間序列預測模型的深度過程。下次再見。 ?
原文標題：
Time Series Analysis in Python – A Comprehensive Guide with Examples
原文鏈接：
https://www.machinelearningplus.com/time-series/time-series-analysis-python/
編輯：黃繼彥
評論
圖片
表情