Python時間序列分析指南!
本文約7500字,建議閱讀20+分鐘
本文介紹了時間序列的定義、特征并結(jié)合實例給出了時間序列在Python中評價指標(biāo)和方法。
時間序列是在規(guī)律性時間間隔上記錄的觀測值序列。本指南將帶你了解在Python中分析給定時間序列的特征的全過程。
1. 什么是時間序列?
2. 如何在Python中導(dǎo)入時間序列?
3. 什么是面板數(shù)據(jù)?
4. 時間序列可視化
5. 時間序列的模式
6. 時間序列的加法和乘法
7. 如何將時間序列分解?
8. 平穩(wěn)和非平穩(wěn)時間序列
9. 如何獲取平穩(wěn)的時間序列?
10. 如何檢驗平穩(wěn)性?
11. 白噪音和平穩(wěn)序列的差異是什么?
12. 如何去除時間序列的線性分量?
13. 如何消除時間序列的季節(jié)性?
14. 如何檢驗時間序列的季節(jié)性?
15. 如何處理時間序列中的缺失值?
16. 什么是自回歸和偏自回歸函數(shù)?
17. 如何計算偏自回歸函數(shù)?
18. 滯后圖
19. 如何估計時間序列的預(yù)測能力?
20. 為什么以及怎樣使時間序列平滑?
21. 如何使用Granger因果檢驗來獲知時間序列是否對預(yù)測另一個序列幫助?
22. 下一步是什么?
2. 如何在Python中導(dǎo)入時間序列?
from dateutil.parser import parseimport matplotlib as mplimport matplotlib.pyplot as pltimport seaborn as snsimport numpy as npimport pandas as pdplt.rcParams.update({'figure.figsize': (10, 7), 'figure.dpi': 120})# Import as Dataframedf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])df.head()
ser = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')ser.head()
# dataset source: https://github.com/rouseguydf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/MarketArrivals.csv')df = df.loc[df.market=='MUMBAI', :]df.head()
4. 時間序列可視化
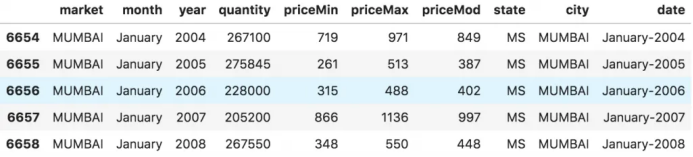
# Time series data source: fpp pacakge in R.import matplotlib.pyplot as pltdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')# Draw Plotdef plot_df(df, x, y, title="", xlabel='Date', ylabel='Value', dpi=100):plt.figure(figsize=(16,5), dpi=dpi)plt.plot(x, y, color='tab:red')plt.gca().set(title=title, xlabel=xlabel, ylabel=ylabel)plt.show()plot_df(df, x=df.index, y=df.value, title='Monthly anti-diabetic drug sales in Australia from 1992 to 2008.')
 時間序列可視化
時間序列可視化
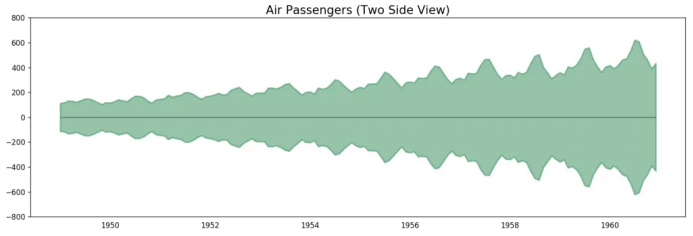
# Import datadf = pd.read_csv('datasets/AirPassengers.csv', parse_dates=['date'])x = df['date'].valuesy1 = df['value'].values# Plotfig, ax = plt.subplots(1, 1, figsize=(16,5), dpi= 120)plt.fill_between(x, y1=y1, y2=-y1, alpha=0.5, linewidth=2, color='seagreen')plt.ylim(-800, 800)plt.title('Air Passengers (Two Side View)', fontsize=16)plt.hlines(y=0, xmin=np.min(df.date), xmax=np.max(df.date), linewidth=.5)plt.show()
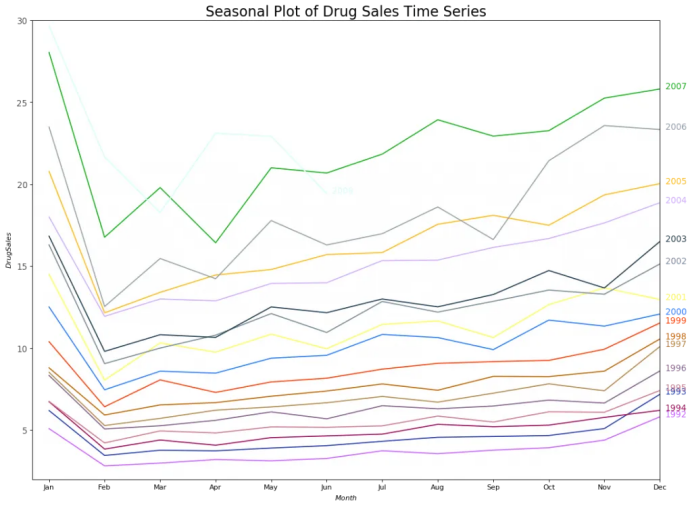
# Import Datadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')df.reset_index(inplace=True)# Prepare datadf['year'] = [d.year for d in df.date]df['month'] = [d.strftime('%b') for d in df.date]years = df['year'].unique()# Prep Colorsnp.random.seed(100)mycolors = np.random.choice(list(mpl.colors.XKCD_COLORS.keys()), len(years), replace=False)# Draw Plotplt.figure(figsize=(16,12), dpi= 80)for i, y in enumerate(years):if i > 0:plt.plot('month', 'value', data=df.loc[df.year==y, :], color=mycolors[i], label=y)plt.text(df.loc[df.year==y, :].shape[0]-.9, df.loc[df.year==y, 'value'][-1:].values[0], y, fontsize=12, color=mycolors[i])# Decorationplt.gca().set(xlim=(-0.3, 11), ylim=(2, 30), ylabel='$Drug Sales$', xlabel='$Month$')plt.yticks(fontsize=12, alpha=.7)plt.title("Seasonal Plot of Drug Sales Time Series", fontsize=20)plt.show()
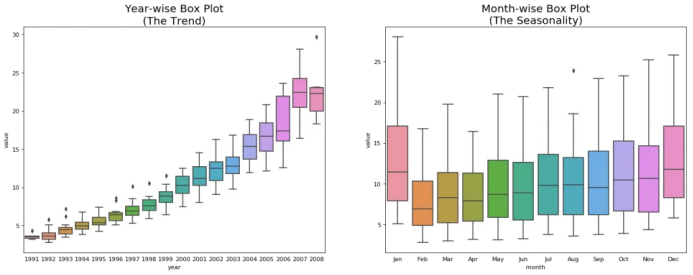
# Import Datadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')df.reset_index(inplace=True)# Prepare datadf['year'] = [d.year for d in df.date]df['month'] = [d.strftime('%b') for d in df.date]years = df['year'].unique()# Draw Plotfig, axes = plt.subplots(1, 2, figsize=(20,7), dpi= 80)sns.boxplot(x='year', y='value', data=df, ax=axes[0])sns.boxplot(x='month', y='value', data=df.loc[~df.year.isin([1991, 2008]), :])# Set Titleaxes[0].set_title('Year-wise Box Plot\n(The Trend)', fontsize=18);axes[1].set_title('Month-wise Box Plot\n(The Seasonality)', fontsize=18)plt.show()
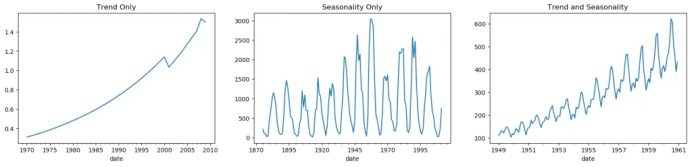
5. 時間序列的模式
fig, axes = plt.subplots(1,3, figsize=(20,4), dpi=100)pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/guinearice.csv', parse_dates=['date'], index_col='date').plot(title='Trend Only', legend=False, ax=axes[0])pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv', parse_dates=['date'], index_col='date').plot(title='Seasonality Only', legend=False, ax=axes[1])pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/AirPassengers.csv', parse_dates=['date'], index_col='date').plot(title='Trend and Seasonality', legend=False, ax=axes[2])
6. 時間序列的加法和乘法
7. 怎樣分解時間序列的成分?
from statsmodels.tsa.seasonal import seasonal_decomposefrom dateutil.parser import parse# Import Datadf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')# Multiplicative Decompositionresult_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')# Additive Decompositionresult_add = seasonal_decompose(df['value'], model='additive', extrapolate_trend='freq')# Plotplt.rcParams.update({'figure.figsize': (10,10)})result_mul.plot().suptitle('Multiplicative Decompose', fontsize=22)result_add.plot().suptitle('Additive Decompose', fontsize=22)plt.show()
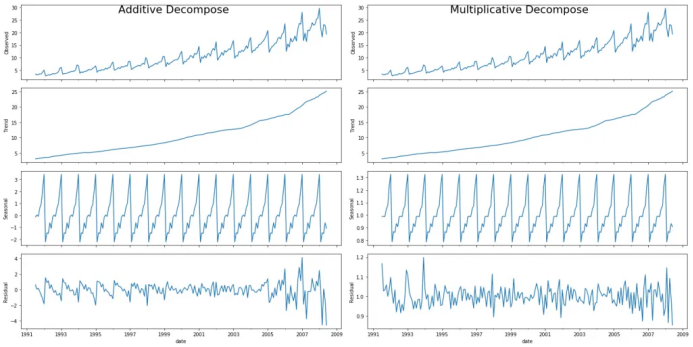
# Extract the Components ----# Actual Values = Product of (Seasonal * Trend * Resid)df_reconstructed = pd.concat([result_mul.seasonal, result_mul.trend, result_mul.resid, result_mul.observed], axis=1)df_reconstructed.columns = ['seas', 'trend', 'resid', 'actual_values']df_reconstructed.head()
8. 平穩(wěn)和非平穩(wěn)時間序列
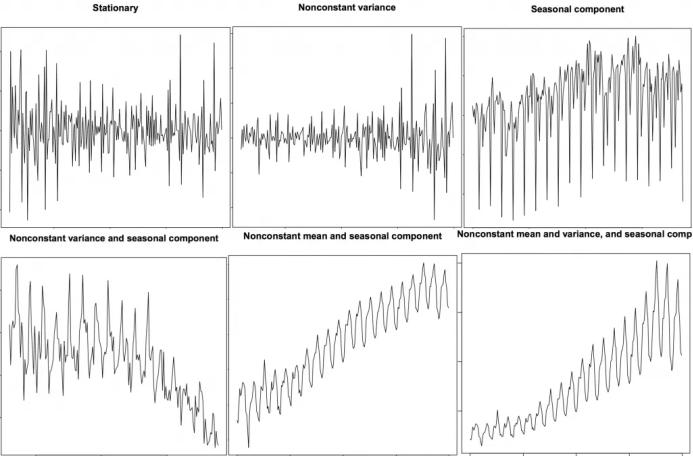
9. 如何獲取平穩(wěn)的時間序列?
9.2 為什么要在預(yù)測之前將非平穩(wěn)數(shù)據(jù)平穩(wěn)化?
10. 怎樣檢驗平穩(wěn)性?
from statsmodels.tsa.stattools import adfuller, kpssdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])# ADF Testresult = adfuller(df.value.values, autolag='AIC')print(f'ADF Statistic: {result[0]}')print(f'p-value: {result[1]}')for key, value in result[4].items():print('Critial Values:')print(f' {key}, {value}')# KPSS Testresult = kpss(df.value.values, regression='c')print('\nKPSS Statistic: %f' % result[0])print('p-value: %f' % result[1])for key, value in result[3].items():print('Critial Values:')print(f' {key}, {value}')ADF Statistic: 3.14518568930674p-value: 1.0Critial Values:1%, -3.465620397124192Critial Values:5%, -2.8770397560752436Critial Values:10%, -2.5750324547306476KPSS Statistic: 1.313675p-value: 0.010000Critial Values:10%, 0.347Critial Values:5%, 0.463Critial Values:2.5%, 0.574Critial Values:1%, 0.739
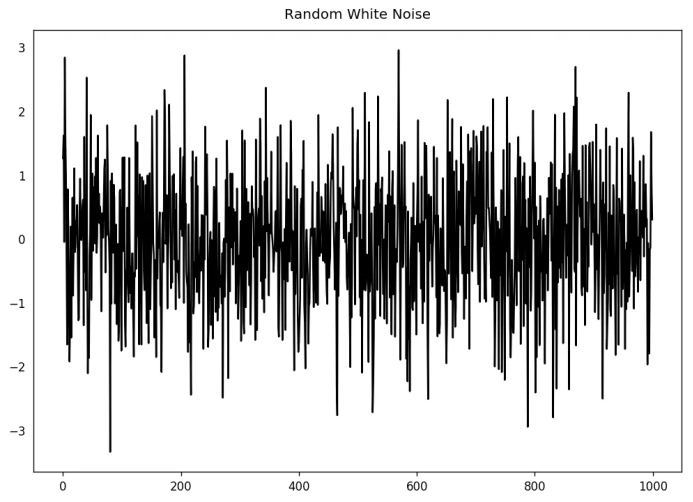
11. 白噪音和平穩(wěn)序列的差異是什么?
randvals = np.random.randn(1000)pd.Series(randvals).plot(title='Random White Noise', color='k')
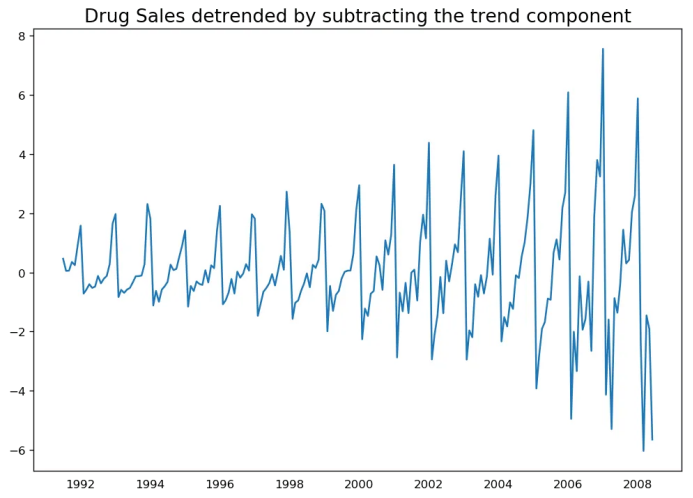
12. 怎樣將時間序列去趨勢化?
# Using scipy: Subtract the line of best fitfrom scipy import signaldf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])detrended = signal.detrend(df.value.values)plt.plot(detrended)plt.title('Drug Sales detrended by subtracting the least squares fit', fontsize=16)

# Using statmodels: Subtracting the Trend Component.from statsmodels.tsa.seasonal import seasonal_decomposedf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')result_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')detrended = df.value.values - result_mul.trendplt.plot(detrended)plt.title('Drug Sales detrended by subtracting the trend component', fontsize=16)
13. 怎樣對時間序列去季節(jié)化?
# Subtracting the Trend Component.df = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date')# Time Series Decompositionresult_mul = seasonal_decompose(df['value'], model='multiplicative', extrapolate_trend='freq')# Deseasonalizedeseasonalized = df.value.values / result_mul.seasonal# Plotplt.plot(deseasonalized)plt.title('Drug Sales Deseasonalized', fontsize=16)plt.plot()

14. 怎樣檢驗時間序列的季節(jié)性?
from pandas.plotting import autocorrelation_plotdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Draw Plotplt.rcParams.update({'figure.figsize':(9,5), 'figure.dpi':120})autocorrelation_plot(df.value.tolist())

15. 如何處理時間序列當(dāng)中的缺失值?
向后填充;
線性內(nèi)插;
二次內(nèi)插;
最鄰近平均值;
對應(yīng)季節(jié)的平均值。
# # Generate datasetfrom scipy.interpolate import interp1dfrom sklearn.metrics import mean_squared_errordf_orig = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'], index_col='date').head(100)df = pd.read_csv('datasets/a10_missings.csv', parse_dates=['date'], index_col='date')fig, axes = plt.subplots(7, 1, sharex=True, figsize=(10, 12))plt.rcParams.update({'xtick.bottom' : False})## 1. Actual -------------------------------df_orig.plot(title='Actual', ax=axes[0], label='Actual', color='red', style=".-")df.plot(title='Actual', ax=axes[0], label='Actual', color='green', style=".-")axes[0].legend(["Missing Data", "Available Data"])## 2. Forward Fill --------------------------df_ffill = df.ffill()error = np.round(mean_squared_error(df_orig['value'], df_ffill['value']), 2)df_ffill['value'].plot(title='Forward Fill (MSE: ' + str(error) +")", ax=axes[1], label='Forward Fill', style=".-")## 3. Backward Fill -------------------------df_bfill = df.bfill()error = np.round(mean_squared_error(df_orig['value'], df_bfill['value']), 2)df_bfill['value'].plot(title="Backward Fill (MSE: " + str(error) +")", ax=axes[2], label='Back Fill', color='firebrick', style=".-")## 4. Linear Interpolation ------------------df['rownum'] = np.arange(df.shape[0])df_nona = df.dropna(subset = ['value'])f = interp1d(df_nona['rownum'], df_nona['value'])df['linear_fill'] = f(df['rownum'])error = np.round(mean_squared_error(df_orig['value'], df['linear_fill']), 2)df['linear_fill'].plot(title="Linear Fill (MSE: " + str(error) +")", ax=axes[3], label='Cubic Fill', color='brown', style=".-")## 5. Cubic Interpolation --------------------f2 = interp1d(df_nona['rownum'], df_nona['value'], kind='cubic')df['cubic_fill'] = f2(df['rownum'])error = np.round(mean_squared_error(df_orig['value'], df['cubic_fill']), 2)df['cubic_fill'].plot(title="Cubic Fill (MSE: " + str(error) +")", ax=axes[4], label='Cubic Fill', color='red', style=".-")# Interpolation References:# https://docs.scipy.org/doc/scipy/reference/tutorial/interpolate.html# https://docs.scipy.org/doc/scipy/reference/interpolate.html## 6. Mean of 'n' Nearest Past Neighbors ------def knn_mean(ts, n):out = np.copy(ts)for i, val in enumerate(ts):if np.isnan(val):n_by_2 = np.ceil(n/2)lower = np.max([0, int(i-n_by_2)])upper = np.min([len(ts)+1, int(i+n_by_2)])ts_near = np.concatenate([ts[lower:i], ts[i:upper]])out[i] = np.nanmean(ts_near)return outdf['knn_mean'] = knn_mean(df.value.values, 8)error = np.round(mean_squared_error(df_orig['value'], df['knn_mean']), 2)df['knn_mean'].plot(title="KNN Mean (MSE: " + str(error) +")", ax=axes[5], label='KNN Mean', color='tomato', alpha=0.5, style=".-")## 7. Seasonal Mean ----------------------------def seasonal_mean(ts, n, lr=0.7):"""Compute the mean of corresponding seasonal periodsts: 1D array-like of the time seriesn: Seasonal window length of the time series"""out = np.copy(ts)for i, val in enumerate(ts):if np.isnan(val):ts_seas = ts[i-1::-n] # previous seasons onlyif np.isnan(np.nanmean(ts_seas)):ts_seas = np.concatenate([ts[i-1::-n], ts[i::n]]) # previous and forwardout[i] = np.nanmean(ts_seas) * lrreturn outdf['seasonal_mean'] = seasonal_mean(df.value, n=12, lr=1.25)error = np.round(mean_squared_error(df_orig['value'], df['seasonal_mean']), 2)df['seasonal_mean'].plot(title="Seasonal Mean (MSE: " + str(error) +")", ax=axes[6], label='Seasonal Mean', color='blue', alpha=0.5, style=".-")
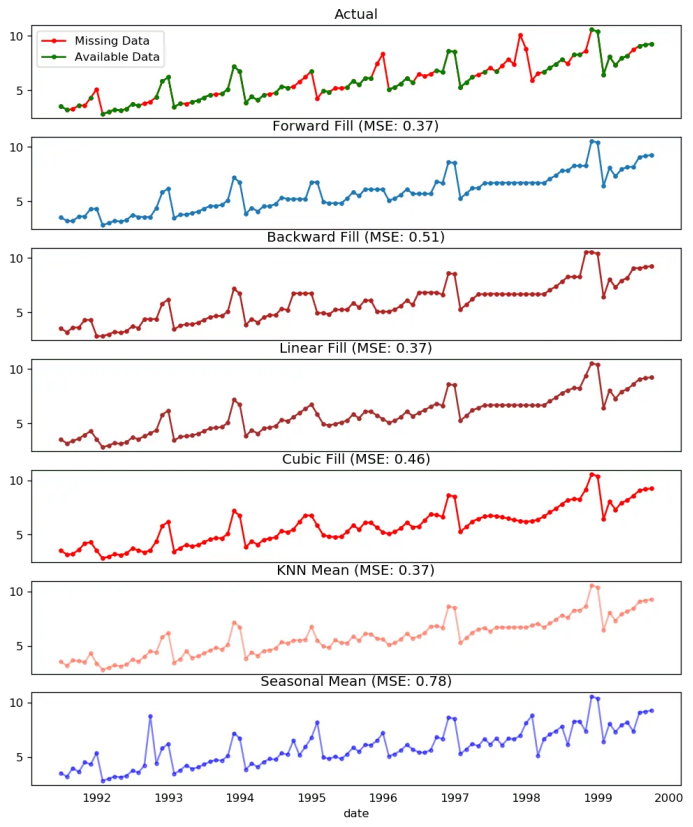 缺失值處理
缺失值處理
16. 什么是自相關(guān)和偏自相關(guān)函數(shù)?
from statsmodels.tsa.stattools import acf, pacffrom statsmodels.graphics.tsaplots import plot_acf, plot_pacfdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Calculate ACF and PACF upto 50 lags# acf_50 = acf(df.value, nlags=50)# pacf_50 = pacf(df.value, nlags=50)# Draw Plotfig, axes = plt.subplots(1,2,figsize=(16,3), dpi= 100)plot_acf(df.value.tolist(), lags=50, ax=axes[0])plot_pacf(df.value.tolist(), lags=50, ax=axes[1])
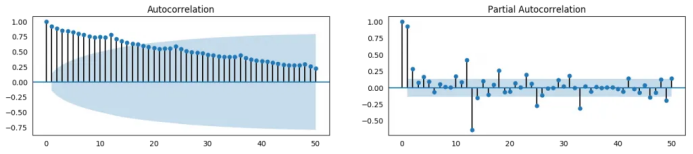
17. 怎樣計算偏自相關(guān)函數(shù)?
18. 滯后圖
from pandas.plotting import lag_plotplt.rcParams.update({'ytick.left' : False, 'axes.titlepad':10})# Importss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')# Plotfig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):lag_plot(ss.value, lag=i+1, ax=ax, c='firebrick')ax.set_title('Lag ' + str(i+1))fig.suptitle('Lag Plots of Sun Spots Area \n(Points get wide and scattered with increasing lag -> lesser correlation)\n', y=1.15)fig, axes = plt.subplots(1, 4, figsize=(10,3), sharex=True, sharey=True, dpi=100)for i, ax in enumerate(axes.flatten()[:4]):lag_plot(a10.value, lag=i+1, ax=ax, c='firebrick')ax.set_title('Lag ' + str(i+1))fig.suptitle('Lag Plots of Drug Sales', y=1.05)plt.show()
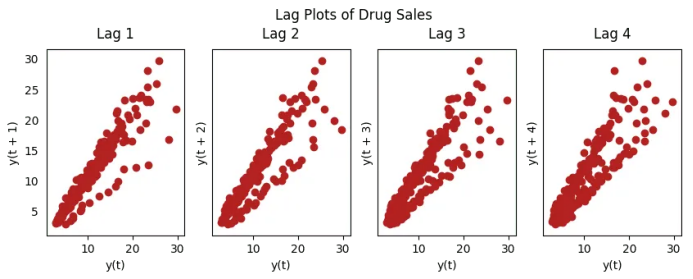

19. 怎樣估計時間序列的預(yù)測能力?
# https://en.wikipedia.org/wiki/Approximate_entropyss = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/sunspotarea.csv')a10 = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv')rand_small = np.random.randint(0, 100, size=36)rand_big = np.random.randint(0, 100, size=136)def ApEn(U, m, r):"""Compute Aproximate entropy"""def _maxdist(x_i, x_j):return max([abs(ua - va) for ua, va in zip(x_i, x_j)])def _phi(m):x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]C = [len([1 for x_j in x if _maxdist(x_i, x_j) <= r]) / (N - m + 1.0) for x_i in x]return (N - m + 1.0)**(-1) * sum(np.log(C))N = len(U)return abs(_phi(m+1) - _phi(m))print(ApEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.651print(ApEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.537print(ApEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 0.143print(ApEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 0.7160.65147049703335340.53747752249734890.08983769407988440.7369242960384561# https://en.wikipedia.org/wiki/Sample_entropydef SampEn(U, m, r):"""Compute Sample entropy"""def _maxdist(x_i, x_j):return max([abs(ua - va) for ua, va in zip(x_i, x_j)])def _phi(m):x = [[U[j] for j in range(i, i + m - 1 + 1)] for i in range(N - m + 1)]C = [len([1 for j in range(len(x)) if i != j and _maxdist(x[i], x[j]) <= r]) for i in range(len(x))]return sum(C)N = len(U)return -np.log(_phi(m+1) / _phi(m))print(SampEn(ss.value, m=2, r=0.2*np.std(ss.value))) # 0.78print(SampEn(a10.value, m=2, r=0.2*np.std(a10.value))) # 0.41print(SampEn(rand_small, m=2, r=0.2*np.std(rand_small))) # 1.79print(SampEn(rand_big, m=2, r=0.2*np.std(rand_big))) # 2.420.78533113663800390.41887013457621214inf2.181224235989778del sys.path[0]
20. 為何要以及怎樣對時間序列進(jìn)行平滑處理?
在信號當(dāng)中減小噪聲的影響從而得到一個經(jīng)過噪聲濾波的序列近似。
平滑版的序列可用于解釋原始序列本身的特征。
趨勢更好地可視化。
from statsmodels.nonparametric.smoothers_lowess import lowessplt.rcParams.update({'xtick.bottom' : False, 'axes.titlepad':5})# Importdf_orig = pd.read_csv('datasets/elecequip.csv', parse_dates=['date'], index_col='date')# 1. Moving Averagedf_ma = df_orig.value.rolling(3, center=True, closed='both').mean()# 2. Loess Smoothing (5% and 15%)df_loess_5 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.05)[:, 1], index=df_orig.index, columns=['value'])df_loess_15 = pd.DataFrame(lowess(df_orig.value, np.arange(len(df_orig.value)), frac=0.15)[:, 1], index=df_orig.index, columns=['value'])# Plotfig, axes = plt.subplots(4,1, figsize=(7, 7), sharex=True, dpi=120)df_orig['value'].plot(ax=axes[0], color='k', title='Original Series')df_loess_5['value'].plot(ax=axes[1], title='Loess Smoothed 5%')df_loess_15['value'].plot(ax=axes[2], title='Loess Smoothed 15%')df_ma.plot(ax=axes[3], title='Moving Average (3)')fig.suptitle('How to Smoothen a Time Series', y=0.95, fontsize=14)plt.show()
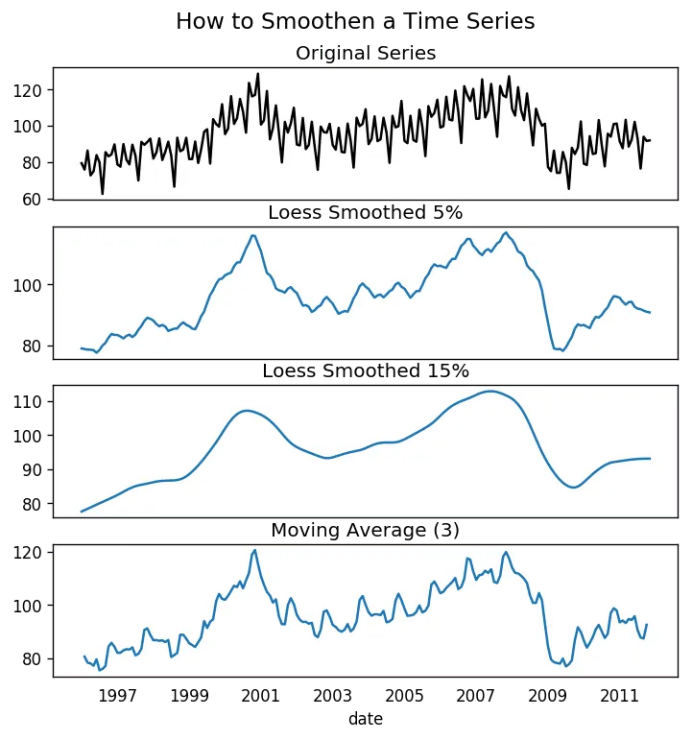
21. 如何使用Granger因果檢驗得知是否一個時間序列有助于預(yù)測另一個序列?
from statsmodels.tsa.stattools import grangercausalitytestsdf = pd.read_csv('https://raw.githubusercontent.com/selva86/datasets/master/a10.csv', parse_dates=['date'])df['month'] = df.date.dt.monthgrangercausalitytests(df[['value', 'month']], maxlag=2)Granger Causalitynumber of lags (no zero) 1ssr based F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1ssr based chi2 test: chi2=55.6014 , p=0.0000 , df=1likelihood ratio test: chi2=49.1426 , p=0.0000 , df=1parameter F test: F=54.7797 , p=0.0000 , df_denom=200, df_num=1Granger Causalitynumber of lags (no zero) 2ssr based F test: F=162.6989, p=0.0000 , df_denom=197, df_num=2ssr based chi2 test: chi2=333.6567, p=0.0000 , df=2likelihood ratio test: chi2=196.9956, p=0.0000 , df=2parameter F test: F=162.6989, p=0.0000 , df_denom=197, df_num=2
22. 下一步是什么?
這就是我們現(xiàn)在要說的。我們從非常基礎(chǔ)的內(nèi)容開始,理解了時間序列不同特征。一旦分析完成之后,接下來的一步是預(yù)測。
原文標(biāo)題:
Time Series Analysis in Python – A Comprehensive Guide with Examples
原文鏈接:
https://www.machinelearningplus.com/time-series/time-series-analysis-python/
編輯:黃繼彥
