最長公共子串(動態(tài)規(guī)劃)

來源：https://www.cnblogs.com/fanguangdexiaoyuer/p/11281179.html

1 描述

有兩個字符串（可能包含空格）,請找出其中最長的公共連續(xù)子串,輸出其長度。(長度在1000以內(nèi))

例如：

輸入：abcde bcd

輸出：3

2 解析

1、把兩個字符串分別以行和列組成一個二維矩陣。

2、比較二維矩陣中每個點對應(yīng)行列字符中否相等，相等的話值設(shè)置為1，否則設(shè)置為0。

3、通過查找出值為1的最長對角線就能找到最長公共子串。

比如：str=acbcbcef，str2=abcbced，則str和str2的最長公共子串為bcbce，最長公共子串長度為5。

針對于上面的兩個字符串我們可以得到的二維矩陣如下：

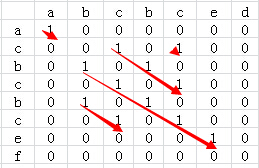
從上圖可以看到，str1和str2共有5個公共子串，但最長的公共子串長度為5。

為了進一步優(yōu)化算法的效率，我們可以再計算某個二維矩陣的值的時候順便計算出來當(dāng)前最長的公共子串的長度，即某個二維矩陣元素的值由record[i][j]=1演變?yōu)閞ecord[i][j]=1 +record[i-1][j-1]，這樣就避免了后續(xù)查找對角線長度的操作了。修改后的二維矩陣如下：

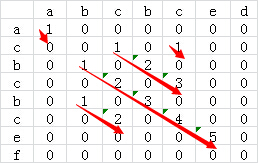
遞推公式為：

當(dāng)A[i] != B[j]，dp[i][j] = 0

當(dāng)A[i] == B[j]，

若i = 0 || j == 0，dp[i][j] = 1

否則 dp[i][j] = dp[i - 1][j - 1] + 1

3 代碼

暴力法

public?int?getLCS(String?s,?String?s2)?
{
????????if?(s?==?null?||?t?==?null)?
????????{
????????????return?0;
????????}
????????int?l1?=?s.length();
????????int?l2?=?t.length();
????????int?res?=?0;
????????for?(int?i?=?0;?i?????????{
????????????for?(int?j?=?0;?j?????????????{
????????????????int?m?=?i;
????????????????int?k?=?j;
????????????????int?len?=?0;
????????????????while?(m?????????????????????len++;
????????????????????m++;
????????????????????k++;
????????????????}
????????????????res?=?Math.max(res,?len);
????????????}
????????}
????????return?res;
}

動態(tài)規(guī)劃

public?int?getLCS(String?s,?String?t)?
{
????????if?(s?==?null?||?t?==?null)?
????????{
????????????return?0;
????????}
????????int?result?=?0;
????????int?sLength?=?s.length();
????????int?tLength?=?t.length();
????????int[][]?dp?=?new?int[sLength][tLength];
????????for?(int?i?=?0;?i?????????????for?(int?k?=?0;?k?????????????????if?(s.charAt(i)?==?t.charAt(k))?{
????????????????????if?(i?==?0?||?k?==?0)?{
????????????????????????dp[i][k]?=?1;
????????????????????}?else?{
????????????????????????dp[i][k]?=?dp[i?-?1][k?-?1]?+?1;
????????????????????}
????????????????????result?=?Math.max(dp[i][k],?result);
????????????????}?else?{
????????????????????dp[i][k]?=?0;
????????????????}
????????????}
????????}
????????return?result;
}

簡化一下遞推公式：

當(dāng)A[i] != B[j]，dp[i][j] = 0

否則 dp[i][j] = dp[i - 1][j - 1] + 1

全部都歸結(jié)為一個公式即可，二維數(shù)組默認值為0

public?int?getLCS(String?s,?String?t)?
{
????????if?(s?==?null?||?t?==?null)?
????????{
????????????return?0;
????????}
????????int?result?=?0;
????????int?sLength?=?s.length();
????????int?tLength?=?t.length();
????????int[][]?dp?=?new?int[sLength?+?1][tLength?+?1];
????????for?(int?i?=?1;?i?<=?sLength;?i++)?{
????????????for?(int?k?=?1;?k?<=?tLength;?k++)?{
????????????????if?(s.charAt(i?-?1)?==?t.charAt(k?-?1))?{
????????????????????dp[i][k]?=?dp[i?-?1][k?-?1]?+?1;
????????????????????result?=?Math.max(dp[i][k],?result);
????????????????}
????????????}
????????}
????????return?result;
}