【機器學習基礎(chǔ)】邏輯回歸優(yōu)化技巧總結(jié)（全）
邏輯回歸由于其簡單高效、易于解釋，是工業(yè)應(yīng)用最為廣泛的模型之一，比如用于金融風控領(lǐng)域的評分卡、互聯(lián)網(wǎng)的推薦系統(tǒng)。?
本文從實際應(yīng)用出發(fā)，以數(shù)據(jù)特征、優(yōu)化算法、模型優(yōu)化等方面，全面地歸納了邏輯回歸（LR）優(yōu)化技巧。
一、LR的特征生成
邏輯回歸是簡單的廣義線性模型，模型的擬合能力很有限，無法學習到特征間交互的非線性信息：一個經(jīng)典的示例是LR無法正確分類非線性的XOR數(shù)據(jù)，而通過引入非線性的特征（特征生成），可在更高維特征空間實現(xiàn)XOR線性可分，如下示例代碼：
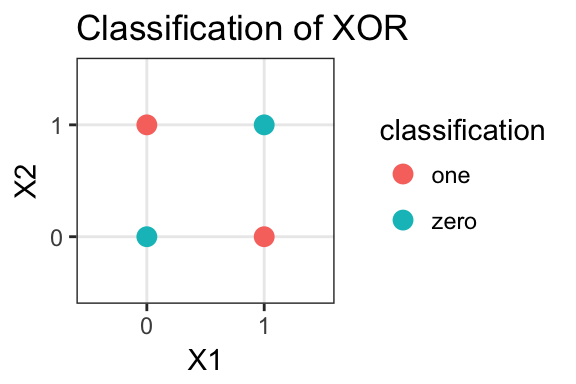
#?生成xor數(shù)據(jù)
import?pandas?as?pd?
xor_dataset?=?pd.DataFrame([[1,1,0],[1,0,1],[0,1,1],[0,0,0]],columns=['x0','x1','label'])
x,y?=?xor_dataset[['x0','x1']],?xor_dataset['label']
xor_dataset.head()
#?keras實現(xiàn)邏輯回歸
from?keras.layers?import?*
from?keras.models?import?Sequential,?Model
from?tensorflow?import?random
np.random.seed(5)?#?固定隨機種子
random.set_seed(5)
model?=?Sequential()
model.add(Dense(1,?input_dim=3,?activation='sigmoid'))
model.summary()
model.compile(optimizer='adam',?loss='binary_crossentropy')
xor_dataset['x2']?=?xor_dataset['x0']?*?xor_dataset['x1']?#?加入非線性特征
x,y?=?xor_dataset[['x0','x1','x2']],?xor_dataset['label']
model.fit(x,?y,?epochs=10000,verbose=False)
print("正確標簽：",y.values)
print("模型預測：",model.predict(x).round())
#?正確標簽：?[0 1 1 0]???模型預測：?[0 1 1 0]
業(yè)界常說“數(shù)據(jù)和特征決定了機器學習的上限，而模型和算法只是逼近這個上限而已”。由于LR是簡單模型，其特征質(zhì)量基本決定了其最終效果（也就是簡單模型要比較折騰特征工程）。
LR常用特征生成（提取）的方式主要有3種：
人工結(jié)合業(yè)務(wù)衍生特征：人工特征的好處是加工出的特征比較有業(yè)務(wù)解釋性，更貼近實際業(yè)務(wù)。缺點是很依賴業(yè)務(wù)知識，耗時。
特征衍生工具：如通過featuretools暴力衍生特征 ，ft生成特征的常用方法有聚合(求平均值、最大值最小值)、轉(zhuǎn)換(特征間加減乘除)的方式。暴力衍生特征速度較快。缺點是更占用計算資源，容易產(chǎn)生一些噪音，而且不太適合要求特征解釋性的場景。（需要注意的：簡單地加減做線性加工特征的方法對于LR是沒必要的，模型可以自己表達）
基于模型的方法：
如POLY2、引入隱向量的因子分解機(FM）可以看做是LR的基礎(chǔ)上，對所有特征進行了兩兩交叉，生成非線性的特征組合。
但FM等方法只能夠做二階的特征交叉，更為有效的是，利用GBDT自動進行篩選特征并生成特征組合。也就是提取GBDT子樹的特征劃分及組合路徑作為新的特征，再把該特征向量當作LR模型輸入，也就是推薦系統(tǒng)經(jīng)典的GBDT +LR方法。(需要注意的，GBDT子樹深度太深的化，特征組合層次比較高，極大提高LR模型擬合能力的同時，也容易引入一些噪聲，導致模型過擬合)
如下GBDT+LR的代碼實現(xiàn)(基于癌細胞數(shù)據(jù)集)，提取GBDT特征，并與原特征拼接：
訓練并評估模型有著較優(yōu)的分類效果：
##?GBDT?+LR?，公眾號閱讀原文，可訪問Github源碼
from?sklearn.preprocessing?import?OneHotEncoder
from?sklearn.ensemble?import?GradientBoostingClassifier
gbdt?=?GradientBoostingClassifier(n_estimators=50,?random_state=10,?subsample=0.8,?max_depth=6,
??????????????????????????????????min_samples_split=20)
gbdt.fit(x_train,?y_train)?#?GBDT?訓練集訓練
train_new_feature?=?gbdt.apply(x)?#?返回數(shù)據(jù)在訓練好的模型里每棵樹中所處的葉子節(jié)點的位置
print(train_new_feature.shape)
train_new_feature?=?train_new_feature.reshape(-1,?50)
display(train_new_feature)
print(train_new_feature.shape)
enc?=?OneHotEncoder()
enc.fit(train_new_feature)
train_new_feature2?=?np.array(enc.transform(train_new_feature).toarray())??#?onehot表示
print(train_new_feature2.shape)
train_new_feature2
二、特征離散化及編碼表示
LR對于連續(xù)性的數(shù)值特征的輸入，通常需要對特征做下max-min歸一化（x =x-min/(max-min)，轉(zhuǎn)換輸出為在 0-1之間的數(shù)，這樣可以加速模型計算及訓練收斂。但其實在工業(yè)界，很少直接將連續(xù)值作為邏輯回歸模型的特征輸入，而是先將連續(xù)特征離散化（常用的有等寬、等頻、卡方分箱、決策樹分箱等方式，而分箱的差異也直接影響著模型效果），然后做（Onehot、WOE）編碼再輸入模型。
之所以這樣做，我們回到模型的原理，邏輯回歸是廣義線性模型，模型無非就是對特征線性的加權(quán)求和，在通過sigmoid歸一化為概率。這樣的特征表達是很有限的。以年齡這個特征在識別是否存款為例。在lr中，年齡作為一個特征對應(yīng)一個權(quán)重w控制，輸出值 = sigmoid(...+age * w+..)，可見年齡數(shù)值大小在模型參數(shù)w的作用下只能呈線性表達。
但是對于年齡這個特征來說，不同的年齡值，對模型預測是否會存款，應(yīng)該不是線性關(guān)系，比如0-18歲可能對于存款是負相關(guān)，19-55對于存款可能就正相關(guān)。這意味著不同的特征值，需要不同模型參數(shù)來更好地表達。也就是通過對特征進行離散化，比如年齡可以離散化以及啞編碼（onehot）轉(zhuǎn)換成4個特征（if_age<18, if_18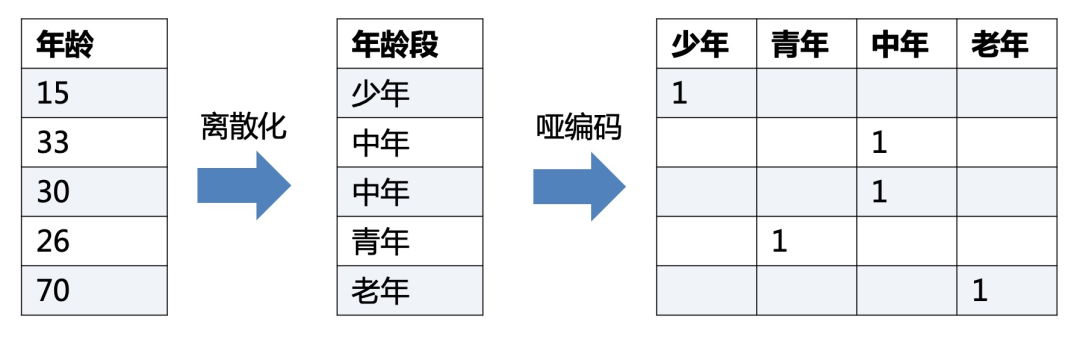
在風控領(lǐng)域，特征離散后更常用特征表示（編碼）還不是onehot，而是WOE編碼。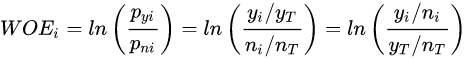
woe編碼是通過對當前分箱中正負樣本的比值Pyi與所有樣本中正負樣本比值Pni的差異（如上式），計算出各個分箱的woe值，作為該分箱的數(shù)值表示。
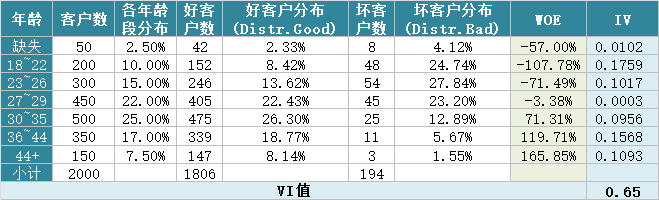
經(jīng)過分箱、woe編碼后的特征很像是決策樹的決策過程，以年齡特征為例：if age >18 and age<22 ?then ?return - 0.57（年齡數(shù)值轉(zhuǎn)為對應(yīng)WOE值）; if age >44 ?then ?return 1.66；...;將這樣的分箱及編碼（對應(yīng)樹的特征劃分、葉子節(jié)點值）輸入LR，很類似于決策樹與LR的模型融合，而提高了模型的非線性表達。
總結(jié)下離散化編碼的優(yōu)點：
邏輯回歸的擬合能力有限，當變量離散化為N個后，每個變量有單獨的權(quán)重，相當于為模型引入了非線性，能夠提升模型擬合能力的同時，也有更好的解釋性。而且離散化后可以方便地進行特征交叉，由M+N個變量變?yōu)镸*N個變量，可以進一步提升表達能力。 離散化后的特征對異常數(shù)據(jù)有較強的魯棒性：比如一個特征是年齡>44是1，否則0。如果特征沒有離散化，一個異常數(shù)據(jù)“年齡200歲”輸入會給模型造成很大的干擾，而將其離散后歸到相應(yīng)的分箱影響就有限。 離散化后模型會更穩(wěn)定，且不容易受到噪聲影響，減少過擬合風險：比如對用戶年齡離散化，18-22作為一個區(qū)間，不會因為一個用戶年齡長了一歲就變成一個完全不同樣本。
三、特征選擇
特征選擇用于篩選出顯著特征、摒棄非顯著特征。可以降低運算開銷，減少干擾噪聲，降低過擬合風險，提升模型效果。對于邏輯回歸常用如下三種選擇方法：
過濾法：利用缺失率、單值率、方差、pearson相關(guān)系數(shù)、VIF、IV值、PSI、P值等指標對特征進行篩選；?
嵌入法：使用帶L1正則項的邏輯回歸，有特征選擇（稀疏解）的效果；
包裝法：使用逐步邏輯回歸，雙向搜索選擇特征。
其中，過濾法提到的VIF是共線性指標，其原理是分別嘗試以各個特征作為標簽，用其他特征去學習擬合，得到線性回歸模型擬合效果的R^2值，算出各個特征的VIF。特征的VIF為1，即無法用其他特征擬合出當前特征，特征之間完全沒有共線性（工程上常用VIF<10作為閾值）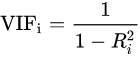
共線性對于廣義線性模型主要影響了特征實際的顯著性及權(quán)重參數(shù)（比如，該特征業(yè)務(wù)上應(yīng)該正相關(guān)，而權(quán)重值卻是負的），也會消弱模型解釋性以及模型訓練的穩(wěn)定性。
四、模型層面的優(yōu)化
4.1 截距項
通過設(shè)置截距項（偏置項）b可以提高邏輯回歸的擬合能力。截距項可以簡單理解為模型多了一個參數(shù)b（也可以看作是新增一列常數(shù)項特征對應(yīng)的參數(shù)w0），這樣的模型復雜度更高，有更好的擬合效果。
如果沒有截距項b呢？我們知道邏輯回歸的決策邊界是線性的（即決策邊界為W * X + b），如果沒有截距項（即W * X），決策邊界就限制在必須是通過坐標圓點的，這樣的限制很有可能導致模型收斂慢、精度差，擬合不好數(shù)據(jù)，即容易欠擬合。
4.2 正則化策略
通過設(shè)定正則項可以減少模型的過擬合風險，常用的正則策略有L1，L2正則化：
L2 參數(shù)正則化 (也稱為嶺回歸、Tikhonov 正則) 通常被稱為權(quán)重衰減 (weight decay)，是通過向?標函數(shù)添加?個正則項 ?(θ) ，使權(quán)重更加接近原點，模型更為簡單。從貝葉斯角度，L2的約束項可以視為模型參數(shù)引入先驗的高斯分布約束（參見《Lazy Sparse Stochastic Gradient Descent for Regularized》 ?）。如下為目標函數(shù)J再加上L2正則式：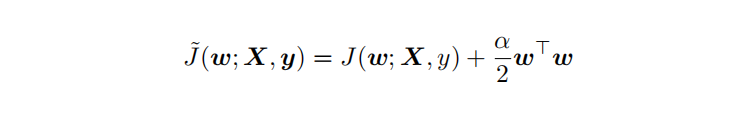 
對帶L2目標函數(shù)的模型參數(shù)更新權(quán)重，?學習率：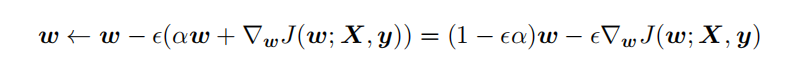
從上式可以看出，加?權(quán)重衰減后會導致學習規(guī)則的修改，即在每步執(zhí)?梯度更新前先收縮權(quán)重 (乘以 1 ? ?α )，有權(quán)重衰減的效果。
L1 正則化（Lasso回歸）是通過向?標函數(shù)添加?個參數(shù)懲罰項 ?(θ)，為各個參數(shù)的絕對值之和。從貝葉斯角度，L1的約束項也可以視為模型參數(shù)引入拉普拉斯分布約束。如下為目標函數(shù)J再加上L1正則式：
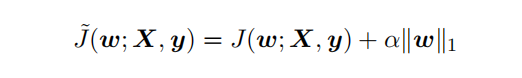
對帶L1目標函數(shù)的模型參數(shù)更新權(quán)重（其中 sgn(x) 為符號函數(shù)，取參數(shù)的正負號）：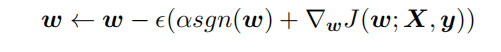
可見，在-αsgn(w)項的作用下， ?w各元素每步更新后的權(quán)重向量都會平穩(wěn)地向0靠攏，w的部分元素容易為0，造成稀疏性。
總結(jié)下L1，L2正則項：
L1，L2都是限制解空間，減少模型容量的方法，以到達減少過擬合的效果。L2范式約束具有產(chǎn)生平滑解的效果，沒有稀疏解的能力，即參數(shù)并不會出現(xiàn)很多零。假設(shè)我們的決策結(jié)果與兩個特征有關(guān)，L2正則傾向于綜合兩者的影響，給影響大的特征賦予高的權(quán)重；而L1正則傾向于選擇影響較大的參數(shù)，而盡可能舍棄掉影響較小的那個（有稀疏解效果）。在實際應(yīng)用中 L2正則表現(xiàn)往往會優(yōu)于 L1正則，但 L1正則會壓縮模型，降低計算量。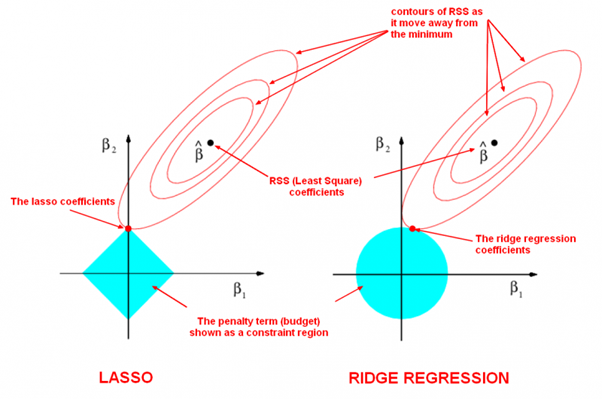
4.3 多分類任務(wù)
當邏輯回歸應(yīng)用于二分類任務(wù)時有兩種主要思路，
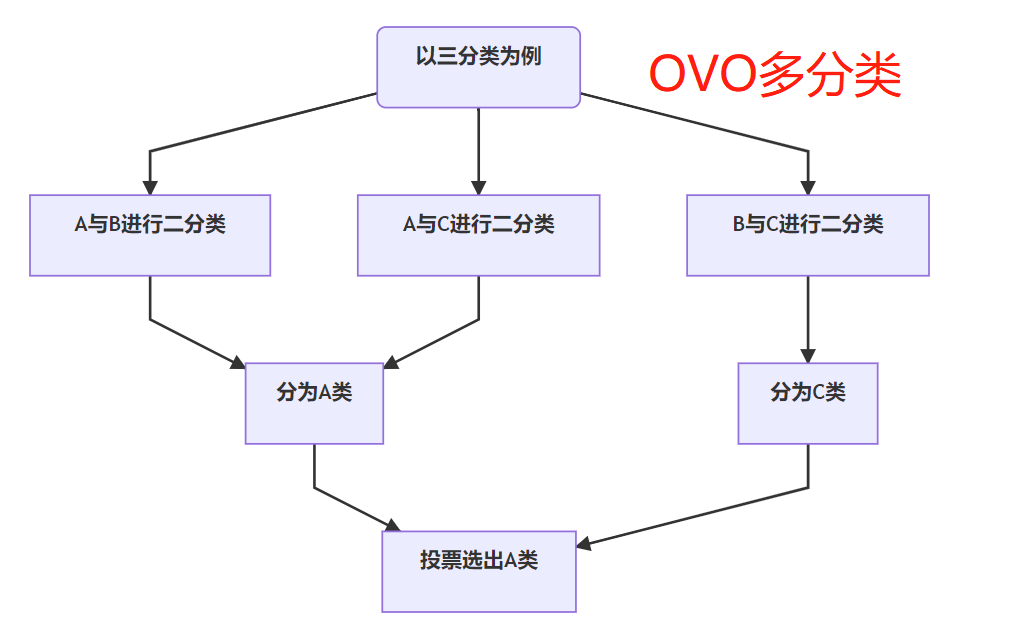
沿用Sigmoid激活函數(shù)的二分類思路，把多分類變成多個二分類組合有兩種實現(xiàn)方式：OVR(one-vs-rest)的思想就是用一個類別去與其他匯總的類別進行二分類, 進行多次這樣的分類, 選擇概率值最大的那個類別；OVO(One vs One)每個分類器只挑兩個類別做二分類, 得出屬于哪一類，最后把所有分類器的結(jié)果放在一起, 選擇最多的那個類別，如下圖：
另外一種，將Sigmoid激活函數(shù)換成softmax函數(shù)，相應(yīng)的模型也可以叫做多元邏輯回歸（Multinomial Logistic Regression），即可適用于多分類的場景。softmax函數(shù)簡單來說就是將多個神經(jīng)元（神經(jīng)元數(shù)目為類別數(shù)）輸出的結(jié)果映射到對于總輸出的占比（范圍0~1，占比可以理解成概率值），我們通過選擇概率最大輸出類別作為預測類別。
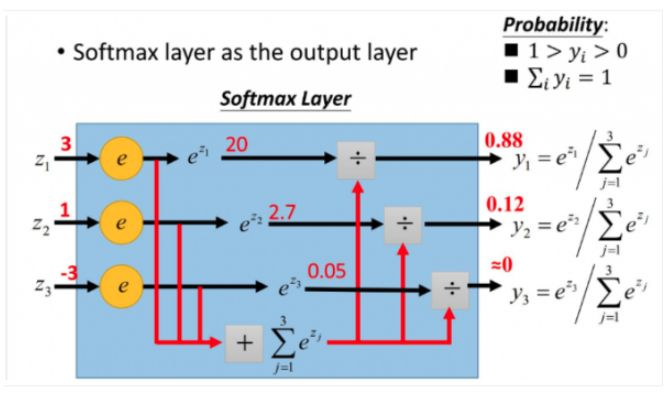如下softmax函數(shù)及對應(yīng)的多分類目標函數(shù)：
softmax回歸中，一般是假設(shè)多個類別是互斥的，樣本在softmax中的概率公式中計算后得到的是樣本屬于各個類別的值，各個類別的概率之和一定為1，而采用logistic回歸OVR進行多分類時，得到的是值是樣本相對于其余類別而言屬于該類別的概率，一個樣本在多個分類器上計算后得到的結(jié)果不一定為1。因而當分類的目標類別是互斥時（例如分辨貓、豬、狗圖片），常采用softmax回歸進行預測，而分類目標類別不是很互斥時（例如分辨流行音樂、搖滾、華語），可以采用邏輯回歸建立多個二分類器（也可考慮下多標簽分類）。
4.4 學習目標
邏輯回歸使用最小化交叉熵損失作為目標函數(shù)，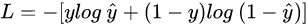
為什么不能用MSE均方誤差？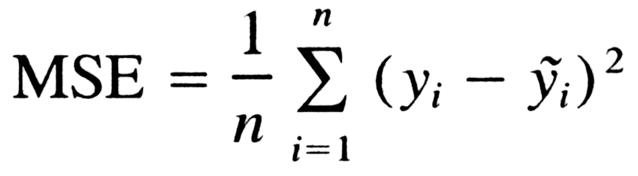
簡單來說，有以下幾點：
MSE 損失函數(shù)的背景假設(shè)是數(shù)據(jù)誤差遵循高斯分布，而二分類問題并不符合這個假設(shè) 。 交叉熵的損失函數(shù)只關(guān)注真實類別對應(yīng)預測誤差的差異。而MSE無差別地關(guān)注全部類別上預測概率和真實類別的誤差，除了增大正確的分類，還會讓錯誤的分類數(shù)值變得平均。 MSE 函數(shù)對于sigmoid二分類問題來說是非凸的，且求導的時候都會有對sigmoid的求導連乘運算，導數(shù)值可能很小而導致收斂變慢，不能保證將損失函數(shù)極小化。但mse也不是完全不能用于分類，對于分類軟標簽就可以考慮MSE。
4.5 優(yōu)化算法
最大似然下的邏輯回歸沒有解析解，我們常用梯度下降之類的算法迭代優(yōu)化得到局部較優(yōu)的參數(shù)解。
如果是Keras等神經(jīng)網(wǎng)絡(luò)庫建模，梯度下降算法類有SGD、Momentum、Adam等優(yōu)化算法可選。對于大多數(shù)任務(wù)而言，通常可以直接先試下Adam，然后可以繼續(xù)在具體任務(wù)上驗證不同優(yōu)化算法效果。
如果用的是scikitl-learn庫建模，優(yōu)化算法主要有l(wèi)iblinear（坐標下降）、newton-cg（擬牛頓法）, lbfgs(擬牛頓法)和sag(隨機平均梯度下降)。liblinear支持L1和L2，只支持OvR做多分類；“l(fā)bfgs”, “sag” “newton-cg”只支持L2，支持OvR和MvM做多分類；當數(shù)據(jù)量特別大，優(yōu)先sag！
4.6 模型評估
4.7 可解釋性
邏輯回歸模型很大的優(yōu)勢就是可解釋性，上節(jié)提到通過離散化編碼（如Onehot）可以提高擬合效果及解釋性，如下特征離散后Onehot編碼：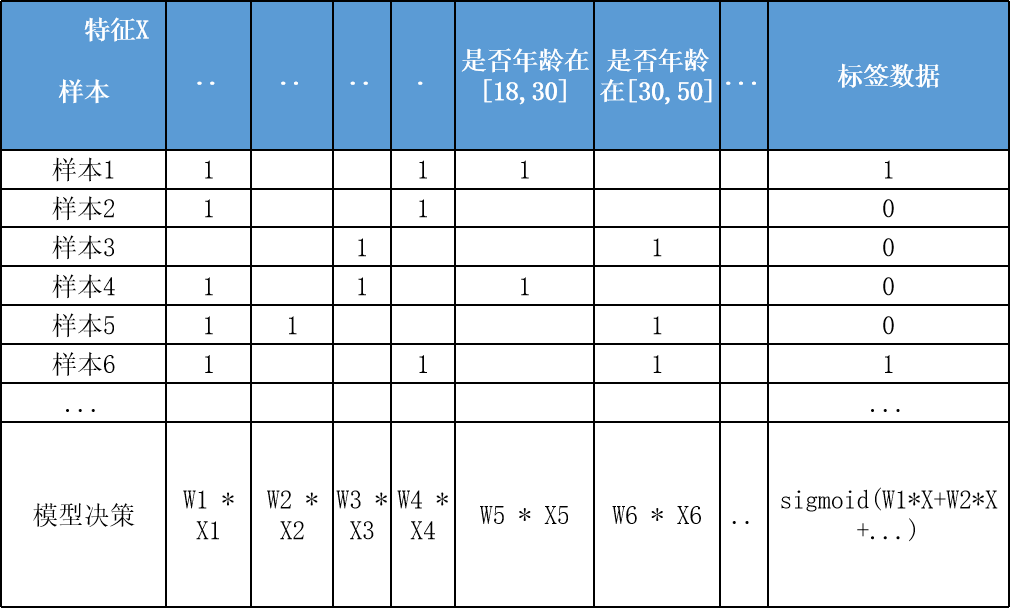
決策過程也就是對特征分箱Xn及其模型權(quán)重Wn的加權(quán)求和，然后sigmoid轉(zhuǎn)為概率，而通過模型權(quán)重值的大小就可以知道各特征對于決策的實際影響程度，比如特征"年齡在[18,30]"對應(yīng)學到權(quán)重值W為-0.8，也就是呈現(xiàn)負相關(guān)。
準備寫本書 屬實逼真，決策樹可視化！ 21個深度學習開源數(shù)據(jù)集匯總！ 耗時一個月，做了一個純粹的機器學習網(wǎng)站 用 Python 從 0 實現(xiàn)一個神經(jīng)網(wǎng)絡(luò) 40篇AI論文！附PDF下載，代碼、視頻講解
三連在看，月入百萬??