【機器學(xué)習(xí)筆記】:邏輯回歸實戰(zhàn)練習(xí)(二)
↑ 關(guān)注 + 星標 ,每天學(xué)Python新技能
后臺回復(fù)【大禮包】送你Python自學(xué)大禮包
作者:xiaoyu
知乎:https://zhuanlan.zhihu.com/pypcfx
介紹:一個半路轉(zhuǎn)行的數(shù)據(jù)挖掘工程師
▍前言
前幾篇介紹了邏輯回歸在機器學(xué)習(xí)中的重要性:5個原因告訴你:為什么在成為數(shù)據(jù)科學(xué)家之前,“邏輯回歸”是第一個需要學(xué)習(xí)的
以及邏輯回歸的理論和公式推導(dǎo):【機器學(xué)習(xí)筆記】:從零開始學(xué)會邏輯回歸(一)
繼上一篇,本篇將引出一個邏輯回歸的實戰(zhàn)練習(xí),利用邏輯回歸進行二分類,通過練習(xí)你將學(xué)會:
理解邏輯回歸模型參數(shù)的含義
使用sklearn構(gòu)建邏輯回歸模型
可視化邏輯回歸分類效果
評估邏輯回歸模型
▍兩個變量的簡單數(shù)據(jù)集
上一篇,我們已經(jīng)推導(dǎo)出了邏輯回歸參數(shù)求解的迭代公式,自己通過numpy和scipy的使用就可以很容易地實現(xiàn)一個邏輯回歸模型。當然,sklearn庫已經(jīng)有了封裝好了的邏輯回歸類LogisticRegression,下面我們將在一個簡單的數(shù)據(jù)集上使用邏輯回歸實現(xiàn)二分類。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from sklearn.linear_model import LogisticRegression
# 導(dǎo)入數(shù)據(jù)集
dataset = pd.read_csv('Social_Network_Ads.csv')
X = dataset.iloc[:, [2, 3]].values
Y = dataset.iloc[:,4].values
# 將數(shù)據(jù)集分成訓(xùn)練集和測試集
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size = 0.2, random_state = 0)
y_test = pd.Series(y_test)
# 簡單的預(yù)處理,特征縮放
from sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
# 構(gòu)建模型,預(yù)測測試集結(jié)果
classifier = LogisticRegression()
classifier.fit(X_train, y_train)
y_pred = classifier.predict(X_test)
通過上面簡單的調(diào)用sklearn庫的類方法我們就訓(xùn)練出了一個簡單的邏輯回歸模型,使用的都是默認參數(shù)。下面讓我們看看簡單的模型分類效果究竟如何。
from matplotlib.colors import ListedColormap
X_set,y_set=X_train,y_train
X1,X2=np.meshgrid(np.arange(start=X_set[:,0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
np.arange(start=X_set[:,1].min()-1, stop=X_set[:,1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('#C65749', '#338DFF')))
plt.xlim(X1.min(),X1.max())
plt.ylim(X2.min(),X2.max())
for i,j in enumerate(np. unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1],
c = ListedColormap(('red', 'blue'))(i), label=j)
plt. title(' LOGISTIC(Training set)')
plt. xlabel(' Age')
plt. ylabel(' Estimated Salary')
plt. legend()
plt. show()
X_set,y_set=X_test,y_test
X1,X2=np. meshgrid(np. arange(start=X_set[:,0].min()-1, stop=X_set[:, 0].max()+1, step=0.01),
np. arange(start=X_set[:,1].min()-1, stop=X_set[:,1].max()+1, step=0.01))
plt.contourf(X1, X2, classifier.predict(np.array([X1.ravel(),X2.ravel()]).T).reshape(X1.shape),
alpha = 0.75, cmap = ListedColormap(('#C65749', '#338DFF')))
plt.xlim(X1.min(),X1.max())
plt.ylim(X2.min(),X2.max())
for i,j in enumerate(np. unique(y_set)):
plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1],
c = ListedColormap(('red', 'blue'))(i), label=j)
plt.title(' LOGISTIC(Test set)')
plt.xlabel(' Age')
plt.ylabel(' Estimated Salary')
plt.legend()
plt.show()
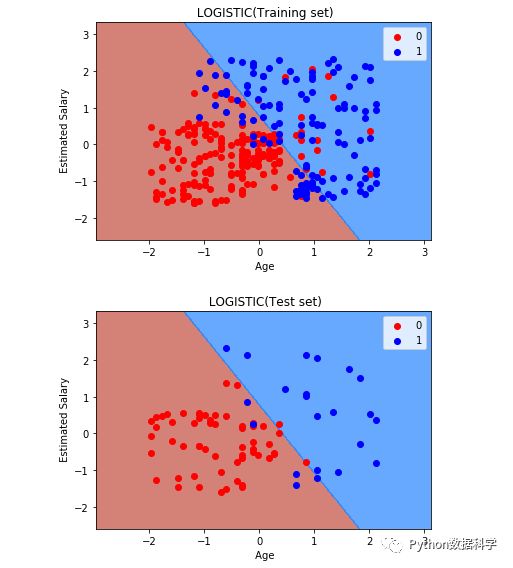
上圖是訓(xùn)練集分類效果,下圖是測試集的分類效果,簡單總結(jié)一下上面內(nèi)容:
Python語言方面:使用了meshgrid方法將二維坐標劃分成了間隔非常小的矩陣細小點,然后使用了contourf方法與模型預(yù)測結(jié)果對比判斷分類結(jié)果。此外,使用了scatter散點圖繪制了原數(shù)據(jù)分布點作為分類前后的比對。
邏輯回歸理論方面:可以明顯看到,在二維坐標中,邏輯回歸是以一條直線進行分類的,很好的說明了邏輯回歸的本質(zhì)是線性分類的。同時我們也看到,目前情況下訓(xùn)練集中混在藍色點中的一些紅色點是無論如何也無法正確的分類出來的,這也正是它的缺點,所以說邏輯回歸的分類準確度還是相對稍低的。
▍更多變量的數(shù)據(jù)集
下面我們將要在一個數(shù)據(jù)量更大,變量更多的的數(shù)據(jù)集上進行測試。由于我們需要一個二分類的數(shù)據(jù)集,所以這里使用了“泰坦尼號生還者預(yù)測”的數(shù)據(jù)集。
https://www.kaggle.com/c/titanic/data
當然,直接使用原始數(shù)據(jù)是不行的。為了方便,數(shù)據(jù)已被我提前處理,經(jīng)過了清洗、預(yù)處理、變換、篩選和衍生,可直接供模型訓(xùn)練。因此,我們可以直接通過sklearn構(gòu)建模型,看一下sklearn中邏輯回歸的參數(shù)都有哪些。
from sklearn.linear_model import LogisticRegression
classifier_default = LogisticRegression()
classifier_default
結(jié)果如下:
LogisticRegression(C=1.0,
class_weight=None,
dual=False,
fit_intercept=True,
intercept_scaling=1,
max_iter=100,
multi_class='ovr',
n_jobs=1,
penalty='l2',
random_state=None,
solver='liblinear',
tol=0.0001,
verbose=0,
warm_start=False)上面是是邏輯回歸的所有參數(shù)配置,都是默認的。乍一看是有很多參數(shù),但其實只有幾個是比較關(guān)鍵的。下面將對邏輯回歸參數(shù)進行總結(jié)分類和解釋。
▍Logistic模型參數(shù)解釋
正則化參數(shù):屬于該分類的參數(shù)有 C 和 penalty。
C:C參數(shù)與懲罰系數(shù)成反比,C值越小,則正則化效果越強,即對參數(shù)的懲罰程度越大。
penalty:提供我們正則化的類型,L1范數(shù)正則化和L2范數(shù)正則化(在線性回歸中相當于lasso回歸和嶺回歸),默認情況下使用L2正則化,但此參數(shù)也需要與solver類型配合使用,因為一些solver有一些限制。關(guān)于L1和L2正則化的區(qū)別和理解后續(xù)進行介紹。
優(yōu)化算法參數(shù)選擇 solver:優(yōu)化算法有四種實現(xiàn)方式,分別是:liblinear,lbfgs,newton-cg,sag,下面是四種算法的介紹。

這四種算法各有一些特點,如果是L2正則化,可選的優(yōu)化算法有newton-cg,lbfgs,liblinear,sag,四個均可以選擇。但是如果是L1正則化,就只能選擇liblinear。這是因為L1正則化的損失函數(shù)不是連續(xù)可導(dǎo)的,而newton-cg,lbfgs,sag這三種優(yōu)化算法都需要損失函數(shù)的一階或者二階連續(xù)導(dǎo)數(shù),liblinear并沒有這個依賴。簡單來說,liblinear對于L1和L2都適用,而其他三種只適用L2。
另外,sag是我們上一篇使用的梯度下降的變種隨機平均梯度下降,它每次僅使用了部分樣本進行梯度迭代,所以當數(shù)據(jù)量較少時不宜選用,而當數(shù)據(jù)量很大時,sag是第一選擇,計算速度會加快。但是sag不能用于L1正則化,所以當你有大量的樣本,又需要L1正則化的話就要自己做取舍了。要么通過對樣本采樣來降低樣本量,要么回到L2正則化。
迭代參數(shù):相關(guān)參數(shù)有max_iter和tol。
max_iter:參數(shù)求解的迭代次數(shù),默認100。迭代次數(shù)過小會影響準確率,迭代次數(shù)過高會影響速度,一般會折中考慮。
tol:殘差收斂條件,即迭代的連續(xù)兩次之間殘差小于tol就停止,默認是0.0001。
權(quán)重參數(shù) class_weight:這個參數(shù)可以調(diào)節(jié)樣本比例。一個很常見的例子是網(wǎng)貸違約預(yù)測中用戶的好壞比,通常好用戶占絕大部分,所以樣本是不均衡的。除了采樣方法處理外,也可以使用該參數(shù)進行調(diào)節(jié)。參數(shù)選擇 balanced 則可以自動計算樣本比例來達到平衡,或者也可以通過自定義比例來達到同樣效果。
多分類參數(shù) multi_class:我們上面舉的例子都是默認二分類的,但邏輯回歸也可以用于多分類,有 ovr 和 multinomial 兩個值可以選擇,默認是 ovr。ovr是one-vs-rest(OvR),而multinomial是many-vs-many(MvM)。如果是二元邏輯回歸,ovr和multinomial并沒有任何區(qū)別,區(qū)別主要在多元邏輯回歸上。
OvR相對簡單,但分類效果相對略差(這里指大多數(shù)樣本分布情況,某些樣本分布下OvR可能更好)。而MvM分類相對精確,但是分類速度沒有OvR快。如果選擇了ovr,則4種損失函數(shù)的優(yōu)化方法liblinear,newton-cg, lbfgs和sag都可以選擇。但是如果選擇了multinomial,則只能選擇newton-cg, lbfgs和sag了。
了解參數(shù)的意義后,我們可以開始嘗試調(diào)節(jié)一下這些參數(shù),通過參數(shù)調(diào)節(jié),可以有效避免過擬合等現(xiàn)象,以此實現(xiàn)一個效果更優(yōu),更健壯的模型。
▍Logistic模型參數(shù)調(diào)試
下面我們手動調(diào)節(jié)幾個參數(shù),來感受一下這些參數(shù)是如何影響最終結(jié)果的。
# 配置調(diào)節(jié)參數(shù)
C_list = [0.0001, 1, 1000]
max_iter_list = [1, 50, 100]
classifiers = ClassifierGenerator('C', C_list)
Auc_plot(classifiers, X_test, 'C')
當然,對于不同參數(shù)的選擇,我們可以通過查看ROC和AUC,以此來衡量結(jié)果。首先,我們調(diào)節(jié)C參數(shù),分別是0.0001,1,和1000,查看這三個不同值下的ROC曲線和AUC值。如果對ROC/AUC不清楚,可以參考:【機器學(xué)習(xí)筆記】:一文讓你徹底記住什么是ROC/AUC(看不懂你來找我)
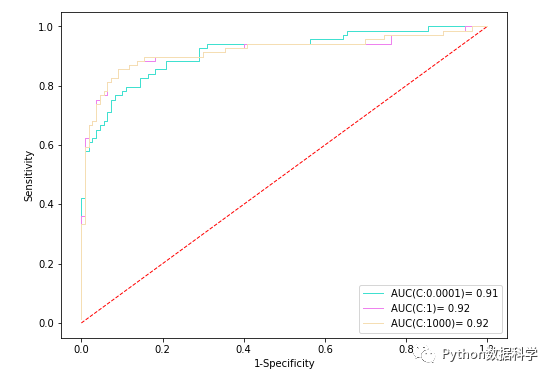
上面是三個C取值在測試集數(shù)據(jù)上的評估結(jié)果,可以看到:C=0.0001的時候,AUC值為0.91,這說明模型可能出現(xiàn)了過擬合的現(xiàn)象。因為,C越小,懲罰程度越大,參數(shù)可能過度學(xué)習(xí)而無法在測試集上泛化,因此測試集上AUC值相對低。
而C的其它兩個取值,1和1000,雖然二者ROC曲線稍有不同,但是AUC值都是0.92,所以就單獨C參數(shù)來講,二者皆可。
同樣的,可以對比不同max_iter參數(shù)值的不同結(jié)果。
# 配置調(diào)節(jié)參數(shù)
C_list = [0.0001, 1, 1000]
max_iter_list = [1, 100]
classifiers = ClassifierGenerator('max_iter', max_iter_list)
Auc_plot(classifiers, X_test, 'max_iter')
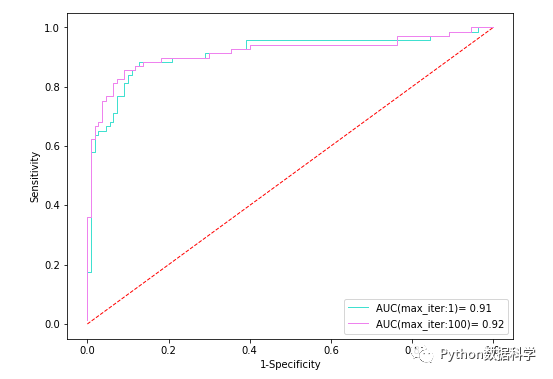
迭代次數(shù)為1情況下AUC值0.91,偏低,而為100的時候AUC值為0.92。這說明迭代次數(shù)(max_iter=1)太低導(dǎo)致出現(xiàn)了欠擬合。
▍自動化查找最優(yōu)參數(shù)
上面我們手動地調(diào)節(jié)了一些參數(shù),但是這些參數(shù)是一起其作用的,單獨調(diào)節(jié)的情況下不一定能夠保證最好,最好的情況是一個完美的參數(shù)搭配或者組合。那么如何找到這樣的搭配呢?除了憑借經(jīng)驗手動調(diào)參以外,還可以使用sklearn的一個工具。
sklearn中提供了一種自動搜索最優(yōu)參數(shù)的方法:GridSearchCV,它是基于提供的參數(shù)選項,組合出各種可能,然后結(jié)合交叉驗證對所有可能組合進行篩選。因此,通過使用該方法,我們就可以簡單地找到相對上面單獨參數(shù)調(diào)節(jié)更好的參數(shù)組合了。
還是通過上面的例子繼續(xù)說明,自動調(diào)參代碼如下:
from sklearn.model_selection import GridSearchCV
import warnings
warnings.filterwarnings("ignore")
# 參數(shù)設(shè)置
params = {'C':[0.0001, 1, 100, 1000],
'max_iter':[1, 10, 100, 500],
'class_weight':['balanced', None],
'solver':['liblinear','sag','lbfgs','newton-cg']
}
lr = LogisticRegression()
clf = GridSearchCV(lr, param_grid=params, cv=10)
clf.fit(X_train,y_train)將所有參數(shù)設(shè)置考慮進去,訓(xùn)練數(shù)據(jù),結(jié)果我們可以得到:
>>clf.best_params_
out:
{'C': 1, 'class_weight': None, 'max_iter': 10, 'solver': 'sag'}
上面結(jié)果就是我們基于自己提供的參數(shù)選擇要找的最佳參數(shù)組合了。
▍構(gòu)建最優(yōu)模型
有了最優(yōu)的參數(shù)后,我們將這些參數(shù)作為輸入重新建立一個邏輯回歸模型。代碼如下:
# 根據(jù)以上繪圖結(jié)果選擇一個合理參數(shù)值
classifier = LogisticRegression(**clf.best_params_)
# 訓(xùn)練模型
classifier.fit(X_train, y_train)
# 預(yù)測測試集結(jié)果
y_pred = classifier.predict(X_test)
y_score = classifier.predict_proba(X_test)[:,1]
成功構(gòu)建模型后,我們再次進行分類,并看一下最終的評估指標ROC曲線,AUC值,以及KS值:
# roc/auc計算
y_score = classifier.predict_proba(X_test)[:,1]
fpr,tpr,threshold = metrics.roc_curve(y_test, y_score)
roc_auc = metrics.auc(fpr,tpr)
# 繪制roc曲線
f,ax = plt.subplots(figsize=(8,6))
plt.stackplot(fpr, tpr, color='#338DFF', alpha = 0.5, edgecolor = 'black')
plt.plot(fpr, tpr, color='black', lw = 1.5)
plt.plot([0,1],[0,1], color = 'red', linestyle = '--', lw = 2)
plt.text(0.5,0.3,'ROC curve (area = %0.2f)' % roc_auc)
plt.xlabel('1-Specificity')
plt.ylabel('Sensitivity')
plt.show()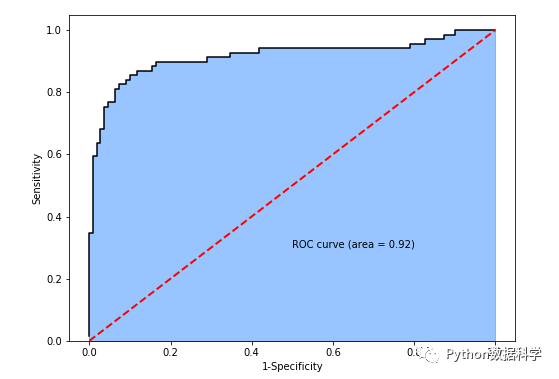
from ks_visual import plot_ks
# 觀察ks指標,并繪制ks曲線
plot_ks(y_test = y_test, y_score = y_score, pf = 1)
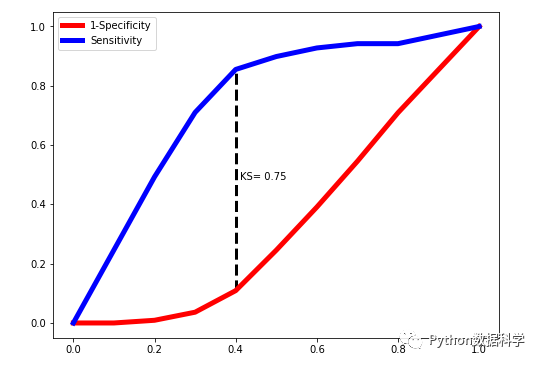
可以看到,AUC值為0.92,KS值為0.75,說明分類模型的區(qū)分能力和準確度都不錯。但要提醒的是:這樣的好結(jié)果并不全是邏輯回歸模型的功勞,而更多的是前期特征工程的貢獻。只有做出好的特征,提高數(shù)據(jù)質(zhì)量,才能最大程度上的提高最終效果。
參考:
https://www.cnblogs.com/pinard/p/6035872.html
從零開始學(xué)習(xí)數(shù)據(jù)分析和挖掘,劉順祥
https://github.com/MLEveryday/100-Days-Of-ML-Code
- END -
推薦閱讀
推薦一個公眾號,幫助程序員自學(xué)與成長
覺得還不錯就給我一個小小的鼓勵吧!


