最炫酷的損失函數(shù)

最近，我看到一篇由Jon Barron在CVPR 2019中提出的關(guān)于為機(jī)器學(xué)習(xí)問(wèn)題開(kāi)發(fā)一個(gè)健壯的和自適應(yīng)的損失函數(shù)的文章。這篇文章是對(duì)那篇論文和一些必要概念的回顧，它還將包含一個(gè)簡(jiǎn)單回歸問(wèn)題上的損失函數(shù)的實(shí)現(xiàn)。

關(guān)于異常值和魯棒的損失的問(wèn)題：

考慮機(jī)器學(xué)習(xí)問(wèn)題中最常用的誤差之一：均方誤差(MSE)，它是(y-x)的形式。MSE的一個(gè)關(guān)鍵特征是它對(duì)大誤差的靈敏度比小誤差高。用MSE訓(xùn)練的模型將偏向于減少最大的誤差。例如，誤差為3與與誤差為9同等重要。

我使用Scikit-Learn創(chuàng)建了一個(gè)例子，以演示在有或沒(méi)有異常值影響的情況下，模型的擬合是如何在一個(gè)簡(jiǎn)單數(shù)據(jù)集中變化的。

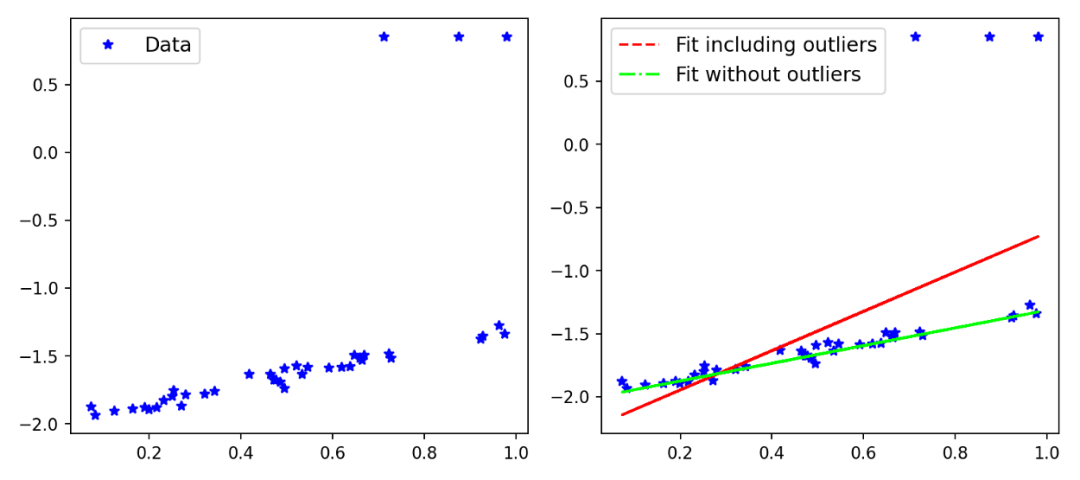
你可以看到的，包含異常值的擬合會(huì)受到異常值的影響，但是優(yōu)化問(wèn)題應(yīng)該要求模型受到inliers的影響要大于離群值。當(dāng)然，在這一點(diǎn)上，你已經(jīng)可以認(rèn)為平均絕對(duì)誤差(MAE)是比MSE更好的選擇，因?yàn)樗鼘?duì)大誤差的敏感性較低。有各種類型的穩(wěn)健性損失(如MAE)，對(duì)于一個(gè)特定的問(wèn)題，我們可能需要測(cè)試各種損失。在訓(xùn)練一個(gè)網(wǎng)絡(luò)的同時(shí)，快速測(cè)試各種損失函數(shù)不是很神奇嗎？本文的主要思想是引入一個(gè)廣義的損失函數(shù)，其中損失函數(shù)的魯棒性可以改變，并可以在訓(xùn)練網(wǎng)絡(luò)的同時(shí)訓(xùn)練這個(gè)超參數(shù)，以提高性能。這比通過(guò)執(zhí)行網(wǎng)格搜索交叉驗(yàn)證來(lái)尋找最佳損失所花費(fèi)的時(shí)間要少得多。讓我們從下面的定義開(kāi)始

魯棒的以及自適應(yīng)的損失：一般形式

魯棒和自適應(yīng)損失的一般形式如下：

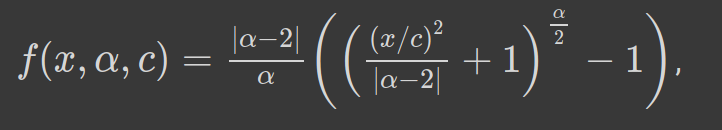
α控制損失函數(shù)的魯棒性。c可以看作是一個(gè)尺度參數(shù)，在x=0附近控制彎曲的尺度。由于α是超參數(shù)，我們可以看到，對(duì)于α的不同值，損失函數(shù)具有相似的形式。讓我們看看下面：

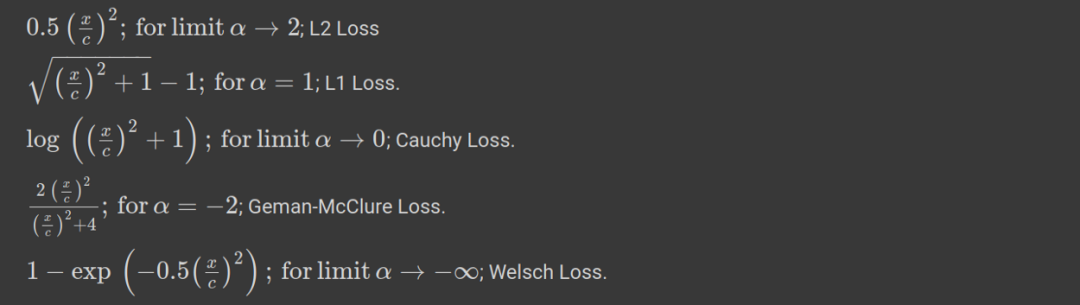
損失函數(shù)在α = 0和2處沒(méi)有定義，但是取極限我們可以進(jìn)行近似。從α =2到α =1，損失平穩(wěn)地從L2損失過(guò)渡到L1損失。對(duì)于不同的值，我們可以繪制損失函數(shù)，看看它如何表現(xiàn)(圖2)。

我們也可以花一些時(shí)間在這個(gè)損失函數(shù)的一階導(dǎo)數(shù)上，因?yàn)榛谔荻鹊膬?yōu)化需要導(dǎo)數(shù)。對(duì)于α的不同值，相對(duì)于x的導(dǎo)數(shù)如下所示。在圖2中，我還繪制了不同α的導(dǎo)數(shù)和損失函數(shù)。

自適應(yīng)損失的表現(xiàn)極其導(dǎo)數(shù)：

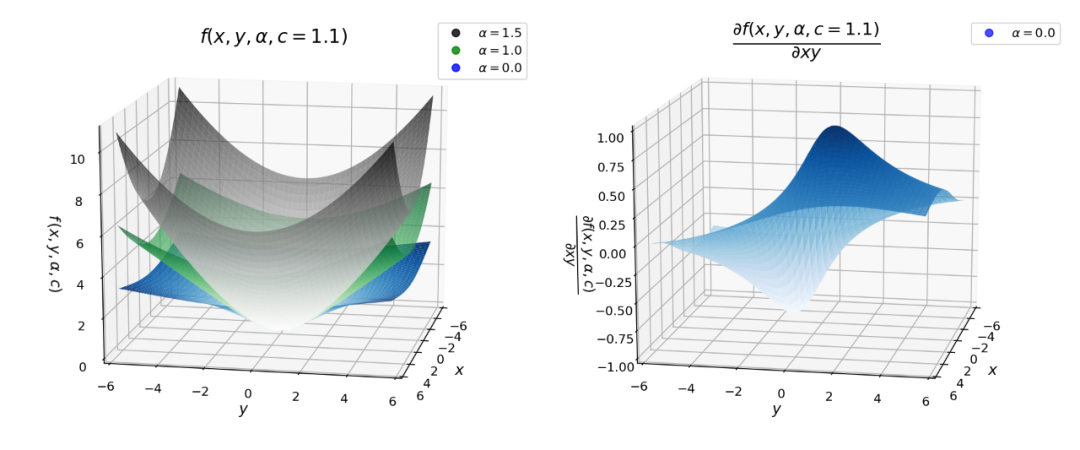
下面的圖對(duì)于理解我們損失的行為是非常重要的。對(duì)于下面的圖，我已經(jīng)將尺度參數(shù)c固定為1.1。當(dāng)x = 6.6時(shí)，我們可以把它當(dāng)做x = 6 × c。根據(jù)下圖，我們可以得出以下關(guān)于損失及其導(dǎo)數(shù)的推論。

1. 損失函數(shù)對(duì)x, α和c>0是平滑的，適用于基于梯度的優(yōu)化。
2. 在原點(diǎn)處損失始終為零，當(dāng)*|x|>0*時(shí)，單調(diào)增加。具有單調(diào)性損失也可以取對(duì)數(shù)損失進(jìn)行比較。
3. 損失相對(duì)于α也是單調(diào)遞增的。這一特性對(duì)于損失函數(shù)的魯棒性非常重要，因?yàn)槲覀兛梢詮囊粋€(gè)較高的α值開(kāi)始，然后在優(yōu)化過(guò)程中逐漸(平穩(wěn)地)減少，從而使魯棒估計(jì)避免局部極小值。
4. 我們看到當(dāng)|x|<c時(shí)，對(duì)于不同的α值，導(dǎo)數(shù)幾乎是線性的。這意味著當(dāng)它們很小的時(shí)候，導(dǎo)數(shù)與殘差的大小成比例。
5. 對(duì)于 α = 2，整個(gè)導(dǎo)數(shù)與殘差的大小成比例。這是一般的MSE (L2)損失的性質(zhì)。
6. 對(duì)于α = 1(L1損失)，我們可以看到，在|x|>c之外，導(dǎo)數(shù)的幅度飽和到一個(gè)恒定值(恰好是1/c)。這意味著殘差的影響永遠(yuǎn)不會(huì)超過(guò)一個(gè)固定的數(shù)值。
7. 對(duì)于 α < 1導(dǎo)數(shù)的大小隨|x|>c的變化而減小。這意味著隨著殘差的增加，它對(duì)梯度的影響較小，因此在梯度下降過(guò)程中，離群點(diǎn)的影響較小。

我還繪制了下面的圖，不同α值的魯棒損失和它的導(dǎo)數(shù)的曲面圖。

魯棒損失的實(shí)現(xiàn)：Pytorch和Google Colab:

既然我們已經(jīng)學(xué)習(xí)了魯棒和自適應(yīng)損失函數(shù)的基本知識(shí)和性質(zhì)，讓我們將其付諸實(shí)踐。下面使用的代碼只是稍微修改了一下Jon Barron 's GitHub存儲(chǔ)庫(kù)中的代碼。我還創(chuàng)建了一個(gè)動(dòng)畫來(lái)描述隨著迭代次數(shù)的增加，自適應(yīng)損失如何找到最佳擬合線。

!pip?install?git+https://github.com/jonbarron/robust_loss_pytorchimport?robust_loss_pytorch?

我們創(chuàng)建一個(gè)簡(jiǎn)單的線性數(shù)據(jù)集，包括正態(tài)分布的噪聲和離群值。因?yàn)閹?kù)使用pytorch，所以我們使用torch將x, y的numpy數(shù)組轉(zhuǎn)換為張量。

import?numpy?as?np
import?torch?

scale_true?=?0.7
shift_true?=?0.15

x?=?np.random.uniform(size=n)
y?=?scale_true?*?x?+?shift_true
y?=?y?+?np.random.normal(scale=0.025,?size=n)?#?add?noise?

flip_mask?=?np.random.uniform(size=n)?>?0.9?
y?=?np.where(flip_mask,?0.05?+?0.4?*?(1.?—?np.sign(y?—?0.5)),?y)?
#?include?outliers

x?=?torch.Tensor(x)
y?=?torch.Tensor(y)

接下來(lái)我們使用pytorch模塊定義一個(gè)線性回歸類，如下所示：

class?RegressionModel(torch.nn.Module):
????
???def?__init__(self):
??????super(RegressionModel,?self).__init__()
??????self.linear?=?torch.nn.Linear(1,?1)?
??????##?applies?the?linear?transformation.
????????
???def?forward(self,?x):
??????return?self.linear(x[:,None])[:,0]?#?returns?the?forward?pass

接下來(lái)，我們對(duì)我們的數(shù)據(jù)擬合一個(gè)線性回歸模型，但首先使用損失函數(shù)的一般形式。在這里，我們使用一個(gè)固定的α值(α = 2.0)，并且它在整個(gè)優(yōu)化過(guò)程中保持不變。正如我們所看到的，對(duì)于α = 2.0，損失函數(shù)等效于L2損失，而這對(duì)于包括異常值在內(nèi)的問(wèn)題來(lái)說(shuō)并不是最優(yōu)的。我們使用學(xué)習(xí)率為0.01的Adam優(yōu)化器。

regression?=?RegressionModel()
params?=?regression.parameters()
optimizer?=?torch.optim.Adam(params,?lr?=?0.01)

for?epoch?in?range(2000):
???y_i?=?regression(x)
???#?Use?general?loss?to?compute?MSE,?fixed?alpha,?fixed?scale.
???loss?=?torch.mean(robust_loss_pytorch.general.lossfun(
?????y_i?—?y,?alpha=torch.Tensor([2.]),?scale=torch.Tensor([0.1])))
???optimizer.zero_grad()
???loss.backward()
???optimizer.step()

利用魯棒損失函數(shù)的一般形式和固定α值，可以得到擬合直線。圖4中繪制了原始數(shù)據(jù)、真實(shí)線(生成數(shù)據(jù)點(diǎn)時(shí)使用的具有相同斜率和偏差的線，排除異常值)和擬合線。

損失函數(shù)的一般形式不允許α改變，因此我們必須手工調(diào)整 α參數(shù)或執(zhí)行網(wǎng)格搜索。此外，如上圖所示，擬合會(huì)受到離群值的影響。這是一般情況但是如果我們使用損失函數(shù)的適應(yīng)性版本會(huì)發(fā)生什么呢？我們調(diào)用adaptive loss模塊，并初始化α，讓它在每個(gè)迭代步驟中自適應(yīng)。

regression?=?RegressionModel()
adaptive?=?robust_loss_pytorch.adaptive.AdaptiveLossFunction(
???????????num_dims?=?1,?float_dtype=np.float32)
params?=?list(regression.parameters())?+?list(adaptive.parameters())
optimizer?=?torch.optim.Adam(params,?lr?=?0.01)
for?epoch?in?range(2000):
???y_i?=?regression(x)
???loss?=?torch.mean(adaptive.lossfun((y_i?—?y)[:,None]))
???#?(y_i?-?y)[:,?None]?#?numpy?array?or?tensor
???optimizer.zero_grad()
???loss.backward()
???optimizer.step()

使用這個(gè)，以及使用Celluloid模塊的一些額外代碼，我創(chuàng)建了下面的動(dòng)畫(圖5)。在這里，你可以清楚地看到，隨著迭代的增加，adaptive loss如何找到最佳擬合線。這個(gè)結(jié)果接近真實(shí)的線，它是可以忽略離群值的影響。

討論:

我們已經(jīng)看到了如何使用包含超參數(shù)α的魯棒損失來(lái)動(dòng)態(tài)地尋找最佳損失函數(shù)。本文還演示了以α為連續(xù)超參數(shù)的損失函數(shù)的魯棒性如何被引入到經(jīng)典的計(jì)算機(jī)視覺(jué)算法中。論文中給出了實(shí)現(xiàn)自適應(yīng)損失的變分自編碼器和單目深度估計(jì)的例子，這些代碼也可以在Jon 's GitHub中找到。但是在這篇論文中，最吸引我的是關(guān)于損失函數(shù)本身的動(dòng)機(jī)和一步一步的推導(dǎo)。