如何選擇合適的損失函數(shù),請看......
點(diǎn)擊上方“小白學(xué)視覺”,選擇加"星標(biāo)"或“置頂”
重磅干貨,第一時(shí)間送達(dá)


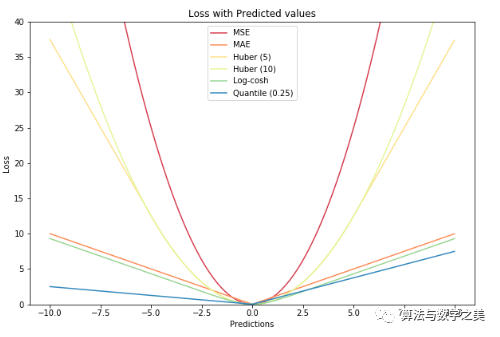
▌回歸損失
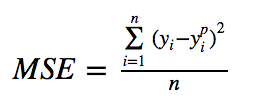 ?
?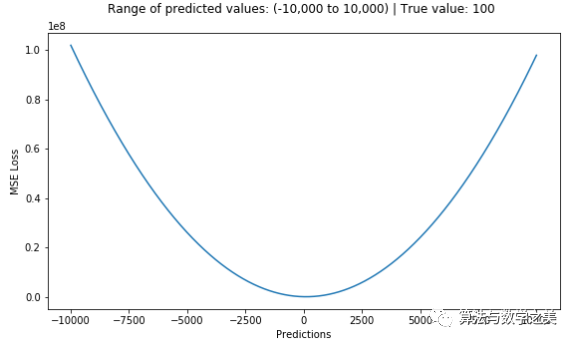 ?
?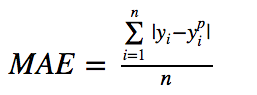 ?
?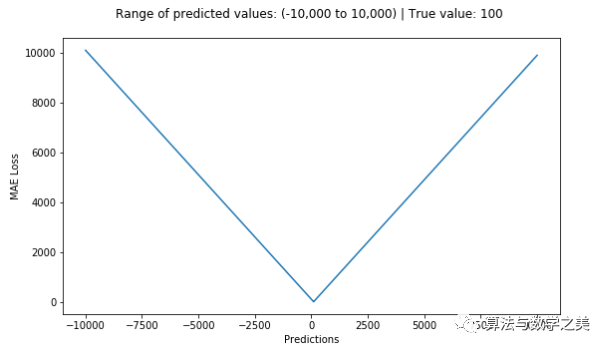 ?
?#true:真正的目標(biāo)變量數(shù)組
#pred:預(yù)測數(shù)組
**
def mse(true, pred):
return np.sum(((true – pred)**2))
**
def mae(true, pred):
return np.sum(np.abs(true – pred))
**
#也可以在sklearn中使用
**
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
 ?
?地址: http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
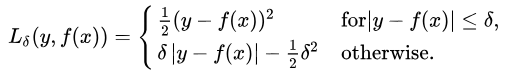 ?
? ?
?
 ?
? ?
?def sm_mae(true, pred, delta):
"""
true: array of true values
pred: array of predicted values
returns: smoothed mean absolute error loss
"""
loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
return np.sum(loss)
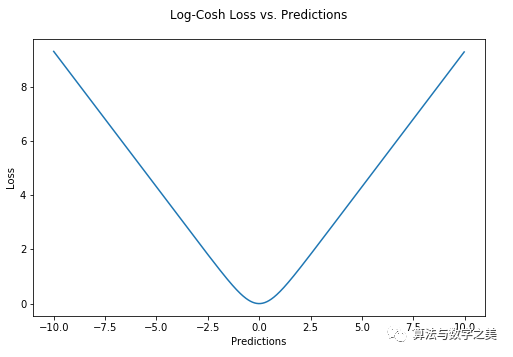
def logcosh(true, pred):
loss = np.log(np.cosh(pred - true))
return np.sum(loss)
 ?
? ?
? ?
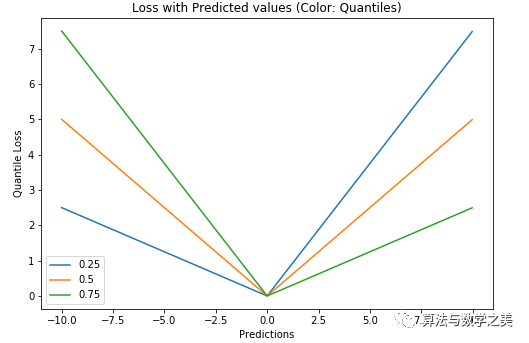
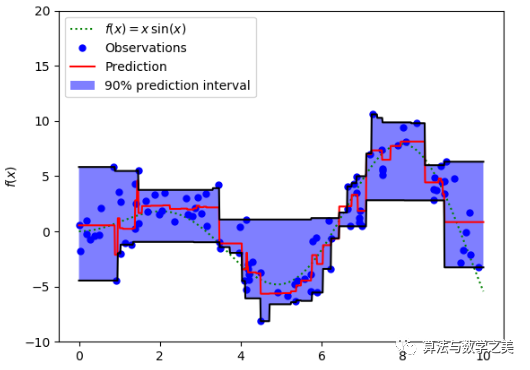
?地址: https://github.com/groverpr/Machine-Learning/blob/master/notebooks/09_Quantile_Regression.ipynb
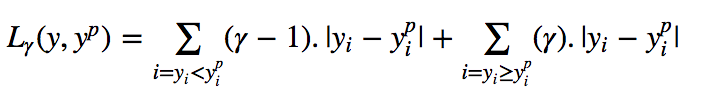 ?
?
 ?
?
▌比較研究
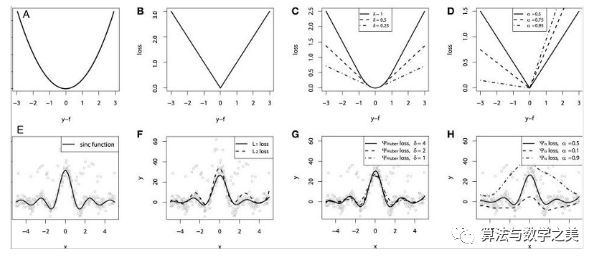 ?
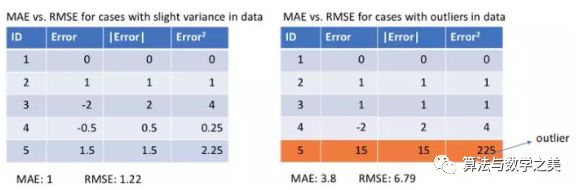
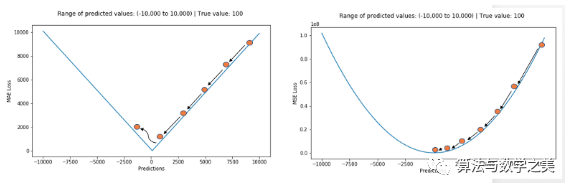
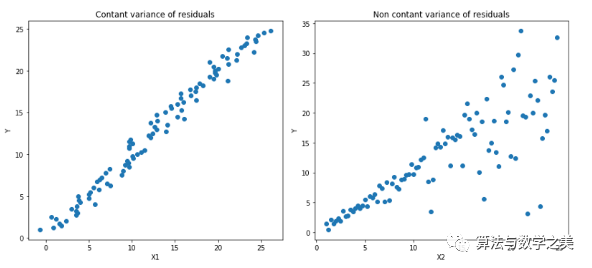
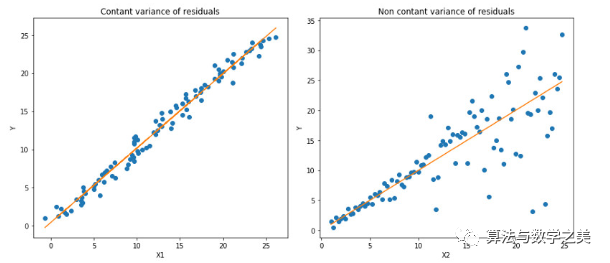
?以MAE為損失的模型預(yù)測較少受到脈沖噪聲的影響,而以MSE為損失的模型的預(yù)測由于脈沖噪聲造成的數(shù)據(jù)偏離而略有偏差。
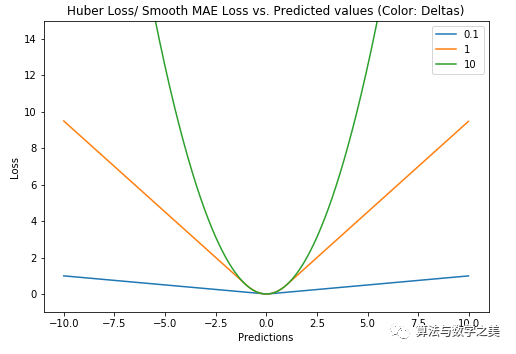
以Huber Loss為損失函數(shù)的模型,其預(yù)測對所選的超參數(shù)不太敏感。
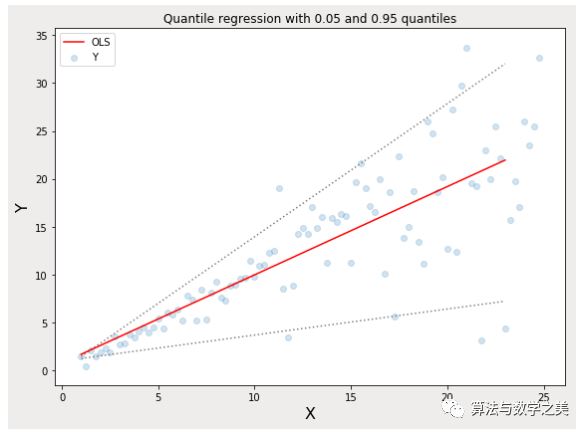
Quantile Loss對相應(yīng)的置信水平給出了很好的估計(jì)。
好消息!
小白學(xué)視覺知識(shí)星球
開始面向外開放啦??????
下載1:OpenCV-Contrib擴(kuò)展模塊中文版教程 在「小白學(xué)視覺」公眾號后臺(tái)回復(fù):擴(kuò)展模塊中文教程,即可下載全網(wǎng)第一份OpenCV擴(kuò)展模塊教程中文版,涵蓋擴(kuò)展模塊安裝、SFM算法、立體視覺、目標(biāo)跟蹤、生物視覺、超分辨率處理等二十多章內(nèi)容。 下載2:Python視覺實(shí)戰(zhàn)項(xiàng)目52講 在「小白學(xué)視覺」公眾號后臺(tái)回復(fù):Python視覺實(shí)戰(zhàn)項(xiàng)目,即可下載包括圖像分割、口罩檢測、車道線檢測、車輛計(jì)數(shù)、添加眼線、車牌識(shí)別、字符識(shí)別、情緒檢測、文本內(nèi)容提取、面部識(shí)別等31個(gè)視覺實(shí)戰(zhàn)項(xiàng)目,助力快速學(xué)校計(jì)算機(jī)視覺。 下載3:OpenCV實(shí)戰(zhàn)項(xiàng)目20講 在「小白學(xué)視覺」公眾號后臺(tái)回復(fù):OpenCV實(shí)戰(zhàn)項(xiàng)目20講,即可下載含有20個(gè)基于OpenCV實(shí)現(xiàn)20個(gè)實(shí)戰(zhàn)項(xiàng)目,實(shí)現(xiàn)OpenCV學(xué)習(xí)進(jìn)階。 交流群
歡迎加入公眾號讀者群一起和同行交流,目前有SLAM、三維視覺、傳感器、自動(dòng)駕駛、計(jì)算攝影、檢測、分割、識(shí)別、醫(yī)學(xué)影像、GAN、算法競賽等微信群(以后會(huì)逐漸細(xì)分),請掃描下面微信號加群,備注:”昵稱+學(xué)校/公司+研究方向“,例如:”張三 + 上海交大 + 視覺SLAM“。請按照格式備注,否則不予通過。添加成功后會(huì)根據(jù)研究方向邀請進(jìn)入相關(guān)微信群。請勿在群內(nèi)發(fā)送廣告,否則會(huì)請出群,謝謝理解~
評論
圖片
表情

