NLP（四十六）常見(jiàn)的損失函數(shù)
??本文將給出NLP任務(wù)中一些常見(jiàn)的損失函數(shù)（Loss Function），并使用Keras、PyTorch給出具體例子。
??在講解具體的損失函數(shù)之前，我們有必要了解下什么是損失函數(shù)。所謂損失函數(shù)，指的是衡量模型預(yù)測(cè)值y與真實(shí)標(biāo)簽Y之間的差距的函數(shù)。本文將介紹的損失函數(shù)如下：
Mean Squared Error（均方差損失函數(shù)）
Mean Absolute Error（絕對(duì)值損失函數(shù)）
Binary Cross Entropy（二元交叉熵?fù)p失函數(shù)）
Categorical Cross Entropy（多分類(lèi)交叉熵?fù)p失函數(shù)）
Sparse Categorical Cross Entropy（稀疏多分類(lèi)交叉熵?fù)p失函數(shù)）
Hingle Loss（合頁(yè)損失函數(shù)）
……
??以下將分別介紹上述損失函數(shù)，并介紹Keras和PyTorch中的例子。在此之前，我們分別導(dǎo)入Keras所需模塊和PyTorch所需模塊。Keras所需模塊如下：
PyTorch所需模塊如下：
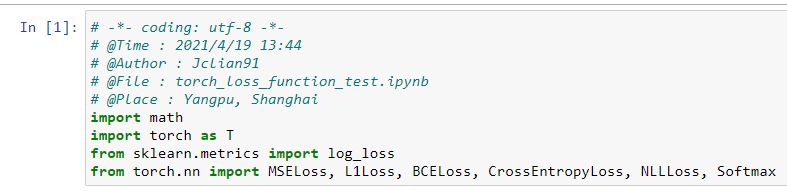
從導(dǎo)入模塊來(lái)看，PyTorch更加簡(jiǎn)潔，在后面的部分中我們將持續(xù)比較這兩種框架的差異。
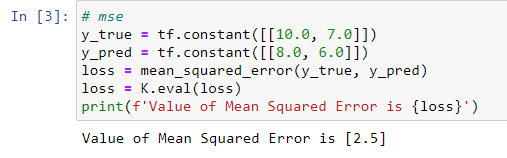
Mean Squared Error
??Mean Squared Error（MSE）為均方差損失函數(shù)，一般用于回歸問(wèn)題。我們用表示樣本預(yù)測(cè)值序列中的第i個(gè)元素，用表示樣本真實(shí)值序列中的第i個(gè)元素，則均方差損失函數(shù)MSE的計(jì)算公式如下：
??Keras實(shí)現(xiàn)代碼如下：
??PyTorch實(shí)現(xiàn)代碼如下：
Mean Absolute Error
??Mean Absolute Error（MAE）為絕對(duì)值損失函數(shù)，一般用于回歸問(wèn)題。我們用表示樣本預(yù)測(cè)值序列中的第i個(gè)元素，用表示樣本真實(shí)值序列中的第i個(gè)元素，則絕對(duì)值損失函數(shù)MAE的計(jì)算公式如下：
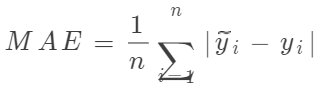
??Keras實(shí)現(xiàn)代碼如下：
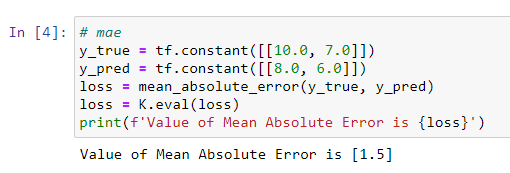
??PyTorch實(shí)現(xiàn)代碼如下：
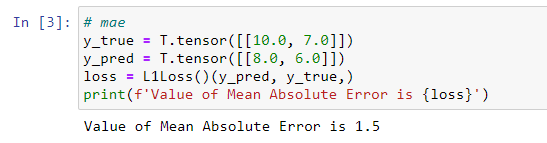
注意，在PyTorch中L1Loss中的L1表示為L(zhǎng)1范數(shù)，即通常所說(shuō)的絕對(duì)值，絕對(duì)值函數(shù)處處連續(xù)，但在x=0處不可導(dǎo)。
Binary Cross Entropy
??Binary Cross Entropy（BCE）為二元交叉熵?fù)p失函數(shù)，一般用于二分類(lèi)問(wèn)題。我們用Y表示樣本真實(shí)標(biāo)簽序列（每個(gè)值為0或者1），用表示樣本預(yù)測(cè)標(biāo)簽序列（每個(gè)值為0-1之間的值），則BCE計(jì)算公式如下：
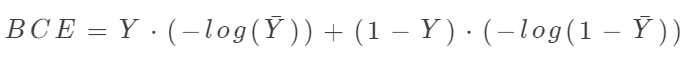
我們不在講解具體的計(jì)算公式，如需具體的計(jì)算方式，可以參考文章Sklearn中二分類(lèi)問(wèn)題的交叉熵計(jì)算。
??Keras實(shí)現(xiàn)代碼如下：
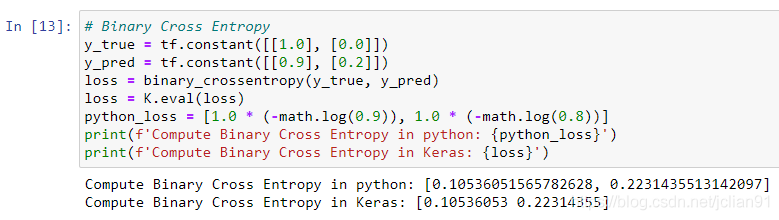
??PyTorch實(shí)現(xiàn)代碼如下：
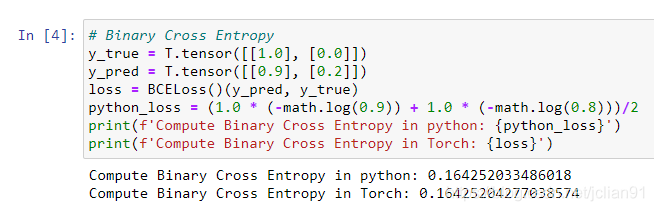
從上面的結(jié)果中可以看到Keras和PyTorch在實(shí)現(xiàn)BCE損失函數(shù)的差異，給定樣本，Keras給出了每個(gè)樣本的BCE，而PyTorch給出了所有樣本BCE的平均值。更大的差異體現(xiàn)在
多分類(lèi)交叉熵?fù)p失函數(shù)。Categorical Cross Entropy
??Categorical Cross Entropy（CCE）為多分類(lèi)交叉熵?fù)p失函數(shù)，是BCE（二分類(lèi)交叉熵?fù)p失函數(shù)）擴(kuò)充至多分類(lèi)情形時(shí)的損失函數(shù)。多分類(lèi)交叉熵?fù)p失函數(shù)的數(shù)學(xué)公式如下：
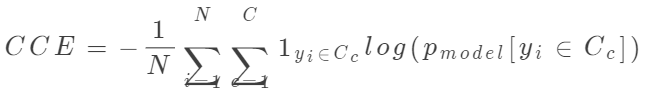
其中N為樣本數(shù)，C為類(lèi)別數(shù)，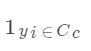
表示第i個(gè)樣本屬于第c個(gè)類(lèi)別的值（0或1），
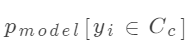表示模型預(yù)測(cè)的第i個(gè)樣本屬于第c個(gè)類(lèi)別的概率值（0-1之間）。如需查看具體的計(jì)算方式，可以參考文章多分類(lèi)問(wèn)題的交叉熵計(jì)算。
??Keras實(shí)現(xiàn)代碼如下：
??PyTorch中的CCE采用稀疏多分類(lèi)交叉熵?fù)p失函數(shù)實(shí)現(xiàn)，因此直接查看稀疏多分類(lèi)交叉熵?fù)p失函數(shù)部分即可。
Sparse Categorical Cross Entropy
??Sparse Categorical Cross Entropy（稀疏多分類(lèi)交叉熵?fù)p失函數(shù)，SCCE）原理上和多分類(lèi)交叉熵?fù)p失函數(shù)（CCE）一致，屬于多分類(lèi)問(wèn)題的損失函數(shù)，不同之處在于多分類(lèi)交叉熵?fù)p失函數(shù)中的真實(shí)樣本值用one-hot向量來(lái)表示，其下標(biāo)i為1，其余為0，表示屬于第i個(gè)類(lèi)別；而稀疏多分類(lèi)交叉熵?fù)p失函數(shù)中真實(shí)樣本直接用數(shù)字i表示，表示屬于第i個(gè)類(lèi)別。
??Keras實(shí)現(xiàn)代碼如下：
例子中一共四個(gè)樣本，它們的真實(shí)樣本標(biāo)簽為[2,2,0,1]，不是one-hot向量。
??PyTorch中的SCCE實(shí)現(xiàn)代碼與上述數(shù)學(xué)公式不太一致，有些微改動(dòng)。我們先看例子如下：
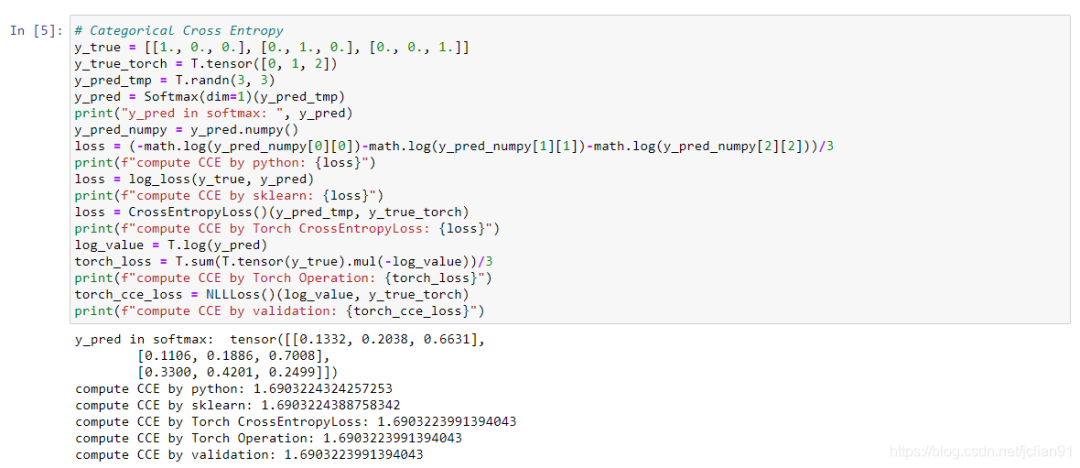
這明顯與Keras實(shí)現(xiàn)代碼是不一致的。要解釋這種差別，我們就要詳細(xì)了解PyTorch是如何實(shí)現(xiàn)CCE損失函數(shù)的。
??簡(jiǎn)單來(lái)說(shuō)，PyTorch中的輸入中的樣本預(yù)測(cè)，不是softmax函數(shù)作用后的預(yù)測(cè)概率，而是softmax函數(shù)作用前的值。對(duì)該值分別用softmax函數(shù)、log函數(shù)、NLLLoss()函數(shù)作用就是PyTorch計(jì)算SCCE的方式。
??在上面的例子中，y_pred_tmp是softmax函數(shù)作用前的值，是PyTorch計(jì)算SCCE的預(yù)測(cè)樣本的輸入，y_pred是softmax函數(shù)作用后的值，是sklearn模塊、Keras計(jì)算SCCE的預(yù)測(cè)樣本的輸入。對(duì)y_pred_tmp、y_true使用softmax函數(shù)、log函數(shù)所得到的結(jié)果，與y_pred、y_true使用sklearn模塊、Keras計(jì)算SCCE的結(jié)果一致，而對(duì)該結(jié)算結(jié)果再作用NLLLoss()，就是PyTorch計(jì)算SCCE的方式。
??也許上面的解釋還有點(diǎn)模糊，我們借助知乎上別人給出的一個(gè)例子也許能更好地理解PyTorch計(jì)算SCCE的方式，代碼如下：
# -*- coding: utf-8 -*-
import torch
import torch.nn as nn
x_input = torch.randn(3, 3) # 隨機(jī)生成輸入
print('x_input:\n', x_input)
y_target = torch.tensor([1, 2, 0]) # 設(shè)置輸出具體值 print('y_target\n',y_target)
# 計(jì)算輸入softmax，此時(shí)可以看到每一行加到一起結(jié)果都是1
softmax_func = nn.Softmax(dim=1)
soft_output = softmax_func(x_input)
print('soft_output:\n', soft_output)
# 在softmax的基礎(chǔ)上取log
log_output = torch.log(soft_output)
print('log_output:\n', log_output)
# 對(duì)比softmax與log的結(jié)合與nn.LogSoftmaxloss(負(fù)對(duì)數(shù)似然損失)的輸出結(jié)果，發(fā)現(xiàn)兩者是一致的。
logsoftmax_func = nn.LogSoftmax(dim=1)
logsoftmax_output = logsoftmax_func(x_input)
print('logsoftmax_output:\n', logsoftmax_output)
# pytorch中關(guān)于NLLLoss的默認(rèn)參數(shù)配置為：reducetion=True、size_average=True
nllloss_func = nn.NLLLoss()
nlloss_output = nllloss_func(logsoftmax_output, y_target)
print('nlloss_output:\n', nlloss_output)
# 直接使用pytorch中的loss_func=nn.CrossEntropyLoss()看與經(jīng)過(guò)NLLLoss的計(jì)算是不是一樣
crossentropyloss = nn.CrossEntropyLoss()
crossentropyloss_output = crossentropyloss(x_input, y_target)
print('crossentropyloss_output:\n', crossentropyloss_output)
輸出結(jié)果如下：
x_input:
tensor([[ 0.1286, 1.1363, 0.5676],
[ 1.0740, -0.7359, -0.6731],
[ 0.7915, -0.8525, -1.2906]])
soft_output:
tensor([[0.1890, 0.5178, 0.2932],
[0.7474, 0.1223, 0.1303],
[0.7588, 0.1466, 0.0946]])
log_output:
tensor([[-1.6659, -0.6582, -1.2269],
[-0.2911, -2.1011, -2.0382],
[-0.2760, -1.9200, -2.3581]])
logsoftmax_output:
tensor([[-1.6659, -0.6582, -1.2269],
[-0.2911, -2.1011, -2.0382],
[-0.2760, -1.9200, -2.3581]])
nlloss_output:
tensor(0.9908)
crossentropyloss_output:
tensor(0.9908)
Hingle Loss
??Hingle Loss為合頁(yè)損失函數(shù)，常用于分類(lèi)問(wèn)題。合頁(yè)損失函數(shù)不僅要分類(lèi)正確，而且確信度足夠高時(shí)損失才是0，也就是說(shuō)，合頁(yè)損失函數(shù)對(duì)學(xué)習(xí)有更高的要求。一個(gè)常見(jiàn)的例子為SVM，其數(shù)學(xué)公式如下：
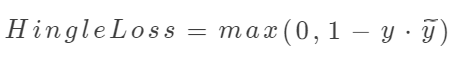
其中為真實(shí)標(biāo)簽，為預(yù)測(cè)標(biāo)簽。
??Keras實(shí)現(xiàn)代碼如下：
??PyTorch中沒(méi)有專門(mén)的Hingle Loss實(shí)現(xiàn)函數(shù)，不過(guò)我們可以很輕松地自己實(shí)現(xiàn)，代碼如下：
總結(jié)
??本文介紹了NLP任務(wù)中一些常見(jiàn)的損失函數(shù)（Loss Function），并使用Keras、PyTorch給出具體例子。
??本文代碼已上傳至Github，地址為：https://github.com/percent4/deep_learning_miscellaneous/tree/master/loss_function 。
??2021年4月24日于上海浦東，此日惠風(fēng)和暢~
參考網(wǎng)址
How To Build Custom Loss Functions In Keras For Any Use Case：https://cnvrg.io/keras-custom-loss-functions/
Pytorch常用的交叉熵?fù)p失函數(shù)CrossEntropyLoss()詳解：https://zhuanlan.zhihu.com/p/98785902